灰色误差理论在地矿的分析与测试数据处理中的应用

（云南省地质矿产勘查开发局中心实验室，云南 昆明 650217）

在传统数据处理过程中，主要是以经典统计学作为理论基础，在样本不确定的情况下采用概率统计方法，要求具有经典分布和大量的测量数据样本，特别是在评估测量不确定度时，相应的计算量相对较大。而且计算过程相对复杂。小样本的数据分析准确性很低。新的统计理论方法的出现，有可能突破基于统计理论的方法。这种新方法已深入应用于机械、计量、航空等领域，即灰色系统理论。模糊理论，贝叶斯推断理论，神经网络建模，间接测量理论等一些非统计学理论。例如，在王忠禹等人的研究中，基于动态测量和精密测量，可以从机械场的测量问题入手，提出一种测量不确定性的非统计理论。由于地矿样本测试过程中存在许多过程，并且影响了许多因素，因此存在许多不确定因素。通常，矿物分析是一种小范围的信息分析。使用它作为标准数量，完成比较过程以进行不完美的测量。

1 理论分析

（1）灰色误差。在实际测试过程中，通常很难获得真实值，并且经常使用要测量的实际值而不是实际值。在满足一定精度的情况下，实际值是真值的无限接近值，在某些条件下是相对增白值，所以我们可以将灰度误差形式定义为E（误差）=E（测量值）-E（真值）。其中，如果在理想条件下没有测量误差，则每次获得的测量结果为其真值，并且可以假设存在n个数据的序列。其中d为真实值，在实际测量中由于存在误差值，导致测试值无限接近真实值但不等于真实值，在该值周围存在一定程度的分散，其可以按升序排列在下面的公式中。

（2）评定标准测量不确定度。对上述公式进行累加能够获得累加序列，如下所示。

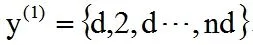
其中累加曲线数呈现直线型，因此其方程为，

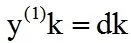
对上述公式进行累加后能够获得累加系列，如下所示。

这种累加曲线为曲线形。由上述公式我们可以发现在理想条件下，真实值和累积值与测量数量成线性关系。我们考虑坐标原点位置在两者之间的距离差，其变化规律由零逐渐增加，最后又逐渐减小。在等精度测量过程中，测量值可以分组为数据列，如下所示。

为进一步消除参考累加直线和测量累加曲线距离的随机性，我们可以根据数据按升序进行排列，将获得数据序列和测量累加曲线。

（3）粗大误差判定。对于其他误差，测量值累积曲线可以在判断过程中由折线包围。由于在测量数据中值是最大距离值，还可以使用测量数量的中值作为包络折线的转折点。考虑到数据有一定的变化，可以将最大距离增加h倍，然后多次测量点，并将距离增加到h次，以便能够转动转折点。测量累积数据的上限和下限。最终累积曲线包含由折线形成的灰色区域，应当剔除该数据。

2 应用案例分析

我们可以基于灰色系统理论，将随机量作为一定范围内的变化灰色数，将这种过程看做是某一范围，某一时间段内变化的灰色过程，同时认为客观系统数据杂乱，但整体上是有规律性的，通过对原数据进行处理发现其规律性，进而对该设计变化做出描述，生成使灰过程变白的一种重要方法，存在累加和累减生成的数据处理方式，通过生成处理数据之后，能够弱化原有的随机性，使原始数据更具有规律性排列。地矿测试实际上就是在寻求某一条件下哪个更接近于真值，减少误差，寻求最接近真值的相对白化值，因此可以在地矿数据处理中运用灰色误差理论。地矿测试的数据中包含了物理、化学定量定性分析数据。从定量数据上来看，利用传统统计方法是以大量数据和服从正态分布作为前提的，在实际工作中所研究的数据往往只设计一到多个，很难达到大数据测量要求。在特殊情况下对于一些不均匀的地矿数据来说，有一些分散性大块状矿物的力学强度数据分散大，测量次数有限。虽然利用传统数据能够进行数据分析，但这些数据往往存在一定的特殊性，很难利用现有的误差理论进行判断。在本研究中基于等精度测量条件下选择有标准值的铜矿石标准物质进行地矿分析，以及无标准值的其它矿物的抗压强度数据，采用同一样品增加检测次数，存在不均匀性明金分布的样品中检测金含量以及某矿样在不同碎样粒度下金检测数据进行比较，同时将这些相关指标与传统统计方法进行比较时，进一步讨论灰色误差理论的应用效果。

表1 实验判断误差表

在数据处理过程中，由于灰度误差理论和应用范围的要求，为了减小参考累积线和测量累积曲线的距离随机性，我们按升序累加原始数据，然后在获得数据列后累积生成的数据。比如在进行粗大误差判断过程中，对某矿样处于不同碎样粒度条件下完成金检测。通过九次实验判断总误差，使用Legend的传统方法，Grobs准则和Romanov准则，结果如下。

其中数列1中（2.02 2.24 1.36 1.37 2.60 2.62 2.81 2.90）平均值为2.51，相对标准差为0.2822数列2中（2.15 2.23 2.44 2.63 2.68 2.71 2.71 2.86 3.10）平均值为2.61，相对标准差为0.2985。

根据数据1的结果发现，碎样粒度平均值为2.51，相对偏标准偏差为0.2822，测量次数为9，包络线转折点p等于五，由测量数据可以发现两直线间的距离为1.04，怀疑所测得的数据值X1为2.02，x9为2.90，有可能存在粗大误差。根据结果发现测量值不含粗大误差，是与传统方法检测结果一致的。

3 结语

本文深入阐述了灰色误差理论的研究成果，并将其运用于地矿测试处理中，能够获得满意的测试效果。具体来看，在矿石和矿物的化学分析过程中数据的累积曲线对于误差的小变化范围具有线性关系。其数据测量的累积曲线呈现曲线关系。然而传统统计标准偏差是与灰色标准偏差十分接近的，利用这种方法能够获取较高精度和实用性。