基于R/S分析的阿坝藏族羌族自治州年降雨量定量预测
陈江峰,龚书浩,李迎超
(1.河南理工大学 资源环境学院,河南 焦作 454003;2.河南省核工业放射性核素检测中心, 河南 郑州 450044; 3.黄河交通学院,河南 武陟 454950)
降雨量是水循环过程中最重要、最活跃的因素之一,降雨量的分布会直接影响到径流等水文环境,同时降雨量也是描述一个地区气候变化的关键指标,一个地区降雨量的多少对当地气候环境、水资源分布、生态系统等都会产生重要影响。由于降雨等自然现象具有突发性,在发生时间上存在不规则性,降雨量的大小又受多种复杂因素的影响,因此很难对降雨量进行精准预测。近年来,国内外研究人员发现,看似无序、不规则的降雨现象实际并不是完全随机的,而是蕴含着规律,比如自相似性,这是传统理论难以解释的,因此越来越多的学者开始利用分形几何学等理论来探讨降雨现象的发生规律。
Hurst提出的重标度极差法(R/S分析法)是分析时间序列的有力工具,是分形理论的重要方法之一[1],其优势在于无论时间序列是正态分布还是非正态分布,分析结果的稳定性均不受影响,因此迄今仍然是估计Hurst指数时最常用的方法[2]。R/S分析法以其能够描述非线性时间序列复杂变化内在规律的特点,在水文学和气象学研究中有着广泛应用[3-4]。目前利用R/S分析法研究时间序列取得了很大进展,但这类方法的研究与应用对象均是时间序列的趋势性分析,属于定性预测。本研究在R/S趋势性分析研究的基础上,考虑时间序列长度和相关性等因素,辅以计算机技术,实现了降雨量的定量预测。
1 理论基础
1.1 β-Z-H三参数综合趋势分析
1.1.1 Mann-Kendall检验
Mann-Kendall(M-K)检验法是一种非参数统计检验法,广泛适用于非正态分布特征变量的趋势分析。设x1,x2,…,xn为时间序列数据,n为时间序列数据的长度,对于所有t、τ≤n,且t≠τ,xt和xτ的分布是不同的,M-K法定义统计量S为
(1)
其中
式中:xt、xτ分别为序号t、τ对应的时间序列数据。
S的方差Var(S)计算公式为
Var(S)=[n(n-1)(2n+5)-
(2)
式中:i为时间序列数据出现的次数;ei为时间序列数据出现次数的个数。
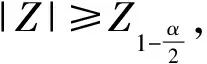
(3)
在M-K检验中,另一个非常有用的指数为肯德尔斜率β,它表示时间序列趋势大小,若β>0,则为上升趋势,若β<0,则为下降趋势,若β=0,则说明趋势不明显[6]。β值计算公式为
(4)
1.1.2 Hurst指数
R/S分析的基本思想是改变样本序列的时间尺度,研究其在不同尺度范围内的统计规律,从而进行大小时间尺度间的相互转换[7-8]。该方法能从分形时间序列中区分出随机和非随机序列。通过Hurst指数的判定,可以判断出时间序列的分形结构和状态持续性,为时序的复杂性演变提供一种有效的非线性科学预测方法[9]。
对于一个随机过程样本序列,如果其物理量的时间序列为x1,x2,…,xn,满足
(5)
式中:τ为时间序列的序数;R(τ)为时间序列对应的累积偏差的域;S(τ)为R(τ)对应的标准偏差;R(τ)/S(τ)为重标极差;H为Hurst指数,其值介于0到1之间[10],可以在双对数坐标系中根据[lnτ,ln(R/S)]的值用最小二乘法拟合求得。
若H=0.5,则表明现在和未来之间没有相关性;若0 对一个具有状态持续性的时间序列来说,具有长记忆效应特征。从理论上讲,今天所发生的一切将一直影响未来,即存在对初始条件的敏感性[12],对时间序列做Vτ~lnτ分析,即 (6) 此时Vτ图像对应τ的循环变化长度是时间序列持续性的平均长度,是统计意义上的数值,而非时间序列的真正周期,也是预测初始序列长度选取的可行值[13]。当图中有多个拐点时,遵循最大H值且拟合度较高的原则选择突变点作为循环长度的平均值[13]。 H值反映了时间序列的趋势性,若0 (1)对时间序列进行R/S趋势性分析,得到线性回归方程ln(R/S)=a0lnτ+a1,将ln(τ+1)代入线性回归方程,得到回归方程下一点的最优值ybest。 (2)将假设数据x(τ+1)作为下一点的新数据代入相关计算机程序中进行运算,得到新的预测点值ln(R/S)τ+1,判断|ln(R/S)τ+1-ybest|<Δt是否成立(Δt可以根据需求赋值,以误差最小、预测精度最高为准则)。如成立,则此时的x(τ+1)即为定量预测点,程序停止运行,输出x(τ+1),否则进行下一步。 (3)若上步不满足,则程序再次改变迭代数据,通过连续运算输出满足要求的原始数据,即为误差范围内距离ybest最近的原始数据,即为下一点的定量预测值x(τ+1)。 阿坝藏族羌族自治州地处青藏高原东南缘、横断山脉北端与川西北高山峡谷的接合部,气温分布自东南向西北随海拔升高而降低:海拔2 500 m以下的河谷地带降水集中、蒸发快,为干旱、半干旱地带;海拔2 500~4 100 m的坡谷地带为寒温带,年平均气温1~5 ℃;海拔4 100 m以上为寒带,终年积雪,长冬无夏。本研究采用阿坝州小金水文观测站实测年降雨量数据(1961—2000年)进行分析和预测(图1)。 图1 阿坝州年降雨量变化曲线 对年降雨量数据进行R/S趋势性分析,得到H=0.663 1、R2=0.945 2,表明该时间序列具有正持续性,时间序列在未来的增减性与原来是相同的,但持续性较弱,如图2所示。 将年降雨量数据带入M-K检验公式(1)~(4)中得到Z=0.338,β=1.532。β是评价时间序列历史发展趋势的指标,Z可以反映其显著程度,H能反映时间序列未来发展的持续性。β、Z、H都是对时间序列进行分析的指标,进一步将三者综合,则不同的数值对应关系 图2 年降雨量R/S趋势预测 具有不同的指示意义。在α=0.05置信水平上,β-Z-H三参数综合分析对降雨演化特征的指示作用如表1所示。 表1 β、Z、H综合分析的指示作用 根据之前得出的Z=0.338,β=1.532,H=0.663 1,结合β、Z、H综合分析指示作用表分析知,研究区年降雨量时间序列符合序号7的特征,即降雨量过去是增加的,未来将持续增加,但是趋势不明显,这与R/S趋势分析得到的结果是相同的。 如果初始序列长度过大,数据的波动性将会增强,回归方程的线性关系就会减弱,因此选取合适的初始序列长度对预测结果的准确性尤为重要。对上述时间序列做Vτ~lnτ分析(图3),时间序列循环变化长度为12,因此选取12为时间序列预测的初始长度。 图3 降雨量时间序列长记忆性分析 记1982—1993年降雨量数据为序列A,以后新的序列依次命名为序列B、C等。对该时间序列进行R/S分析,得到回归方程如图4所示,H=0.548 17,R2=0.977,那么R/S趋势预测点之间存在良好的线性关系,可以尝试对该时间序列进行定量预测,得到的预测值x(13) 为628 mm。 图4 序列A的 R/S定量预测 将x(13)放入序列A中得到序列B,对序列B进行同样运算,得到预测值x(14)=637 mm(图5)。同理,得到序列C(图6),预测值x(15)=636 mm。 图5 序列B的R/S定量预测 图6 序列C的R/S定量预测 对得到的预测值与真实降雨量进行精度检验,结果见表2。 表2 初始序列长度为12的定量预测值与真实值对比 将预测值与真实值对比可以看出,初次预测和第二次预测结果较为理想,特别是第一次预测精度为97.6%,但是第三次较前两次误差增大,说明随着预测时间序列长度的增加,时间序列的波动性增强,内在规律性减弱。总体而言,模型预测的平均相对残差为7.1%,平均预测精度为92.9%,预测效果显著。 (1)辅以计算机技术,实现了R/S分析方法的定量预测,将非线性时间序列问题进行了线性求解,将该模型应用于降雨量预测,平均精度高达92.9%。 (2)R/S定量预测与初始序列长度有关,连续多次预测会使模型精度有所降低,因此对时间序列长度的选择进行分析,显得尤为重要。 (3)随着人类活动的日益增强,降雨量大小预测变得更为复杂,运用R/S分析对降雨量进行定量预测,可为非线性时间序列问题的解决提供一种快速而有效的方法。1.2 初始序列长度
1.3 R/S定量预测方法的基本原理
2 R/S定量预测实例
2.1 数据来源
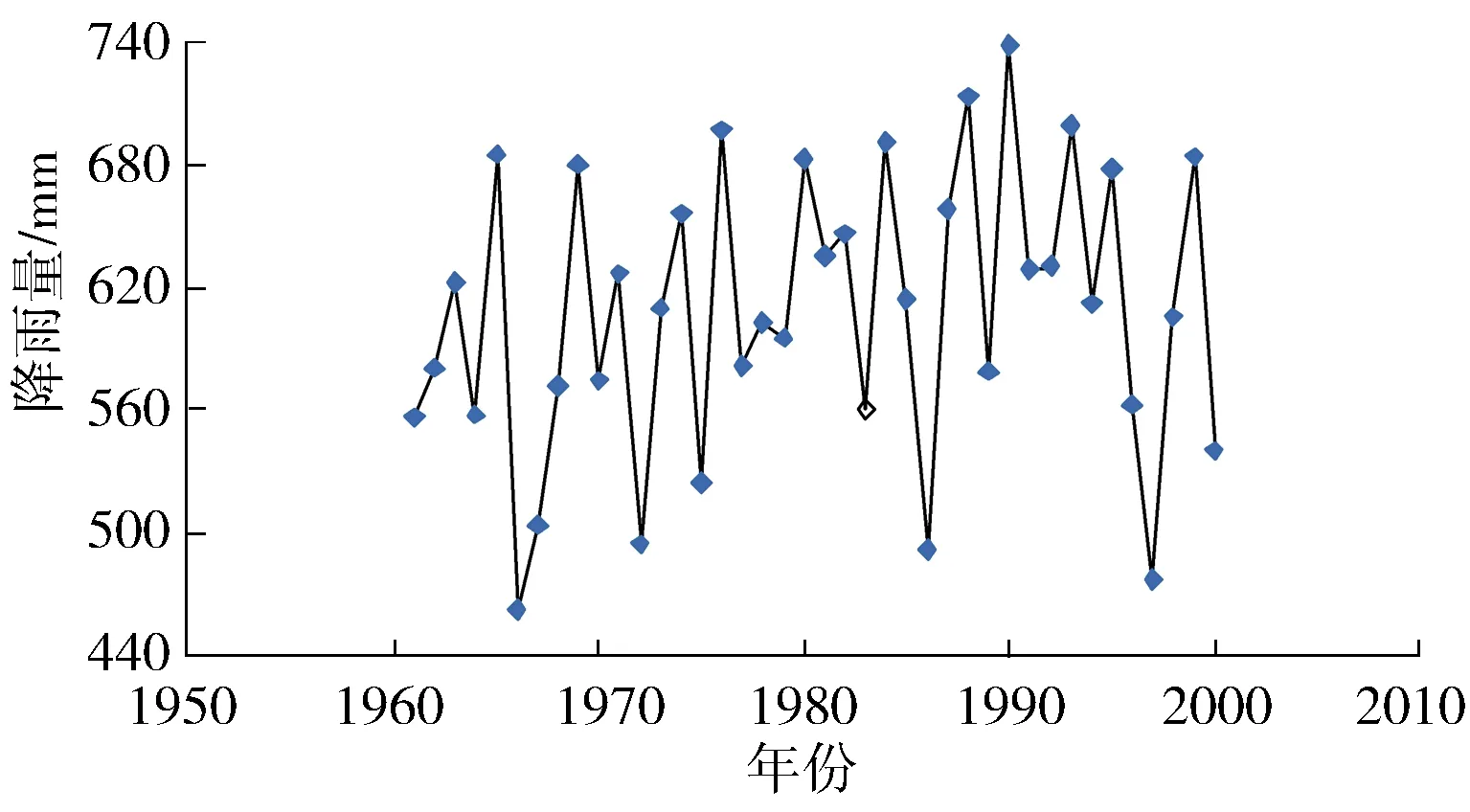
2.2 年降雨量β-Z-H三参数综合趋势分析
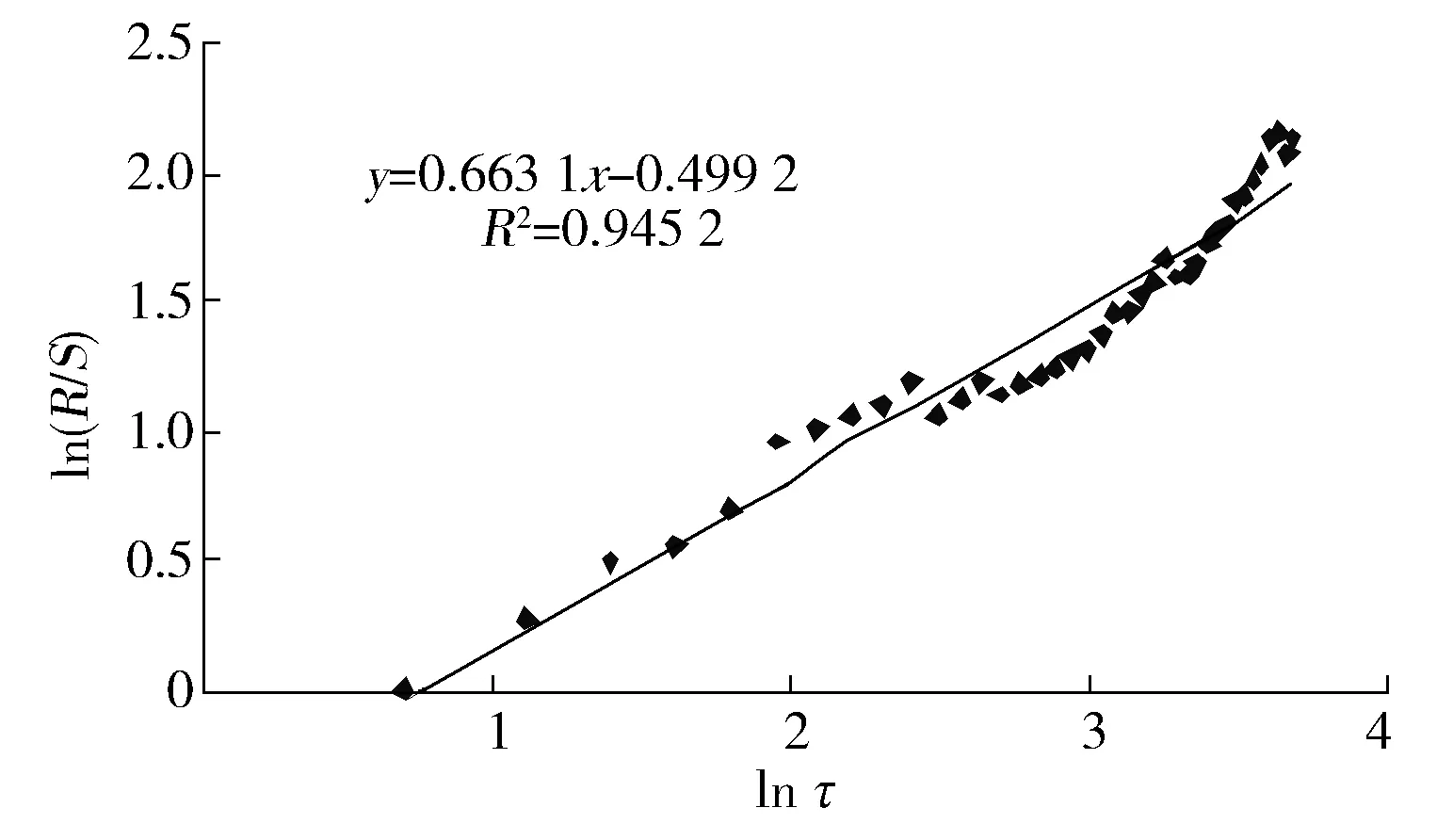
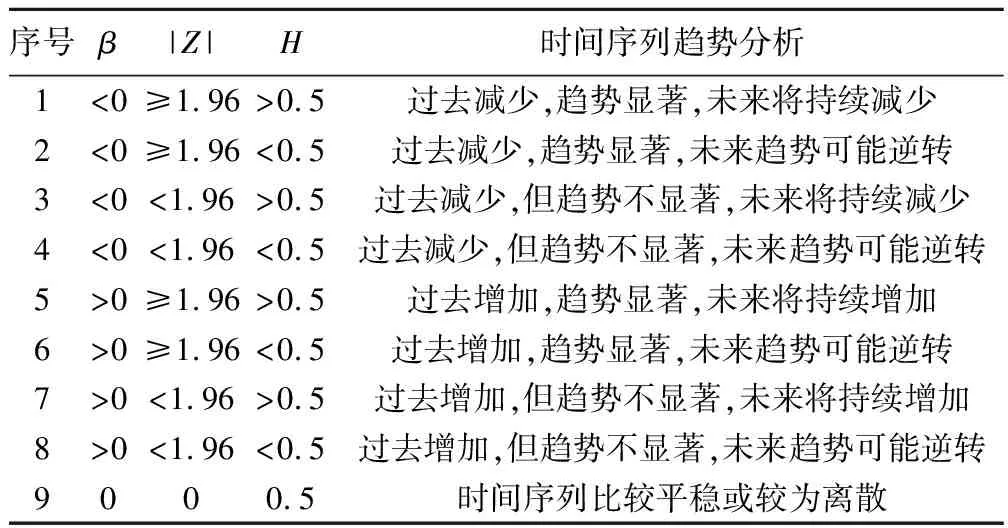
2.3 初始序列长度
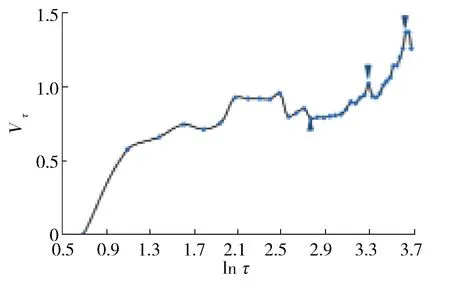
2.4 R/S定量预测
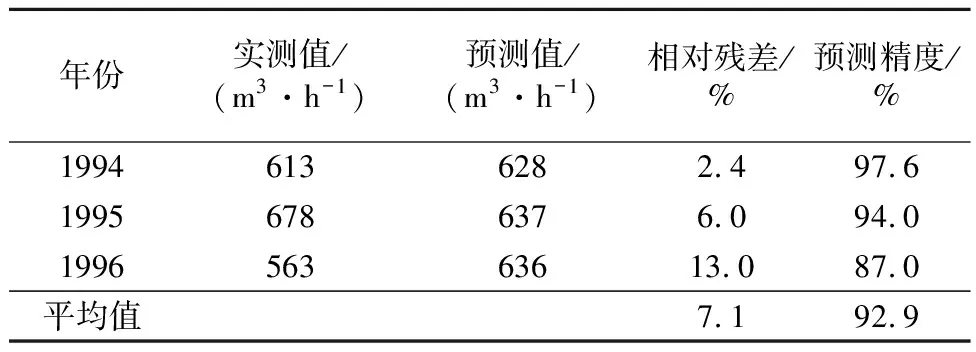
2.5 预测精度检验
3 结 论

