室内土遗址气-液相变补水的可行性研究
——以杭州萧山跨湖桥遗址博物馆为例
王思嘉,张秉坚,2,吴 健
(1. 浙江大学文博系,浙江杭州 310028; 2. 浙江大学化学系,浙江杭州 310027; 3. 杭州萧山跨湖桥遗址博物馆,浙江杭州 311203)
0 引 言
土遗址的保护一直是比较困难的课题。在遗址博物馆中,室内土遗址病害的基本原因是水分不断从土体向上单向迁移和蒸发。由此引发可溶盐的向外迁移、表层粉化、土体开裂等一系列病害[1-4]。在过去的一二十年中,保护工作者已经尝试使用多种化学材料进行加固,但是只要水分的单向迁移和蒸发不断,表层剥离等保护性破坏现象就会发生[1]。
前期调研表明,恒定含水量是土遗址保持稳定的必要条件[1]。因此,提出一种新的土遗址保护理念:维持水分的平衡,即设法使土体内的水分保持基本不变。这样盐分就不会迁移和析出结晶、土块也不会干缩形成裂隙。对于室内土遗址意味着需要“适量补水”,以稳定土中的盐分、防止土体开裂和粉化。适量补水需要解决两项关键技术,其一是如何补水;其二是如何达到恰当的水量。这里,第一项技术是基础。在补水技术方面,喷洒(喷淋、喷雾等)是最简单的方法,但是长期的喷洒无疑会使土体表面板结,从而改变遗址原貌。作为一种尝试,本课题组开展了补水于无形的“气-液相变补水”的探索性研究。
存在于自然界的水有固态、液态和气态三种状态。在一定温度和蒸汽压下水的状态会发生改变,这种变化即为“相变”[5],一般将水由气态变为液态的过程称为凝结或冷凝。气态水在土壤表面和孔隙中凝结是均匀增加土壤湿度的最佳方式,如果能利用该凝结过程使遗址土体的含水率增高,使盐分溶解并渗透至深处,这无疑是一种具有创新意义的土遗址保护措施。
实际上“气-液相变补水”是普遍存在的自然界现象。例如,非降雨形成的液态水是土壤和植被获取水分的重要方式。在极端干旱的环境中,露水的量可以超过降雨量,甚至是植物获取液态水的唯一来源。国内外的农学家、气象学家、土壤学家等已经开始关注土壤冷凝水这一研究领域,他们揭示了这一现象的物理原理,并不断寻找预测方法,以期对这一现象进行利用。目前国内外对于土壤吸湿的研究基本上都是通过建立物理模型进行计算,然后现场实验测量冷凝水量,以验证计算结果的可靠性[6-7]。孟繁华等[8]利用土柱模拟试验发现影响土壤冷凝水的因素有昼夜温差和潜水埋深等。李小刚等[9]研究了土壤吸附水与盐分之间的关系,发现盐分显著增加了土壤水汽吸附量。但是由于土壤冷凝过程非常复杂,这一预测过程存在很多变量,目前国际上尚无比较可行的土壤冷凝水的预测方法,特别是以建立人工气-液相变补水环境为手段,达到土壤可控润湿为目标的研究还未见于报道。
对于封闭的平衡体系,由水的饱和蒸汽压公式、空气的湿度、空气和固体表面的温度差,就能预测冷凝现象是否会发生,并可计算出冷凝水量。但是对于实际土遗址,由于:1)土壤矿物颗粒性质的不同;2)土体结构和孔隙的差异;3)空气温湿度、土体温度和含水率的非均匀性;4)水在气-液相间传质速率的影响;5)土壤中可溶盐溶解后引起的水蒸汽压降低。这些物理因素和非平衡过程使得理论预测变得十分困难。为了利用水汽自动在土壤中凝结的规律,以达到“气-液相变补水”的目标,本工作以杭州萧山跨湖桥遗址博物馆土遗址为例进行了试验研究、凝水量预测和现场实验研究。
1 土壤水汽凝结小试验
一般情况下,土壤中水量平衡方程式为:
P+I+C=E+D+ΔW
(1)
式中:P为有效降水量;I为灌水量;C为气态水凝结量;E为土壤蒸发量;D为排水或渗透量;ΔW为某时段内土壤含水量W的变化量。针对室内土遗址,可以忽略P、I;本试验以带底容器装载土样,可认为D=0。土壤水量平衡方程为:ΔW=C-E。试验在高湿条件下进行,忽略E,可用电子天平直接获得ΔW。
1.1 试验装置
自建试验装置如图1所示,a为直径5 cm培养皿,以盛装土样;b为外径7.5 cm、高5 cm的夹层烧杯,以通冷却水维持土样温度;c为内径30 cm的带出口孔塞的真空干燥器,下层放置KNO3或KCl饱和溶液以维持干燥器内湿度;所有需要隔温处用聚氨酯发泡剂和铝膜玻纤布胶带包裹。

图1 气-液相变补水试验装置图Fig.1 Small test device of gas-liquid phase transition experiment
整个试验装置放入恒温烘箱中以控制环境温度;夹层烧杯中的冷却水通过橡胶管由低温恒温槽提供。这里,盛装土样的培养皿需要特别注意防止壁面直接暴露在空气中,不仅需要使用聚氨酯发泡剂对培养皿内外壁进行包敷,同时需要对培养皿上沿口边缘切割,使发泡保温套边缘向外侧倾斜,避免容器边缘的冷凝水流入容器。
1.2 土壤样品
萧山跨湖桥遗址博物馆土遗址现场典型析盐的XRD分析结果见图2。

图2 萧山跨湖桥遗址博物馆土遗址典型析盐的XRD分析结果Fig.2 XRD analysis results of typical salts of the earthen site of Kuahuqiao Site Museum in Xiaoshan
将从遗址博物馆取来的土样置于通风处晾干,除去杂质,用自来水反复浸泡至上层清液的电导率接近自来水电导率时停止换水。将土样在105 ℃下烘至恒重,用研钵将块状土捣碎过200目筛,使土样保持松散状态。
1.3 控制条件
设计3个控制条件:
1) 空气温度与土壤表面温度差ΔT。通过分别控制恒温烘箱和低温恒温槽温度,可以得到空气温度与土壤表面温度的差值。该装置能制造的三个温度差值如表1所示。

表1 试验中空气温度与土壤表面温度的差值表Table 1 Difference between air temperature and soil surface temperature (℃)
2) 空气湿度RH。通过在真空干燥器底层放置KNO3、KCl或不放盐来控制空气湿度,试验中饱和KNO3、KCl和纯水在30~36 ℃时的空气湿度RH测量值见表2。
3) 可溶盐含量S。将已经过脱盐的土壤样品分别补充一定量的Na2SO4,使其含盐量为1.223、12.23、24.46 g/kg,来模拟三种不同含盐量的土壤样品。
1.4 试验步骤
1) 开启恒温烘箱和低温恒温槽,设置试验所需温度,预热干燥器,制造高温高湿环境,直至干燥器内的温度和湿度稳定。
2) 准确称取土样20 g,精确至0.001 g,倒入培养皿,使土壤表面平整,置于干燥器内的夹层烧杯上。
3) 2 h后关闭烘箱并记录温度和湿度。迅速取出培养皿,用红外测温仪测量土表温度。
4) 将容器置于天平上,记录数据后进行拍照,放回干燥器内并再次开启烘箱。直至样品增重大于等于4 g时,结束试验。
1.5 试验轮数和冷凝水量计算
若考虑3个控制条件:ΔT、RH和S,和3个水平,共需进行了27轮试验。预备试验发现,当RH小于60%,ΔT小于15 ℃时试验无法正常进行。此时水在土壤上的冷凝现象非常微弱,这使试验时间拉长,试验误差增大。因此去掉6个难以进行的试验,试验共计进行21轮。
在全部试验结束以后,对试验所得的数据进行处理。认定样品在试验时间内增加的质量为气相水在样品中凝结成液态水的质量,用该质量除以培养皿土样的面积,以求得单位样品面积的冷凝水量w(kg·m-2),即由下式计算:
(2)
式中,m0为土壤样品与培养皿初始总质量,mi为第i轮气-液相变补水试验结束后土壤样品与培养皿的总质量,r为培养皿的半径,本试验中r=0.0 025 m。
1.6 小试验现象和结果
1) 土壤样品冷凝过程状况。在对土样进行气-液相变补水试验过程中,土样表面润湿状况见图3。
由图3可明显发现,含盐量多的土壤在试验过程中表面润湿现象发生较早,土壤表面首先出现点状润湿,随后润湿点越来越密集,最后形成面状润湿。含盐量极低的土在试验过程中表面润湿现象发生较晚,至12 h后才出现,主要表现是面状润湿。
2) 土壤样品冷凝量。不同控制条件下,土壤样品冷凝水量与试验时间的关系可绘成折线图表示。
(1) 不同空气湿度RH对土样冷凝量的影响如图4所示。由图4可知,单位时间内环境中空气湿度越大,土样的冷凝水量越大。

图4 含盐量S和温差相同时,不同空气湿度对土样冷凝量的影响Fig.4 Effect of different air humidity on soil sample condensation with the same salt content and temperature difference
(2) 不同温差ΔT对对土样冷凝量的影响如图5所示。由图5可知,单位时间内,当空气温度高于土壤表面时,空气与土壤表面之间的温差越大,土样冷凝水量越大。
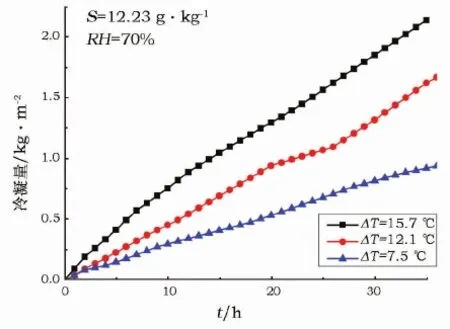
图5 空气湿度和土体含盐量相同时,不同温差对土样冷凝量的影响Fig.5 Effect of different temperature difference on soil sample condensation with the same salt content and air humidity
3) 土壤中含盐量S对土样冷凝量的影响如图6所示。由图6可知,环境条件相同时,单位时间内土样含盐量越大,土样冷凝水量越大。
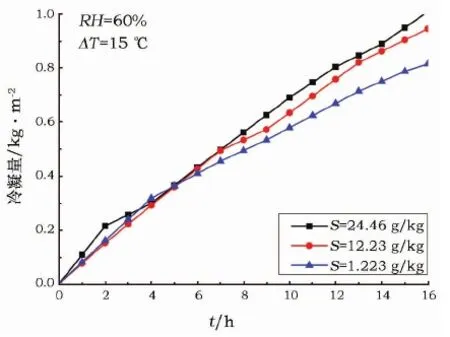
图6 空气湿度和温差相同时,土壤含盐量对土样冷凝量的影响Fig.6 Effect of different salt content on soil sample condensation with the same temperature difference and air humidity
1.7 试验数据关联
在图4~6中,所有土样冷凝量折线都接近直线,表明样品冷凝量与图中的变量之间存在着简单的一元线性函数关系,同时都基本上是从零点开始。因此,冷凝量折线的斜率就是相应条件下土样的冷凝速率z。经过21轮试验,求得不同盐含量S(g·kg-1)、空气湿度RH(%)、空气与土样温差ΔT(℃)的水汽冷凝速率值z(kg·m-2·h-1)如表3所示。
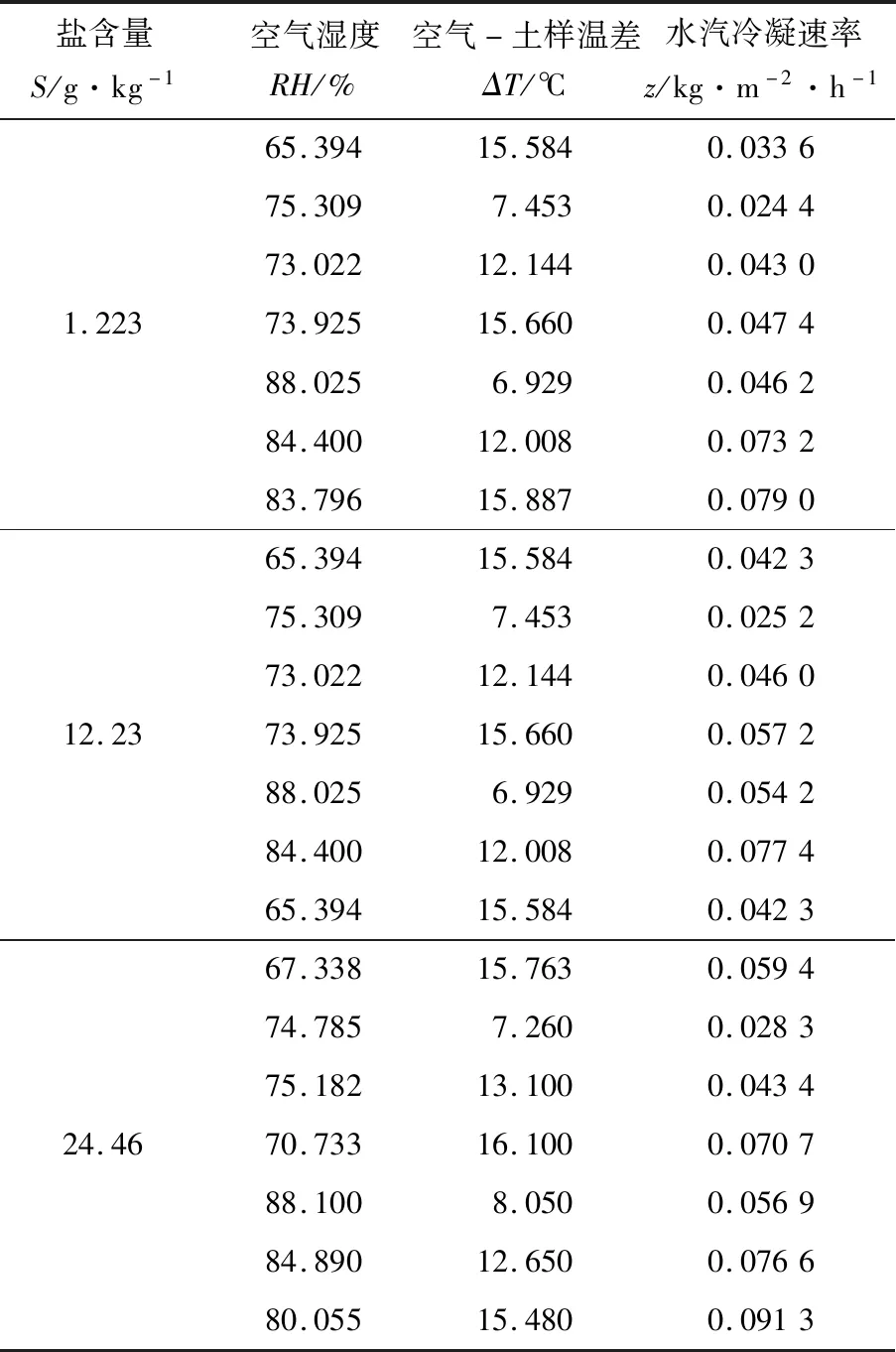
表3 气-液相变补水条件对应的水冷凝速率Table 3 Water condensation rate under each condition
表3中,每个含盐量S下有7轮试验。将RH,ΔT,S分别作为三维空间中的坐标值,发现这7个点的空间分布具有一定规律,利用matlab软件及拟合曲面程序,可以得到以RH和ΔT为自变量的计算水汽冷凝速率z的二元二次方程:
z=f(RH,ΔT)=p00+p10*RH+p01*ΔT+
p20*RH^2+p11*RH*ΔT+p02*ΔT^2
(3)
方程(3)的系数为含盐量S的函数,其中:
1) 含盐量为1.223 g·kg-1的土壤样品的曲面方程系数为:
p00=0.468 p10=-0.013 7
p01=0.001 043 p20=8.858e-5
p11=0.000 191 p02=-0.000 527 7
该方程的三维曲面图如图7所示。
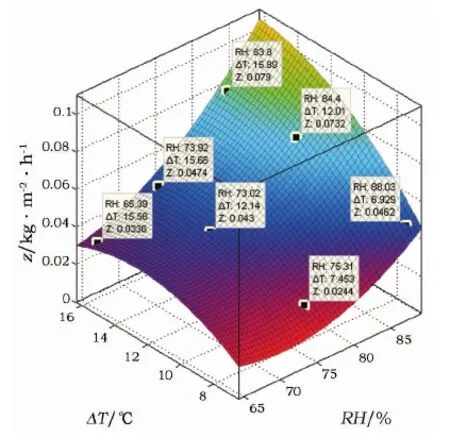
图7 含盐量1.223 g·kg-1土壤样品水汽冷凝速率的三维曲面图Fig.7 Three dimensional surface graph of the condensation rate of soil samples with salt content of 1.223 g·kg-1
2) 含盐量为12.23 g·kg-1的土壤样品的曲面方程系数为:
p00=0.651 5 p10=-0.017 57
p01=-0.008 157 p20=0.000 113
p11=0.000 228 9 p02=-0.000 203 4
该方程的三维曲面图如图8所示。

图8 含盐量12.23 g·kg-1土壤样品水汽冷凝速率三维曲面图Fig.8 Three dimensional surface graph of the condensation rate of soil samples with salt content of 12.23 g·kg-1
3) 含盐量为24.46 g·kg-1的土壤样品的曲面方程系数为:
p00=1.213 p10=-0.026 75
p01=-0.046 45 p20=0.000 160 5
p11=0.000 367 9 p02=0.001 058
该方程的三维曲面图如图9所示。
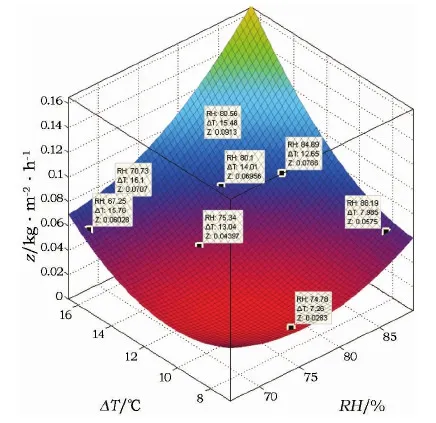
图9 含盐量24.46 g·kg-1土壤样品水汽冷凝速率三维曲面图Fig.9 Three dimensional surface graph of the condensation rate of soil samples with salt content of 24.46 g·kg-1
方程(3)中,每个系数的值都与含盐量S有关,各系数与含盐量S按一元二次方程拟合以后,可以求得每个系数与含盐量S的函数关系:
p00=0.001 3S2-0.000 3S+0.466 4;
p10=-2e-5S2-0.000 1S-0.013 5;
p01=-e-4S2+0.000 5S+0.000 6;
p20=7e-8S2+e-6S+9e-5;
p11=3e-7S2-e-6S+0.000 2;
p02=3e-6S2-e-5S-0.000 5;
将以上关系式代入(3)式,最后得到水汽冷凝速率z对于空气-土壤温差ΔT、空气湿度RH、土壤含盐量S的关联方程:
z=f(RH,ΔT,S)=0.001 3S2-0.000 3S+
0.466 4+(-2e-5S2-0.000 1S-0.013 5)*
RH+(-e-4S2+0.000 5S+0.000 6)*ΔT+
(7e-8S2+e-6S+9e-5)*RH^2+
(3e-7S2-e-6S+0.000 2)*RH*ΔT+
(3e-6S2-e-5S-0.000 5)*ΔT^2
(4)
水汽冷凝速率方程(4)是四维曲面方程,无法用三维坐标图表示。利用该方程可以预测土壤含盐量0≤S≤25 g/kg、空气湿度60≤RH≤95、空气-土壤温差7 ℃≤ΔT≤20 ℃时,气相水在土壤中的冷凝速率z(kg·m-2·h-1)。该方程可为跨湖桥遗址现场试验和未来应用提供补水量预测数据,对于同类土壤的室内遗址也有参考作用。
2 室内土遗址现场气-液相变补水实验
为了考察气-液相变补水方法的可行性,在完成试验和水汽冷凝速率方程的基础上,于2017年1~3月在萧山跨湖桥遗址博物馆进行了现场实验。现场实验在遗址大厅内遗址土壤上进行。
2.1 实验装置
设备:0.5 m×0.5 m×0.5 m的无底薄壁木箱,电热膜,温控开关,水浴锅,小风扇,德图174-H温湿度记录仪,红外测温仪,电子秤(最大量程10 kg),荷兰式取土钻,HSTL-TRSC02型土壤温湿度自动测试仪。
本实验以水浴锅中蒸发的水蒸汽作为气相水源,对遗址表面进行补水。为防止水蒸汽在木箱内冷凝成液态水造成实验误差,因此在木箱内贴电热膜并将其温度设定为高于露点温度。使用温湿度记录仪实时记录箱内的温湿度。设备实物图与原理图如图10所示。

图10 气-液相变补水现场实验装置与原理示意图Fig.10 Device diagram and schematic diagram of the field experiment
2.2 实验条件和步骤
为了达到气-液相变补水的目标,根据现场土壤和空气状况、以及土壤含盐量估算,需要控制实验箱内空气湿度大于80%、空气-土壤温差在15 ℃以上。经过预试验发现,将电热膜温度定在45 ℃,水浴锅温度定在50~55 ℃,24 h可以达到要求。
第一次实验步骤:
1) 将无底薄壁木箱四边埋入遗址区土壤中,将温湿度仪放置在实验区四角。
2) 在水浴锅内加入适量蒸馏水后,用电子秤记录此时水浴锅的质量。
3) 将水浴锅和小风扇置于木箱内,接通电热膜、水浴锅和小风扇电源。设置电热膜温度为45 ℃,水浴锅温度为50 ℃,用红外测温仪测量此时箱内地面土壤温度,并拍照。最后将顶盖盖严。
4) 每隔6 h开盖,快速测量箱内地面土壤温度,并拍照。
5) 24 h后停止实验,并将水浴锅取出称重,减量法计算得到该时间段内进入土体的冷凝水总量。
6) 使用荷兰式取土钻在木箱区地面中央和木箱外距离木箱20 cm处地面分别取深度15 cm的土柱。以每5 cm为单位长度将土柱快速密封,带回实验室进行含水率测试。
第一次现场实验基本达到了气-液相变补水的目标。从数据记录发现,木箱壁面45 ℃电热膜能有效防止水汽在木箱壁面凝结,但连续24 h的电加热也提高了木箱内土壤表面的温度,影响后期补水效果。
第二次实验的步骤和总补水实验时间与第一次相同,改进之处有:
1) 每隔6 h,增加1 h冷却时间。
2) 实验过程中增加土壤温湿度自动测试仪,以了解土壤内部的温度与含水率。
3) 在第14 h后提高水浴锅温度至55 ℃,以提高木箱内的湿度。
2.3 实验结果与讨论
1) 补水量。两次实验的气-液相变补水时间均为24 h。第一次补水量为0.895 kg,第二次实验补水量为0.710 kg。
2) 空气温度和湿度。将温湿度自动测试仪的数据导出后得到两次现场实验的环境温湿度变化曲线如图11所示。

图11 两次实验的空气温湿度变化Fig.11 Changes of air temperature and humidity in the two experiments
由图11可知,除去因人为因素引起的数据波动,在第一次实验中空气最高温度44.4 ℃,最低温度40.7 ℃,平均温度43.1 ℃;最高湿度96.6%,最低湿度80.4%,平均湿度为90.1%。空气温度和湿度的变化波动较小。在第二次实验中,空气的最高温度为44.8 ℃,最低温度41.6 ℃,平均温度44.0 ℃;最高湿度99.4%,最低湿度84.6%,平均湿度为90.0%。空气温度和湿度的波动较大。
3) 土壤表面温度。两次实验土壤表面温度情况如图12上层所示。

图12 土壤表面与内部温度、含水率变化折线统计图Fig.12 Changes of soil temperature and moisture content in the two experiments
由图12左侧上层土壤表面温度曲线可以看到,第一次实验时随着实验进行土壤表面温度不断增高,在第24 h时接近空气温度。由图12右侧上层土壤表面温度曲线可以发现,第二次实验时由于增加了冷却步骤,土壤表面温度出现较大幅度波动,最低温度为19.3 ℃,最高温度为39.6 ℃。
4) 土壤内部温度。由于第二次实验中增加了土壤温湿度自动测试仪,由图12右侧上层土壤3 cm和5 cm处的土壤温度可以看到,前6 h土壤温度明显增加,以后逐渐趋于平稳。
5) 含水率变化。两次实验中用荷兰式取土钻钻取现场土壤深度0~5 cm处的含水率变化情况如图12下层所示,两次实验分别使土壤含水率增加2.203%和4.618%。同样,由土壤温湿度自动测试仪获得的土壤含水率,从深度3 cm到5 cm处都是呈递增趋势。
6) 土壤表面形貌变化。土壤表面形貌变化如图13所示。

图13 气-液相变补水现场实验土壤表面状况Fig.13 Soil surface condition in field experiment
第一次实验进行前,土壤表面白色盐结晶体散布于地面;实验进行12 h后,盐结晶完全溶解并渗入土壤中,土壤被润湿导致颜色变深;24 h后土壤已被整体润湿。实验结束72 h后,仅发现少量白色晶体从土中析出,但远少于实验开始时的数量。第二次实验由于增加了3 h的冷却过程,土壤表面润湿和白色盐结晶的消失要慢一些,直至第24 h土壤才完全润湿;实验结束72 h后,在土壤表面发现有少量白色晶体呈团簇状从土中析出。
7) 水汽冷凝速率方程预测数据与现场实验数据比较。由于现场实验中空气湿度RH和空气-土壤温差ΔT处于变动中,为简化起见取平均值。考虑到遗址原土壤表面有白色盐结晶,使用含盐量为24.46 g/kg的水汽冷凝速率方程。
第一次实验平均湿度为90.1%、平均温差为14.399 ℃,各数据带入(3)式计算得到z值为0.133 kg·m-2·h-1。将第一次现场实验实际补水量换算成冷凝速率z为0.149 kg·m-2·h-1。实际补水量大于计算值约10%。
第二次实验分为四个阶段控制,各阶段平均温差分别为14.07 ℃、12.25 ℃、13.092 ℃、12.63 ℃,对应的平均空气湿度为81.652%、88.708%、93.972%、94.188%,分别带入(3)式计算得到四个阶段的z值为0.077 3 kg·m-2·h-1、0.092 6 kg·m-2·h-1、0.142 4 kg·m-2·h-1、0.137 1 kg·m-2·h-1。四个阶段的平均冷凝速率z为0.112 3 kg·m-2·h-1。将第二次现场实验实际补水量换算成冷凝速率z为0.118 kg·m-2·h-1。实际补水量大于计算值约5%。
实际补水量稍大于计算值的原因主要是:实际遗址土壤表面盐结晶的量比较多;另外实验过程中开盖测量数据时逃逸的水汽量未减去,尤其是第一次实验后期土壤表面温度升高期间逃逸的水汽量较多。
3 结 论
1) 本研究提出了一种新的土遗址保护理念,即通过适量补水维持土体内的水分平衡,使室内土遗址保持稳定。
2) 利用“气-液相变”原理,能够使气态水均匀地在土体内凝结成液态水,实现补水于无形。实验表明通过控制空气湿度、空气温度与土壤表面温度差,能够人工控制对室内土遗址的补水量,12~24 h内可以完全润湿土壤表层。对于含盐的土壤润湿速率更快。
3) 通过对21轮小实验结果进行归纳关联,得到以空气湿度RH(%)、空气-土壤温差ΔT(℃)和土壤含盐量S(g·kg-1)为变量,可以预测水汽冷凝速率z(kg·m-2·h-1)的四元方程。大致适用范围为:土壤含盐量0≤S≤25 g/kg、空气湿度60≤RH≤95%、空气-土壤温差7 ℃≤ΔT≤20 ℃。
4) 在萧山跨湖桥遗址博物馆遗址大厅内土遗址现场的局部实验表明,人工制作的冷凝补水控制设备可以实现“气-液相相变补水”的目标,使土壤表面的盐结晶在12 h内溶解并下渗。土遗址现场局部补水量与水汽冷凝速率方程预测值基本吻合。
5) 本研究仅仅是进行了一些试探性实验,如何实现更大面积土遗址的适量补水,还有许多研究需要深入。

