利用熵格式计算地下水溶质运移方程

陈荣三， 王凡芮， 邹 敏

(中国地质大学(武汉) 数学与物理学院， 湖北 武汉 430074)

对流-弥散方程是地下水溶质运移的控制方程.简单的理想的对流-弥散方程可以求出解析解，对于复杂的方程还要借助于数值方法.近年来，国内外学者针对对流-弥散方程提出了大量的数值方法，大致可以分成三类：Euler法、Lagrange法和混合Euler-Lagrange法.这些方法都能较好地解决弥散占优的问题.但是一旦对流占优，数值解会出现过量问题、过多的数值弥散和非物理振荡问题.

有限差分法、有限体积法和有限元法是三种比较常见的Euler方法.Roache[1]提出了上游加权法，该方法可以消除非物理振荡，但是增大了数值弥散.随后许多学者[2-3]提出了不同的上游加权法，上游加权对减小解的振荡作用有限, 但却会减低解的精度.为了提高解的精度,Brooks等[4]提出了沿流线上游加权的彼得罗夫-迦辽金方法.彼得罗夫-迦辽金方法在消除了数值振动现象的同时增大了数值弥散.梅一等[5]发展了一种带弥散因子的上游加权法，通过调整弥散因子可以控制非物理振荡但不降低解的精度.Leisman等[6]提出了引入人工扩散量和加权法，可以使得系数矩阵对称正定.刘扬[7]发展了带加罚函数的改进的Crank-Nicholson方法，该方法可以保证解的稳定性同时不会出现非物理振荡.成建梅等[8]总结了饱和水流中溶质运移方程求解的各种数值方法.焦甜等[9]分析了Crank-Nicholson方法，上游加权法和人工增量法的截断误差、稳定性和收敛性.Cheng等[10]将局部间断有限元方法推广到了对流-弥散方程的计算.

近几年来，茅德康等[11-16]针对双曲守恒性方程提出了一种Godunov型的熵格式.与传统Godunov不同的是，熵格式除了数值计算数值解外，还数值计算数值熵，通过数值模拟多个物理量可以从多个侧面来刻画物理过程.数值实验证明该方法可以有效地控制数值黏性并且适合长时间的数值计算，在保证数值稳定的同时最大程度上减少了数值弥散.崔艳芬等[10]对熵格式进行了数值分析，揭示了这种格式具有在计算中各步误差相互抵消的性质.

本文将熵格式推广到地下水溶质运移方程.首先采用分裂方法将地下水溶质运移方程分成对流方 程和弥散方程，对流方程是一个双曲型方程，利用熵格式求解，弥散方程的空间离散用二阶中心格式离散,时间离散用简单的向前差分离散.通过数值实验，对不同对流强度的地下水溶质运移方程进行了数值计算，计算结果表明,熵格式没有出现过量问题，没有出现非物理振荡，数值弥散小，特别适合强对流问题的数值计算.

1 熵格式的描述

考虑如下的地下水溶质运移方程[9]

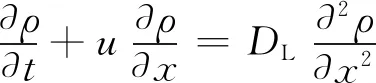
(1)

式中:ρ为质量浓度；DL为水动力弥散系数；u为速度；x为距离；t为时间.在式(1)两边同时乘以2ρ,整理得

(2)

这里U(ρ)=ρ2，把它称之为熵.熵格式是Godunov型有限体积格式，与传统的Godunov格式不同的是，熵格式有两个数值实体，即数值解和数值熵.也就是说，不仅要计算水溶质运移方程(1)还需要计算相应的熵方程(2).为了描述的简单，采用一致等分网格，网格的宽度为Δx，时间步长为Δt，第i网格单元为Ii=(xi-1/2,xi+1/2)，其中xi±1/2=xi±0.5Δx，xi表示网格中心.引入数值解ρi，n为网格单元Ii在tn时刻精确解的网格平均的近似，即

(3)

另外引入了一个数值熵Ui,n，它是对精确解的熵的网格平均的逼近，即

(4)

采用分裂的方法来求解式(1)和式(2)，将式(1)和式(2)分成对流部分和弥散部分.式(1)和式(2)的对流部分和弥散部分分别为

(5)

和

(6)

利用熵格式计算对流方程(5)，熵格式包含数值解ρi,n和数值熵Ui,n两个数值实体. 重构函数和ρi,n和Ui,n都有关.熵格式按照重构、发展和网格平均三步来进行.具体步骤如下：

(1) 重构.tn时刻第i个网格Ii内采用熵台阶重构，它是一个阶梯函数，如式(7)所示.

(7)

其中di,n为重构斜率. 显然，熵台阶重构式(7)自动满足

(8)

首先计算熵台阶di,n,e，要求

(9)

式(9)意味着重构解的熵的网格平均等于该网格的数值熵. 将式(7)代入式(9)可以计算出熵台阶di,n,e

(10)

di,n,e符号取为和(ρj+1,n-ρj-1,n)相同. 另外，定义一个总变差下降(TVD)的台阶di,n,TVD

di,n,TVD=min mod(ρi,n-ρi-1,n,ρi+1,n-ρi,n)

(11)

这里min mod定义为

min mod(a,b)=

(12)

最终的台阶取为di,n,e和di,n,TVD的最小值，符号取为和(ρi+1,n-ρi-1,n)相同，即

di,n=sgn(ρi+1-ρi-1)min(|di,n,e|,|di,n,TVD|)

(13)

(2) 发展.以重构函数R(x;ρn,Un)作为tn层的初值，求解以下初值问题:

(14)

定解问题(14)的精确解为v(x,t)=R(x-ut;ρn,Un).

(3) 网格平均. 在t=tn+1时的数值解和数值熵分别计算为

(15)

(16)

利用中心格式计算弥散方程(6)中的二阶导数，利用Euler向前差分进行时间离散.最终的格式为

(17)

(ρi+1,n-2ρi,n+ρi-1,n)

(18)

2 数值试验和结果分析

算例1 均匀流场[9].考虑如下地下水溶质运移问题，假设半无界均质砂砾，地下水的速度u是常数，初始质量浓度为0,左边界为质量浓度边界，右边界为0边界，即右无穷远处的质量浓度为0.该问题的解析解为

(19)

式中:ρ0=1 mg·L-1;u=6 m·d-1;DL=uα，α是纵向弥散率.

Peclet数定义为Pe=Δx/α，Pe是用来描述对流和弥散的相对大小，根据Pe的大小可以将对流-弥散方程分为两大类：当Pe>2时，称之为对流占优方程；当Pe≤2 时，称之为弥散占优方程.计算区域为[0,60] m，网格数取为30.图1～ 4是对流强度Pe分别为1、4、16、32，时间分别为1 d和4 d的数值解和解析解的质量浓度分布对比图，图中圆圈表示数值解，实线表示解析解.从图1～4中不难看出，熵格式没有出现过量问题，也没有出现非物理振荡，所产生的数值弥散比较小.随着对流强度的增加，数值解和解析解吻合得更好，这说明熵格式在处理强对流问题方面具有很大优势.

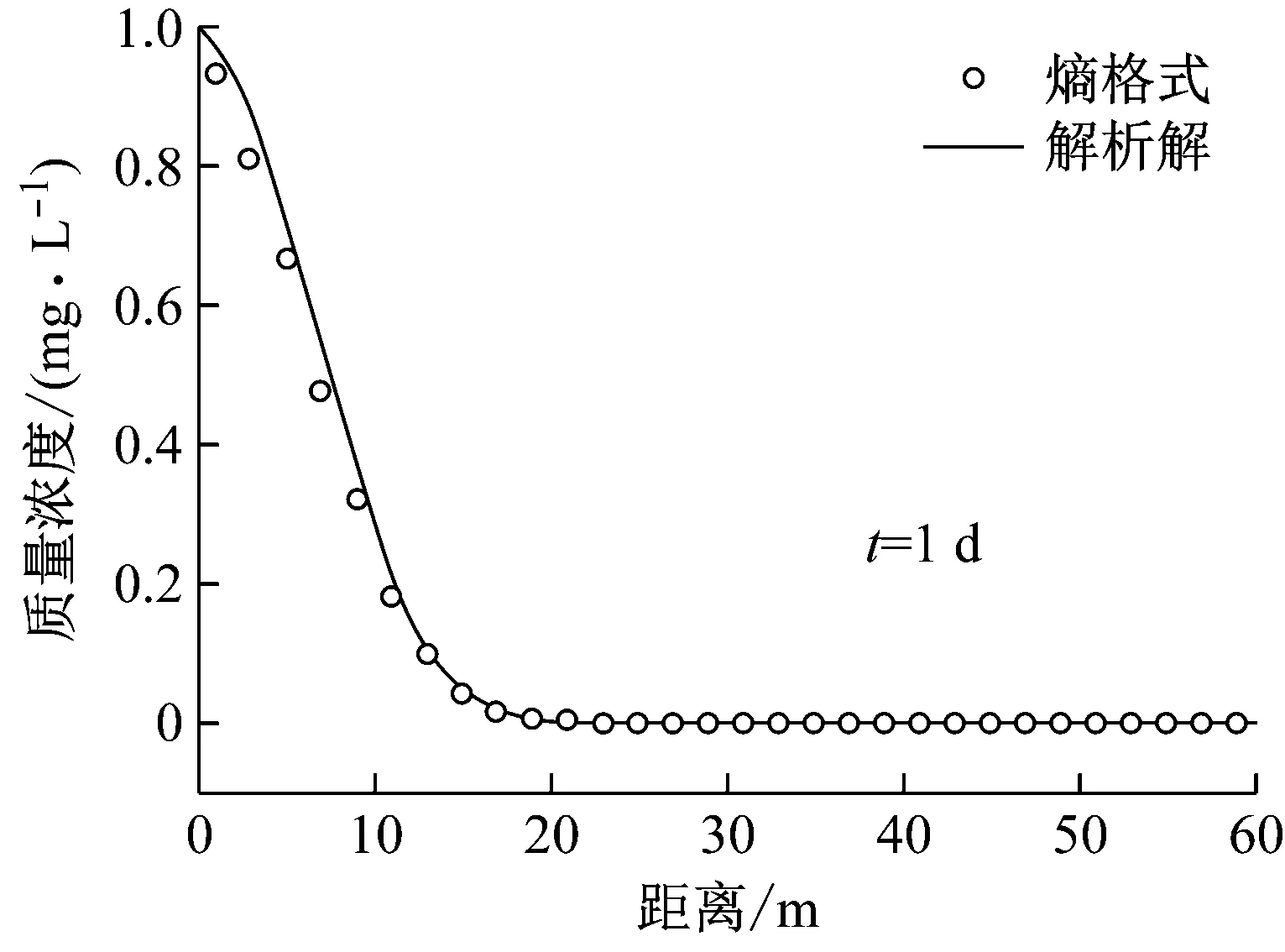
图1 Pe=1时质量浓度分布

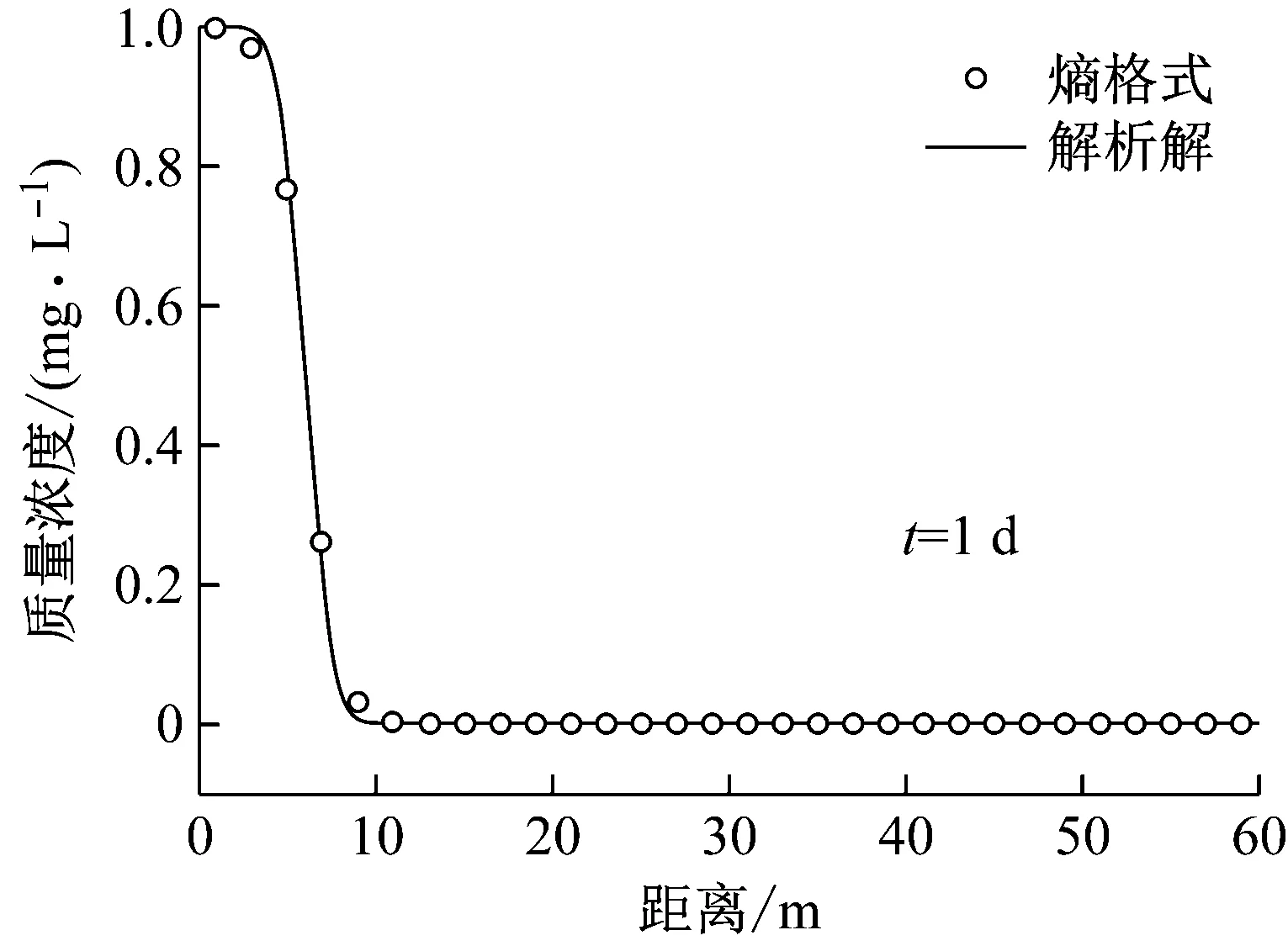
算例2 非均匀流场[7].考虑如下对流扩散问题

(20)

该问题的精确解为x(1-x)et.图5是t=0.6的数值解和解析解的对比图，图中圆圈表示数值解，实线表示解析解.从图5不难看出，数值解和精确解几乎重合，没有出现非物理振荡也没出现过量现象.

图5 t=0.6时质量浓度分布

3 结论

地下水运移方程可以用对流-弥散方程来刻画，当对流占优的时候，数值解容易出现过量和非物理振荡，一些能克服非物理振荡的格式往往会引入过多的数值弥散，使得解的精度降低.本文将针对双曲守恒型方程的熵格式推广到地下水运移方程的计算，具体做法是采用分裂的方法将地下水运移方程分成对流方程和弥散方程，对流方程利用熵格式求解，弥散方程用中心格式进行求解.数值试验表明,本文的格式不会产生过量问题也不会出现非物理振荡，特别适合强对流问题的数值计算.