几个代数等式对应的图形及应用

湖南省湖南师范大学数学与统计学院(410081)叶 军 闵福燕

我们知道,对于一个一元一次方程,在平面直角坐标系中会有一条直线与其对应,对于一个一元二次方程,在平面直角坐标系中会有一条抛物线与其对应.同样地,对于一些特殊的代数式,在平面中也会有相应的图形与其对应,有时将代数问题转化为平面几何问题来解决,会大大地降低解题难度,达到化繁为简的效果.下面我们来看几个引理和具体例子.

引理1对于三锐角A,B,C,cos2A+cos2B+cos2C+2 cos A cos B cos C =1 当且仅当A+B+C =π.

证明运用降次公式,原式等价于等价于运用积化和差公式,等价于cos2C +2 cos A cos B cos C +cos(A-B)cos(A+B)=0.对cos C 进行因式分解,等价于[cos C+cos(A+B)][cos C+cos(A-B)]=0.因为A,B,C为锐角,所以所以cos C+cos(A-B)＞0,故原式等价于cos C +cos(A+B)=0.等价于cos(A+B)=cos(π-C).又A+B,π-C ∈(0,π),且y =cos x 在(0,π)内单调递减,所以原式等价于A + B=π - C,等价于A+B+C =π,证毕.

下面给出几例关于如何将代数问题转化为几何问题并运用上面三角恒等式解题.

例1.1已知正实数p,q,r 满足关系式1,求证方程组有唯一解.

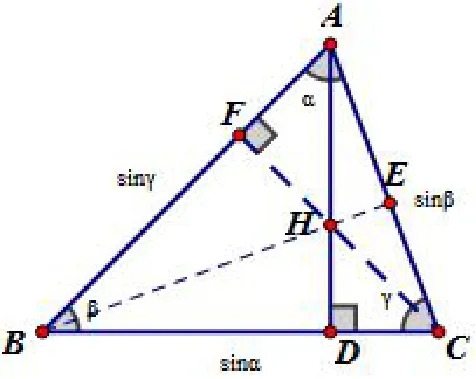
图1

解显然p,q,r ∈(0,1),令cos γ,其中则等式化为cos2α+cos2β+cos2γ+2 cos α cos β cos γ =1,由引理知,α+β +γ=π.由此可知,于是可构造一个三内角依次是α,β,γ,边长为sin α,sin β,sin γ 的△ABC(此三角形外接圆半径R 为).如图1所示.

例1.2设正实数x,y,z 满足x2+y2+z2+2xyz=1.令试求ab+bc+ca 的值.

提示首先,我们来证明一个锐角三角形内的恒等式cot α cot β + cot β cot γ + cot γ cot α=1.将上式通分,等 价 于 证 明tan α + tan β + tan γ=tan α tan β tan γ.而tan α+tan β+tan γ=tan(α+β)(1-tan α tan β)+tan γ =tan(π-γ)(1-tan α tan β)+tan γ =-tan γ(1-tan α tan β)+tan γ=tan α tan β tan γ,所 以 有cot α cot β + cot β cot γ +cot γ cot α=1.

解因为x,y,z 均为正实数,x,y,z ∈(0,1),且满足x2+y2+z2+2xyz=1.所以可令x=cos α,y=cos β,z =cos γ,其中则上面三式分别化简为=2 cot α,b=2 cot β,c=2 cot γ,则ab+bc+ca=4 cot α cot β +4 cot β cot γ +4 cot γ cot α=4.

例1.3设a,b,c ＞0,a2+b2+c2+abc=4.求证：恒为常数.

解先用赋值法计算出这个常数,不妨令a=b=c=1,则

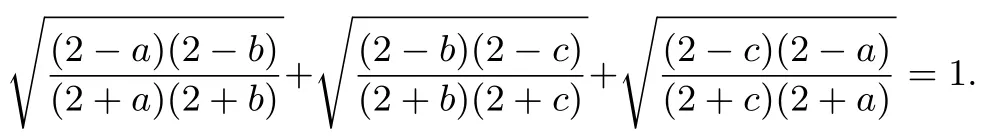
下面证明对于任意满足条件的a,b,c,

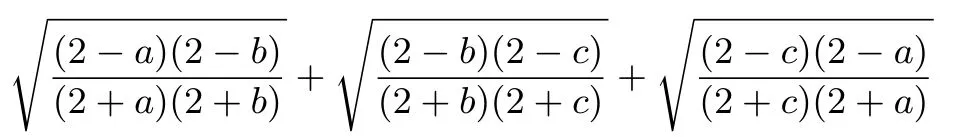
恒等于1.

因为a,b,c 均为正实数,a,b,c ∈(0,2),且满足a2+b2+c2+abc=4.所以可令a=2 cos α,b=2 cos β,c=2 cos γ,其中则上面三式分别化简为

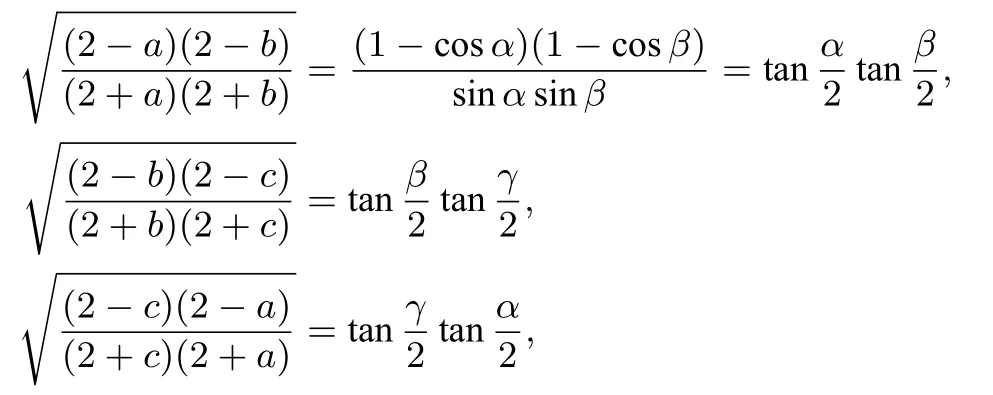
则

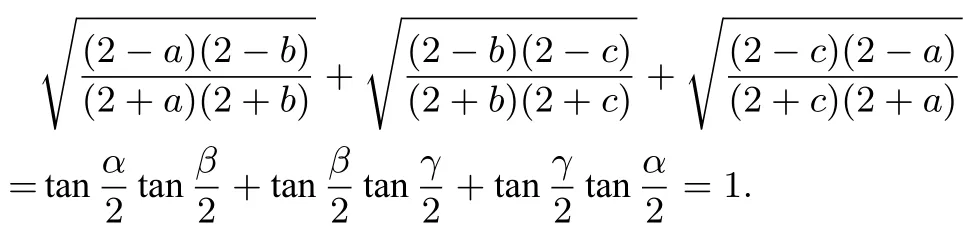
通过以上三例我们可以归纳总结出对于正实数x,y,z,若满足x2+y2+z2+2xyz=1 这种形式的代数式,则可以构造出一个锐角三角形ABC,使得x=cos A,y=cos B,z=cos C,这样就可以将代数问题转化成几何问题,会大大地降低解题难度,达到化繁为简的效果.

引理2若三个正实数a,b,c 满足a2=b2+c2-2bc cos α(0 ＜α ＜π),则以a,b,c 为边长可以构造一个△ABC.且α为b,c 两边的夹角.

此引理称为余弦定理的逆定理.

证明以a,b,c 为边长可以构成一个三角形的充要条件是由题目条件知a2=b2+c2-2bc cos α,又-1 ＜cos α ＜1,所以0 ＜b2+c2-2bc ＜a2＜b2+c2+2bc,即(b-c)2＜a2＜(b+c)2,所以|b-c| ＜a ＜b+c.由此可知,以a,b,c 为边长可以构成一个三角形,设此三角形为△ABC,其中角A,B,C 所对边长分别为a,b,c.则由余弦定理得而由题干知,所以cos A=cos α.又A,α ∈(0,π),故A=α.故以a,b,c 为边长可以构造一个△ABC.且α 为b,c 两边的夹角.

下面给出几例关于如何将代数问题转化为几何问题并运用余弦定理逆定理解题.

例2.1设正实数a,b,c 满足试求b2-ac 的值.

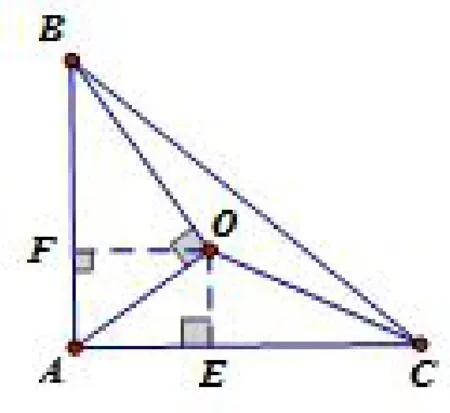
图2

解如图2,以O 为起点,作长度为a,b,c 的三条线段OA,OB,OC,使得∠AOB=90°,∠AOC=120°则∠BOC =150°.由余弦定理得,

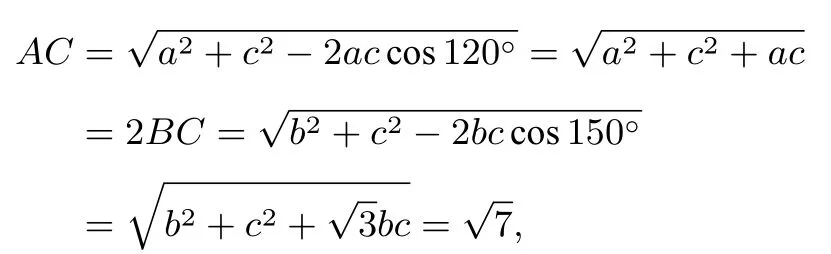
则易得∠CAB =90°,过O 作OE⊥AC,OF⊥AB.设AE =m,OE=n,易得∠ABO=∠OAE,所以即又有∠AOC=120°,所以tan ∠AOC =即

例2.2证明：对任意正实数x,y,z 有√

图3

证明联想到余弦定理逆定理以及三角形中两边之和大于第三边,我们可以构造图形,如图3,以O 为起点,作120°,则∠BOC=150°.由余弦定理有由于三角形中两边之和大于第三边,所以AB+AC ＞BC,即证得原不等式成立.

通过以上两例可以归纳总结出对于三个正实数a,b,c,若满足a2=b2+c2-2bc cos α(0 ＜α ＜π)这种形式,则可以构造出一个三角形△ABC,使得△ABC 三边长分别为a,b,c,从而将代数问题转化成几何问题,将抽象的代数式转化成图形直观的表现出来.

引理3在凸四边形ABCD 中,若AB·CD+BC·AD =AC ·BD,则A,B,C,D 四点共圆.此定理称为托勒密定理的逆定理.

图4

证明如图4所示,在凸四边形ABCD 中,取点E 使∠BAE =∠CAD,∠ABE =∠ACD,则△ABE ∽△ACD,即有即

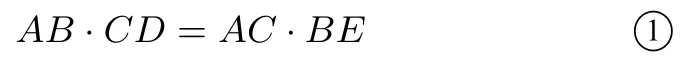
又∠DAE =∠CAB,有△ADE ∽△ACB,亦有

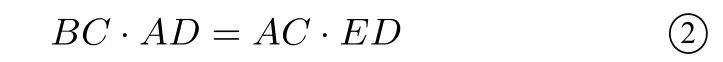
由 ①式和 ②式,注意到BE+ED ≥BD,有AB·CD+BC·AD =AC·(BE+ED)≥AC·BD.其中等号成立当且仅当E 在BD 上,即∠ABD=∠ACD.此时A,B,C,D四点共圆.证毕.

下面给出一例关于如何将代数问题转化为几何问题并运用托勒密定理的逆定理解题.

例3.1解方程

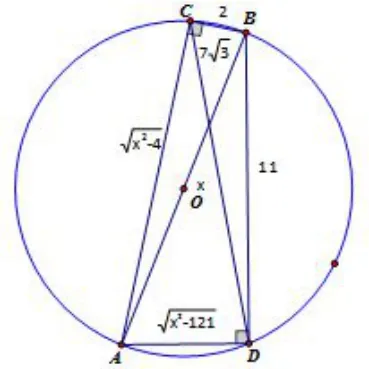
图2

解此等式具有ab+cd=ef 的形式,可以考虑运用托勒密定理的逆定理进行解答.由托勒密定理的逆定理知,以为边的四边形ACBD 四点共圆,且四边形两对角线长分别为如图5所示.又因为所以对角线AB 恰好是此外接圆的直径,且AB 的长度就是方程的解x.在△BCD 中,应用余弦定理得,所以∠BCD=120°,再应用正弦定理得

例3.2设a,b,c,d,x,y 为正实数,且满足xy =ac+bd,求证：

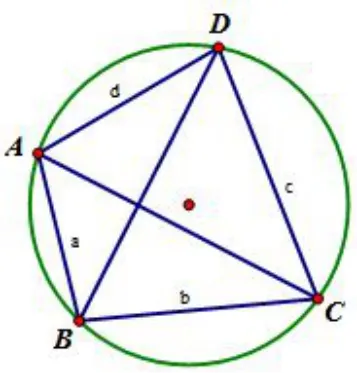
图6

分析对于代数式xy=ac+bd,运用托勒密定理的逆定理,可以构造一个圆内接四边形ABCD,其中a,b,c,d 为四边形ABCD 的四条边长,x,y 为其对角线的长.根据面积关系可以证明在此四边形ABCD 中,有

再通过考察欲证等式的几何意义,问题可以转化为证明rA+ rC=rB+ rD.其中rA,rB,rC,rD依次为△ABD,△BCA,△CDB,△DAC 的内切圆半径.这是本例的大致解题思路,具体的解题过程不再赘述,感兴趣的读者可以多多研究.

可见对于给定的具有ab+cd=ef 形式的代数式,可以考虑应用托勒密定理及其逆定理构造圆内接四边形,将代数问题转化成几何问题,将抽象的代数式转化成圆内接四边形表示出来,从而达到较好的解题效果.

从上面的引理和例题我们可以发现,对于一些特殊的代数式如三角恒等式、余弦定理及其逆定理、托勒密定理的逆定理等,在平面中都会有相应的图形与其对应,所以在今后的学习中遇到这类代数问题,可以尽量将其转化到平面几何上进行思考研究,可能会极大的降低解题难度.