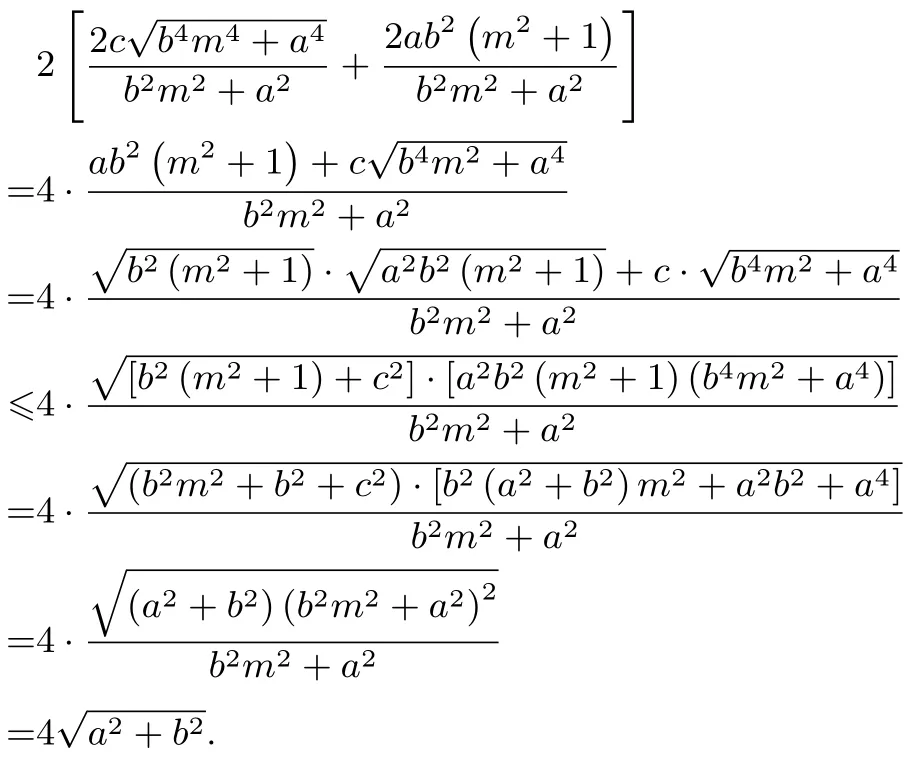过椭圆焦点的内接平行四边形的面积与周长问题的探究
广东省广东广雅中学(510160)杨志明
有关椭圆的内接平行四边形问题屡见不鲜,例如吕中伟等在文[1]通过如下三个引理:
引理1椭圆的平行弦的中点的轨迹是过椭圆中心的一条线段.
引理2设AB 是椭圆的弦.弦AB 所在直线的斜率k 存在且k /0,M 为弦AB 的中心,直线OM 的斜率为k′,则
引理3设A、B 为椭圆上的两点,OA⊥OB,则
得到了如下4 个定理:
定理1平行四边形内接于椭圆的充要条件是平行四边形的对称中心与椭圆的对称中心重合.
定理2椭圆不存在四边所在直线都有斜率的内接矩形.
定理3椭圆的内接菱形有一个公共的内切圆.
定理4椭圆内接平行四边形面积的最大值为2ab,这样的平行四边形有无数个,其中恰好一个为菱形、一个为矩形.
我校2019 届高三10月月考题的第20 题如下:
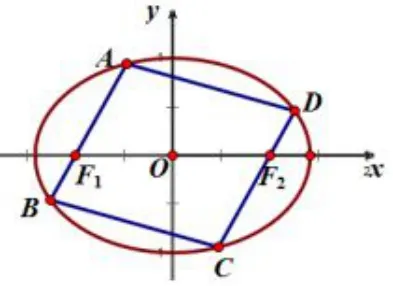
图1
(1)求椭圆E 的标准方程;
(2)过E 的左焦点F1作直线l1与E 交于A,B 两点,过右焦点F2作直线l2与E 交于C,D 两点,且l1//l2,以A,B,C,D 为顶点的四边形的面积S,求S 的最大值.
由此想到2018年广东省省际名校(茂名市)高考数学二模试卷(理科)的第20 题:
(1)求E 的方程;
(2)过E 的左焦点F1作直线l1与E 交于A,B 两点,过右焦点F2作直线l2与E 交于C,D 两点,且l1//l2,以A,B,C,D 为顶点的四边形的面积求l1与l2的方程.
可见,这两道题的第2 问均是有关过椭圆焦点的内接平行四边形的面积与周长问题,这引起了笔者的兴趣.有关椭圆的内接平行四边形的面积与周长问题已经解决,详见文[1-7].有约束条件的椭圆的内接平行四边形的面积与周长问题兹待解决.
问题1过椭圆的左焦点F1作直线l1与E 交于A,B 两点,过右焦点F2作直线l2与E 交于C,D 两点,且l1//l2,以A,B,C,D 为顶点的四边形的面积S,求S 的最大值.
解设l2: x=my + c,代入得(b2m2+a2)y2+ 2b2cmy - b4=0,Δ =(2b2cm)2+4b4(b2m2+a2)>0 恒成立.设C(x1,y1),D(x2,y2),则
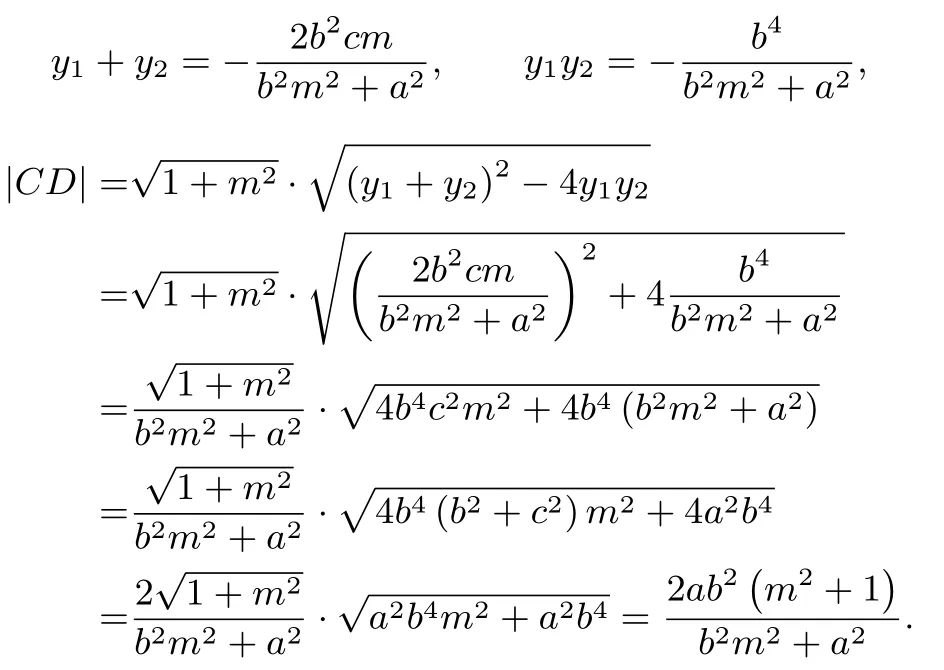
设l1的方程为x=my -c,则AB 与CD 之间的距离为由对称性可知,四边形为平行四边形,所以令则m2=t2-1,所以
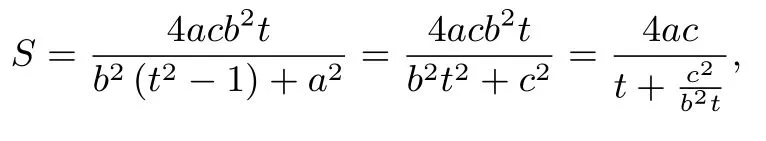
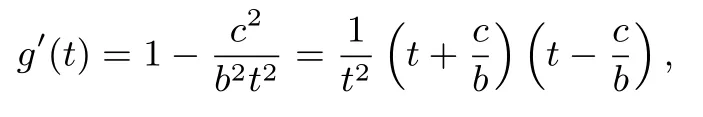
(i)若c ≤b 时,g′(t)≥0,g(t)是上的单调递增函数,

当且仅当t=1,m=0 时等号成立.
(ii)若c >b 时,令g′(t)=0,t =当1 ≤t ≤时,g′(t)<0,当时,g′(t)>0,
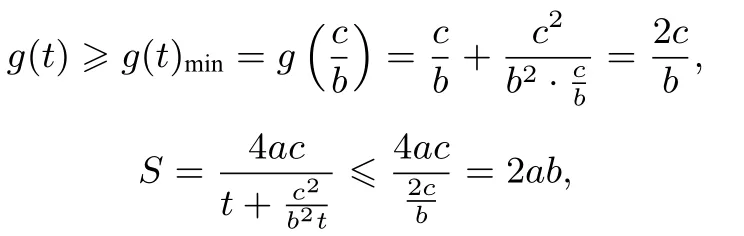
综上可知,当c ≤b 时,以A,B,C,D 为顶点的四边形的面积S 的最大值为当c >b 时,以A,B,C,D 为顶点的四边形的面积S 的最大值为2ab.
问题2过椭圆E :的左焦点F1作直线l1与E 交于A,B 两点,过右焦点F2作直线l2与E 交于C,D 两点,且l1//l2,以A,B,C,D 为顶点的四边形的面积S,求四边形ABCD 的周长的取值范围.
解当CD 垂直x 轴时,令x=c 得,此时,四边形ABCD 的周长是当CD 不垂直x 轴时,可设l2: x=my +c,代入得(b2m2+a2)y2+2b2cmy -b4=0,恒成立.设C(x1,y1),D(x2,y2),则A(-x1,-y1),则


故由柯西不等式知,四边形ABCD 的周长为