基于改进sinc插值的变PRF采样聚束SAR成像
陈世阳 黄丽佳 俞 雷
①(中国科学院电子学研究所 北京 100190)
②(中国科学院空间信息处理与应用系统技术重点实验室 北京 100190)
③(中国科学院大学电子电气与工程学院 北京 100049)
④(北京航空航天大学电子信息工程学院 北京 100191)
1 引言
合成孔径雷达(Synthetic Aperture Radar,SAR)作为一种重要的对地观测手段,具备全天时、全天候成像能力,被广泛用于高分辨率对地观测[1]。测绘带宽和分辨率是SAR系统两个重要的技术指标,如何同时实现宽测绘带与高分辨率是SAR系统技术的重要研究方向之一[2,3]。星载SAR的接收脉冲窗口必须避开发射脉冲窗口,否则将导致盲区的产生。然而即使采用方位多通道等技术,星载SAR测绘带依然受到固定盲区的影响[4-6]。在聚束SAR中,分辨率和斜视角的增加,将导致合成孔径时间和距离徙动单元(Range Cell Migration, RCM)的增大。系统设计中有的波位必须紧挨盲区,但由于RCM的影响某些方位位置的回波脉冲可能会超出接收窗;反过来为了保证所有的回波脉冲被完全接收,必须减小距离向测绘带宽。为了消除RCM对测绘带宽的影响,可以通过连续改变PRF使得盲区的变化更加分散。盲区位置和PRF选择具有确定性关系,固定PRF将导致固定的盲区分布,而PRF连续变化使盲区位置沿方位向变化,从而通过和距离多通道技术联合可以实现测绘带在地距方向连续拓宽[7,8]。此外将变PRF技术和高分辨率斜视星载SAR聚束模式联合可以保证测绘带宽同时减少回波数据量[9]。
变脉冲重复频率(Pulse Repetition Frequency,PRF)设计主要有周期性快变PRF、周期性慢变PRF和非周期性变PRF 3种设计方式。其中,周期性慢变PRF的设计准则是尽量减小PRF最大最小值差异,周期性快变PRF的设计准则是尽量避免接收脉冲连续丢失,非周期性变PRF设计准则是通过计算回波时序来避开收发干扰。处理变PRF采样回波信号的方式目前主要包括两种,一种是通过非均匀傅里叶变换(Non-Uniform Discrete Fourier Transform, NUDFT)逐点计算非均匀采样回波的频谱,然而NUDFT的缺点在于计算量巨大;另一种是恢复出均匀采样回波信号,继而采用频域算法进行批量化成像处理,包括线性插值方法、最优线性无偏估计(Best Linear Unbiased, BLU)方法、传统多通道重构方法、改进多通道重构方法、后向投影算法[10]等。线性插值方法重建会导致较大的信号失真,难以得到理想的重建结果;BLU方法通过对变PRF采样回波进行功率谱估计恢复出均匀采样回波,计算代价比较大,虚假目标抑制水平-40 dB[8]。多通道重构方法利用匹配滤波器组思想,首先将变PRF采样回波分解为多组均匀降采样的子信号,再通过子信号频谱的组合得到均匀采样信号的频谱。随着通道数和非均匀度的增加,多通道重构方法逐渐失效,而改进多通道重构方法通过减小处理频带个数,最小化方位模糊信号能量,保证均匀采样信号重构性能[11-13]。多通道和改进多通道方法基于子信号周期采样前提,难以解决非周期性变PRF采样回波重构问题[14]。
本文首先简单介绍了变PRF采样设计方式,建立了两组高分辨率星载SAR聚束模式回波的仿真参数;从NUDFT原理出发,推导了适用于带限信号的改进sinc插值核函数,并与sinc插值核函数进行了对比分析;利用聚束模式回波信号Dechirp后的带限信号特点,发展了基于改进sinc插值的变PRF采样聚束SAR两步算法,对算法复杂度进行分析,说明了本文算法在计算效率上的优势;最后,利用计算机仿真数据和抽取后的高分三号等效变PRF实际数据验证了算法的有效性和精确性。
2 变PRF设计
2.1 传统固定PRF设计方法和问题
传统SAR系统中脉冲重复频率常设为定值。PRF的选择会直接影响方位模糊度(AASR)与距离模糊度(RASR),PRF增大有利于降低AASR,而PRF减小有利于控制RASR,因此需要折中选择PRF,对PRF数值加以限制,避开发射干扰和星下点干扰[15]。其中,发射干扰对PRF的限制条件为

星下点干扰对PRF的限制条件如下
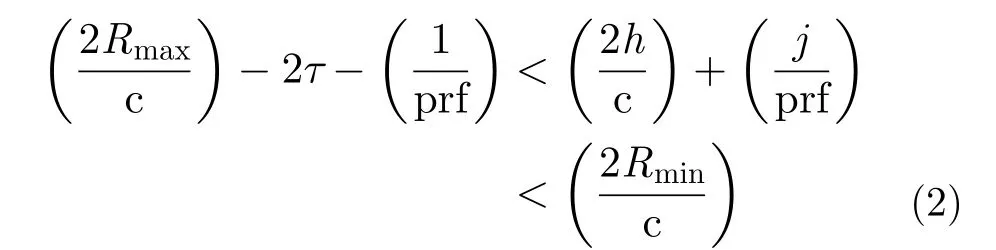
根据天线视角、测绘带宽、分辨率等需求,在满足一定模糊度指标的前提下,按照上述限制条件可以确定PRF。当PRF固定不变时,盲区位置不会随着瞬时斜视角的变化而变化,而测绘带对应的斜距范围却因雷达平台的移动而改变。因此,为了接收到所有的回波脉冲,系统所允许的最大测绘带宽对应时间宽度最大范围为

通过借鉴未来成像体系FIA-RADAR(Topaz)系列的星载SAR参数,其轨道高度约1100 km、雷达工作在X波段、发射脉冲时间宽度40 μs、分辨率标称值0.1 m、成像区域8 km×8 km。图1(a)给出PRF范围4500~6000 Hz、视角范围20°~50°时,排除星下点干扰和发射干扰后的PRF和时间关系的时序图。对于高波位,PRF选择相对困难。以49°视角正侧视为例,PRF取值5160 Hz时,可成像视角范围48.93°~49.07°、距离向幅宽约6 km,无法满足8 km×8 km成像区域的设计要求如图1(b)所示。随着斜视角的增大,距离可成像范围距离设计要求越远。而在斜视条件下,对可成像视角范围要求更大,使得PRF选择更加困难。
2.2 周期性变PRF设计方法和结果
周期性变PRF设计中,盲区通常沿着方位向均匀分布于整个测绘带内。变PRF采样(即生成变PRI采样序列)突破了传统发射干扰和星下点干扰形成的PRF设计约束,是一种实现高分辨率宽测绘带的有效手段。根据文献[8]给出的周期性慢变PRF设计方法和周期性快变PRF设计方法,建立星载SAR聚束模式的相关成像参数的推导过程将在后续讨论。
2.2.1 周期性慢变PRF
周期性慢变PRF的设计准则是:在尽可能减小PRF变化范围的前提下,使盲区在一个PRF变化周期内沿测绘带均匀分布。由于斜距越大,可选PRF数值范围越大,因此PRF最大值和最小值(和)满足如下条件
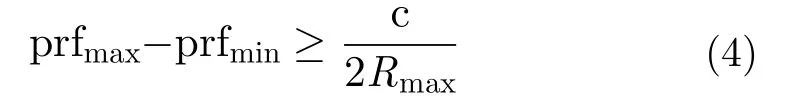
2.2.2 周期性快变PRF
周期性快变PRF设计的准则是:通过扩大PRF变化范围,实现盲区沿测绘带更加分散的同时保证脉冲不连续丢失。通过推导两个连续脉冲重复时刻的差值与回波的时序关系,周期性变PRF序列需要满足如下条件
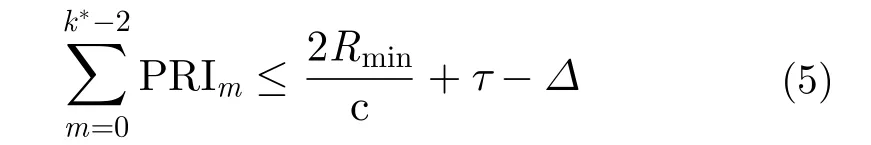

图1 固定PRF时,排除星下点干扰和发射干扰后的时序图Fig. 1 Illustration of PRF excluded zones as a result of transmit and nadir interference
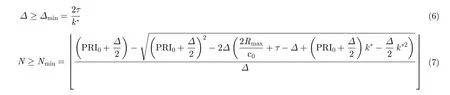
根据上述公式可以确认快变PRI序列的脉冲个数与相邻PRF变化间隔,即可完成快变序列的雷达参数设计。
2.2.3 变PRF参数设计
采用与2.1节中相同的轨道高度、雷达频段、发射时间宽度、分辨率、成像区域,根据2.2节的公式分析设计快变慢变对应的雷达参数,如表1所示。根据相应的参数,可以通过计算脉冲时序关系获得盲区分布如图2所示。

表1 快变慢变仿真参数Tab. 1 SAR parameters of two types of PRI variation
由图2(a)可以看出慢变PRF设计在尽可能缩小PRF变化区间的情况下使盲区均匀分布于测绘带内,但存在连续丢失脉冲的情况;而在图2(b)中可以看出快变设计使盲区更加分散,PRF变化范围远大于慢变的PRF变化范围,且实现不连续丢失脉冲的设计需求。
3 变PRF星载SAR聚束模式成像
3.1 基于改进sinc插值的非均匀采样信号重建
对于均匀采样信号,可以利用离散傅里叶变换(Discrete Fourier Transform, DFT)和快速傅里叶变换(Fast Fourier Transform, FFT)计算信号频谱[16]。当满足奈奎斯特采样条件时,sinc插值可准确重建连续信号在任一时刻的数值
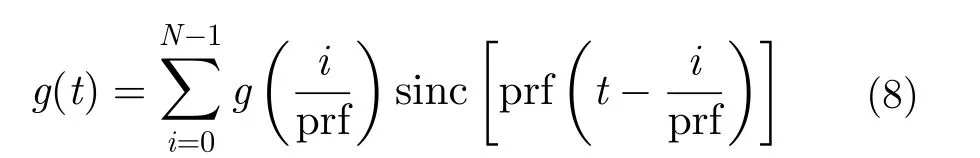
上述基于sinc插值的重建方法是以均匀采样为前提条件,无法适用于变PRF设计时信号频谱计算和分析。对于聚束模式SAR回波信号,多普勒域总带宽为合成孔径内多普勒带宽与场景多普勒带宽之和,PRF设计值大于场景多普勒带宽但远小于总多普勒带宽,信号在多普勒域产生频谱混叠。采用Dechirp操作去除了合成孔径内的多普勒带宽,剩余为场景多普勒带宽,此时回波信号满足带限条件,方位向回波信号表达式为
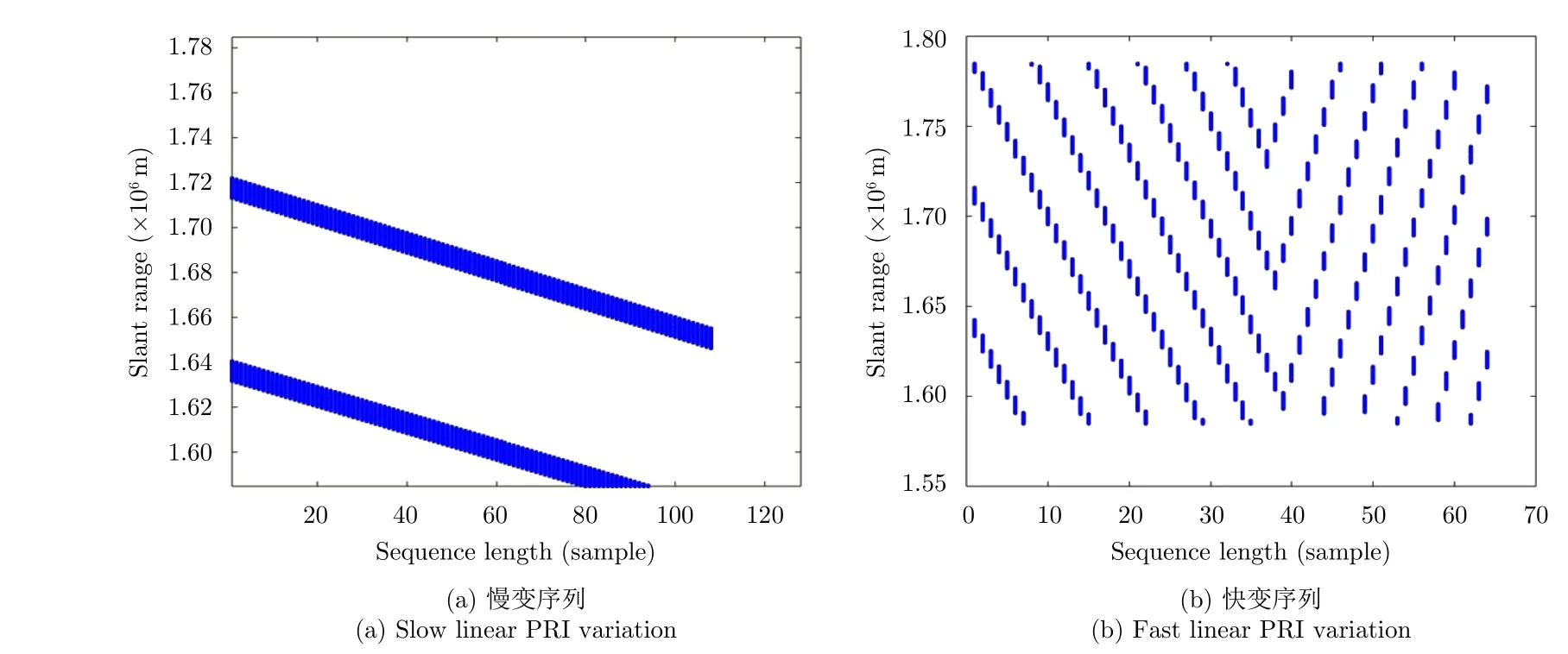
图2 给定参数下的盲区分布图Fig. 2 Blind ranges location for a given parameters of different PRI variations

对于非均匀采样的方位向回波信号,采用非均匀采样离散傅里叶变换(Non-Uniform Discrete Fourier Transform, NUDFT)近似获得信号频谱:
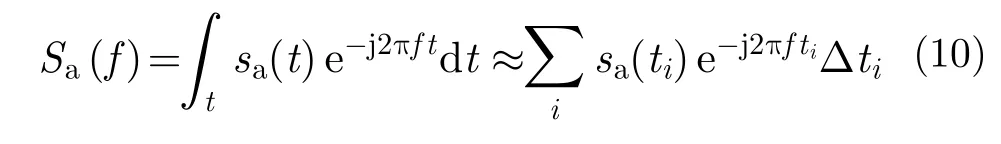
将式(9)代入式(10)中,经过整理可得

通过对比式(10)与式(11),可得非均匀采样信号的重构表达式
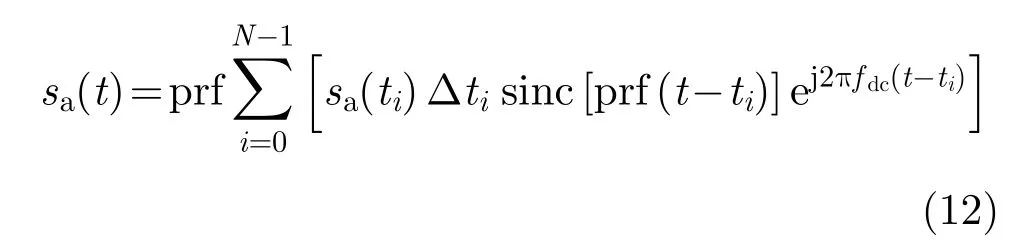
由于改进sinc插值核函数的幅度随采样距离增大呈sinc形式迅速衰减,因此可以利用有限采样点对任一时刻的信号复数值进行近似恢复。理论上,改进sinc插值核长度越长,信号重建越精确,插值核长度越短,计算效率越高。实际应用中,需要综合考虑精度和效率的要求,对插值核长度进行折中选择。基于表1给出的仿真参数,插值核长度设置为32时即可获得较好的插值效果、得到较好的成像结果,继续增加核长度则对插值精度提高作用非常有限。
改进sinc插值的计算量与NUDFT的计算量统计见表2。其中,表示方位向采样点数,表示插值核长度。两种算法的运算量比值为由于核插值长度远远小于采样点数,即可见改进sinc插值相对于NUDFT计算量大幅降低。

表2 计算量对比Tab. 2 Complexity of calculation
3.2 基于改进sinc插值的两步成像算法
通过波束导引技术,使波束长时间照射目标区域,实现聚束模式,可以突破条带模式成像分辨率限制,获得目标区域高分辨率成像结果。由于波束中心的转动,导致多普勒中心频率改变,整个场景多普勒带宽增大,按照场景瞬时带宽设计PRF导致方位频谱混叠。两步式成像算法的关键在于Deramp操作:通过参考信号对原始回波信号完成方位向卷积操作,去掉波束中心引入的多普勒带宽,使得方位向信号频谱解混叠变为带限信号。
假设SAR发射的线性调频信号基带形式为


为了消除方位向残余多普勒带宽,采用Deramp操作对雷达回波进行处理,采用回波信号的共轭形式对信号进行卷积操作,实际应用中由于卷积操作运算量巨大,通常采用时域参考函数相乘再通过傅里叶变换进行频域滤波,如下所示

然后,对信号进行频域补零操作完成信号升采样并对PRF进行重新计算。紧接着,在距离多普勒域进行残余相位校正后,信号恢复为多普勒域无模糊的回波信号,可以沿用条带模式的cs算法成像流程完成成像。
然而针对非均匀采样信号,式(15)无法获取准确去斜后的信号频谱,但信号已变为带限信号。
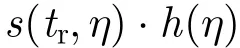
4 仿真结果
4.1 仿真验证
首先,利用点目标回波仿真验证基于改进sinc插值的两步式成像算法的有效性。仿真参数分别采用表1中的快变与慢变雷达参数。方位向成像场景共8 km,在仿真中沿方位向设置了3个点目标,间距4 km,分布于整个成像场景之中。
4.1.1 慢变非均匀采样结果
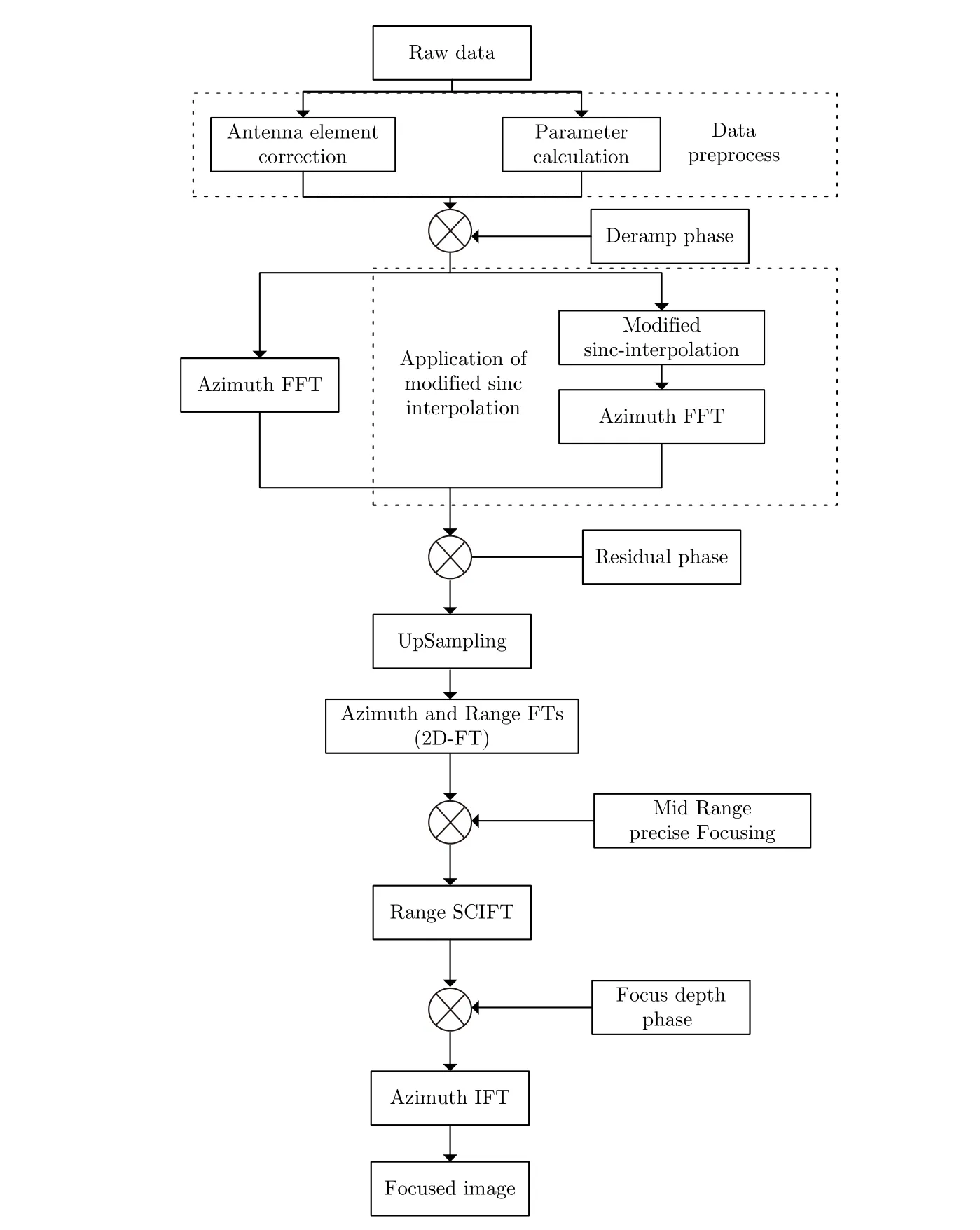
图3 基于改进sinc插值的两步式成像算法流程图Fig. 3 Procedure of the two-step processing approach based on the modified sinc interpolation
图4为利用慢变PRF设计所计算的参数,仿真得到的慢变PRF点目标成像结果。采用传统两步式成像算法进行成像后,方位像包络如图4(a)所示,在主像附近出现了很多虚假目标。采用传统sinc插值将非均匀信号恢复成均匀信号,再利用传统两步式成像算法进行成像处理后,方位像包络如图4(c)所示。虽然虚假目标电平略有下降但是成像质量仍下降明显。对慢变采样信号直接进行NUDFT计算频谱完成脉冲压缩结果如图4(b)所示,旁瓣电平下降明显。通过在两步式成像算法中结合改进sinc插值,虚假目标电平也下降到与NUDFT相当的水平如图4(d)所示。
4.1.2 快变非均匀采样结果
图5为利用快变PRF设计所计算的参数,仿真得到的快变PRF点目标成像结果。采用传统两步式成像算法进行成像后,方位像包络如图5(a)所示,旁瓣电平非常高。对快变采样信号直接进行NUDFT计算频谱完成脉冲压缩结果如图5(b)所示,成像结果较为理想。采用传统sinc插值将非均匀信号恢复成均匀信号,再利用传统两步式成像算法进行成像处理后,方位像包络如图5(c)所示,虚假目标电平仍然维持在较高水平。通过在两步式成像算法中结合改进sinc插值,虚假目标电平下降明显,如图5(d)所示,与NUDFT成像性能相当。
根据实验参数计算NUDFT与改进sinc插值的计算量,不论快变还是慢变模式下,可以看出改进sinc插值相比NUDFT约减少了1735倍的计算量。所有算法经测试得到的假目标电平如表3所示,可见无论是快变PRF还是慢变PRF的变PRF设计方式,通过结合改进sinc插值方法,虚假目标均被有效抑制,相比传统两步式成像算法与传统sinc插值,假目标电平下降明显,达到了与NUDFT相当的虚假目标抑制水平。
4.2 实际数据的处理结果
通过对高分三号的实际数据进行抽取,构造为非均匀采样数据,然后分别通过传统两步式成像算法和结合改进sinc插值的两步式成像算法完成成像,成像结果如图6所示。原始均匀采样数据通过传统两步式算法可以实现亚米级分辨率成像,如图6(a)所示;为形成变采样数据,周期性对实际数据进行置零,然后对置零后的数据直接采用两步式成像算法得到成像结果如图6(b)所示;采用基于改进sinc插值的两步式成像算法得到成像结果如图6(c)所示。
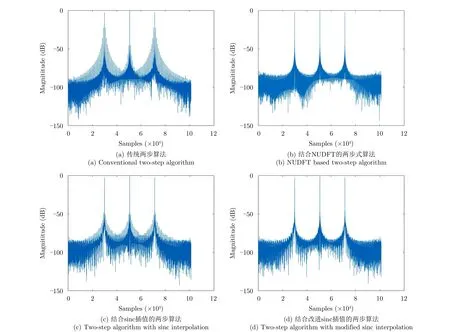
图4 慢变PRI序列两步式成像方位包络Fig. 4 Azimuth envelope of slow PRI change by different two-step algorithms
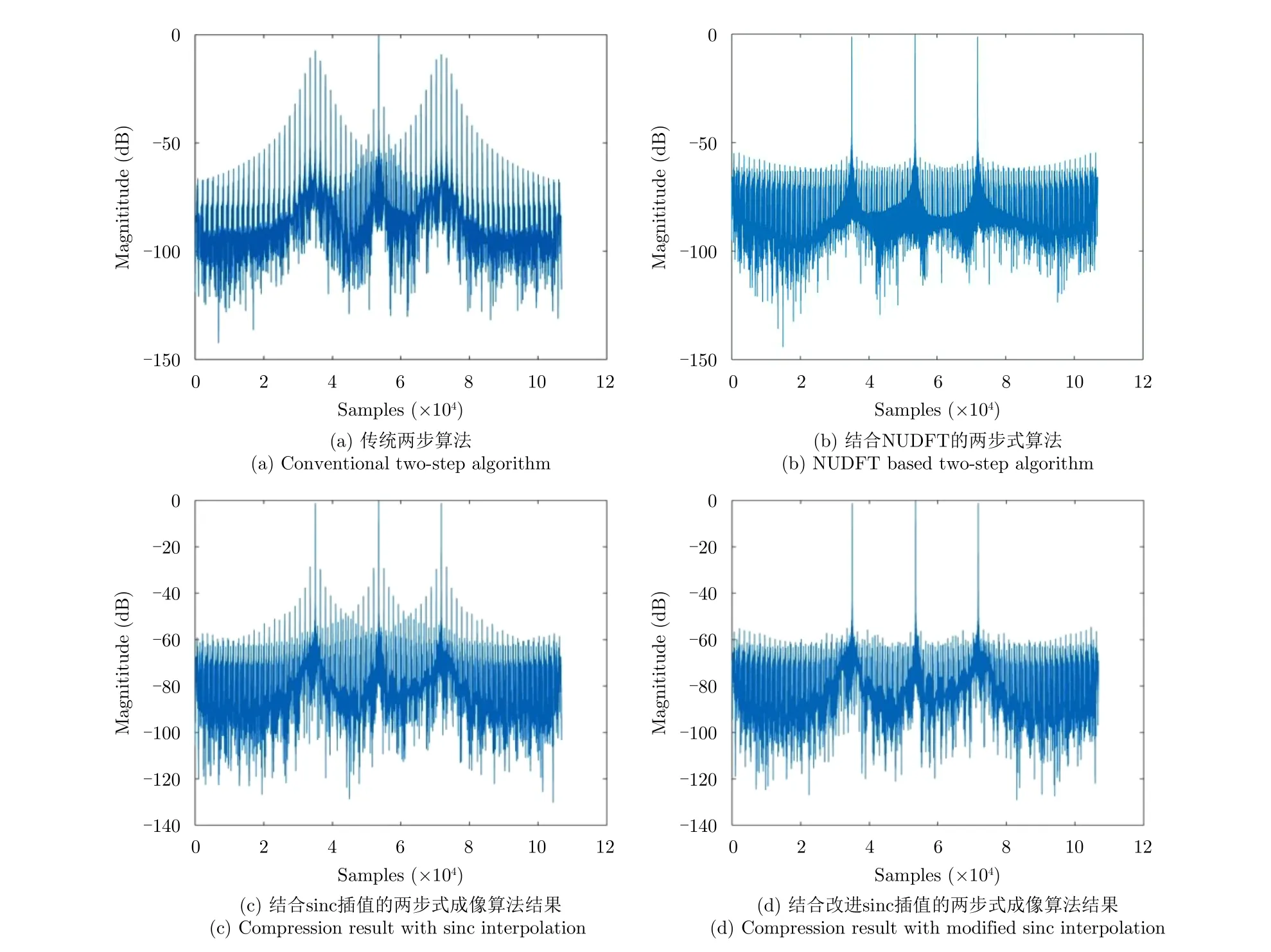
图5 快变PRI序列两步式成像方位包络Fig. 5 Azimuth envelope of fast PRI change by different two-step algorithms

表3 虚假电平指标测量结果Tab. 3 Estimation of false targets level

图6 高分三号数据处理结果Fig. 6 Experiments on GF-3 data
由上述仿真结果可知,采用传统两步式成像算法对于非均匀采样实际数据进行成像,会出现如图6(b)的方位向模糊等成像质量恶化问题,通过本文提出的改进sinc插值结合两步式成像算法进行成像结果如图6(c),可以看出与原始图6(a)差异不大,进一步证明了算法的有效性和精确性。
5 结论
本文主要讨论了星载SAR聚束模式下变PRF非均匀采样回波信号的成像处理问题,提出了一种基于改进sinc插值核的非均匀信号重构方法,该方法能够直接在时域将非均匀采样信号恢复为均匀采样信号。由于改进sinc插值核具有快速衰减性,通过选择合适的插值核长度,该方法运算量相比于NUDFT运算量降低了2~3个数量级。结合聚束模式两步式成像算法,利用改进sinc插值对Dechirp后的多普勒域带限信号进行重构,建立了基于改进sinc插值的两步式成像算法,拓展两步式算法对于非均匀采样信号的适用性。理论分析和试验分析表明,基于改进sinc插值的两步式成像算法可以得到良好的成像结果。本文提出的基于改进sinc插值的非均匀信号重构方法也可以应用于方位多通道等体制中,通过与现有成像算法的有机结合形成适用于变PRF设计的新的成像算法。

