组网雷达多帧检测前跟踪算法研究

王经鹤 易 伟 孔令讲

(电子科技大学信息与通信工程学院 成都 611731)

1 引言

多传感器融合通过利用多个节点的信息，实现传感器间信息互补。相比于单传感器，多传感器系统能够增加量测的维度和置信度，提高系统容错性和鲁棒性[1，2]。近几十年，多传感器融合受到了广泛的关注，也被应用到越来越多的领域当中[3-10]。其中，组网雷达系统(Netted Radar System， NRS)就是一种典型的例子[11]。组网雷达通过网内多个雷达协同探测，获取目标多向散射系数，能够大幅提高对目标的检测跟踪能力。目前，组网雷达系统多采用先检测后跟踪(Detect Before Track， DBT)的方法，即，本地雷达节点在每个时刻对接收到的回波信号进行单周期门限检测，得到一些可能是目标的虚警点迹，然后传递这些点迹或者由这些点迹跟踪滤波得到的目标航迹到融合中心进行融合[4，5]。本文定义这种方法为基于先检测后跟踪的多传感器融合(Multi-Sensor Fusion based on DBT， MSFDBT)。MSF-DBT在高信噪比下具有良好的性能，但当信噪比较低时，目标往往很难通过单周期门限检测，造成本地节点信息损失，导致算法性能严重下降。

解决DBT导致的性能损失的一个有效方法是采用多帧检测前跟踪技术(Multi-Frame Track Before Detect， MF-TBD)[12-14]。MF-TBD在每个时刻不对回波数据进行门限检测，而是联合处理多周期原始回波数据，然后输出目标检测结果[12]。由于MF-TBD不对单周期回波数据进行检测，因此可以更大程度地保留和利用目标信息；另一方面，它能够联合利用目标在多帧之间的运动相关性积累目标能量同时抑制噪声改善信噪比。因此，MF-TBD对低信噪比目标具有很好的检测能力。

但目前，MF-TBD主要应用在单传感器系统中，文献[15-17]研究了利用原始数据或中间结果在融合中心进行MF-TBD的方法，但并未考虑传递本地MF-TBD的检测结果到融合中心进行融合的情况。不同于MSF-DBT， MF-TBD输出的结果既不是虚警点迹也不是跟踪滤波后分布已知的目标航迹估计，而是一系列离散的点迹序列且分布未知[18]。因此，现有的融合算法并不直接适用于点迹序列的融合。

针对上述问题，本文对组网雷达下的目标检测跟踪算法进行研究，提出了一种基于点迹序列融合的组网雷达多帧检测前跟踪算法(Netted Radar System Multi-Frame Track Before Detect based on Plot Sequence Fusion， PSF-MF-TBD)，并给出了PSF-MF-TBD的粒子滤波实现方法。本文是对文献[19]的扩展，在文献[19]的基础上，改进了信号模型，并且对算法进行了更详细的理论推导，同时结合组网雷达系统模型及其问题对算法进行了补充和完善，最后通过仿真实验对算法进行了验证。

2 目标与信号模型

2.1 目标运动模型

2.2 回波信号模型

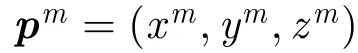
3 基于点迹序列融合的组网雷达多帧检测前跟踪算法

本节介绍PSF-MF-TBD算法。如图1所示，PSF-MF-TBD算法由两部分构成：本地多帧检测前跟踪和融合中心的点迹序列融合。

3.1 本地检测前跟踪

图1 PSF-MF-TBD算法结构框图Fig. 1 Block diagram of PSF-MF-TBD

3.2 融合中心的点迹序列处理

各雷达节点在完成本地MF-TBD后，将得到的点迹序列传递至融合中心做进一步融合处理，得到目标全局状态估计。由于MF-TBD输出结果既不是单帧检测后的离散点迹，也不是跟踪滤波后分布已知的准确目标航迹估计，因此现有的融合方法并不适用。另外，受雷达拓扑结构、系统参数等的影响，不同节点间的点迹序列还面临着时间异步、空间错位等多种问题，无法直接进行融合。针对这些问题，本节给出融合中心的点检序列处理方法，具体流程如图2所示。

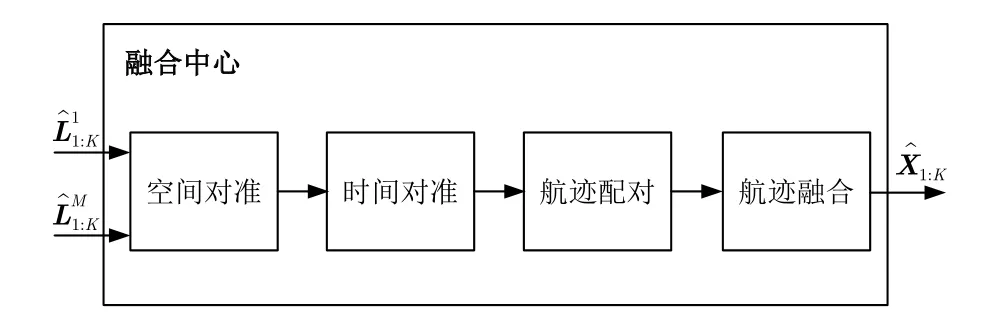
图2 PSF-MF-TBD算法流程示意图Fig. 2 Steps of PSF-MF-TBD

3.2.1 空间-时间对准

3.2.2 航迹配对

经过前面的空间对准和时间对准后，可以得到同一坐标系下，不同雷达在同一时间节点的检测结果。此时可以进行航迹配对。航迹配对主要是对不同雷达的输出结果按照一定准则两两配对，找到同一个目标在不同雷达下的检测结果，为后续的航迹融合做准备。配对准则的确定和配对顺序的设计是该步骤的两个关键点。

(1)配对的准则：本文选择两条航迹的位置误差作为配对标准。如果各时间节点的位置误差都在允许的范围内，则认为两条航迹属于同一目标。如果一条航迹无法和其它航迹配对，认为其是虚警，将它删除。

(2)配对的顺序：由于值函数大的状态更有可能是目标状态，因此在配对时，先选择值函数最大的航迹与其它航迹配对，配对成功后删除这两条航迹，然后重复上面的操作。

3.2.3 航迹融合

经过航迹配对后，每个目标都可以找到不同雷达对它的检测结果(点迹序列)。利用这些结果进行融合，能够得到目标状态全局估计。本文采用最小均方误差估计(Minimum Mean Square Error，MMSE)准则来实现这一目的。目标的全局估计表示为

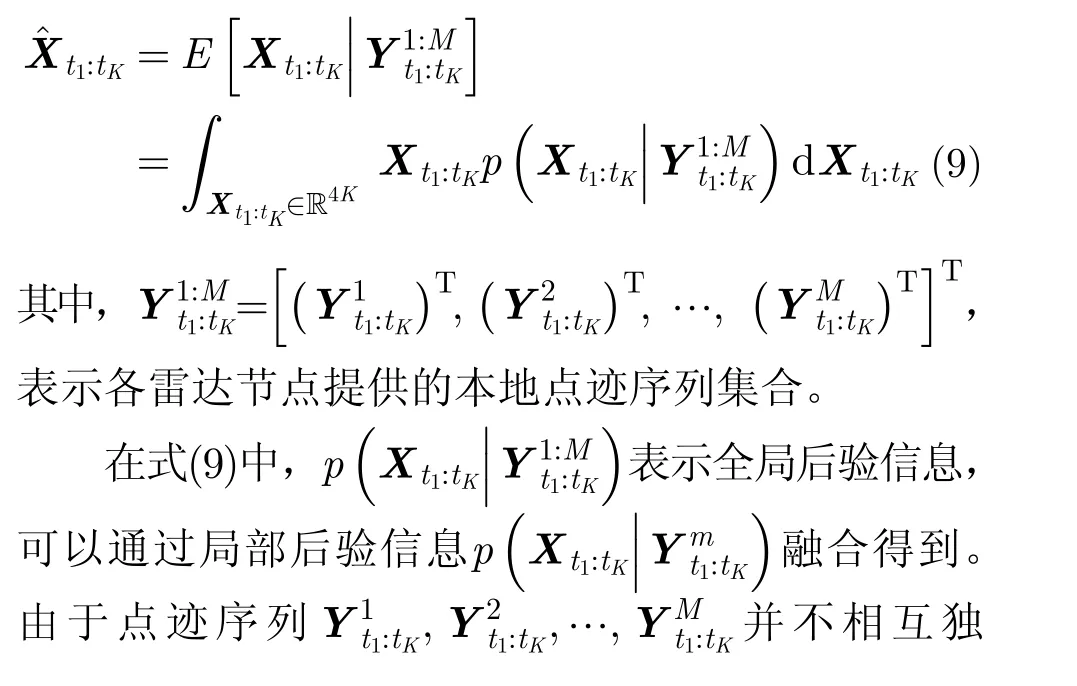
4 基于粒子滤波的点迹序列融合算法实现

上一节介绍了PSF-MF-TBD的基本理论，本节研究算法的实现方法。由3.2.3节可以看出，要实现点迹序列的融合，就要求解式(9)。本节首先研究式(9)中的MMSE求解问题，然后给出算法的粒子滤波实现方法。

4.1 MMSE问题求解

首先，本文给出下列结论。

其中，C是一个常数，由式(12)给出

将式(13)代入式(10)，再经过一些数学变换，即可证明式(11)。 证毕

4.2 粒子滤波实现算法

将式(11)和式(19)代入到式(18)，可以得到

式(20)的证明与单传感器场景中类似[20]，这里不再赘述。

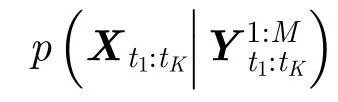
表1 基于粒子滤波的点迹序列融合算法Tab. 1 Plot sequence fusion based on particle filter

5 算法实现复杂度分析

6 仿真实验分析

本节对提出的PSF-MF-TBD进行性能评估分析，并将其与传统的先在本地进行单帧检测和卡尔曼滤波然后在融合中心进行航迹融合的MSFDBT算法进行对比。此外，为了验证本文提出的基于粒子滤波的点迹序列融合算法的有效性，仿真中还考虑了另外一种融合方式作为对比，即对多个雷达节点的点迹序列取平均值(称为平均融合)

仿真中采用文献[18]中的方法对本地点迹序列进行建模，即

在仿真中假设目标高度为0，即目标在2维X-Y平面运动。仿真场景如图3所示。仿真参数为：雷达1位置为(0.12， 0.24) km，雷达2位置为(6.00， 4.80) km，雷达1和雷达2的工作频率为1 GHz，脉冲重复频率为5000 Hz，带宽为2 MHz(距离分辨率75 m)，方位分辨率0.5°，扫描周期为1 s，起始扫描时刻相同。目标的初始位置为(1.80， 6.00) km，初始速度为(120， 60) m/s，目标做近似直线运动，过程噪声服从高斯分布，均值为0，协方差矩阵为

图3 仿真场景示意图Fig. 3 Sketch map of the simulation scenario

图4中给出了一次仿真中算法在各步处理后的仿真结果示意图，仿真中目标信噪比8 dB， MF-TBD联合处理帧数K=15，粒子数Q=800。图4(a)，图4(c)和图4(b)，图4(d)分别给出了雷达1和雷达2在一个多普勒频率上的单帧回波数据示意图，和在本地利用MF-TBD积累后的值函数示意图。可以看出，由于目标信噪比比较低，单帧回波数据中目标被淹没在噪声中，难以发现。但经过多帧积累后，由于目标能量被渐渐积累而噪声被抑制，因此目标逐渐凸显处理，积累后的值函数形成一个山峰状，而峰值点即为目标位置。对比图4(a)，图4(c)和图4(b)，图4(d)，能够证明本地利用MF-TBD算法的确可以改善目标信噪比，使弱小目标更容易被发现，进而提高检测概率。图4(e)和图4(f)中分别给出了雷达1和雷达2，对值函数检测后输出的本地点迹序列估计。从图中可以看出，首先，MF-TBD处理可以给出基本准确的目标航迹估计。此外，与文中所述相符，由于不同雷达节点相对目标的位置不同，而每个雷达观测到的目标位置又都是建立在以自己为中心的极坐标系下，因此，不同雷达节点的本地点迹序列估计是不一样的，无法进行直接融合。图4(g)中给出了不同雷达节点的点迹序列做了空时对准后的结果示意图。可以看出，空时对准后各雷达节点的点迹序列估计被统一到了相同坐标系下，并且基本可以与真实目标航迹吻合(但存在一定偏差)。此时已经可以对航迹进行配对和融合。图4(h)中给出了融合后的全局估计结果，融合后算法提供了更加精确的目标航迹估计。

图4 仿真中算法各阶段处理结果展示Fig. 4 Results of a single Monte Carlo run

图5比较了MF-TBD和SFD在本地雷达节点的检测概率。可以看出，因为联合处理帧数越多，能够利用的目标信息就越多，因此MF-TBD性能随联合处理帧数增长。总地来说，相比于SFD， MF-TBD有4～6 dB左右的性能增益。

图6对比了PSF-MF-TBD和MSF-DBT算法的RMSE，其中PSF-MF-TBD联合处理帧数K=15，节点数M=2，粒子数Q=800。可以看出，当信噪比较低时，两种方法的RMSE均随着时间增长；当信噪比较高时，它们的RMSE能够比较快地达到稳定。但不管在哪种情况下，PSF-MF-TBD的RMSE始终要小于MSF-DBT算法。这是因为MFTBD在本地的检测概率更高，其可以获得更多的目标信息。

图7给出了PSF-MF-TBD的在不同雷达节点数目下的RMSE，其中目标SNR=10 dB，算法联合处理K=15帧数据，粒子数目Q=800。可以看出，算法的RMSE会随着雷达节点的增多而减小。这是因为雷达节点越多，可利用的目标信息也越多，因此估计会越准确。图8中给出了算法RMSE随粒子数目的变化关系，其中目标SNR=10 dB， MF-TBD联合处理K=15帧数据，雷达节点数目M=2。因为粒子数目越多，对后验分布近似得越准确，因此算法的估计性能也越好。但从图8(b)中可以看出，当粒子数目足够多时，算法性能趋于饱和，在不同粒子数下的性能差异非常小。

图5 不同信噪比下MF-TBD与SFD检测性能对比Fig. 5 Detection probability of MF-TBD and SFD for different SNR

图6 PSF-MF-TBD与MSF-DBT的RMSE对比Fig. 6 RMSE of PSF-MF-TBD and MSF-DBT

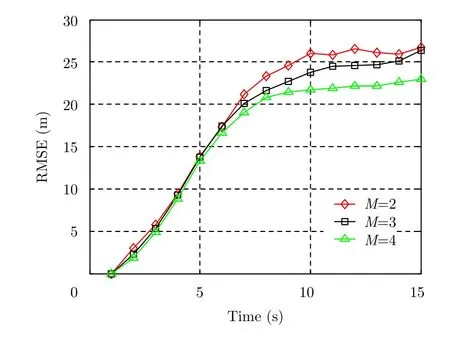
图7 PSF-MF-TBD在不同雷达节点数目下RMSEFig. 7 RMSE of PSF-MF-TBD under different number of radar nodes

图9中对比了单站雷达MF-TBD，平均融合方法，以及本文提出的PSF-MF-TBD算法的RMSE。仿真中，MF-TBD联合处理帧数K=15，粒子数目Q=800。可以看出，对比单站雷达MF-TBD，两种航迹融合方法的RMSE都有所降低。3种方法中，本文提出的PSF-MF-TBD算法的RMSE最小，相比于单传感器MF-TBD算法，其跟踪精度提高了50%左右，证明了其算法的有效性。

7 结论

本文针对组网雷达弱小目标检测跟踪问题，提出了PSF-MF-TBD算法。该方法首先在本地雷达节点进行多帧检测前跟踪处理，提高弱小目标的发现概率，然后传递检测结果，即点迹序列，至融合中心进行融合，提高目标的航迹估计精度。文中首先给出了算法的理论推导，然后结合实际雷达系统，给出了算法的具体处理流程。最后，为了有效解决点迹序列的融合问题，提出了算法的粒子滤波实现方法。仿真证明，相比于现有组网雷达算法，该方法能够同时改善目标的检测概率和跟踪性能。

图8 PSF-MF-TBD在不同粒子数下的RMSEFig. 8 RMSE of PSF-MF-TBD under different number of particle

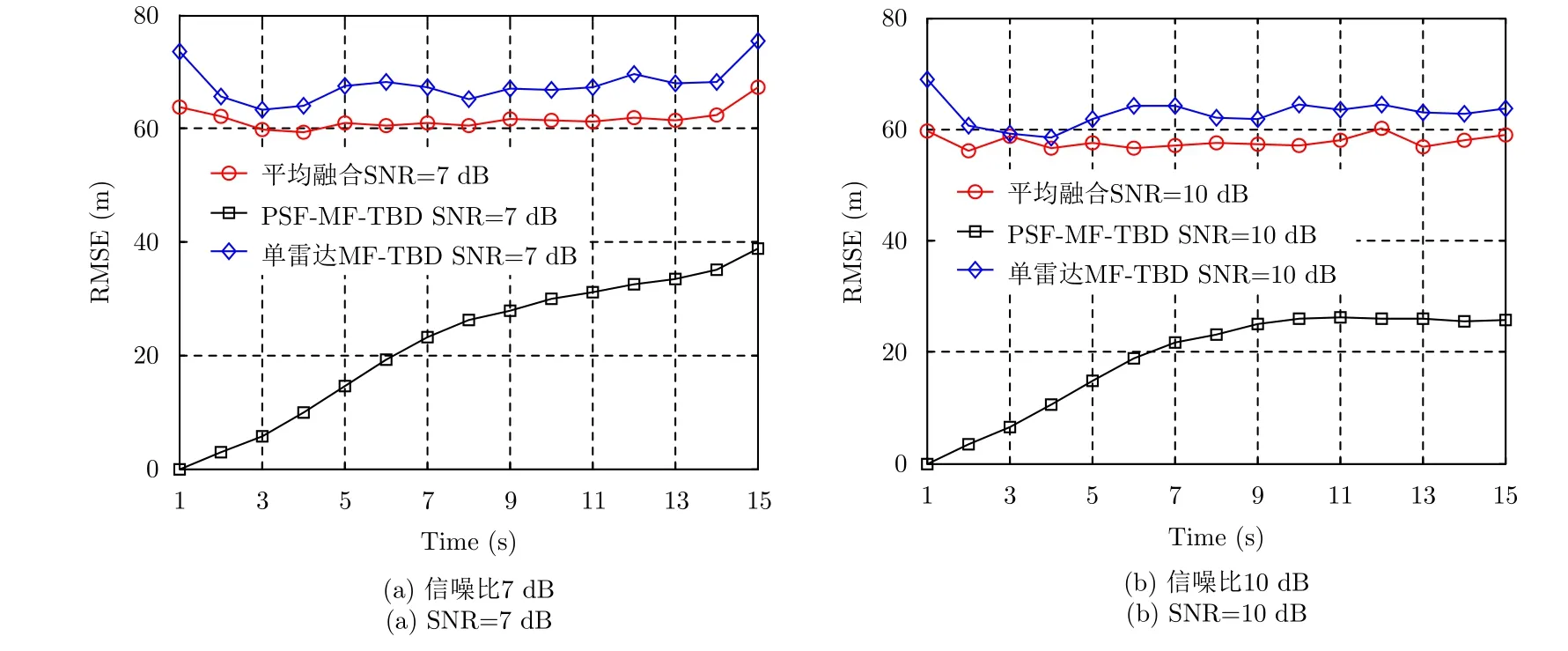
图9 不同点迹序列融合方法的RMSE对比Fig. 9 RMSE of different plot sequence fusion methods