基于EASI盲分离算法的雷达抗相参干扰方法

许佳奇，于 涛，姜 芳

(中国洛阳电子装备试验中心，河南 洛阳 471000)

0 引言

脉冲压缩雷达抗干扰性能的本质是干扰信号与雷达信号不相参，在雷达做脉压处理时不能得到相应的脉压增益[1-2]。因此干扰信号要尽可能保证与雷达信号的相参性，才能对脉冲压缩雷达产生较好的干扰效果。相参干扰是采用数字射频存储(DRFM) 技术[3-4]，将侦收到的雷达信号进行存储，然后进行一定的调制后再将其转发，雷达接收到干扰信号后经过脉压处理能获得较高的脉压得益，对雷达形成假目标欺骗或压制的效果。间歇采样干扰是相参干扰中最典型的一种干扰方式，对雷达信号切片后转发，产生的假目标干扰信号与雷达信号有很强的相参性[5-6]。

盲源分离(BSS)算法是指从混合信号中提取、分离出源信号的技术[7-8]，它的研究起步于20世纪80年代，并逐渐发展成为一种实用性很强的信号处理方法。根据寻优方法的不同，盲源分离算法可分为两类：一类是基于高阶统计的方法，代表性的有固定点算法(FastICA)、联合对角化算法(JADE)等；另一类是基于代价函数最优化的方法，代表性的有基于独立性的等变自适应分离算法(EASI)、自然梯度法算法(NGA)等。目前，基于高阶统计的盲源分离方法在雷达抗相参干扰中得到了一定的研究，文献[9]首次利用JADE算法实现了脉冲压缩雷达抗主瓣压制干扰；文献[10]利用FastICA算法实现了目标回波信号与压制干扰信号的分离。然而基于代价函数最优化的盲分离算法在雷达抗相参干扰中的研究还较少。

本文首先给出了间歇采样干扰的原理，提出了利用独立等变自适应分离算法(EASI)分离雷达接收到的目标回波与干扰信号的混合信号，然后将分离信号经过脉压处理，找到目标信息从而实现抗干扰。仿真实验表明，EASI盲分离算法对间歇采样转发干扰的干扰抑制比能达到20 dB，有效降低了相参干扰对脉冲压缩雷达探测性能的影响。

1 问题描述

根据干扰机的收发体制，相参干扰可以分为收发同时干扰和收发分时干扰，其中收发同时干扰由于对干扰机收发天线的隔离度有很高的要求，工程实现较为困难。收发分时干扰最典型的干扰样式为间歇采样转发。

设雷达发射信号为线性调频信号：

s(t)=rect(t/T)exp(j2π(f0t+kt2/2))

(1)

式中，f0为雷达信号中心频率，B为信号带宽，T为信号脉宽，k=B/T为调频斜率。

s(t)经过匹配滤波器的脉压输出为：

y(t)=rect(t/(2T))Tsinc(kπtT)exp(j2πf0t)

(2)

间歇采样干扰的时序关系如图1所示，干扰机侦收到雷达脉冲信号后，对其进行周期为Ts的等间隔采样，接收时间窗为τ，将其存储后放大转发，采样与转发交替进行直到雷达脉冲信号结束。

图1 间歇采样干扰时序

间歇采样干扰信号与雷达发射信号的关系为：

(3)

干扰信号经过匹配滤波器后的脉压输出为：

(4)

式中，fs=1/Ts是间歇采样重频。

由式(4)可知，间歇采样干扰信号的脉压增益较大，有较强的相参性。

如图2所示，源信号为目标回波信号s(t)和干扰信号J(t)，源信号在传播及被传感器接收过程中会产生信号混叠，加上噪声后构成了雷达接收到的混合信号x(t)。为了保证混合信号的可分离性，至少需要2个接收天线。因为噪声对脉冲压缩雷达的影响较小，所以将其忽略后混合信号可表示为：

(5)

式中，只有雷达接收到的混合信号x(t)为已知。

图2 线性瞬时混叠盲源分离模型

EASI盲分离算法的目的就是找到混合信号x(t)的一个分离矩阵W，使得其输出的分离信号z(t)最大限度逼近源信号s(t)和J(t)，即：

(6)

2 EASI盲分离算法

Cardoso将白化处理和盲分离算法相结合，提出了EASI 算法[11]，其分离过程主要分为两个步骤，第一步是对混合信号进行白化预处理，消除混合信号之间的相关性，降低问题的复杂度；第二步是设定目标函数，通过优化算法对分离矩阵进行迭代更新，使分离信号最大限度地逼近源信号。

白化预处理是将混合信号作线性变换，使其变成自相关矩阵为单位阵、信号各分量具有单位方差且互不相关的白色信号。对混合信号x(t)进行白化预处理，得到：

(7)

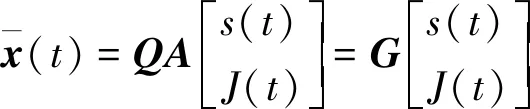
(8)

(9)

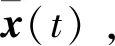
梯度法是求目标函数最值问题的典型方法，首先设定一个初始的分离矩阵W0，计算目标函数在W0处的梯度，然后沿此方向移动一个合适的步长得到新的分离矩阵W1，重复上述过程可得到W的迭代公式：

W(k+1)=W(k)+ΔW

(10)

式中，ΔW=α(k)∂L(W(k),z)/∂W(k)，k为迭代次数，α(k)为步长。

构建基于互信息最小化的目标函数L(W,z)，设分离信号z的概率密度函数为pz(z)，各分量的概率密度函数为pzi(zi)，各分量间统计独立性的互信息为：

(11)

(12)

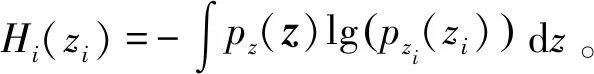
由于H(x)对W求梯度时为零，可以从式(12)中删除，得到目标函数：

(13)

目标函数对分离矩阵求得随机梯度为：

L(W,z)=∂L(W,z)/∂W=-W-T+E(φ(z)xT)

(14)

(15)

将其代入迭代公式，可得自然梯度的迭代公式为：

W(k+1)=W(k)+α(k)(-I+E(φ(z)zT))W(k)

(16)

结合白化过程，可得EASI的迭代公式为：

W(k+1)=W(k)+α(k)(-2I+E(zzT)+

E(φ(z)zT))W(k)

(17)

3 仿真实验与分析

仿真中，设雷达接收的混合信号包含了目标回波信号、间歇采样干扰信号以及噪声。其中目标回波信号为线性调频信号，其采样率为5 kHz，脉宽5 μs，带宽100 MHz；干扰信号的间歇采样周期为0.5 μs，采样转发比为1∶4；噪声为高斯白噪声。

为了定量评价EASI盲分离算法的抗相参干扰效果，本文采用干信比ISR作为评价指标。令信噪比为恒定值，SNR=0 dB，ISR从0 dB逐渐提升到40 dB，观察混合信号与分离信号进行脉压处理的结果。当ISR=13 dB时，如图3所示，图3(a)是混合信号的脉压结果，最左侧的尖峰为目标信号，其余4组尖峰为间歇采样干扰信号，每组的干扰信号又包含了第一假目标、第二假目标等信号，峰值依次降低。可见此时的干扰信号第一假目标峰值与目标信号峰值接近，间歇采样干扰起到了很好的假目标欺骗作用。图3(b) 是采用EASI盲分离算法后得到的目标分离信号的脉压结果，可见只在目标处有一个非常明显的脉压尖峰，EASI盲分离算法起到了很好的干扰抑制作用。

图3 ISR=13 dB的脉压结果

当ISR=33 dB时，如图4所示，图4(a)中混合信号的脉压结果有明显的4组干扰信号，而目标信号已经被淹没。图4(b)中经过EASI盲分离处理后的分离信号的脉压结果还能看到目标信息，其峰值与干扰信号脉压峰值接近。

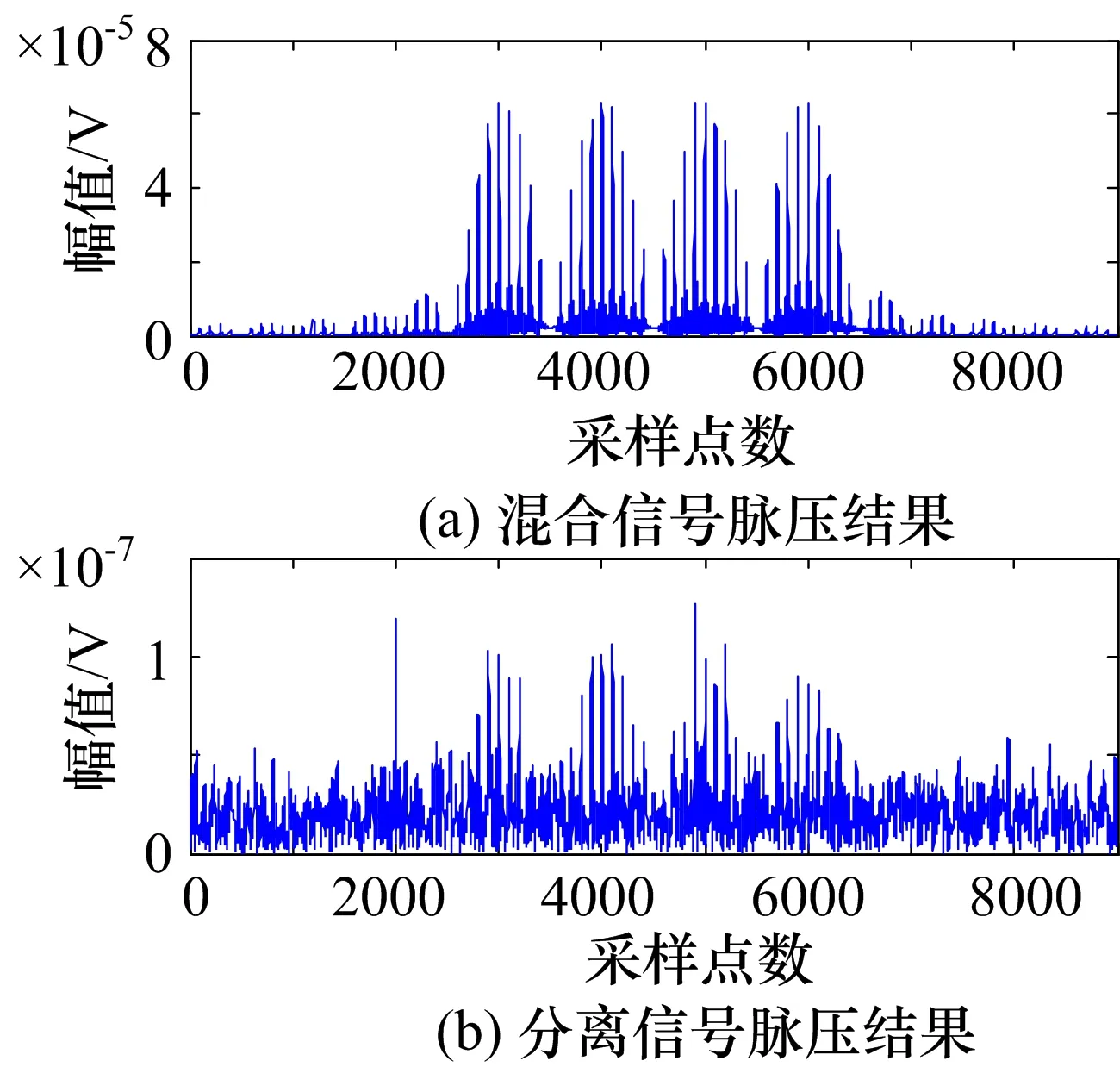
图4 ISR=33 dB的脉压结果

通过图3(a)与图4(b)脉压结果的对比，可见在SNR为恒定的0 dB的条件下，在采用EASI盲分离算法后，间歇采样干扰被抑制了20 dB，从而证明了EASI盲分离算法对相参干扰具有良好的抑制能力。

4 结束语

针对脉冲压缩雷达抗相参干扰能力弱的问题，本文提出了利用EASI盲分离算法抗相参干扰。该方法能有效提升脉冲压缩雷达在复杂相参干扰环境下对目标的检测能力。仿真实验表明，在信噪比为0 dB的条件下，利用EASI盲分离算法处理后的脉压结果对间歇采样干扰的抑制比能达到20 dB，有效降低了相参干扰对脉冲压缩雷达探测性能的影响，具有良好的应用前景。