基于MC方法总工期风险问题研究

吴雪玉　唐根丽

[提要] 为准确预测工期，降低工程项目风险，可通过蒙特卡洛方法研究工程工期风险问题。首先确定工期概率分布类型为贝塔分布，继而利用线性同余法生成伪随机数，选定模拟次数N为1000，利用概率统计理论对模拟结果分析，得出在一定完工概率情况下的工期。将模型应用到具体工程项目案例，通过分析项目各工序之间的逻辑关系，得到四条线路，每一条线路对应的时长分别为：线路1-1168天，线路2-1059天，线路3-1152天，线路4-1253天。工期取MAX（线路i，i=1，2，3，4）=1253天，假设完工概率不小于80%为合理工期，利用Crystal Ball进行分析得此工程项目的合理工期是1110（1109.42）天。由此可见，将该模型应用到其他工程项目可使承包商对项目的定位更准确，得到最优化决策。

关键词：工期风险;蒙特卡洛;工期预测;Crystal Ball

中图分类号：TU722 文献标识码：A

收录日期：2019年5月9日

在建筑工程项目管理中，工期是项目目标控制的三大关键环节之一。在项目实施过程中，存在多种风险，这对项目按时完成造成巨大的威胁。工期风险一般根据概率进行估计，通常用不能按计划工期完工的概率来表示。一个项目的工期计算是从破土施工到竣工验收整个过程所需的全部时间，工期预测不准确带来的损失较大。本文通过建立蒙特卡洛方法研究工程工期风险问题，利用概率统计理论对模拟结果分析，得出在一定完工概率情况下的工期，这样才能对工期风险有效预估以及把握整体工期，这对于项目工期管理水平的提升具有重要意义。

一、工期风险主要分类

一般情况下，工程项目的工期风险主要包括五个因素，分别是：自然环境因素、项目所在地的气候、项目运行时的特殊天气以及该地区的地质等条件均会在一定程度上影响工程工期;承包商因素，承包商的业务处理方式如果存在施工调度不当和项目分包不当等情况会严重拖慢项目整体进度;业主因素，业主设计变更和监管不严也会使进度拖后;设计方因素，业主提出设计变更后设计方不能及时给出最新图纸以及技术方案不当等对工程工期也会造成拖延;社会经济因素，国家进行宏观调控提出的一些针对工程问题的政策以及某些特殊规定都会在一定程度上影响项目工期等其他因素。详细分类情况如图1所示。（图1）

二、蒙特卡洛方法概述

蒙特卡罗方法又称统计模拟方法，是20世纪40年代中期顺应科学技术的发展和电子计算机的发明提出的以概率统计为理论支撑的数值计算方法。它是指使用随机数（或伪随机数）来解决许多计算问题的一种办法。而蒙特卡罗方法正是以概率为基础的方法，与它对应的是确定性算法。

MC方法通过构造模拟客观事物间的逻辑关系和实际过程，利用计算机进行模拟，从而得到研究对象发生的概率以及可能带来的损失值。使用MC方法具有如下优点：它只要求风险事件概率能准确地用数学式来描述就能得到解，且在计算机上的模拟次数足够多时，其解的精度就会较高;整个模拟过程中不依赖人的主观评判，结果较为客观;其方法和程序也较简单，且此方法的思路明确，易实现。其缺点有：MC方法仅是一种数值计算方法，本身并不能对对象进行优化，如果想要得到满意解或最优解时，就需要进行大量模拟，具有與枚举法类似的缺点，同时多次模拟需要做一系列的重复运算，就会占用较多的计算机内存，且耗费时间;MC法是通过建立数学模型确定各变量之间的数值关系并在计算机上进行大量试验来模拟其最终解，因此它不能给出过程解和中间成果，比如在进行工期风险模拟时，我们只能最终得到总工期概率分布的参数，不能得到每项工作详细的时间参数。但这些缺点会因计算机技术的发展不断得到改善，本文计算工程项目的工期风险，主要分析总工期概率分布及时间参数，因此本文采用MC法是可取的。

三、蒙特卡洛模型解工期风险问题

MC方法的基本原理就是利用计算机进行大量的模拟试验，对其结果进行统计和分析。本文用此方法进行工期风险分析也有与其类似的原理。在进行模拟工期实验时，我们首先要确定网络计划的工序持续时间所服从的分布函数，再通过随机抽样，得到工程项目每一工序持续时间的随机数，通过随机数得到的持续时间进行计算得到网络计划的总工期和关键线路。重复进行N次后，对统计结果进行数理分析，然后统计可能的关键线路的期望和方差，进而运用概率统计等相关知识计算工程项目在规定工期下的完工概率或进度风险。

（一）确定工期的概率分布类型。本文以贝塔分布进行工期风险问题研究。我们假设工期的概率分布是贝塔分布，它是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数，同时在机器学习和数理统计学中均有重要应用。在概率论中，贝塔分布，也称Β分布，是指一组定义在（0，1）区间的连续概率分布，有两个参数α、β。

（三）确定模拟次数。与蒙特卡洛对应的模拟软件一般情况下采用Excel的插件Crystal Ball或者MATLAB，本文使用前者。通常Crystal Ball默认模拟次数是1，000，随着模拟次数的增多，模拟得到的结果也就越准确，得到的工期完成率等各类指标可信度也会提高。本文选取模拟次数N=1000。

（四）获得统计数据。用三时估计法估计最乐观时间a，正常时间m，最悲观时间b。

（五）运行模拟得出统计参数并分析。重复操作N次产生伪随机数与统计样本统计值，通过概率统计分析，从而估计其参数，即在某特定概率下工期的可能值。

四、工程项目案例应用

某工程项目包含基坑支护，各类装修与安装工序，直到竣工验收的全过程，工序11塔楼室外装修与安装的时间间隔为26天。根据项目各工序紧前工作等信息经计算可得三时估计表如表1所示。（表1）

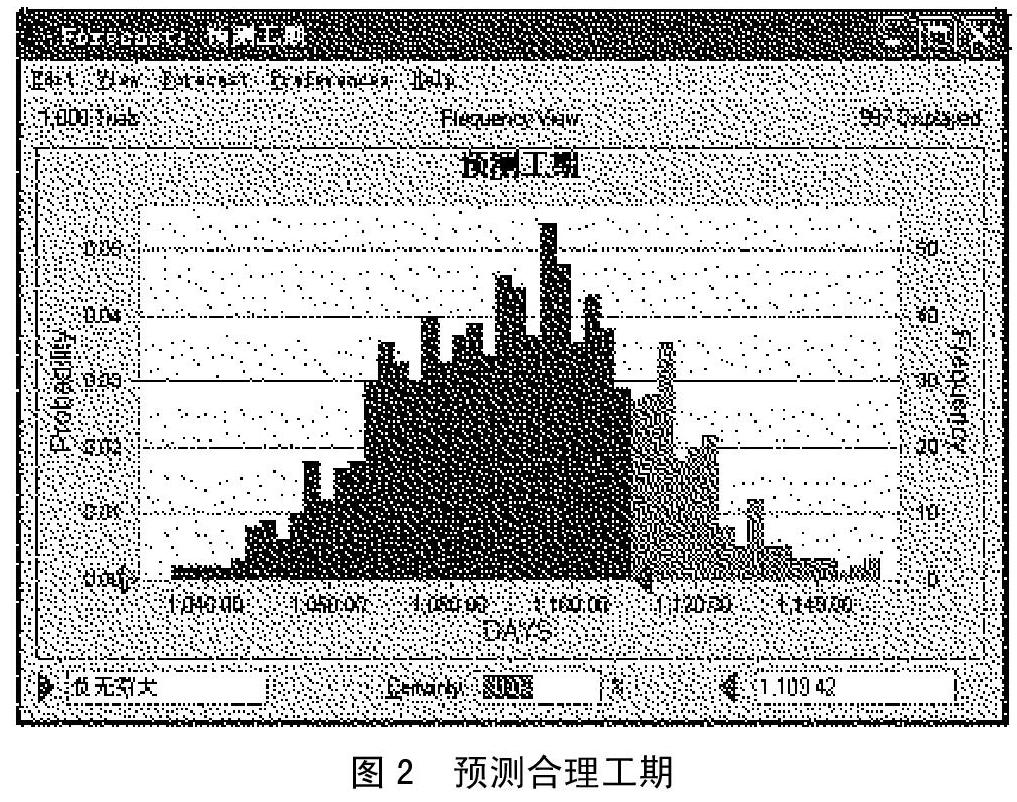
通过分析项目的各工序之间的逻辑关系，得到四条线路，每一条线路对应的时长分别为：线路1-1168天，线路2-1059天，线路3-1152天，线路4-1253天。工期应取MAX（线路1，线路2，线路3，线路4）=1253天，故工期模拟模型所得工期是1，253天。设在完工概率不小于80%为合理工期，在此状态下此工程项目的合理工期是1，110（1，109.42）天。运行结果如图2所示。（图2）

五、工程工期风险预测和控制措施

针对以上分析，显然蒙特卡洛方法在数值模拟方面对工期的预测具有很大的帮助，这对于准确把握工程项目进度具有重要意义。当然，本文也有部分考虑不全面的地方，在工程工序持续时间分布的确定时，文中是假设其服从贝塔分布，实际情况肯定有一定偏差。具体改进方法還需要继续研究。

同时，联系工程实际，针对影响工程工期的不同风险，我们提出了一些针对工程工期风险预测和控制的一些具体措施。可以控制施工过程中影响较大的不确定性因素。

（一）进行项目人员专业培训。在工程项目的进行过程中，施工人员的流动性较大，对于所有的施工人员都要事先进行一定的实践培训，以免对工程项目整体进度产生影响，对其他所有参与工程项目的人员也都要进行专业培训，工作人员对业务的熟悉与否对项目的某个工序都或多或少会有一定影响，因此必要的岗前培训对项目的顺利进行是有益的。

（二）不定期对项目进度抽查记录。一般大型工程项目，项目现场人员数量多且部门复杂，管理人员如果没有合理安排所有人员的具体工作，很有可能就会出现人员冗余的情况，浪费企业资源。为此，企业需要做好监督工作，对工程项目进度不定期进行抽查，针对具体工序做出不同的督促工作。如果该工序正常完成计划进度或者超前完成计划进度，此时该项目就可以延续之前的施工控制;相反，如果该工序已经超出计划工期范围并且还未完成，同时项目逾期的赔偿金是承包商不能担负的，此时就要考虑对该工序采取加急措施，加大工作量，赶工完成，直到后面的项目赶上计划工期再恢复之前的工作进度。

（三）工程技术完善。由于工程项目实施过程中机器设备老化、损坏使得工程项目的整体进度拖后，承包商就要针对自身情况进行设备的更换或者技术方面的改进，使得项目可以在计划工期内完成。

（四）反馈机制完善。反馈机制对于项目的促进作用是显然的，监管人员在发现工程项目进行过程中存在任何有可能会延误工程项目进度的事件均要及时上报，并积极沟通完成两者对接，使得解决方案可以及时传达给对应工序的工作人员，在保证施工场地安全情况下力求在最短的时间内完成方案的纠正。

（五）分阶段激励。在工程项目的各个阶段完成以后，可以采取一定的物质或精神奖励以激励员工在后面工序的积极性，避免长时间的工作强度下人会产生消极情绪降低工作效率的现象发生。在分阶段激励机制下，人们会有积极性继续进行下一步工作，可以保证工程项目工期进度。

主要参考文献：

[1]陈小文.建筑工程施工风险影响因素分析与评价研究[D].浙江大学，2017.

[2]任琼琼.基于风险因素自相关性的施工进度风险分析研究[D].南昌航空大学，2017.

[3]李东亮.基于MCS和PERT的引水工程工期风险分析[J].黄河水利职业技术学院学报，2017.29（2）.

[4]武菲菲，王学海，程铁信.基于PERT的多因素影响下的项目工期风险评价[J].工业工程，2015.18（6）.

[5]武菲菲.基于PERT的项目工期风险评价与动态控制研究[D].天津工业大学，2016.

[6]项勇，任宏.工程项目工期风险因素影响分析——基于贝叶斯网络理论和非叠加原理[J].技术经济与管理研究，2015（2）.

[7]王丹净.蒙特卡洛法在建筑工程项目管理中的应用及影响[J].财经问题研究，2014（S2）.

[8]郭琦，何金静，胡苗.基于蒙特卡洛模拟的工程项目网络计划进度风险分析[J].项目管理技术，2013.11（11）.