中小学生人群聚集处不安全行为倾向研究

杨新宇,郭明乐

(中国地质大学(武汉) 工程学院，湖北 武汉 430074)

当前，我国中小学正进入安全事故多发期。据联合国统计，我国每年因意外伤害而死亡的儿童超过20万人，平均每天有540多名儿童因意外伤害而死亡，儿童因意外伤害死亡的人数占儿童总死亡人数的1/3，学校的安全工作形势十分严峻。因此，加强中小学学生行为管理及其学校周边环境的研究，并针对学生不安全行为的倾向与特点采取有效的控制对策已成为当前不容忽视的问题。

目前国内外学者在人群行为领域的研究主要集中在人群行为特征、行为干预、行为模型、行为异常检测和人员疏散等方面。如在人群行为特征分析方面，刘洵[1]从心理学、社会学和生物学的角度出发，基于行为科学的基本原理，通过数据统计分析、现场观察和文献调研等方法分析了人群在普通状态和紧急状态下的行为特征，并对影响人群行为的内外因素进行了系统的归纳，进而提出了干预措施；吴宦漳等[2]研究了寒地城市广场人群行为模式及其影响因素，并以哈尔滨市建筑艺术广场为研究对象，运用实地调研和统计分析等方法确定出不同时间段内人群数量的变化规律和人群活动时间的规律；张朋跃[3]通过人群状态分析与异常行为检测研究，根据人群聚散过程中表现出的行为特征，利用数学建模的方法，提出了一种基于网格单元特征的人群聚散行为分析模型；席文波[4]通过公共场合旁观人群行为的现象学研究，以“公共交通工具上让不让座”这一热点问题为例，运用现象学的科学研究方法分析了公共场合旁观人群行为的本质；孙金龙等[5]为了研究人群恐慌状态对地铁应急疏散的影响，分析了地铁应急疏散过程中人群恐慌状态下的行为特征及其影响因素，构建了恐慌条件下人群疏散模型，并将此模型运用Anylogic软件进行了仿真模拟；杨洁等[6]采用网络问卷的方式，对大型商场内人群择路行为认知规律进行了研究；崇信毅[7]基于视频监控获得的人群运动轨迹数据集， 建立了人群行为分析的完整框架。在不安全行为控制方面，如姚庆国等[8]为了探究沟通满意度对煤矿矿工不安全行为的影响，通过对239份有效问卷调查数据进行统计与分析,基于SEM理论构建了矿工不安全行为与沟通满意度的关系模型；袁斌[9]基于相关不安全行为管理理论，构建了不安全行为管理模型，通过对某化工集团某工厂8个工种工人的生产作业过程进行为期6个月的跟踪观察，收集并统计了工人生产作业过程中的不安全行为，并分类整理出工人各种类型不安全行为总量的变化趋势及所占的比例，从而验证了不安全行为管理方法对化工生产过程中控制工人不安全行为的有效性及其效果。20世纪末期，智能监控对人群异常行为的识别与分析已经得到广泛的应用。美国国防高级研究计划局(DARPA)资助的HID(Human Identification at a Distance)计划[10]，主要利用生物识别等相关技术对远距离条件下的行人进行检测与识别；Wu等[11]利用光流法提取人群运动信息，采用局部聚类的方法获得具有代表性的人群运动轨迹，并通过引入混沌动力学的概念提取了复杂人群运动的一组混沌特征，进而判断人群是否会出现异常情况；Mehran等[12]将流体力学中的脉线扩展到人群异常行为的识别中，利用人群稳定与不稳定时截然不同的脉线表示方式来识别人群的异常行为；Adam等[13]设计了基于低水平统计学特征的多重并联的人群异常情况监视器，用来识别特定的异常行为。在人群行为模型方面，Reynolds[14]通过对群体的自主行为加以阐述，在运用分布式行为体系对鸟群、鱼群进行仿真模拟的基础上，建立了人群行为模型[14]。

以上研究主要针对的是密集人群在公共空间的行为特征，均有助于对人群行为倾向性的把握，但整体上看人群特点并不突出，尚未有针对中小学生群体的行为研究。中小学生群体具有自身的行为特点，主要表现为缺乏自我保护能力，生活经验不足，对事物的辨别能力弱，缺乏对致害因素的警惕性，且好动、好奇，理解能力和判断能力较差，加上心理承受能力欠缺，当遭遇紧急、危险情况时往往缺乏正确的判断而惊慌失措，因此容易遭受各种意外的伤害，成为受害者。鉴于此，本文基于某附属学校上放学前后学校大门口处的监控视频，通过统计与分析相关数据，以期得出中小学生人群聚集处不安全行为倾向的规律性结果，为预防中小学生在公共场所的安全事故提供依据。

1 研究方法

1. 1 数据获取方法

本文采用统计监控视频数据与实地调查相结合的方法，根据调查内容选择学校大门处的监控视频获取中小学生人群的活动数据，视频截取的时间段是早、中、晚上学及放学时学生流量高峰期，调查时间为工作日，天气情况包含晴天和雨天。

1. 2 统计量的选取

1.2.1 刻画集中趋势的描述统计量

集中趋势是指一组数据向某个中心值靠拢的倾向。计算集中趋势的描述统计量正是要寻找到能反映数据一般水平的“代表值”或“中心值”，本文选取的刻画集中趋势的描述统计量为均值。

设观测变量的值有n个，记为X1，X2，…，Xn,则算术均值为

(1)

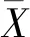
1.2.2 刻画离散程度的描述统计量

离散程度是指一组数据远离其中心值的程度。本文选取刻画离散程度的描述统计量主要为标准偏差、偏斜度、峰度。

标准偏差S的计算公式为

(2)

式中：S为数据的标准偏差(无量纲)。

偏斜度是用来描述变量取值分布的偏斜方向，用以衡量分布对称与否以及分布不对称的方向和程度。偏斜度α的计算公式为

(3)

式中：α为数据的偏斜度(无量纲)；S为数据的标准偏差(无量纲)。

峰度是用来描述变量取值分布形态的陡缓程度，即描述分布图形的尖峭程度或峰凸程度。峰度β的计算公式为

(4)

式中：β为数据的峰度(无量纲)；S为数据的标准偏差(无量纲)。

1. 3 调查因子的选取

根据监控视频的观察和中小学生在学校大门口处人群聚集情况的特点，本文选取人群密度和人群聚集度作为调查因子[15]进行分析。

人群密度的计算公式为

D=(QM+QS)/A

(5)

式中：D为人群密度(人/m2);QM为路段上移动人流量(人/min)；QS为路段上停留人流量(人/min)；A为路段的面积(m2)。

本文以人群聚集点密度、影响范围、聚集持续时间为评价标准，构建了如下人群聚集度计算模型：

(6)

式中：G为路段上人群聚集度(人·min)；Di为路段上第i个聚集点的人群密度(人/m2)；Fi为路段上第i个聚集点的人群聚集影响范围(m2)；Ti为路段上第i个聚集点的人群聚集持续时间(min)；m为路段上人群聚集点的个数(个)。

1. 4 数据间相关关系的卡方检验

卡方检验(Chi-square test)也称为卡方拟合优度检验(Chi-square goodness-of-fit test)，主要用于检验样本数据是否与某种概率分布的理论数值相符合，进而推断样本数据是否来自于服从某概率分布的总体。

卡方检验的零假设是：总体χ服从某种概率分布，这里的样本认为是来自于服从某种概率分布的总体χ。卡方检验的基本原理是在给定的零假设条件下，根据样本值落在总体χ的各个区间的频数与总体落在该区间的期望频数的差值，构造服从卡方分布的Pearson统计量。具体而言，将总体χ分成k个不相交的区间(子集)，如果样本值落在总体的第i个区间的频数为ni,则卡方统计量χ2近似服从自由度为k-1的卡方分布:

(7)

式中：n为样本总数，这里指人数；pi为总体落在第i个区间的概率值;npi为期望频数;k为不相交区间(子集)的分割数量，k应足够大。

从卡方统计量χ2的计算公式可以看出:如果χ2值较大，则样本频率分布与期望频数分布差距较大；反之，如果χ2值较小，则样本频率分布与期望频数分布较接近。

SPSS软件将自动计算卡方统计量的观测值，并依据卡方分布表计算观测值对应的频率p值。如果χ2的概率p值小于显著性水平，则应拒绝零假设，认为样本不是来自于服从某概率分布的总体；反之，如果χ2的概率p值大于显著性水平，则不能拒绝零假设，认为样本来自于服从某概率分布的总体。

2 中小学生不安全行为的实证分析

本次调查样本选自中国地质大学(武汉)附属学校大门口处的监控视频数据,该附属学校由附属中学、附属小学及附属幼儿园组成，因附属幼儿园处于较远的一个独立校区，且幼儿不属于本次的研究对象，故本文只针对附属中学、附属小学校区进行研究。全校设有35个教学班，在校学生约1 500人，符合本文研究对象的要求。

2. 1 中小学生不安全行为的描述统计分析

本次调查选用学校大门口处的监控视频数据进行描述统计，共统计了10 d内4个时间段(7∶45—7∶55、12∶00—12∶10、13∶35—13∶45、16∶45—16∶55)中小学生人群活动的相关数据，其中包括各个时间段内通过校门口的中小学生总人数、男女生人数、主要不安全行为种类、各种类不安全行为的人数及男女生比等数据，并建立了中小学生不安全行为监控视频调查数据表并进行了统计分析，详见表1和表2。

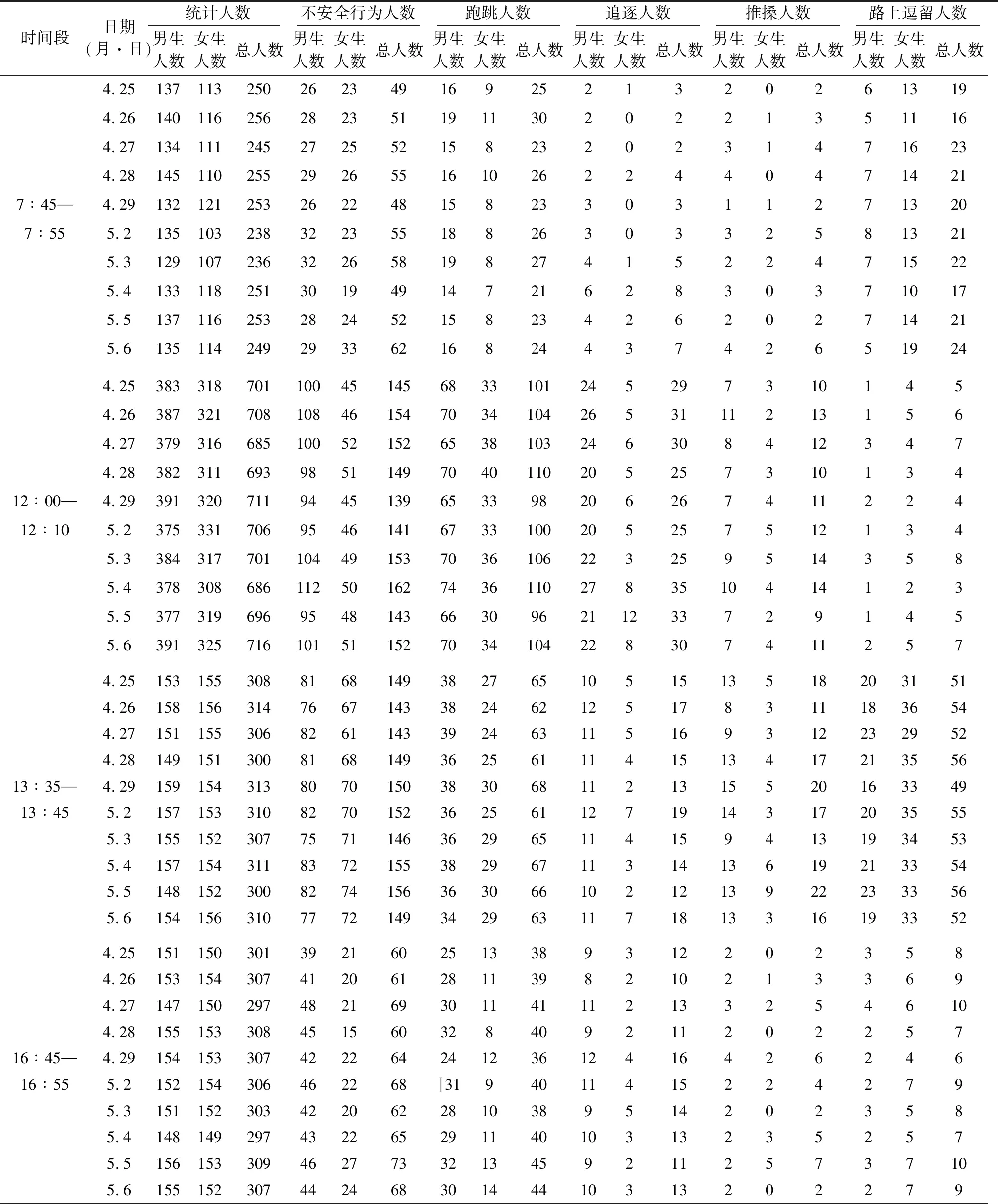
表1 中小学生不安全行为监控视频调查数据表(单位：人)

表2 中小学生不安全行为监控视频调查数据统计分析结果

(1) 早上7∶45—7∶55时间段内中小学生不安全行为数据的描述统计:对学校大门口处10 d内早上7∶45—7∶55时间段的中小学生不安全行为数据进行整理，并计算其平均值、标准偏差、偏斜度、峰度。

早上学生上学高峰期内，每十分钟通过学校门口的中小学生人流量约249人，标准偏差S为6.883，偏斜度α为-1.015，峰度β为-0.113,人数分布基本符合正态分布；男生人数为136人，女生人数为113人；中小学生不安全行为的人数为53人，占总人数的21.4%，其中男生出现不安全行为的人数为29人，占男生总人数的21.4%，女生出现不安全行为的人数为24人，占女生总人数的21.2%。

另外，在早上7∶45—7∶55时间段内中小学生有跑跳、追逐、推搡、路上逗留4种主要不安全行为的统计结果，见图1。

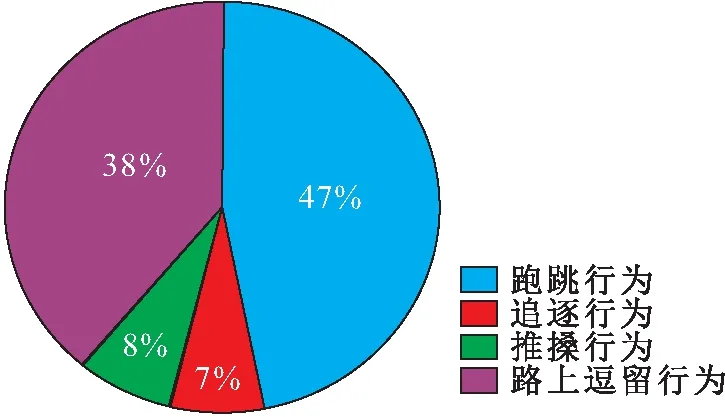
图1 早上7∶45—7∶55时间段内中小学生4种主要 不安全行为统计图Fig.1 Statistical graph of four main unsafe behaviors of primary and middle school students in the period of 7∶45—7∶55

由图1和表2可见，跑跳和路上逗留是早上上学期间易发生的主要不安全行为，分别占38%、47%，其中有跑跳行为的男女生比是163∶85，约等于2∶1；有路上逗留行为的男女生比是11∶23,约等于1∶2。

(2) 中午12∶00—12∶10时间段内中小学生不安全行为数据的描述统计：对学校大门口处10 d内中午12∶00—12∶10时间段的中小学生不安全行为数据进行整理，并计算其平均值、标准偏差、偏斜度、峰度。

中午学生放学期间即12∶00—12∶10时间段内，每十分钟通过学校门口的中小学生人流量约为700人，标准偏差S为1.273，偏斜度α为-0.115，峰度β为-0.949，人数分布左偏，基本符合正态分布；男生人数为383人，女生人数为319人；中小学生不安全行为的人数为149人，占总人数的21.3%，其中男生出现不安全行为的人数为101人，占男生总人数的26.4%，女生出现不安全行为的人数为48人，占女生总人数的25.1%。

另外，在中午12∶00—12∶10时间段内中小学生有跑跳、追逐、推搡、路上逗留4种主要不安全行为的统计结果，见图2。

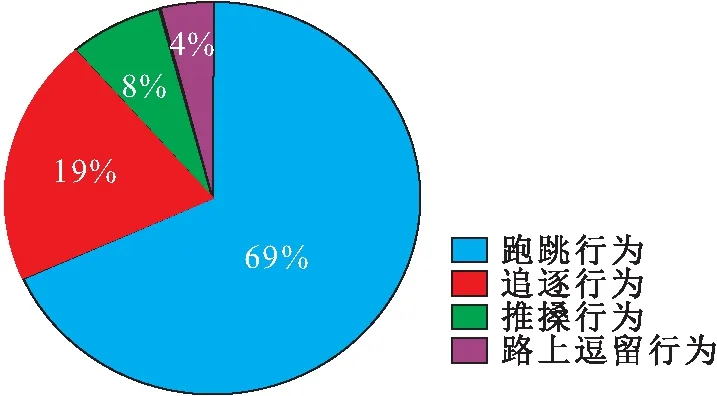
图2 中午12∶00—12∶10时间段内中小学生4种主要 不安全行为统计图Fig.2 Statistical graph of four main unsafe behaviors of primary and middle school students in the period of 12∶00—12∶10

由图2和表2可见，跑跳和追逐是中午放学期间的主要不安全行为，共占比为88%，其中有跑跳行为的男生约有68人，有跑跳行为的女生约有35人，男女生比约为2∶1；追逐行为中，男生有23人，女生有6人，男女生比约为4∶1；推搡和路上逗留行为在中午放学期间发生的概率相对较低，推搡行为人数共有12人，其中男生有8人，女生有4人，男女生比约为2∶1，路上逗留行为人数共有6人，其中男生2人，女生4人，男女生比为1∶2。

(3) 下午13∶35—13∶45时间段内中小学生不安全行为数据的描述统计：对学校大门口处10 d内下午13∶35—13∶45时间段的中小学生不安全行为数据进行整理，并计算其平均值、标准偏差、偏斜度、峰度。

下午学生上学期间即13∶35—13∶45时间段内，每十分钟通过学校门口的中小学生人流量约为308人，标准偏差S为2.883，偏斜度α为-1.015，峰度β为-0.113，人数分布左偏，基本符合正态分布；男生人数约为154人，女生人数约为154人；中小学生不安全行为的人数约为149人，占总人数的48.4%，其中男生出现不安全行为的人数约为80人，占男生总人数的51.9%，女生出现不安全行为的人数为69人，占女生总人数的44.8%。

另外，下午13∶35—13∶45时间段内中小学生有跑跳、追逐、推搡、路上逗留4种主要不安全行为的统计结果，见图3。

图3 下午13∶35—13∶45时间段内中小学生4种主要 不安全行为统计图Fig.3 Statistical graph of four main unsafe behaviors of primary and middle school students in the period of 13∶35—13∶45

由图3和表2可见,下午上学时间段内中小学生有在学校门口聚集的习惯，对比分析早7∶45—7∶55时间段中小学生的不安全行为，路上逗留这种不安全行为所占的比例在两个时间段均达到了38%，明显高于放学的两个时间段；中午放学时间段12∶00—12∶10内，该行为所占的比例仅为4%；而逗留在学校门口的中小学生喜欢进行跑跳、追逐、推搡等不安全行为，统计各种不安全行为的男女生比，跑跳行为的男女生比约为2∶1,追逐行为的男女生比约为3∶1，推搡行为的男女生比约为3∶1，路上逗留行为的男女生比约为1∶2。

(4) 下午16∶45—16∶55时间段内中小学生不安全行为数据的描述统计：对学校大门口处10 d内下午16∶45—16∶55时间段的中小学生不安全行为数据进行整理，并计算其平均值、标准偏差、偏斜度、峰度。

下午学生放学期间即16∶45—16∶55时间段内，学校门口每十分钟通过的中小学生人流量约为304人，标准偏差S为1.467，偏斜度α为-0.847，峰度β为-0.832，人数分布左偏，基本符合正态分布；男生、女生人数均为152人；中小学生不安全行为的人数为65人，占总人数的21.4%，其中男生出现不安全行为的人数为44人，占男生总人数的28%，女生出现不安全行为的人数为21人，占女生总人数的13.8%。

另外，下午16∶45—16∶55时间段内中小学生有跑跳、追逐、推搡、路上逗留4种主要不安全行为的统计结果，见图4。

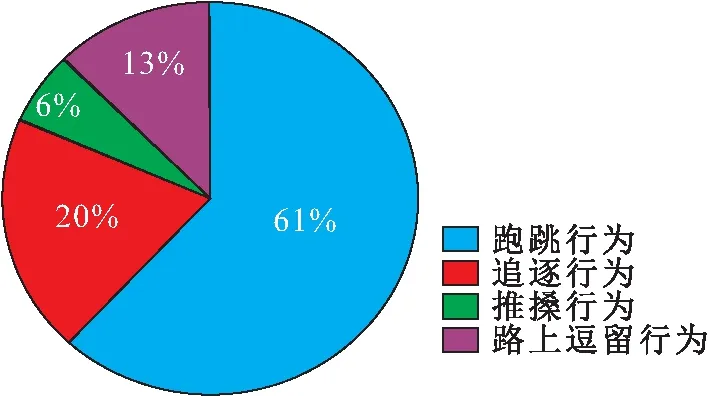
图4 下午16∶45—16∶55时间段内中小学生4种主要 不安全行为统计图Fig.4 Statistical graph of four main unsafe behaviors of primary and middle school students in the period of 16∶45—16∶55

由图4和表2可见，跑跳、追逐、路上逗留是晚上放学阶段内中小学生的主要不安全行为，占比分别为61%、20%、13%。

通过分析学校大门口处10 d四个时段内中小学生的不安全行为，可以粗略地做出如下推断：男生发生不安全行为的概率要高于女生；4种不安全行为中，男生易于发生跑跳、追逐、推搡行为，女生易于发生路上逗留行为；4个时间段内中小学生不安全行为发生的概率基本相同，概率分别为21.4%、21.3%、21.3%、21.4%，均值为21.35%，即每5名中小学生中约有1名可能发生不安全行为；不同时间段内中小学生发生的不安全行为有不同的倾向，上学时间段内中小学生易发生跑跳和路上逗留等不安全行为，放学时间段内中小学生更易发生追逐和跑跳等不安全行为；一天4个时段内中小学生最容易发生的不安全行为是跑跳行为，最少发生的不安全行为是推搡行为，但是其危险性相对于跑跳行为更大，因此需要采取措施对中小学生这种不安全行为加以控制。

2.2 中小学生性别与不安全行为因果关系的卡方检验

本文采用SPSS软件，对中小学生性别与不安全行为、跑跳行为、追逐行为、推搡行为、路上逗留行为是否有因果关系进行卡方检验，即检验上述推断，其卡方检验结果见表3至表12。

(1) 检验中小学生性别与不安全行为是否有因果关系：报表解释显示，SPSS软件共读取80笔有效观察值，缺失值为2，在中小学生性别与不安全行为两个变量上有效值为97.6%(见表3)；SPSS软件所输出的百分比同质性卡方检测结果显示，χ2值为65.333，自由度为48，p值为0.049(见表4)，已达到0.05的显著水平，表明中小学生性别的不同与不安全行为的发生有显著的因果关系，男生比女生更容易出现不安全行为。

表3 中小学生性别与不安全行为观察值处理摘要

表4 中小学生性别与不安全行为卡方检测结果

注：a为98 资料格 (100.0%)预期的计数小于5,预期的计数下限为0.50。

(2) 检验中小学生性别与跑跳行为是否有因果关系：报表解释显示，SPSS软件共读取80笔有效观察值，缺失值为2，在中小学生性别与跑跳行为两个变量上有效值为97.6%(见表5)；SPSS软件所输出的百分比同质性卡方检测结果显示，χ2值为53.667，自由度为31，p值为0.007(见表6)，已达到0.05的显著水平，表明中小学生性别的不同与跑跳行为的发生有显著的因果关系，男生易出现跑跳行为，男女生比约为2∶1。

表5 中小学生性别与跑跳行为观察值处理摘要

表6 中小学生性别与跑跳行为卡方检测结果

注：a为64 资料格(100.0%)预期的计数小于5，预期的计数下限为0.50。

(3) 检验中小学生性别与追逐行为是否有因果关系：报表解释显示，SPSS软件共读取80笔有效观察值，缺失值为2，在中小学生性别与追逐行为两个变量上有效值为97.6%(见表7)；SPSS软件所输出的百分比同质性卡方检测结果显示，χ2值为47.733，自由度为18，p值为0.000(见表8)，已达到0.05的显著水平，表明中小学生性别的不同与追逐行为的发生有显著的因果关系，男生易出现追逐行为。

表7 中小学生性别与追逐行为观察值处理摘要

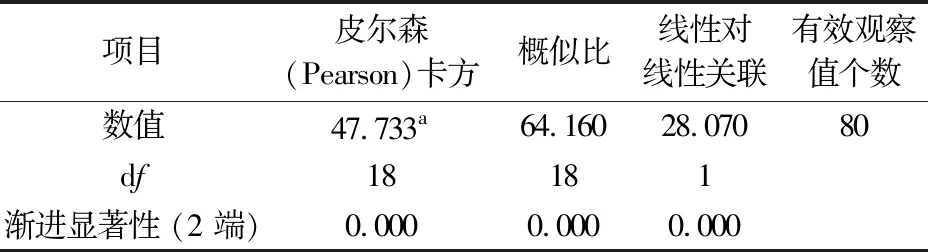
表8 中小学生性别与追逐行为卡方检测结果

注：a为36资料格(94.7%)预期的计数小于5,预期的计数下限为0.50。

(4) 检验中小学生性别与推搡行为是否有因果关系:报表解释显示，SPSS软件共读取80笔有效观察值，缺失值为2，在中小学生性别与推搡行为两个变量上有效值为97.6%(见表9)；SPSS软件所输出的百分比同质性卡方检测结果显示，χ2值为36.418，自由度为14，p值为0.001(见表10)，已达到0.05的显著水平，表明中小学生性别的不同与推搡行为的发生有显著的因果关系，男生发生推搡行为的概率较大。

表9 中小学生性别与推搡行为观察值处理摘要

表10 中小学生性别与推搡行为卡方检测结果

注：a为26资料格(86.7%)预期的计数小于5,预期的计数下限为0.50。

(5) 检验中小学生性别与路上逗留行为是否有因果关系：报表解释显示，SPSS软件共读取80笔有效观察值，缺失值为2，在中小学生性别与路上逗留行为两个变量上有效值为97.6%(见表11)；SPSS软件所输出的百分比同质性卡方检测结果显示，χ2值为41.755，自由度为24，p值为0.014(见表12)，已达到0.05的显著水平，表明中小学生性别的不同与路上逗留行为的发生有显著的因果关系，女生发生逗留行为的概率较大，男女生比约为1∶2。

表11 中小学生性别与路上逗留行为观察值处理摘要

注：a为48资料格(96.0%)预期的计数小于5，预期的计数下限为0.50。

3 结论与建议

本文通过对中小学生人群聚集处不安全行为的倾向及其影响因素进行描述统计分析和卡方检验，研究了中小学生不安全行为特征表现的相关性和差异性，得出如下结论：

(1) 监控视频统计结果显示：早中晚4个时段内，学校门口处中小学生人流高峰期是中午放学时间段，中小学生人流量相当于其他时段的2～3倍，人流量约为700人，中小学生不安全行为发生的次数在该时段内最多；其他时段内校门口处中小学生人流量基本持平，其在250～300人之间。

(2) 早中晚4个时段内学校门口处中小学生人流量不同，但是中小学生不安全行为发生的概率基本相同，约为21.35%，即每5名学生约有1名可能发生不安全行为。

(3) 监控视频统计结果显示：中小学生的主要不安全行为有跑跳、追逐、推搡和路上逗留等行为；不同时间段内中小学生出现的不安全行为有一定的差异，上学时间段内中小学生易出现跑跳和路上逗留等不安全行为，放学时间段内中小学生易发生追逐和跑跳等不安全行为；4种主要不安全行为中，跑跳行为在各时间段内发生的概率都较大，推搡行为在各时间段内发生的概率都较小。

(4) 卡方检验结果显示：中小学生中，男生比女生更容易出现不安全行为；男生易出现跑跳不安全行为，发生该不安全行为的男女生比约为2∶1；中小学生性别的不同与追逐、推搡不安全行为的发生有显著的因果关系，男生发生追逐、推搡不安全行为的概率较大；中小学生性别的不同与路上逗留不安全行为的发生有显著的因果关系，女生发生逗留不安全行为的概率较大，男女生比约为1∶2。

中小学生易发生不安全行为，是学校安全的重要影响因素，也是学校安全管理的重点。另外，学校周边环境也存在较多的危险因素，如学生骑车上学、家长开车或骑电动车送学生上放学等，易造成学校门口处人员冗杂，聚集学生家长、社会闲散人员、小摊小贩等。因此，针对中小学生的不安全行为及其学校周围环境的不安全状态，学校须加强对中小学生的安全管理，并消除学校周边环境的不安全状态，具体对策与建议如下：

(1) 消除学校周边环境的不安全状态。学校应控制学校门口的车行速度，禁止自行车、电动车等在学校门口的通行停靠；设置专门的接待室，用于家长等待学生放学，防止学校门口聚集大量人员，以避免学校门口拥堵；家长通过刷卡进出接待室，过滤掉社会闲散人员，消除其对学生的潜在威胁。

(2) 加强安全自护教育，提高学生的安全意识。为了创造一个安全的学校环境，学校管理者需要对学生进行安全教育，并将安全教育纳入教学内容，定期组织安全演练，培养学生的安全习惯，同时提高学生对生命的认识，懂得保护自己的生命和尊重他人的生命。

(3) 建立行为安全管理组，纠正学生的不安全行为。学校管理者可将行为安全管理理论应用于学生的行为管理中，成立行为安全管理组，该组成员要及时与发生不安全行为的学生沟通，讨论其正在进行的行为的危险性，并通过表扬和批评，消除学生的不安全行为，最大程度地减少学生再次发生该种不安全行为的可能性。值得注意的是，与学生的沟通要做到公开、理解、尊重，以减少学生的抵触感，保证他们在没有监督人员在场的情况下，也自愿控制自身的不安全行为。

(4) 行为安全激励机制。不管对安全的影响如何，缺少激励机制将会很大程度上妨碍学校对学生进行安全管理。为了实现安全行为的持续改进，学校采取行为安全激励机制激励学生采取安全的行为是一个非常重要的方面。