基于随机介质理论分析盾构隧道开挖引起的地表沉降

张 府， 陈有亮， 李 林

(1.上海理工大学 环境与建筑学院， 上海 200093； 2.上海隧道股份有限公司， 上海 200082)

1 研究背景

近年来，随着城市化的进程，大量的人口涌入城市，交通拥堵作为一个严峻的问题受到广泛关注。各大城市纷纷修建地铁及交通隧道来缓解交通压力，而盾构法是城市隧道开挖常用的一种方法。地铁隧道的开挖必定会扰动周围的土体，尤其是在城市中，建筑物密集，地下与地上环境复杂。为了减小对开挖隧道周围土体环境及建筑物的影响，合理控制隧道开挖引起的上部土体变形和沉降，必须对开挖引起的地表沉降进行有效地预测，进而采取积极的预防措施。

针对盾构法施工引起的地表位移，国内外常用的预测地表沉降的方法有：以Peck公式为主的经验法[1]、有限单元法[3]、理论分析法[5]、模型试验法[6]等。随机介质理论是近年来计算隧道开挖引起地表沉降常用的方法之一。20世纪50年代，波兰学者Litwiniszyn[7]通过煤层以及地表移动研究，基于沙箱模型试验，应用严密的数学方法，提出五大公理，进而建立了随机介质理论，该理论在采矿工程中得到了广泛应用，刘宝琛等[8]将此理论应用到煤矿地表移动及变形的规律。阳军生等[9]将随机介质理论扩展到城市隧道开挖引起的地表移动和变形计算，并分析了不同隧道施工方法引起地表位移的计算。施成华[10]将此理论应用到地铁隧道施工引起的地表沉降和变形研究，并对多种隧道施工工况下地层变形进行了研究，分析了任意断面收敛模式的横向地表沉降及纵向沉降预测问题。韩煊等[11]通过反分析的方法，对随机介质理论所需的两个主要参数提出了简便高效的工程确定方法。刘波等[12]将随机介质理论应用到双线平行隧道开挖引起的地表变形预测。Yang等[13]提出了适用于单线和双线隧道的随机介质理论简化理论。胡斌等[14]运用随机理论简化公式，基于地表沉降数据，通过反分析得到断面收敛面积与主要影响角，并分析了两个计算参数与上覆岩土黏聚力和内摩擦角的关系，提出了相应的确定方法。魏纲等[15]针对双线水平隧道建立了修正的随机介质理论方法， 并考虑了先行隧道和后行隧道参数取值不同的情况。傅鹤林等[16]在极坐标系中推导了在偏压地形中，浅埋隧道开挖引起的地表沉降。

2 随机介质理论及简化

随机介质理论假设地层沉降是由于隧道收敛变形而引起的，将整个隧道断面的开挖等效成无限多个开挖单位的开挖，通过积分方法计算开挖单元对上部地层影响的总和，进而得到地层位移。对于地层采用整体坐标系(x,y,z)，对于隧道开挖部分采取局部坐标系(ξ,ζ,η)，如图1所示。

图1 单元开挖示意图

由于单元dξdζdη开挖引起的距离开挖单元(x,y)的地表某一点的沉降We(x,y)表达式为：

(1)

式中:r(z)为单元开挖在z水平上的主要影响范围；x为地面任一点到开挖单元的水平距离；y为地面任一点到开挖单元的垂直距离。

对于单元开挖沿隧道方向无限长时，可将其按平面应变问题进行考虑。则单元开挖引起的地表沉降为：

(2)

式中:β为上部岩层主要影响角。

根据Knoth提出的经验公式tanβ=z/r(z)，其含义如图2所示。

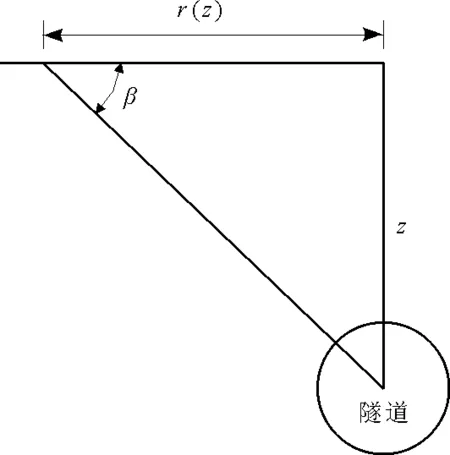
图2 主要影响角和影响半径

假定整个隧道断面开挖区Ω内的每一个单元开挖后完全塌落，则根据叠加原理得到此时的地表沉降为:

(3)

隧道开挖初始断面为Ω，隧道建成后的开挖断面由Ω收敛为ω，如图3所示。

图3 隧道开挖示意图

根据叠加原理可知，地表最终沉降为开挖范围Ω引起的沉降与开挖范围ω引起的沉降之差：

W(x)=WΩ(x)-Wω(x)

(4)

(5)

式中:积分的上下限a、b、c、d为隧道断面收敛前的积分界限；e、f、g、h为隧道断面收敛后的积分界限。

在随机介质理论研究中，大多假定隧道开挖产生的收敛模式为均匀收敛，即隧道开挖后四周向开挖中心产生均为ΔR的变形。然而，实际工程中隧道的收敛模式受多种因素的影响，如土层分布、注浆压力、施工方法等，隧道开挖后实际的收敛模式并不是均匀的。因此，有的学者假定隧道开挖后产生的收敛为不均匀收敛。由于地层损失而发生均匀收缩，在重力的作用下产生下沉，收敛后的隧道断面与初始断面为两圆相切的现象，即隧道顶部下沉高度为2ΔR，隧道底部的隆起为0，此类收敛模式又称为单间隙模式。

除单间隙模式以外，还有双间隙模式以及综合考虑隧道收敛和下沉的不均匀收敛模式。

根据隧道产生均匀收敛和不均匀收敛模式的不同，隧道开挖前后的积分界限如表1所示。

表1 均匀与不均匀收敛积分界限

根据Yang等[13]提出的随机介质理论简化理论，可得到简化公式为：

W(x)=WΩ(x)-Wω(x)

(6)

式中:R为隧道开挖半径;r为收敛后隧道半径;z为隧道埋深;ΔA为隧道断面收敛面积。

根据韩煊等[17]对不同收敛模式和不同埋深的隧道开挖产生地表变形进行分析的结果，隧道开挖断面不均匀收敛计算的地表沉降大于均匀收敛模式，且二者的计算结果差异随着隧道埋深的增加逐渐减小，即埋深越大，隧道断面的收敛模式对地表沉降的影响越小。在隧道的相对埋深为5时，二者计算差异略小于10%，且两种收敛模式计算的最大误差不超过20%。因此公式(6)的简化是可行的。

在隧道开挖导致的地表变形实测数据的基础上，通过反分析得到随机介质理论法的两个关键参数，即隧道收敛面积ΔA和主要影响角的正切值tanβ。通过分析这两个参数与实际工程易测得的数据(如埋深和土体力学参数等)的关系，提出简单有效的工程确定方法，可以大大提高随机介质理论法的应用。

3 本文研究方法

本文在隧道开挖导致的地表变形实测数据的基础上，利用Matlab程序，根据lsqcurvefit函数进行最小二乘拟合，反分析计算得到随机介质理论简化公式的两个主要参数，主要影响角的正切值tanβ以及隧道断面收敛面积ΔA，进而分析这两个主要参数与其他工程数据的关系，找到简单有效的工程确定方法。

从主要影响角的定义可以得知，主要影响角β控制地表沉降槽i的宽度。长期以来，国内外许多学者对沉降槽宽度i的规律进行了研究，并提出了各种有效的计算公式。韩煊等[17]通过对国内外的相关研究成果进行归纳总结，将关于地表沉降槽宽度的公式分成了以下4类：

(1)第1类公式：i与隧道的绝对埋深有关，与此同时在公式中加入土的强度参数；

(2)第2类公式：i与隧道的相对埋深成幂函数的关系；

(3)第3类公式：i是关于隧道半径和隧道绝对埋深的线性函数；

(4)第4类公式：i仅是关于隧道绝对埋深的线性函数。

通过对照上述公式及发表的年代，只有Loganathan[18]采用的是第2类公式，其它基本都随着时代的变化，i的计算公式从第1类演变为第2、第3、第4类公式，且处于不断简化的趋势。

因此，在基于隧道开挖导致地表变形的实测数据经反分析得到的主要参数ΔA和tanβ的结果上，对两个参数与隧道埋深或相对埋深之间的关系进行分析。

4 工程实例

本文以虹梅南路隧道先行开挖西线工程的地表沉降实测数据为例进行分析。隧道全长5 260 m，采用盾构法隧道和明挖顺做法进行主要结构的施工，其中盾构法施工的隧道长3 390 m。隧道盾构段采用直径为14.93 m的泥水平衡盾构机进行施工，下埋隧道外径为14.5 m。隧道中心埋深18～52.2 m。西线工程共有45个监测断面，每个监测断面有5个监测点来监测地表沉降，距离隧道轴线的距离分别为0、2.5、7.5、12.5 m。

考虑到监测数据的完整性以及地质条件的影响，本文选取了20个断面进行研究。通过对实测数据进行拟合分析，实测数据反分析结果如表2所示，典型断面(W1680和W1345断面)的拟合结果如图4和5所示。

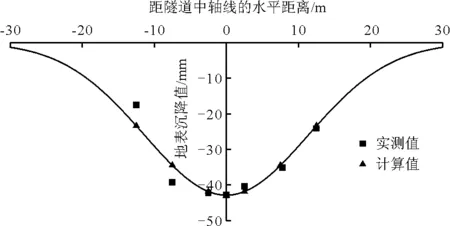
图4 W1680断面的地表沉降拟合

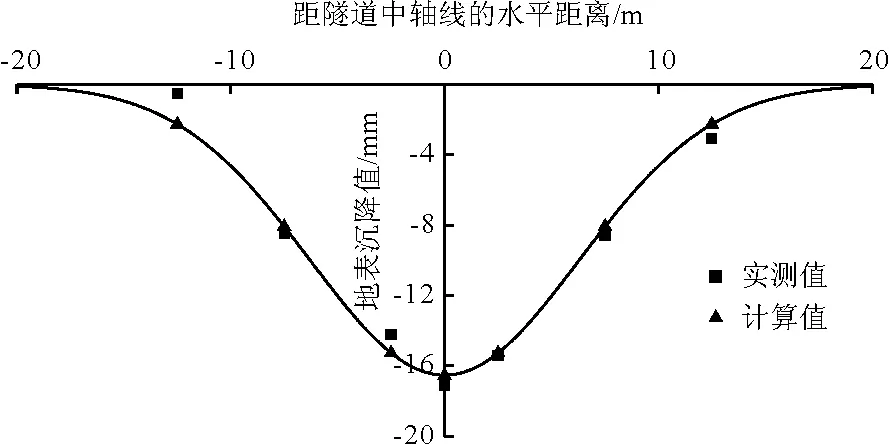
图5 W1345断面的地表沉降拟合

由图4和5可以看出，通过随机介质理论计算出的地表沉降值与典型断面的实测沉降值拟合效果较为理想。

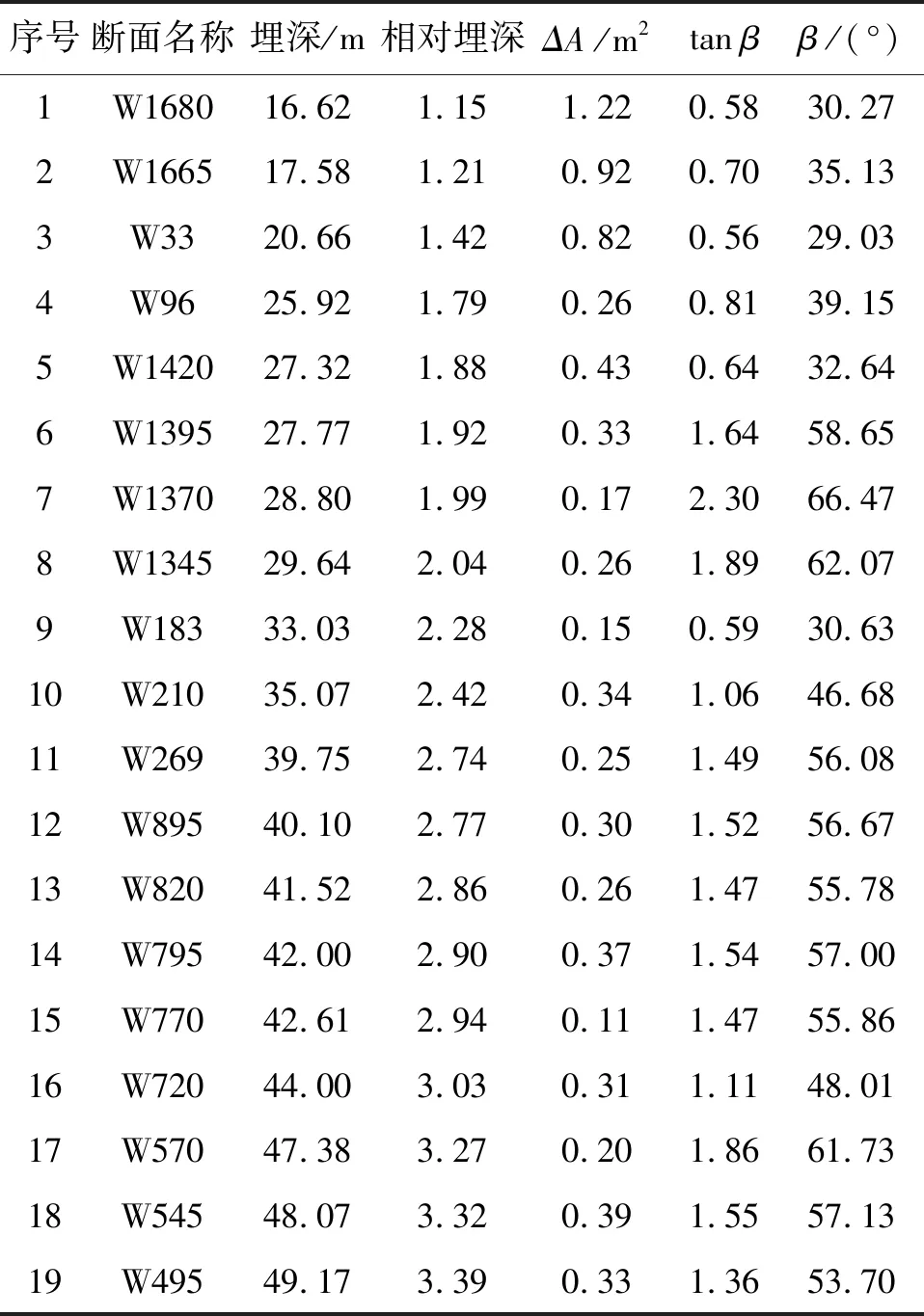
表2 实测数据反分析结果

5 计算参数与埋深之间的关系

将表2的结果进行整理，可以得到隧道断面收敛面积ΔA与隧道埋深的关系，如图6所示。

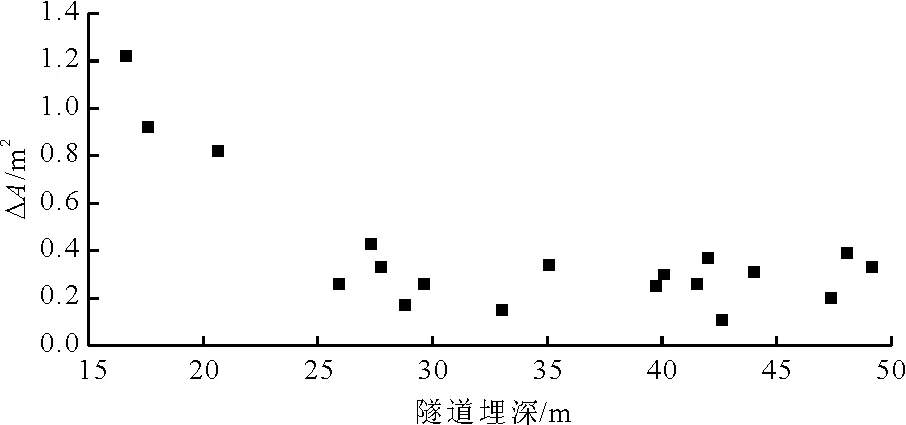
图6 ΔA与隧道埋深的关系

从图6中可以看出,当隧道埋深在20 m以上时，即相对埋深小于1.5时，隧道断面收敛面积ΔA较大，产生的地表沉降也会相应地增加。随着隧道埋深的增加，ΔA也在减小，绝大多数处于0.2～0.4 m2之间，即埋深或相对埋深越大，产生的地层损失越小，隧道开挖导致的地表沉降也较小。

将主要影响角的正切值tanβ与隧道埋深的关系进行整理，结果如图7所示。

图7 tanβ与隧道埋深的关系

由图7可以看出，在隧道埋深小于30 m时，即相对埋深小于2时，tanβ数值较小，随着隧道埋深的增加，tanβ的整体趋势是增加的，tanβ与埋深大致满足tanβ=0.035z-0.098的关系。

6 结 论

(1) 本文基于随机介质理论简化公式，针对虹梅南路隧道开挖引起的地表沉降，经过反分析计算得到了随机介质理论简化公式中的两个关键计算参数ΔA和tanβ，并对这两个关键参数与隧道埋深或相对埋深之间的关系进行了研究。

(2) 通过对虹梅南路隧道进行分析，结果表明：本文的计算值与实测值拟合良好。对于浅埋隧道，ΔA的取值较大且较离散；随着隧道埋深的增加，当隧道埋深大于20 m时，ΔA的取值较稳定，且大部分处于0.2～0.4 m2之间。tanβ随着埋深或相对埋深的增加，整体呈现出增加的趋势，且tanβ与埋深大致满足tanβ=0.035z-0.098的关系。