某水库溢洪道方形消力竖井优化研究

石胜友， 高华峰， 李 琳

(1.新疆农业大学 水利与土木工程学院， 新疆 乌鲁木齐 830052; 2.新疆伊犁州水利电力勘测设计研究院， 新疆 伊宁 835800)

1 研究背景

竖井消能具有结构简单、经济合理、消能效率高的优点，在水利水电工程、市政排水工程中有较广泛的应用。射流入井后并不直接冲击井底或井壁，而是在井内形成光滑的反弧曲线，一般近似由一个或两个反弧半径组成。井内有顺时针方向的剧烈旋滚，井棱角处有掺气的立轴漩涡消除部分水流能量。消力井的尺寸对井流流态有显著的影响，因此，国内研究人员针对消力井深、井宽等水力计算和泄流特性开展了一些研究。郭雷等[1]结合金平水电站对具有消能井的溢洪道压力特性及消能率等问题进行了研究。陈永铭[2]结合南平市区排洪隧洞工程，对竖井式溢洪道中消能井的水流流态、水面线和流速分布进行了研究。廖常德等[3]通过对6个新型竖井消能溢洪道的水力模型试验成果对比分析，认为采用竖井消能的溢洪道具有消能率高和造价低的特点。赵灿华[4]针对旋流式竖井通过模型试验对竖井的压强、空腔形状以及消能特性等进行了研究。符晓等[5]通过绩溪抽水蓄能电站下水库竖井式溢洪道水工模型试验表明:溢洪道泄流能力能够满足要求；溢洪道采用"竖井十台阶面泄槽+消力池"的联合消能形式，消能率较高。陈小威等[6]基于不同消能井深下的压强试验表明：压强随井深的变化而变化。张宗孝等[7]对不同直径消力井下的压强特性进行了研究。周斌斌等[8]使用FLUENT软件对溢洪道进行数值模拟实验与物模试验进行分析，发现数模与物模试验吻合良好，为溢洪道结构优化提供技术保障。王海军等[9]采用Fluent软件中RNGk-ε和VOF模型对某溢洪道进行了数值仿真模拟研究，数值模拟结果与原型观测数据基本一致，验证了所采取数值仿真模拟方法的合理性。《水力计算手册(第二版)》[10]也给出了消力井设计的经验公式。由于井流是典型的三维高速流动，而用于初步设计的经验公式往往是按照一维射流运动，忽略摩擦阻力，沿竖井深度上各点的压强按静水压强分布考虑获得的，在这些假设基础上，从理论上尚无法正确预测竖井内的流态、水深和压强分布，竖井的设计仍然需要通过水工模型试验对其设计方案进行验证，为设计提供参考。

某水库主要由拦河大坝、溢洪道等建筑物组成，属Ⅳ等小(1)型工程。水库正常蓄水位2 083.00 m，设计洪水位2 084.11 m，校核洪水位2 084.89 m。溢洪道布置在大坝左岸，采用侧槽溢洪道，由控制段、调整段、竖井段、无压泄槽段和消能段组成。溢洪道布置轴线水平投影长度288.75 m，其中溢流堰控制段长40.88 m，调整段20 m，竖井段(顺水流方向的长度为5 m，宽为6 m，高度为39.45 m，井深为5 m)，泄槽段长180 m，出口消能段58.75 m。本研究针对原设计方案溢洪道的方形消力竖井开展水工模型试验，获得不同工况下竖井泄洪流态、竖井上、下游壁面时均压强特性和空化数的分布规律。同时，应用RNGk-ε模型和VOF方法对消力竖井内泄流流态进行数值模拟，优化竖井结构尺寸，为工程设计提供参考。

2 模型设计与试验方案

2.1 模型设计

模型采用正态模型，按重力相似准则设计。根据试验室条件，物理模型比尺如表1所示。模型模拟总长约为330 m，其中库区段40 m，下游段288.75 m。溢洪道控制段、调整段、竖井段、无压泄槽段、消能段均采用有机玻璃板制作，其糙率为0.008～0.009，根据比尺换算成原型为0.014～0.016，满足相似要求[11-13]。海漫下游抛石坑内放入钢筋笼，钢筋笼原型尺寸为1 m×1 m×2 m(宽×高×长)，模型尺寸为4 cm×4 cm×8 cm(宽×高×长)，模型钢筋笼内抛石直径为1～3 cm。溢洪道原设计方案结构布置如图1所示。

表1 模型比尺

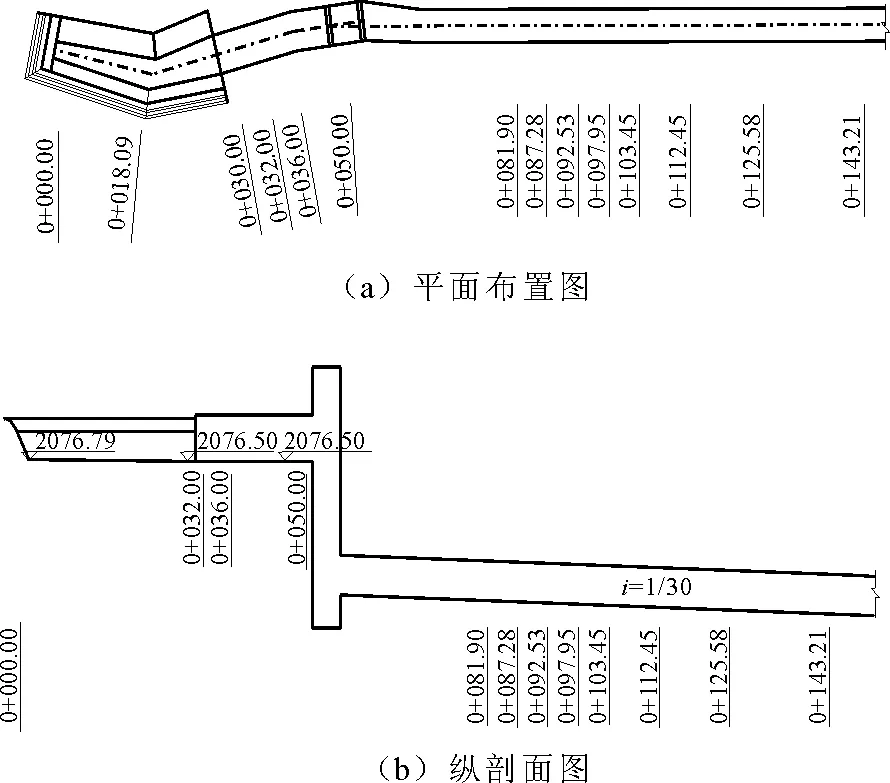
图1 溢洪道原设计方案布置图(单位：m)

2.2 模型试验方案

对溢洪道进行20年一遇洪水、设计洪水、校核洪水流量下的模型试验，具体试验工况见表2。试验中观察溢洪道消力竖井和泄槽段的流态并拍照记录。在溢洪道上共布置了24个典型断面进行水深量测。在每一个典型断面上布置左、中、右3条垂向测线，沿相对水深的1/3处布置测点量测流速。在消力竖井上、下游壁面的垂向对称轴和底板中线上共布置了18个测点量测压强，如图2所示。为了计算消力井的消能率，以图1(b)中0+050.00 m断面作为消能竖井入口断面，以0+093.50 m断面作为出口断面量测其相应的水位和流速。

模型由水库供水，通过控制水库水位来控制流量。模型流量量测系统分别由上游量水堰和下游量水堰组成。溢洪道流速用毕托管测量，压强用测压管测量，溢洪道各典型断面水深用钢板尺测量。

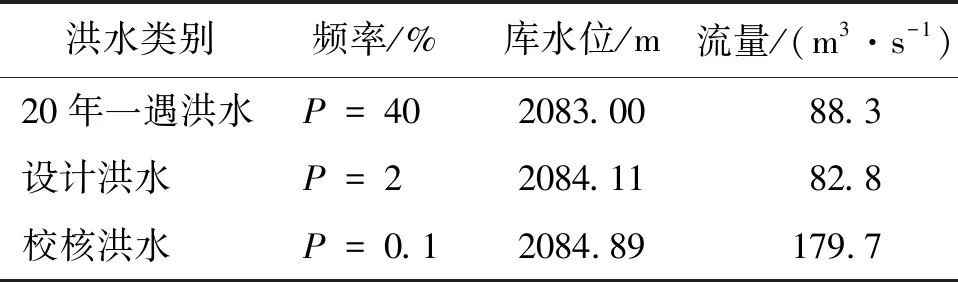
表2 模型试验工况

3 消力竖井方案优化

3.1 原设计方案试验

溢洪道泄设计洪水和校核洪水时消能竖井内的泄洪流态如图 3 所示。水流以一定的初速度作平抛运动射入方形消能井中，受下游井壁面约束，射流直接冲击下游井壁，溅起水花并从井壁反射回流，回流水面高程低于调整段出口水面高程。校核洪水时，射流冲击壁面出现典型面流，面流几乎与调整段末端水面高程齐平，射流冲击壁面溅起的水花顶高程为2 083.00 m(设计洪水为2 079.50 m)；碰壁反射水流的长度明显增加，但不影响泄洪。从图3(c)可以看出，校核洪水时水流呈乳白色，含气量大于设计洪水工况，竖井内空腔沿垂向的高度为5 m，沿水流流向的宽度为2 m，明显小于设计洪水工况(空腔高度为9 m，宽度为3 m)。在溢洪道宣泄20年一遇洪水时，水流流态大致和设计洪水相似，只是空腔的体积略大于设计洪水时的空腔体积。

不同泄洪工况下的消能率计算结果见表3。从表3可以看出，校核洪水时竖井消能率为50.95%，低于设计洪水流量。水流射入消能井后，水从井底和井壁反射，沿井壁向上回升与下落的水流相互碰撞，水流旋滚上升与射流撞击形成强掺混、强紊动、强掺气的水流，消耗部分能量。校核洪水下由于消能井的井深较浅，射流撞击下游井壁后未经消能就直接进入泄洪隧洞，消能不充分。同时，由于调整段断面宽度和消能方井的宽度相同，泄洪时竖井内水流掺气不充分，使消能率降低。

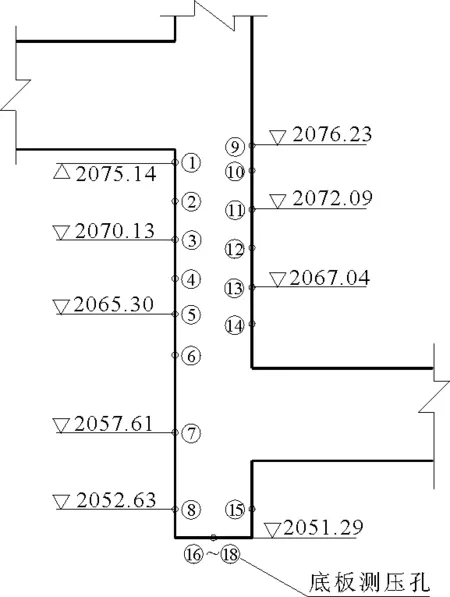
图2 溢洪道模型消能井内测压孔布置图

根据实测数据按规范推荐的公式(1)、(2)估算了水流空化数。具体结果见图4。

(1)

(2)

式中：σ为水流空化数；h0为计算断面处的动水压力水头，m；ha为计算断面处的大气压力水头,m；hv为水的汽化压力水头,m；v0为计算断面处的断面平均流速,m/s；为计算断面处高程，m。按水库溢流侧堰堰顶高2 083.00 m计算得h0=8.02 m，hv与水的温度有关，假定泄流时平均水温为20℃，则hv=0.24 m[14]。

图4为不同泄洪工况溢洪道竖井各典型测点压强水头及空化数。由图4可知，在各级洪水工况下，由于水舌脱壁且补气不充分，竖井上游壁面自高程2075.14～2067.61 m约7.5 m(1～5号测点)的范围内均有负压，最小负压在2号测孔附近，对应空化数为0.32；高程2067.61～2052.63 m约15m(5～8号测点)的范围是正压，最小空化数为0.75。水舌沿下游井壁面射入水垫，射流流速愈向下愈大，壁面压强随之减小，在竖井下游壁面高程2076.23～2072.09 m约4 m(9～12号测点)范围为正压；2069.59～2064.66 m约3 m范围(13～15号测点)内均为负压，最小负压水头为-7.12 m(校核工况)，对应空化数为0.13。自高程2064.66 m至竖井底板，受水垫消能的影响，流速减小，压强由-1.07 m增大到12.52 m。由于上游井壁面受顺时

针漩滚回流影响，壁面流速小于下游壁面，因此上游壁面1～5号测点真空值小于下游壁面13～15号测点。溢洪道宣泄设计洪水和校核洪水时，方井内局部壁面的空化数小于初生空蚀数，壁面可能产生空蚀破坏，影响建筑物的安全运行。

泄流流量越大，则消力竖井内的水位越高，设计洪水时的底板最大压强为122.4 kPa；校核洪水时消力井的底板最大压强为176.7 kPa。

图3 溢洪道原设计方案不同泄流量水流态图

工况竖井入口断面h1/m(v22/2g)/mE1断面0+093.5 mh2/m(v22/2g)/mE1((E2-E1)/E1)/%20年一遇24.131.6625.793.007.9110.9157.70设计洪水24.262.3726.633.008.2711.2757.68校核洪水25.004.3629.364.759.6514.4050.95

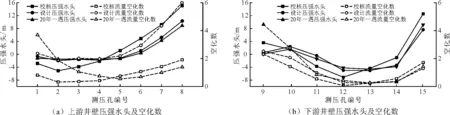
图4 不同泄洪工况溢洪道竖井各典型测点压强水头及空化数

3.2 修改方案数值模拟

为了改善消力井壁面压强分布，同时进一步提高消力井的消能率，在保持溢洪道其他尺寸不变的条件下，对消力竖井顺水流方向长度、宽度和消力井深度进行了不同调整，具体修改方案见表4。应用紊流精细数值模拟的方法对修改方案在校核洪水工况下开展了数值模拟试验，并对模拟数据进行分析，选出最优方案。

3.2.1 数模计算区域、控制方程及边界条件 由于竖井内的流态主要取决于上游侧槽内的水位和泄流流量的大小，因此以桩号0+020.00 m断面为起始断面建立模型对竖井内的流态影响较小。竖井下游泄洪洞段为急流，急流到急流不会影响上游竖井内的泄洪流态。因此，以桩号0+143.21 m断面为末端出口，其下游泄流对竖井内的流态不会产生影响。同时，由于本研究主要针对消力井进行方案优化，因此以桩号0+020.00 m断面为起始断面，以桩号0+143.21 m断面为末端出口断面建立三维模型，模型包括调整段、渐变段、方形竖井和部分下游泄槽段。应用Ansys Fluent 17.0对消力井泄洪特性开展数值模拟研究，并对消力井方案进行优化。

采用RNGk-ε[15-19]模型进行数值模拟，基本方程为:

连续方程：

(3)

动量方程：

(4)

k方程：

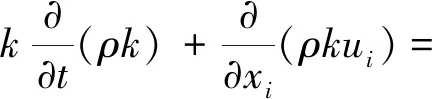
Gb-ρε-YM+Sk

(5)

ε方程：

(6)

式中：Gk为由于平均速度梯度引起的湍动能k的产生项，可由公式(7)确定；Gb为由浮力产生的湍流动能k的产生项，对于不可压流体，Gb=0。

(7)

VOF方法追踪的是网格中流体体积，具有容易实现、计算量小和精度高等优点。因此本文采用VOF法追踪气液交界面。当αw=0，模拟模型内没有水，被气充满；当αw=1时，表示溢洪道内被水充满；当0≤αw≤1时，表明管内被水和气充满。αw的控制方程为：

(8)

αw+αa=1

(9)

控制方程中的对流项和扩散项采用二阶迎风格式离散,离散后的线性代数方程组采用PISO方法进行迭代求解。

溢洪道模型进口采用速度进口边界条件，根据模型试验测得的流量和边界大小，计算出液相初始速度为4.56 m/s；出口边界为压力出口边界，相对压强为0；模拟区域底板及边墙为固壁边界，规定为无滑移边界条件，采用壁函数来修正壁面附近的低雷诺数流动区域。

表4 竖井修改方案

3.2.2 数学模型验证 由于网格数量对数值模拟结果影响很大，为得到较为准确的模拟结果，必须消除因网格数量对计算结果的影响。对原设计方案的侧槽溢洪道方形消力竖井采用8种不同数量的网格划分方案(具体见表5)进行数值模拟。图5为不同网格剖分方案下原设计方案溢洪道在宣泄校核洪水时竖井上、下游泄槽内典型断面1(桩号0+050.00 m)和断面2(桩号0+092.53 m)的水位模拟值。由图5可知，当网格数量达到80×104后，典型断面水位值随网格数量的继续增加而基本保持不变，网格数量对模拟结果影响可以忽略。因此，考虑计算精度和时间，选择方案7进行计算。

表6为网格剖分方案7下溢洪道在宣泄校核洪水时竖井上、下游泄槽内水位数值模拟结果与模型实验结果对比。从表6可以看出，该方案下的水位模拟值与实测值吻合较好，最大误差为5.9×10-4，表明本文所建立的数学模型及其经验参数正确。

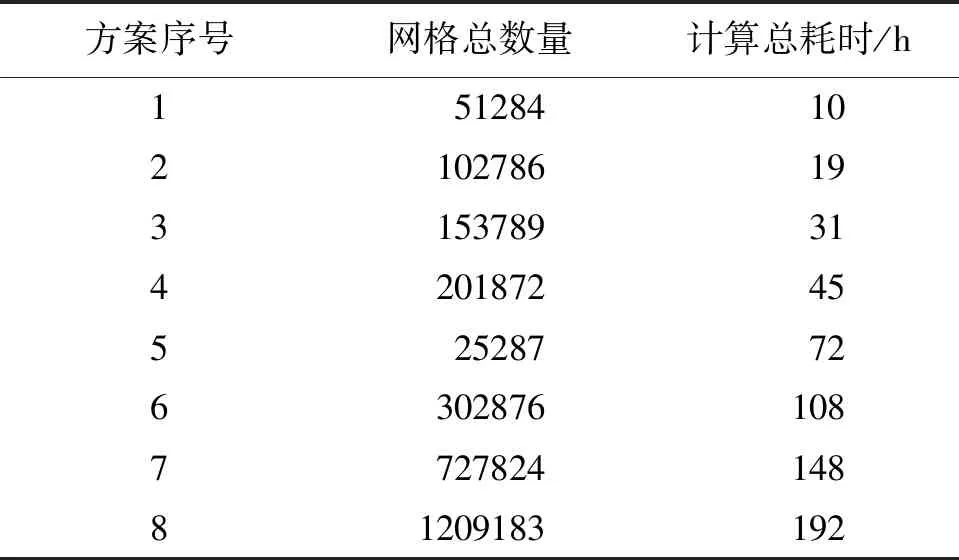
表5 不同网格划分方案及对应的计算时间

表6 校核流量下水位数值模拟结果与模型试验实测结果对比 m

3.2.3 修改方案消能方井流态图 通过建立三维数学模型，对不同修改方案的消力井在校核洪水工况下进行数值模拟。图6为不同修改方案校核洪水时消能竖井内流态图。由图6可得，方案1、2、4消能竖井内流态和原设计方案相似(见图3(c))。数模结果表明，方案1、2、4井内射流冲击壁面形成的面流水面高程分别为2080.70、2080.10、2079.20 m；回流长度分别为3.70、3.20、2.80 m。井内水垫的水面高程约为2064.99、2060.79、2064.91 m。从以上结果可看出，竖井的深度增加，则面流水面高程降低，回流长度减小；竖井的长度增加，则水流撞击下游井壁点略微降低，但是对壁面流速及掺气没有影响。方案1、2、4竖井内空腔沿垂向的高度分别为7 、11 、7.1 m，沿水流流向的宽度分别为2.7 、2.3 、2.9 m，明显大于原方案(空腔高度为5 m，宽度为2 m)。这是因为井内壅水量一定，增大井深导致井内水位降低，空腔体积增大。由图6(c)可以看出，方案3中保持井深8 m不变，井宽度由5 m加宽至8 m后，竖井内空腔形状明显不同于其他方案，射流冲击壁面溅起的水花顶高程为2082.70 m、反射水流长度为4.3 m，较原方案大。由于加大了井宽，水流并不受井壁摩擦力作用，水流撞击下游井壁速度加大，溅起的水花顶高程增大，回流增大，竖井内的水位约为2064.99 m。由于竖井宽度的增大，使射流不受两侧井壁约束撞击壁面后部分水流往两侧扩散，薄层水流沿井壁下泄，其空腔形状是倒三角形，内部形状和其余方案相同，为弧形空腔。

图5 不同网格数方案与竖井上、下游典型断面模拟水位关系曲线

3.2.4 修改方案下方井壁面时均压强和空化数 表7为原校核洪水方案和修改方案相同测点的压强和空化数对比。从表7可知，各个修改方案中消力井上游壁面1～4号测压点、下游壁面12～14号测压点范围内均有负压，与原方案负压区域基本一致，且方案1、2、4中1～4号测点、12～14号测点压强和空化数与原设计方案相比几乎没有变化，这是因为增加井深和顺水流方向长度，只影响井内水位，不影响射流流速，壁面压强及空化数基本保持不变，所以增大井深和顺水流方向的长度不能改变负压的大小。但是在方案3中，竖井上游壁面1～4号测点压强与原设计方案相比分别提高了37.04%、35.51%、44.02%、49.55%，最小空化数由0.32提高至0.50；井下游壁面12～14号测点压强与原设计方案相比分别提高了43.71%、36.64%、68.89%，最小空化数由0.13提高至0.38，较初生空化数大，不会发生空蚀破坏，这是因为竖井宽度加宽后，空气从水舌左右两侧补入，增加了水体内的含气量。各个修改方案中上游壁面5～8号测点在水垫范围内，各测点均为正压，其中5号测点压强最小为13.27 kPa，空化数为0.77；下游壁面9～11号测点范围也为正压，10号测点压强最小为14.74 kPa，空化数为1.90，因为此时水流流速小。与原方案相比，方案1至方案4的竖井深度增加了3～5m，因此竖井底部的压强随水垫厚的增加而增大，其中方案2的压强最大为212.45 kPa。

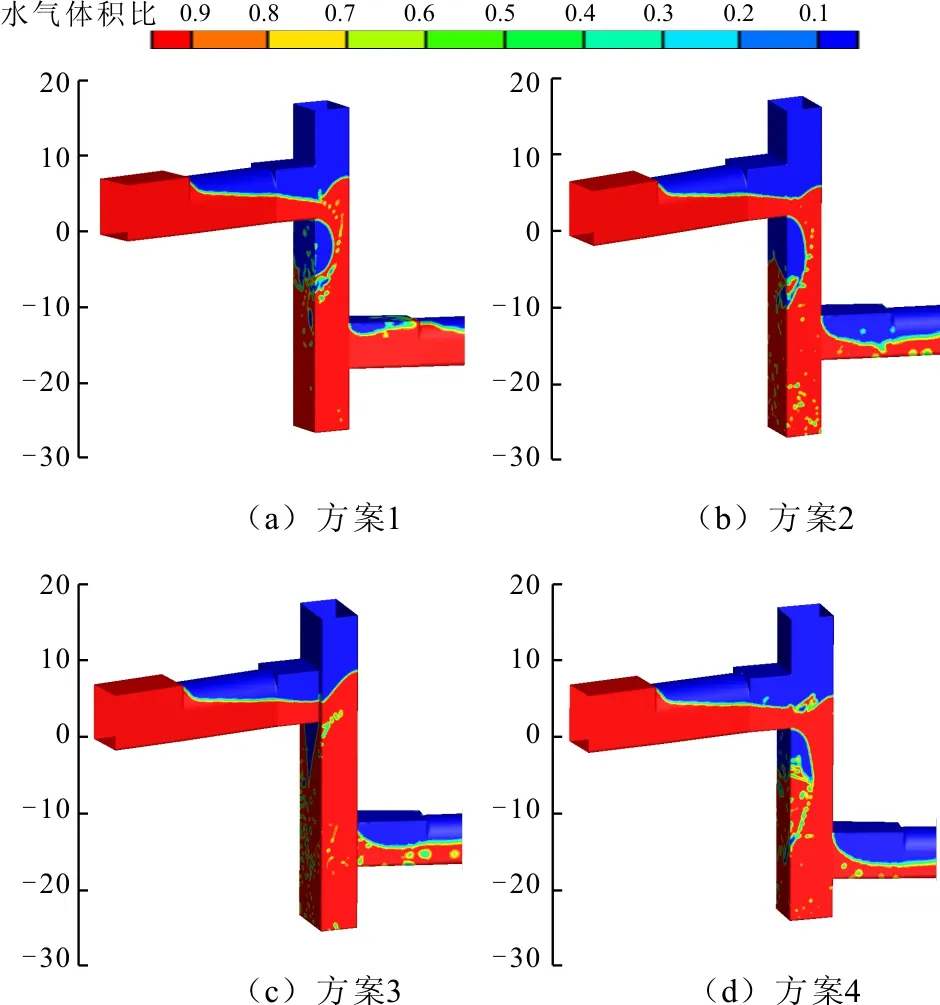
图6 校核流量下不同修改方案竖井内流态图

3.2.5 修改方案下消能方井的消能率 校核洪水位时不同方案下消能率计算结果见表8。由表8可知，相比原设计方案，方案1、2、3、4的消能率均明显得到提高，这是因为修改方案中井深增加了3～5 m，使得水垫厚度增加，射流射入水垫后形成更为充分的强掺混、强紊动、强掺气的水流以消耗更多能量。但也可以看出，方案2中虽然井深由原设计方案的5 m增加至10 m，消能率与其他方案相比，却没有明显增加，表明消力井井深增加对消能率的影响有限，井深增加到一定程度后，消能率保持不变。方案3的消能率略高于其他方案，是因为在井深相同时井宽度增加，气体从射流水舌两侧掺入，使水体含气量增加，消能率增大。方案4中增加了井的顺水流方向的长度，但与其他方案相比，消能率基本相同，表明增加顺水流方向的竖井长度对提高消能率影响很小。

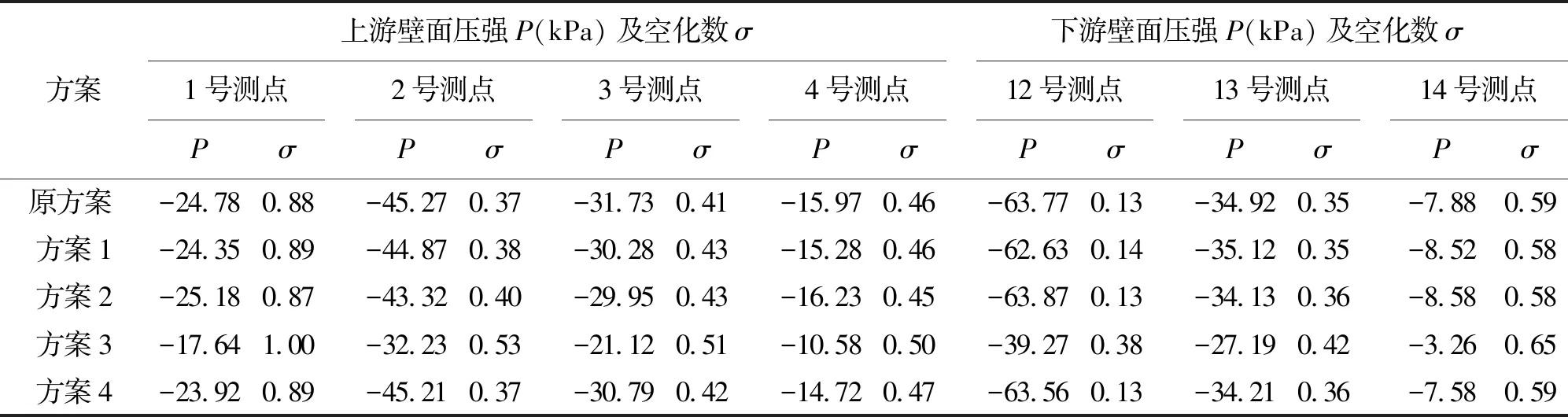
表7 不同方案竖井壁面部分测点压强及空化数对比

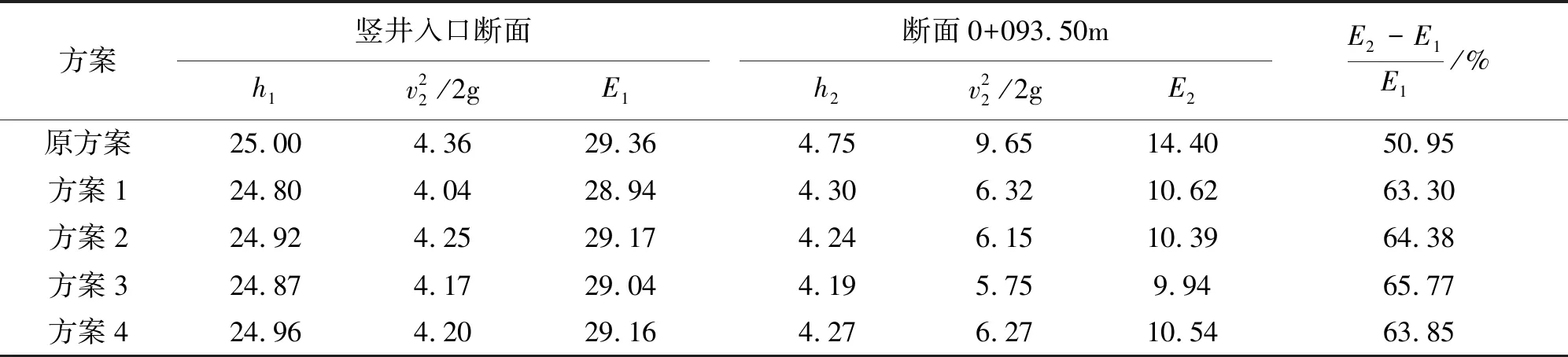
表8 不同方案校核洪水消能率

4 结 论

通过模型试验和数值模拟相结合的方法对方形消力井在典型洪水流量下的泄流特性进行研究，根据结果对消力井结构尺寸进行优化，主要得出以下结论：

(1)原设计模型试验结果表明，竖井尺寸基本不影响溢洪道宣泄设计洪水和校核洪水，竖井内面流顶高程为2 079.50 m，消能率约为57.68%和50.95%，但溢洪道宣泄设计洪水和校核洪水时竖井内局部壁面的负压较小大，最小空化数(0.13)小于初生空化数，壁面可能产生空蚀破坏，影响建筑物的安全运行。

(2)基于RNGk-ε模型和VOF方法对消力井修改方案进行了数值模拟，结果表明竖井宽度、深度和顺水流方向长度增加对竖井中空腔位置及最大负压区范围没有影响。竖井宽度增加可以有效减小壁面负压，使其空化数显著增大，改善了原设计方案中局部壁面空化数小于初生空化数的现象。竖井深度增加可提高消能率，但是井深度的增加对消能率的影响有限。顺水流方向长度增加使井内形成的面流顶高程有所降低，但其变化对消能率和壁面压强没有影响。

(3)基于文章的研究结果得到方形消能竖井的最优尺寸为：井长×井宽×井深为5 m×8 m×8 m，该方案下，竖井壁面的最小空化数为0.38，消能率为65.77%，射流撞击竖井溅起水花高程为2 082.70 m。