基于混合核SHTS-SVM的年径流预测

周有荣， 崔东文

(1.临沧润汀水资源科技服务有限公司， 云南 临沧 677000； 2.云南省文山州水务局， 云南 文山 663000)

1 研究背景

提高径流预测精度一直是水文预测预报中的热点和难点。由于河川径流预测的复杂性和不确定性，传统数理统计等方法难以获得理想的预测效果[1]。BP[2-3]、Elman[4]、RBF[5-6]、GRNN[7]等神经网络因其较好的自学习能力和函数逼近能力，在水文预测预报中得到广泛应用。但BP等神经网络基于大样本、经验风险最小以及易陷入局部极值等不足限制了它在水文中的应用[8]。研究表明，径流的形成和变化过程异常复杂，仅依靠单一的常规或非常规方法进行径流预测，往往难以达到理想的预测效果和精度，选择合理的模型与方法，建立有效的预测模型是提高水文预测预报精度的关键。

支持向量机(Support Vector Machines,SVM)基于结构风险最小化原则，能有效避免维数灾、过拟合等问题，具有高容错性、智能化和自学习等优点，已成功应用于水文预测预报[9-11]。但在实际应用中，SVM存在两方面的困难和不足：(1)SVM核函数等关键因子选取困难。常规试错法、经验法等选取SVM核函数等参数的方法已不能满足SVM应用需求。目前，除遗传算法[12](GA)等传统智能算法用于优化SVM参数外，人工鱼群算法[13](AFSA)、果蝇优化算法[14](FOA)、布谷鸟搜寻(CS)算法[15]、灰狼优化(GWO)算法[10]、文化算法[10](CA)、SCE-UA算法[10]、花授粉算法[10](FPA)、混合蛙跳算法[16](SFLA)、入侵杂草优化(IWO)算法[16]、帝国竞争算法[16](ICA)、生物地理学优化(BBO)算法[16]等群体智能优化算法被尝试用于SVM关键参数的选取，并获得一定的应用效果，但存在智能算法仿真对比验证的不足。(2)单一核函数制约SVM性能问题。核函数的选取是提高SVM预测精度的关键，每种核函数都有其优势和不足。高斯核函数属典型的局部性核函数，其局部学习能力强，但泛化能力弱；多项式核函数属典型的全局性核函数，其泛化能力强，但局部学习能力弱[17]。目前，SVM在水文预测预报中普遍采用高斯核函数，通过构建混合核函数，SVM的预测精度尚有进一步提升的空间[18]。鉴于核函数的选取和核函数参数优化对于改善SVM性能的关键性作用，为进一步提高年径流预测精度，本文利用一种新型智能算法——同热传递搜索(Simultaneous Heat Transfer Search,SHTS)算法优化混合核SVM关键参数和混合权重系数，提出混合核SHTS-SVM年径流预测模型。通过6个不同维度的标准测试函数对SHTS算法进行仿真验证，再与当前寻优效果较好的教学优化(TLBO)算法、GWO算法进行对比验证，并通过两个年径流预测算例对混合核SHTS-SVM模型进行实例验证，并与多项式核SHTS-SVM、高斯核SHTS-SVM及SHTS-BP模型预测结果进行对比，旨在验证混合核SHTS-SVM模型用于年径流预测的可行性和有效性。

2 同热传递搜索算法及仿真验证

2.1 同热传递搜索算法

热量传递搜索(Heat Transfer Search,HTS)算法是Patel等[19]于2015年提出的种群迭代随机搜索算法，该算法灵感来源于热量传递原理，通过传导、对流和辐射3种热量传递方式与周围环境系统相互作用来实现热平衡，其每次迭代包括传导、对流、辐射3个阶段之一，即在0和1之间生成一个随机数R，如果R小于1/3，则算法执行传导算子；如果R大于1/3且小于2/3，则执行对流算子；如果R大于2/3，则执行辐射算子，HTS算法通过不断迭代直至获得问题最优解，算法描述参见文献[19]。

SHTS算法是一种基于HTS改进的变体算法，该算法具有较低的计算复杂度和全局极值寻优能力，在解决高维、复杂优化问题时具有竞争性。在SHTS中，每次迭代中将种群随机分成3组，每个组分别为热量传递搜索算法的3个传热阶段之一，所有进行任何传热模式的个体都将产生一个潜在的新个体，该新个体通过适应度值评判选择接受或丢弃，且在每次迭代过程中传导、对流和辐射是并行执行的，从而大大减少了计算时间[20-21]。

参考文献[20-21]，SHTS算法简述如下：

(1)种群划分。随机将种群N分成3组，并将其分配到传导、对流和辐射3种传热模式。令XD为传导阶段的个体集合，XV为对流阶段的个体集合，XR为辐射阶段的个体集合，令Ns=N/3。

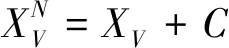
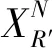
(1)

(2)

Xnew=max(Xnew,L)

(3)

Xnew=min(Xnew,U)

(4)

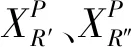
2.2 仿真验证

为验证SHTS算法寻优能力，对6个标准测试函数在5维、30维和100维条件下进行仿真实验(见表1)，并与当前寻优效果较好的TLBO算法和GWO算法的仿真结果对比，见表2。

为确保验证的公平性，本文所有验证均在Inter(R) Core(TM) i7-6500U CPU @ 2.5GHz 4GB内存的机器上实现，软件运行环境为Matlab2010b。实验参数设置：SHTS算法、TLBO算法和GWO算法最大迭代次数Gmax=200，种群规模N=100，其他参数采用各种算法默认值。为避免寻优效果的偶然性，并证明算法的稳健性，采取3种算法均对测试函数寻优20次，利用20次寻优结果的平均值、标准差对3种算法的优化性能进行评估。

SHTS算法在实验中的性能分析如下：

(1)对于单峰函数Sphere、Sumsquares、Quadric，无论是低维还是高维，SHTS算法寻优精度均优于TLBO算法、GWO算法20个数量级以上，表明SHTS算法具有较快的收敛速度和寻优精度。对于多峰函数Griewank、Rastrigin，无论是低维还是高维，SHTS算法20次寻优均获得理论最优值0，寻优精度优于TLBO算法、GWO算法(除TLBO对函数Griewank30维、100维寻优外)；对于Ackley函数，SHTS算法在5维、30维和100维实验条件下，其寻优结果相同，20次寻优结果均为8.88×10-16，标准差均为1.97×10-31，寻优精度同样优于TLBO算法、GWO算法，表明SHTS算法具有较好的全局极值寻优能力和跳出局部极值能力。

(2)对于单峰函数，随着维度的增加，3种算法的寻优精度均有所下降，尤其是TLBO算法、GWO算法，当维度达到100维时，其寻优精度低于同维度的SHTS算法44个数量级以上；对于多峰函数，无论是低维还是高维，SHTS算法寻优结果和标准差均相同，表明该算法的稳定性较好。对于TLBO和GWO算法，除Griewank函数外，其寻优精度随着维度的增加下降明显。

可见， 不论是单峰函数还是多峰函数，抑或低维或高维函数，SHTS算法的寻优精度、稳定性能均优于TLBO、GWO算法，表明SHTS算法具有较好的极值寻优能力和稳健性能。

表1 基准函数

3 混合核SHTS-SVM预测模型

3.1 混合核SVM

SVM是基于核函数原理将低维空间回归问题映射到高维特征空间进行求解，算法原理见文献[9-12]。

为进一步提高SVM预测精度，综合多项式全局核函数和高斯局部核函数二者优势，弥补二者在应用上的不足[18,22-24]，本文采用这两个函数的混合，基于libsvm工具箱构造一种满足Mercer条件的混合函数，表达式为：

Kmin=ρKpoly+(1-ρ)KRBF

(5)

式中:Kpoly=[g(x·xi)+1]3三次多项式核函数；KRBF=exp(-g‖x-xi‖2)，g>0，表示RBF核函数；ρ为权重系数。

研究表明，惩罚因子C、核函数参数g和不敏感系数ε的合理选取决定着混合核SVM性能[10]。C取值过小则易导致网络欠拟合，训练样本误差大；取值过大则网络过拟合，导致网络泛化能力差；g取值小则拟合误差小，但过小的g值会导致模型过拟合；ε值用于控制模型的预测能力，ε值小易导致模型欠拟合，ε值大则易导致模型过拟合；ρ值决定单一核函数在混合核函数中所占的比重[18]。

表2 函数优化对比结果

3.2 混合核SHTS-SVM预测实现步骤

SHTS算法优化混合核SVM关键参数有惩罚因子C、核函数参数g、不敏感系数ε和权重系数ρ，其预测实现步骤可归纳如下(多项式核SHTS-SVM、高斯核SHTS-SVM和SHTS-SBP模型预测实现步骤可参考实现)：

Step1 合理划分各算例训练样本和检验样本。设定惩罚因子C等4个待优化参数搜寻范围。

Step2 确定适应度函数。本文选用检验样本的平均相对误差绝对值之和作为适应度函数。该适应度函数描述如下：

(6)

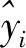
Step3 设置SHTS算法种群大小N、最大迭代次数Gmax和变量维度及变量上、下限值；设置当前迭代次数t=0。随机将种群N分成3组，并将其分配到传导、对流和辐射3种传热模式。

Step4 基于公式(6)计算种群个体适应度值，并依据适应度值确定种群中最佳适应度值f(X)和对应最佳个体X。

Step5 利用SHTS算法中传导、对流和辐射3个阶段生成新个体Xnew及适应度值f(Xnew)。

Step6 比较f(X)和f(Xnew)。若f(Xnew)优于f(X)，则Xnew代替X，Xnew进入下一次迭代；否则舍去Xnew，保留X。

Step7 令t=t+1，判断算法是否达到最大迭代次数Gmax。若达到，则输出最佳个体Xbest及所对应的个体适应度值f(Xbest)；否则转至Step5，直到满足算法终止条件，算法结束。

Step8 输出最佳个体Xbest及其所对应的个体适应度值f(Xbest)，即待优化问题的最优解及最优适应度值。

Step9 利用SHTS算法优化获得的惩罚因子C、核函数参数g、不敏感系数ε和权重系数ρ代入混合核SHTS-SVM模型进行预测。

4 算例

两个算例的参数设置均相同，即SHTS算法最大迭代次数T=200，种群规模N=100。待优化参数搜索空间设置为：惩罚因子C∈[2-10,210]、核函数参数g∈[2-10,210]、不敏感系数ε∈[2-10，210]、交叉验证参数V=5，变量维度D为4维，权重系数ρ搜索空间为[0,1]。

(1)数据来源。算例1和算例2的数据来源于云南省西洋街水文站和革雷水文站。西洋街水文站设立于1959年1月，位于云南省广南县西洋江干流上，控制径流面积2 473 km2。西洋江属珠江流域西江水系，发源于广南县者兔乡那腊村九龙山西麓，于富宁县洞巴出境进入广西田林县与驮娘江汇合，为滇桂省际河流。革雷水文站设立于1970年4月，位于云南省丘北县清水江干流上，控制径流面积3 186 km2。清水江发源于文山州砚山县者腊乡老毛山北麓，汇入南盘江，为云南、广西界河。本文利用算例1中1962-2005年、算例2中1971-2005年的实测资料进行预测分析。两个算例年径流与1-10月月均流量的相关性见表3。

从表3可以看出，算例1中，年径流与各月均流量均呈正相关关系，相关性并不十分显著。算例2中，除1月份外，年径流与各月均流量均呈正相关关系，相关性不显著。利用标准化法将算例1和算例2各径流序列数据处理在[0.1,0.9]之间。

(2)预测评价。对于算例1，选取5-10月月径流作为年径流预测的影响因子，以前30 a实测资料为训练样本，后14 a资料为检验样本；对于算例2，选取5-9月月径流作为年径流预测的影响因子，以前25 a实测资料为训练样本，后10 a资料为检验样本。分别基于MatlabR2011b软件环境创建6输入1输出和5输入1输出的年径流预测模型，选取平均相对误差绝对值MRE和最大相对误差绝对值MaxRE两个评价指标对混合核SHTS-SVM等4种模型的拟合、预测结果进行评价，见表4和图1、2。

(3)优化结果。利用SHTS算法对两个算例所有参数进行寻优计算，可以确定算例1混合核SVM惩罚因子C=28.6549、核函数参数g=2-3.4951、不敏感系数ε=2-3.2893和权重系数ρ=0.2518；算例2混合核SVM惩罚因子C=29.9799、核函数参数g=2-3.8242、不敏感系数ε=2-9.8875和权重系数ρ=0.7455。

依据表3～4及图1～2可以得出以下结论：

(1)对于算例1，无论是训练样本还是检验样本，混合核SHTS-SVM模型拟合、预测的MRE和MaxRE均优于多项式核SHTS-SVM等3种模型，其检验样本预测精度分别比多项式核SHTS-SVM、高斯核SHTS-SVM和SHTS-BP提高了57.0%、35.5%和24.2%；对于算例2，除训练样本的maxRE略低于多项式核SHTS-SVM模型外，其余训练样本的MRE、检验样本的MRE和maxRE均优于多项式核SHTS-SVM等3种模型，其检验样本预测精度分别比多项式核SHTS-SVM、高斯核SHTS-SVM和SHTS-BP提高了37.7%、26.2%和59.7%。两个算例验证结果表明，混合核SHTS-SVM模型能有效综合多项式全局核函数和高斯局部核函数二者优势，弥补二者在应用上的不足，从而提高混合核SHTS-SVM模型的预测精度和泛化能力；同时验证了本文提出的混合核SHTS-SVM模型用于年径流预测的可行性和有效性。

(2)从表3来看，算例1中年径流与月径流相关性要优于算例2，但预测效果不如算例2，其原因在于算例1中多项式全局核函数和高斯局部核函数二者互补性不如算例2。算例2中虽然年径流与月径流相关性并不显著，其最大相关系数仅为0.546，但多项式全局核函数和高斯局部核函数能很好弥补二者之间的不足，从而提升了混合核SHTS-SVM模型的预测精度和泛化能力。

表3 两个算例年径流与1-10月月均流量的相关系数

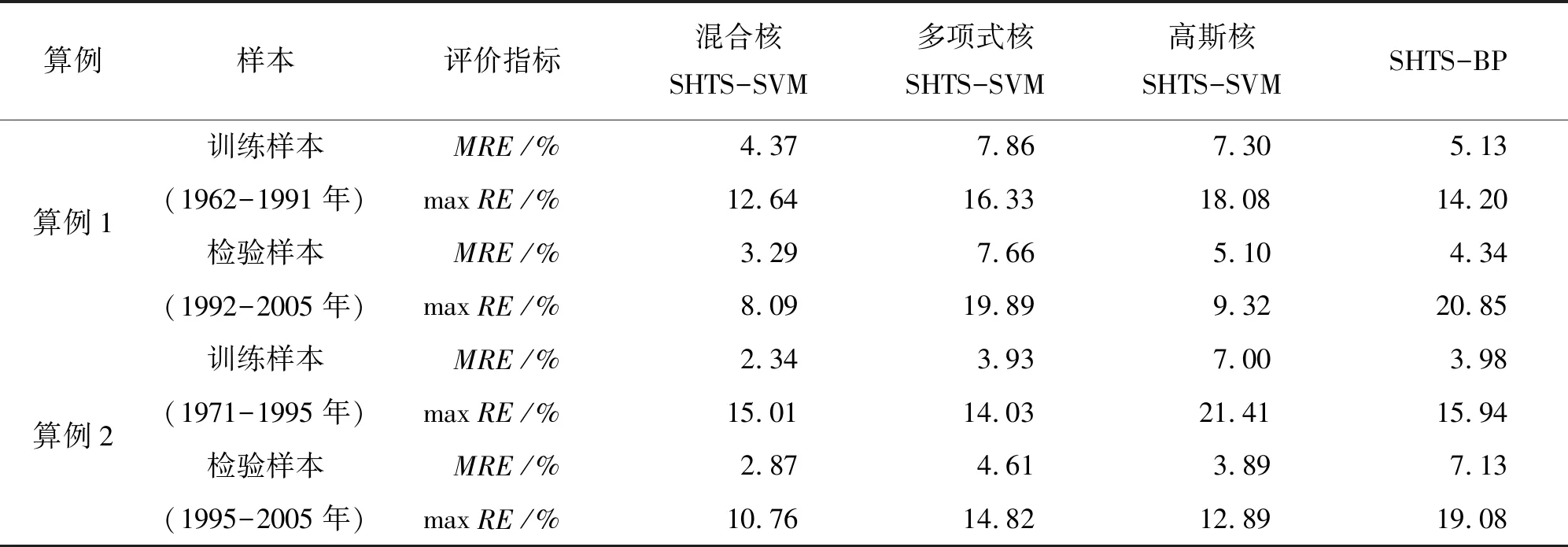
表4 年径流预测结果及其比较

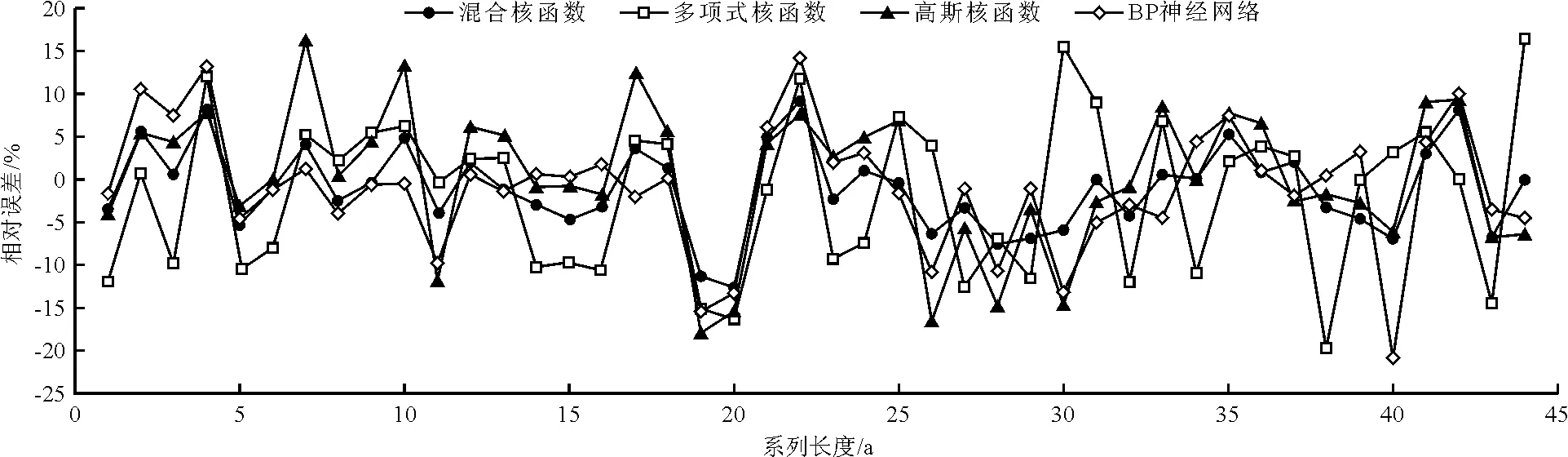
图1 1962-2005年算例1年径流拟合-预测相对误差效果图

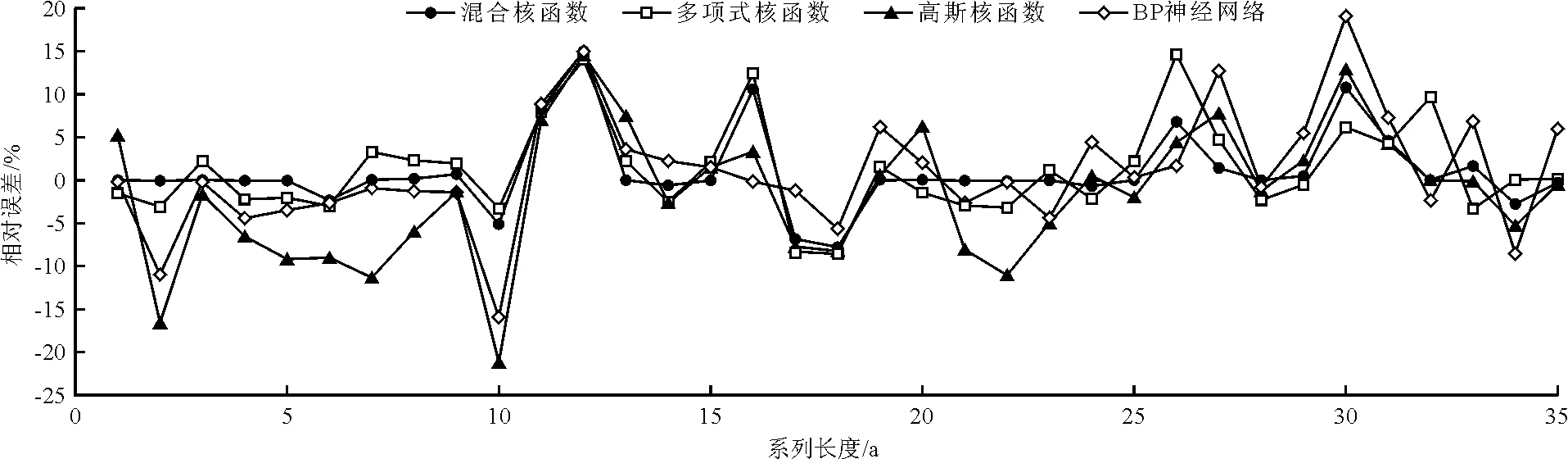
图2 1971-2005年算例2年径流拟合-预测相对误差效果图

(3)从SHTS算法对两个算例权重系数的优化结果来看，对于算例1，权重系数ρ=0.2518，表明高斯核函数占主导地位；对于算例2，权重系数ρ=0.7455，表明多项式核函数占主导地位。

(4)从图1、2及表4来看，算例1中4种模型的拟合、检验精度相差不大，4种模型均未出现“欠拟合”与“过拟合”特征。对于算例2，混合核SHTS-SVM模型、多项式核SHTS-SVM的拟合、检验精度相差不大，具有较好的预测效果和泛化能力；但高斯核SHTS-SVM模型表现出“欠拟合”特征，而SHTS-BP模型呈“过拟合”状态。

5 结 论

(1)介绍一种新型智能算法——同热传递搜索(SHTS)算法，通过6个不同维度的典型测试函数对SHTS算法进行仿真验证，并与当前寻优效果较好的TLBO算法、GWO算法作对比，结果表明SHTS算法具有较好的全局极值寻优能力和稳健性能，是一种全新高效的全局优化算法。

(2)构造线性混合核SVM，利用SHTS算法同时优化混合核SVM关键参数和混合权重系数，提出混合核SHTS-SVM年径流预测模型。利用两个算例对混合核SHTS-SVM模型进行实例验证，并与多项式核SHTS-SVM、高斯核SHTS-SVM和SHTS-BP模型的预测结果进行对比，结果表明混合核SHTS-SVM模型的预测精度优于多项式核SHTS-SVM等3种模型，表明利用SHTS算法能有效优化混合核SVM关键参数和混合权重系数；且混合核SHTS-SVM模型能有效综合多项式全局核函数和高斯局部核函数二者优势，弥补二者在应用上的不足，从而提高混合核SHTS-SVM模型的预测精度和泛化能力。

(3)两个算例验证结果表明，混合核SHTS-SVM模型用于水文预测预报是合理可行的，模型具有较好的预测精度和泛化能力，是提高预测精度的有效方法。