互相关基频检测器在平衡测试机上的应用研究

颜谋裕,李 宾,俞俊强,曾 胜

(浙江大学化工机械研究所 浙大-集智研发中心，杭州 310027)

0 引言

具有过大不平衡量的转子在旋转过程中会引起诸多问题，必须对其进行动平衡处理，其过程包含不平衡量的测量和修正。快速并准确地得到不平衡量，是修正的前提。不平衡量由影响系数矩阵和工频振动信号向量相乘得到，因此，首先要从传感器测得的原始振动信号中提取工频振动信号。原始振动信号通常是含有多种干扰频率成分的混合信号，需要用滤波器进行滤波处理[1]。

滤波器分为数字滤波器和模拟滤波器。数字滤波器采用CPU处理器对数字信号按照预先编制的程序进行计算。刘健等[2]分析比较了时域同步平均、Chebyshev窄带通滤波等数字滤波器的滤波性能和实现方法，给出了实际应用的选择依据。数字滤波对CPU处理器的性能要求较高，应用难度较大。模拟滤波器主要有二阶有源滤波器、高阶有源滤波器和具有窄带跟踪特性的开关电容滤波器等。二阶有源滤波器[3]的电路简单，设计方便，工作稳定，但频率保留范围较大，后续信号处理时间长。曾胜等[4]设计了一种可实现不平衡量快速测试的八阶有源带通滤波器，反应速度快，能有效去除高频和低频干扰，但元器件较多，存在温漂问题。江世超[5]等采用MF10开关电容滤波器，设计了具有频率跟踪的组合带通滤波器，滤波效果和元件总数与八阶有源带通滤波器相似，但避免使用电容元件，所以温漂很小。以上经模拟滤波后的振动信号都要经过整周期采样、时域平均和相关运算，进而提取出工频振动量。王丽[6]将AD633乘法器应用到平衡测试机上，但只给出了比较长的一次测试时间，没有其他相关指标数据。

本文根据互相关提取振动信号的理论，研究用简单模拟滤波器，结合硬件互相关电路和超低通滤波器，提取振动信号的方法，目的是降低总的元器件数目，快速测量并且工作稳定。

1 互相关提取振动信号的理论和方法

平衡测试机运行时，传感器输出的原始振动信号为Eu，其中不但包含不平衡量激振信号Es，还夹杂着其他频率的噪声信号En，可表示为:

(1)

取与转速同频的基准正弦信号Ers，记为:

Ers=Arsinω1t

(2)

当Eu与Ers进行乘法运算时，得到以下形式:

(3)

式(3)中，第二项为周期函数，平均值等于零。第三项为频率不同的三角函数的乘积，根据三角函数的正交性质，该项在一个周期内的积分为零，平均值也等于零。因此，将式(3)简化为:

(4)

同理，用基准余弦信号Erc与Eu相乘，可得:

(5)

工频振动信号的幅值和相位:

(6)

为实现上述过程，可用单片机产生同频基准信号Ers和Erc，分别与经过滤波的双面平衡测试机输出的两路振动信号进行互相关，下面以单路信号为例。

图1为互相关基频检测框图[6]。原始振动信号经滤波后为ES=Asin(ωt+φ)。其中，A为振动信号幅值，ω为角速度，φ为相位。单片机的D/A模块输出与转速信号同频的正、余弦信号,经滤波后得到基准正弦信号Ers和基准余弦信号Erc。振动信号Es分别与Ers和Erc相乘，经过超低通滤波器后输出的直流信号即为AR和AI，根据式(6)计算出振动信号的大小及相位。

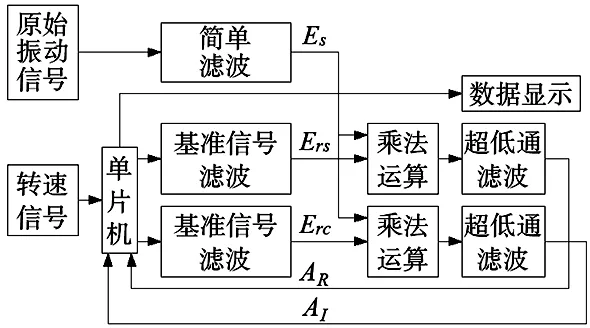
图1 单路互相关基频检测框图

图2 功能框图(AD633JN所示引脚排列)

图1中的单片机拟采用美国微芯公司生产的PIC16F1778，乘法芯片选用AD633乘法器。

2 AD633乘法器及振动信号测试方案

AD633[7]是一款功能多样、稳定性好的模拟乘法器，可方便地实现乘法、除法和开方等运算。X、Y输入端口的差动输入阻抗高达10M，能忽略信号源负载效应。AD633具有的1MHz带宽、20 V/μs的压摆率和可驱动容性负载的能力，使其广泛应用于对电路复杂性和成本要求较高的场合。

图2为AD633JN的功能框图，根据该图可得以端口名表示的传递函数:

(7)

图1的测试方案要求两路基准信号滤波电路的传递函数以及AD633的性能一致，实际调试过程难以满足这两个要求。因此，对该方案进行改进：由PIC单片机分时产生正、余弦信号，单路信号处理只用一个AD633乘法器，分时输出实部和虚部，确保电路对基准信号和振动信号的影响相同；同时，改进后的方案也可减少元器件总数。

改进后的测试方案如图3所示。

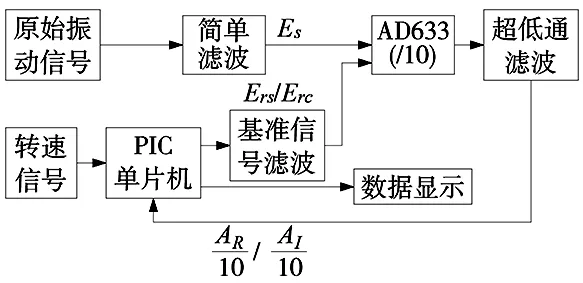
图3 改进单路互相关基频检测框图

3 信号处理电路

3.1 简单滤波电路和超低通滤波电路

由传感器输出的原始振动信号幅值小，且存在干扰，尤其是机器的固有频率，造成了原始振动信号的信噪比恶劣，对其进行信号处理可以获得信噪比合适的振动信号。阶次低的滤波电路元器件数量少，可靠性高。本文采用简单的二阶有源低通[8]和高通滤波电路[9]，根据实际平衡测试机支撑条件进行组合，对信号处理。

原始振动信号中的高、低频干扰经过简单滤波电路后被衰减。图4是简单滤波电路，通过开关可以切换电路结构为二阶(低通)或四阶(带通)，同时为使AD633X1引脚上的振动信号输入幅值适当，用放大电路进行放大。

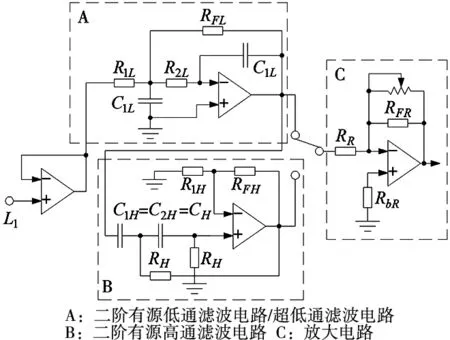
图4 简单滤波电路

二阶有源低通滤波电路的放大倍数:

(8)

电路中的R1L、R2L和RFL均取值为47kΩ，C1L和C2L取值分别为0.33μF和0.033μF，此电路作为超低通滤波电路时，选取的参数：R1L、R2L和RFL均取值为47kΩ，C1L和C2L取值均为0.47μF。

二阶有源高通滤波电路的放大倍数:

(9)

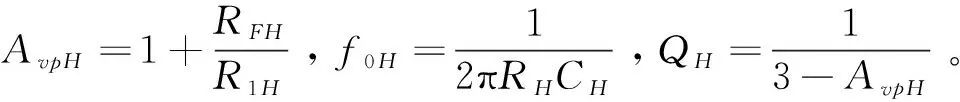
电路中的R1H、RH和RFH均取值为47K欧姆，C1和C2取值为0.1μF，4阶有源带通滤波电路的放大倍数为AvB=AvL×AvH。图5为二阶有源低通、高通、带通和超低通滤波电路的频响曲线。

(a) 幅频曲线 (b) 相频曲线 图5 二阶有源低通、高通、带通和超低通滤波电路的频响曲线

3.2 基准信号发生电路

测试过程中以PIC16F1778单片机作为基准信号发生器。转速信号由该单片机的脉冲捕捉模块CCP2捕捉。当CCP2输入引脚上出现上升沿时，记录TMR1的值，单片机立刻发送基准信号序列的第一个点，并将定时器值清零，每两个上升沿的间隔即为一转用时。取数次触发的时间间隔平均值作为当前周期，每周期输出n个点(n为4的倍数)，基准余弦曲线由基准正弦曲线左移n/4个点得到。单片机上电时，计算出正、余弦数组，预先写入存储器。定时器的值每增加一个t0(TMR1/n)，单片机输出当前时刻对应的电压。

单片机产生的基准信号，存在D/A量化带来的频率杂散，应对其进行滤波以获取平滑的基准信号。AD633运算结果会对信号造成衰减，基准信号的幅值不应太小，用放大电路对幅值进行放大。经过处理的基准信号存在直流偏移量，在末端接简单的CR高通滤波电路去除直流量。

4 性能测试

确定振动测试方案和电路结构后，搭建测试系统并进行性能测试。测试在软支撑平衡测试机上进行，不平衡量通过影响系数法[10]计算得到。软支撑平衡测试机的固有频率约为15Hz，测试时的转速频率为35Hz，输出的原始振动信号接入互相关基频检测线路板。测试时使用初始不平衡量很小的标准转子，转子质量0.59kg，校正半径20.5mm，允许剩余不平衡量40mg。

4.1 电路的性能测试

任意加试重，用数据采集卡采集传感器输出的原始振动信号、简单滤波后的振动信号和经过超低通滤波后的信号，得到图6～图8。

图6a是原始振动信号的时域图，从波形上看，信号毛刺较多；由频域图6b可看出，原始振动信号中的干扰主要来自于固有频率。而当不平衡量较小时，固有频率处的幅值会比工频振动信号的幅值大得多，信噪比更恶劣。图7a为简单滤波后的时域图，进行简单滤波后，该图的波形比图6a更平滑；从图7b的频域图可以发现此时的工频振动信号幅值较之固有频率激振信号的幅值大的多，信噪比得到了较大的改善。图8a是AD633的输出经过超低通滤波后的时域图，直流量为2206mV。从图8b可知，在进行互相关运算和超低通滤波后仍存在部分高频成分，但高频成分的幅值量很小，这些高频成分分别为20Hz，35Hz、50Hz和70Hz，幅值分别为10mV、2.5mV、2mV和3.8mV，相比于直流量非常小。其中，70Hz的信号为工频的两倍，即式(3)中的第二项，20Hz和70Hz为式(3)中的第三项，35Hz为互相关信号的部分泄漏。超低通滤波电路输出信号的频率成分与理论相符合，证明了实验方法的正确性。这些高频的信号还可以通过采样时间的平均进一步消除。

对图8的信号进行采集，依此计算出振动量和不平衡量。

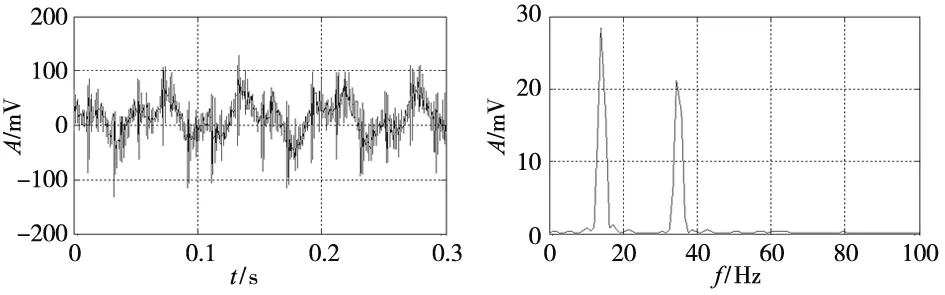
(a) 时域图 (b) 频域图 图6 原始振动信号

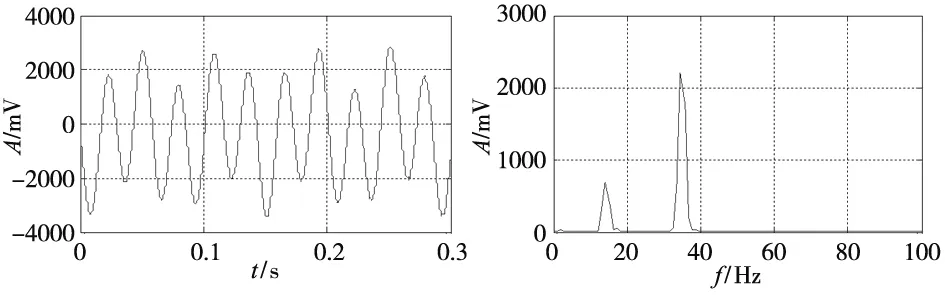
(a) 时域图 (b) 频域图 图7 简单滤波后的振动信号

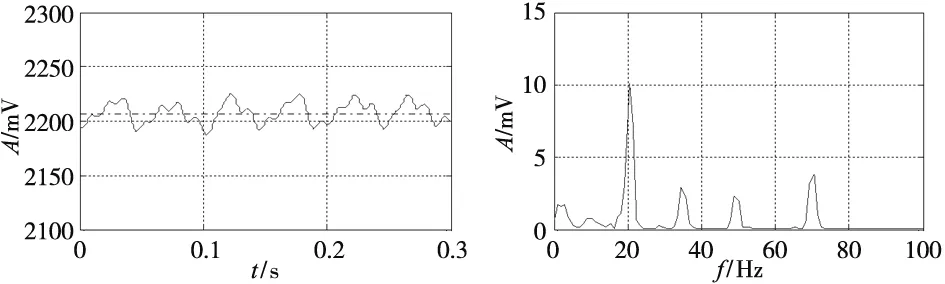
(a) 时域图 (b) 频域图 图8 超低通滤波后的输出信号

4.2 测试系统的MSA分析

为客观评价测试系统的性能，选用MSA方法[11-12]进行评估。

测试时，采样时间长度为0.5s，先测试影响系数。接着进行单次测试，得到不平衡量数据。重复进行50次测试。每次测试的运行时间为3.9s，过程包含“升速→稳速→正弦基准采样→余弦基准采样→降速→定位”等6个步骤，所得数据整理后记入表1。

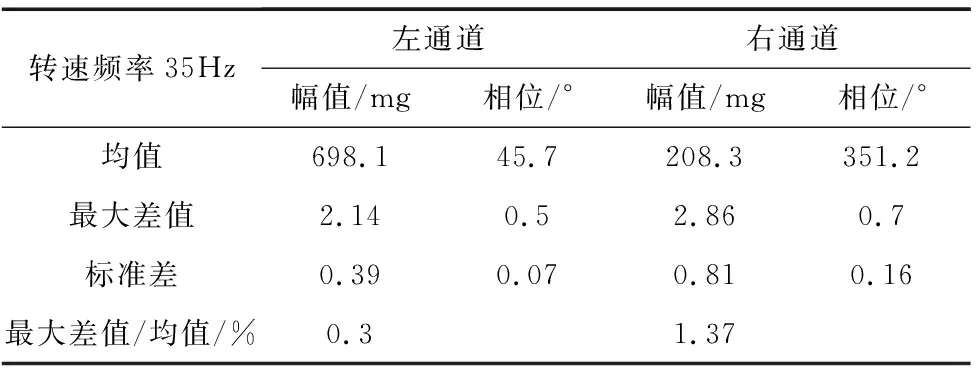
表1 不平衡量测试结果

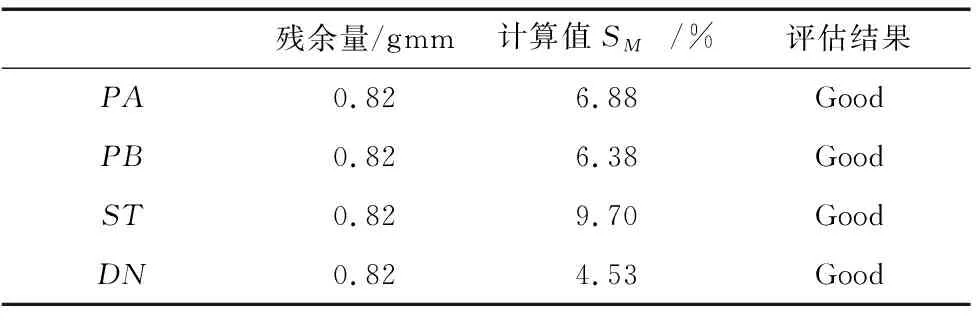
表2 测试系统的MSA评估

由表1分析，测试系统达到了幅值±1.5mg，相位±0.5°的性能，明显优于“幅值±3mg，相位±1°”的测量指标要求[4]。

表2是测试系统的MSA评估数据和结果。按照评估方法[11-12]，测试系统的PA、PB、ST、DN评估结果均为Good，性能良好。

4.3 测试系统的准确性

取1个156mg的试重放置在转子左校正面上0°位置，另1个151mg的试重放置在转子右校正面上90°位置，进行测试；更改采样时间，进行四次测试，测试结果变化范围见表3。根据表3的数据可知，采样时间大于或等于0.5s时，测试系统的面分离效果很好，可以准确识别出两个校正面上的试重。

表3 两试重分别置于两校正面0°和90°时的不平衡量测试结果

4.4 最小可达剩余不平衡度Umar

根据文献[13-14]的介绍，确定平衡测试机最小可达剩余不平衡度的操作步骤为：①将选用的校验转子初始不平衡量平衡到5Umar以下；②根据式(10)计算出试重10Upp；③将两个10Upp的试重同时、同相地分别加在左右端面间隔30°的位置，测试数据；④计算算术平均值，检验实验数据是否均满足式(11)；⑤根据式(12)估算[15]平衡测试机实际最小可达剩余不平衡度Umar估。

(10)

(11)

(12)

按照以上操作步骤，将实验参数和数据填入表4。根据表4的数据分析可知，平衡测试机的最小可达剩余不平衡度在0.15μm左右，优于市面上的多数同类机器。

表4 最小可达剩余不平衡度Umar测试数据

5 结论

本文研究了互相关基频检测器，以互相关提取振动信号理论为依据，确定了振动信号提取方案。设计了信号处理电路，制作了测试系统，进行了测试系统的MSA分析、准确性和最小可达剩余不平衡度等指标的实验。结果表明测试系统具有较好的重复性和准确性，且元器件少，可以达到“幅值±1.5mg、相位±0.5°和4s/次的测量时间”的测试水平。研究工作为硬件互相关应用到平衡测试机和自动平衡机中打下了良好的基础。