新型立体车库设计及分析

孟广耀,穆国振,王文涛,李 正

(青岛理工大学 机械与汽车工程学院,山东 青岛 266520)

随着汽车数量的增加,停车难已经成为一项急需解决的问题[1-5].在地面停车场达到满利用率的情况下,只能开发空中和地下空间,争取单位面积停车数量最大化,于是提出了九宫格式新型立体车库的概念.

根据机械行业标准[6-8],将立体车库分为升降横移、垂直循环、水平循环、多层循环、平面移动、巷道堆垛、垂直升降和简易升降共8类.目前,市场上采用最多的是垂直循环类,但由于立体车库的缺点较多,未能普及,停车难的问题依然存在.因此,立体车库的改革创新对于解决停车难的问题具有重要意义.本文提出一种新型立体车库,对安全性、空间利用率和存取便捷度进一步优化.

1 新型立体车库设计[9]

1.1 新型立体车库设计思路

新型立体车库是在传统立体车库基础上创新,保证立体车库基本功能,最大化空间利用率,且存取车更便捷.

传统立体车库单个载车板移动为2个方向,如图1所示,单个载车板须预留一个存取车通道实现存取车,空间利用率降低.为增加立体车库空间利用率,减少载车板预留通道,提出单个载车板实现4个方向移动的概念,增加空间利用率,除C3为升降机构外,其余为载车板停车位,单个载车板能实现4个方向移动.

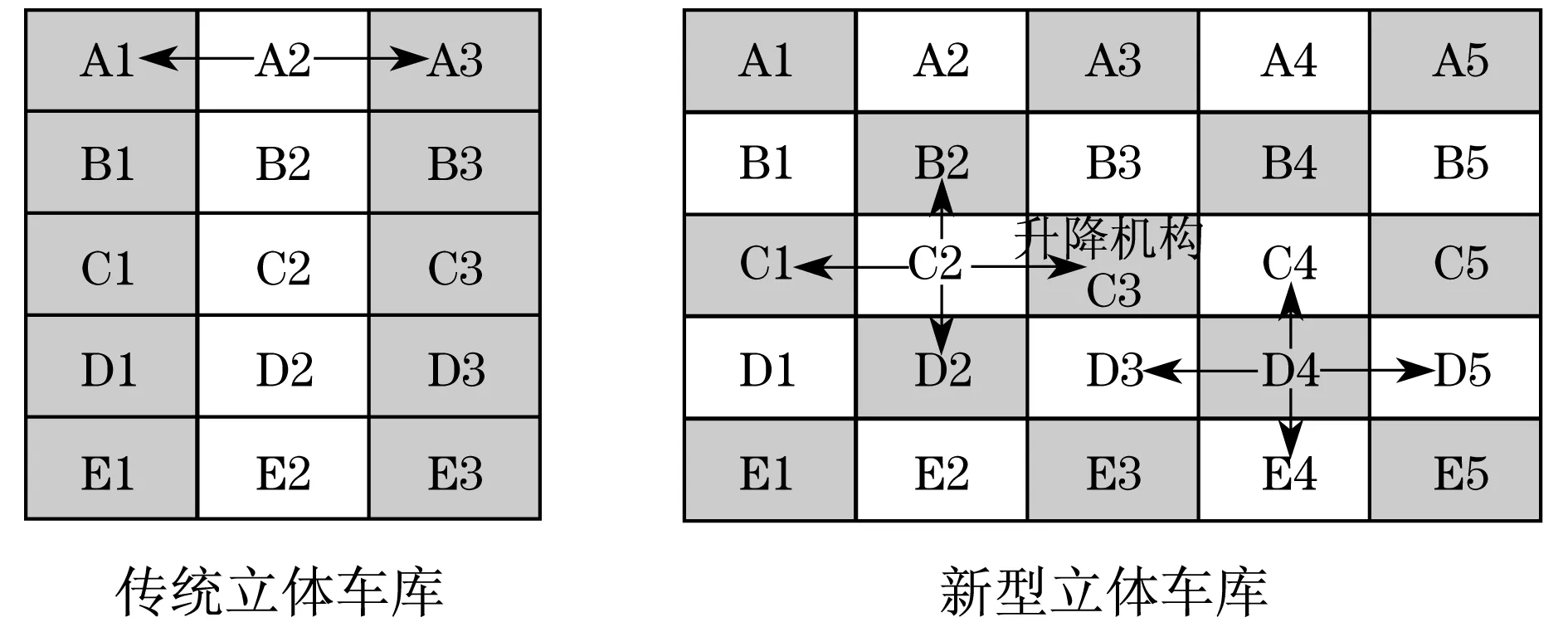
图1 立体车库载车板移动方向示意图Fig.1 Diagram of moving direction of carboard in stereo garage

九宫格式立体车库通过单层的水平横移配合升降机的上下升降来实现车辆的存取动作.区别于传统二维立体车库,九宫格式立体车库为三维立体车库(X,Y,Z),其存车总数量为

(1)

式中:X为单层车辆行数;Y为单层车辆列数;Z为车库层数;C为载车板存取机构数量.

1.2 新型立体车库结构设计

根据标准[6-8]确定立体车库停车尺寸为5 500 mm×2 200 mm×1 950 mm.对实现4个方向的移动的载车板进行传动装置设计,采用辊筒传动,其传动方案如图2所示.

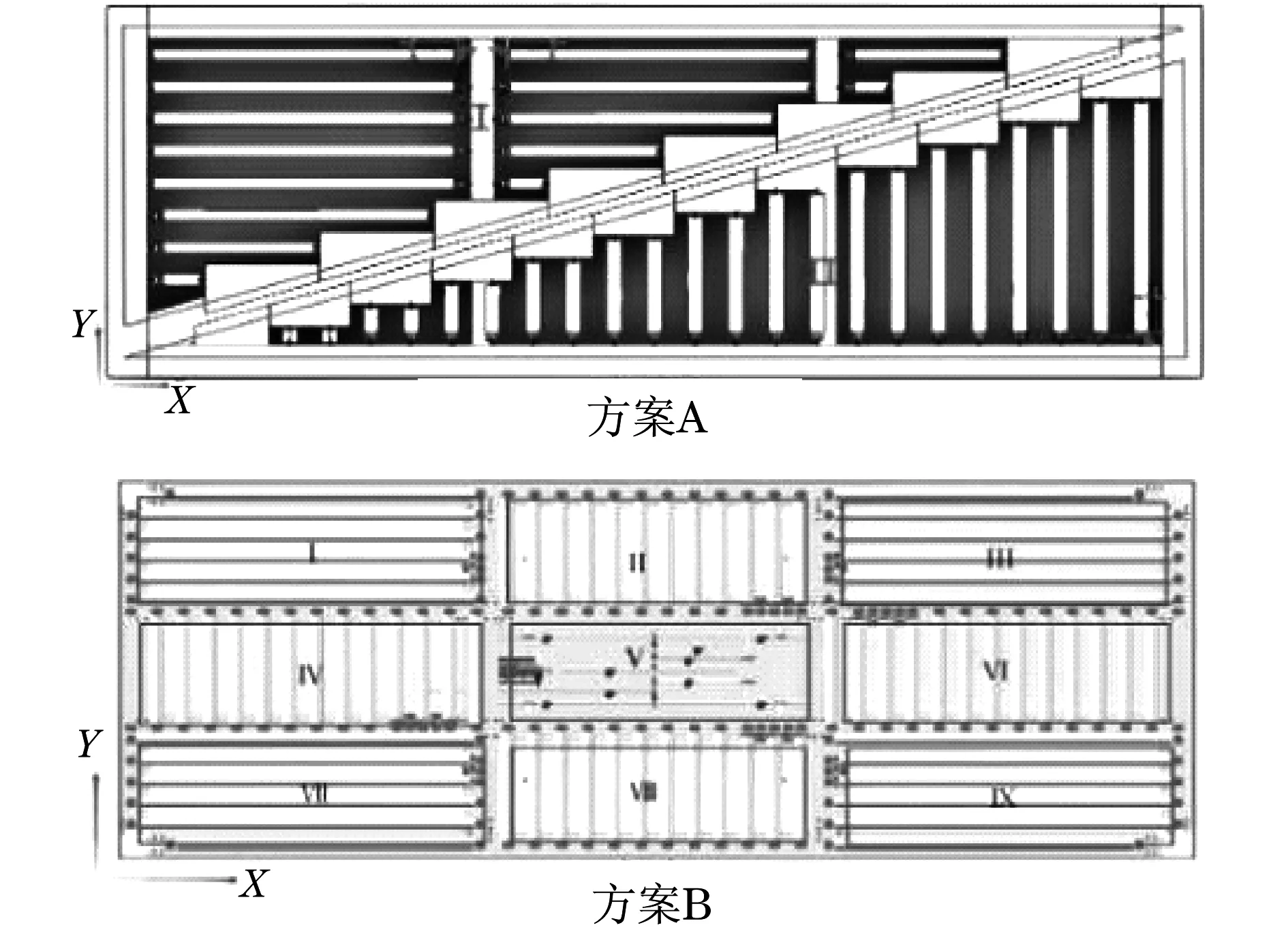
图2 传动机构辊筒位置方案Fig.2 Transmission mechanism roller position scheme

方案A与方案B框架尺寸相同,均能实现载车板4个方向移动.方案A把单个传动机构分为2个三角形区域Ⅰ和Ⅱ,Ⅰ区域负责Y,-Y方向,Ⅱ区域负责X,-X方向,未预留传动装置空间;方案B把单个传动机构均分为9个区域,Ⅴ区域为传动装置预留区域,Ⅰ,Ⅲ,Ⅶ,Ⅸ区域负责Y,-Y方向,Ⅱ,Ⅳ,Ⅵ,Ⅷ区域负责X,-X方向移动.

在基本功能均能实现的前提下,考虑传动结构强度、载车板传动稳定性、空间分布合理性,采用方案B进行传动机构设计[9].

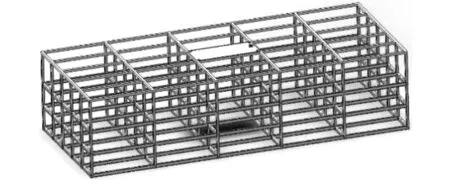
图3 立体车库钢结构装配图Fig.3 Steel structure assembly drawing of stereo garage

方形冷弯空心型钢许用应力[σ]=113 MPa,满载情况下,假设车辆和载车板质量为MG=3.5 t,每个辊筒传动装置总H型钢长度为15.4 m,每根立柱共承受3层平台,每层平台共4个车位.

每个辊筒传动装置的H型钢质量为

(2)

式中：MD为H型钢单位质量.

平台横梁分为滚筒传动平台外围5 500 mm,2 200 mm和内部1 700 mm支撑梁3种.3种横梁的质量分别为

式中：MH1，MH2，MH3分别为3种不同型钢质量；LH1，LH2，LH3分别为3种不同型钢长度.

每个辊筒传动装置质量(MO:辊筒、轴承等质量)为

(6)

每个螺栓与方形冷弯空心型钢接触面积为

(7)

应力为

(8)

应力与许用应力比较,即

(9)

通过比较分析,方形冷弯空心型钢满足立体车库满载时强度要求.

纯弯曲变形的正应力分析,综合考虑变形几何、物理和静力3方面,型钢的弹性模量为2.1×107N/cm2.

纵向纤维的应变与它到中性层的距离成正比，即

(10)

式中：ρ为中性层的曲率半径；y为任意纵向纤维至中性层的距离.

任意纵向纤维的正应力与它到中性层的距离成正比,即

(11)

式中：E为弹性模量.

根据平衡方程,弯矩M与外力偶Mz大小相等,方向相反,即

(12)

式中：Mz为关于z轴的外力偶.

纯弯曲时,梁横截面上弯曲正应力的计算式为

(13)

也可以写成

(14)

式中：Iz为z轴的惯性矩.

弯曲正应力的强度条件为

(15)

式中：W为抗弯截面模量.

对5 500 mm横梁,可得相应参数为

(16)

(17)

σmax|5 500=91.96 MPa≤[σ]=113 MPa

(18)

对2 200 mm横梁,可得相应参数为

(19)

(20)

σmax|2 200=14.71 MPa≤[σ]=113 MPa

(21)

对1 700 mm横梁,可得相应参数为

(22)

(23)

σmax|1 700=8.79 MPa≤[σ]=113 MPa

(24)

根据以上计算和分析比较,3种横梁在满载时的强度达到国标要求.

在对弯曲变形的讨论时,x为变形前横梁轴线,y为垂直向上的轴,xy面为横梁的纵向对称面.在对称弯曲的情况下,横梁变形后将成为xy平面内的一条曲线,成为挠曲线.在挠曲线上横坐标x任意一点所对应的纵坐标用w表示,成为挠度,代表x横截面的形心沿y方向的位移,挠曲线的方程可以写为

(25)

弯曲变形中,横梁的横截面相对原来位置转过的角度θ成为截面转角,有

纯弯曲下,弯矩与曲率之间的关系为

(28)

将

带入式(28)得

带入式(31)得

(33)

因为在小变形情况下,w=f(x)是一跳平坦曲线,转角θ也是一个非常小的角度,所以

(34)

(35)

对其两边乘以dx,积分得到转角方程为

(36)

对其两边乘以dx,积分得到挠曲线方程为

(37)

刚度条件如下:

|w|max≤[w]

(38)

|θ|max≤[θ]

(39)

计算横梁的支座约束力,写出弯矩方程,利用式(37)积分两次,得

式中：q均布载荷；l为模梁长度.

假定一端固定,故x=0时，w=0.

于是

在挠曲线中点,切线斜率为0,挠度为极值,可求得

(44)

式中：I为材料横截面对弯曲中性轴的惯性矩.

横梁两端的截面转角数值大小相同,符号相反,绝对值最大,于是当x=0和x=l时,得

(45)

式中：θA，θB为变形角度.

对5 500 mm横梁,分为3个均等空间,每个空间参数如下:

对2 200 mm横梁,分为3个均等空间,每个空间参数如下:

根据以上计算,横梁最大挠度即纯弯曲变形符合手册参数.

2 新型立体车库ANSYS分析

新型立体车库确定结构后,对其进行ANSYS静态学分析,以确定满载状态下车库的总变形;对其进行模态分析,以确定固有频率;对其进行随机振动分析,以确定稳定性.

2.1 静态学分析

立体车库STEP文件导入ANSYS,选材为Structural Steel,自动网格划分,立体车库底面为固定约束,72个载车板单个受力25 000 N.静态学分析结果如图4所示.

图4 新型立体车库静态学分析总变形Fig.4 Static analysis of total deformation of new type stereo garage

从图4可知:新型立体车库总变形从底层到高层逐步增加,底层较大变形载车板为围绕升降装置的8个;中层和高层所有载车板均有较明显变形,最大变形出现在高层边缘载车板,最大变形量为0.157 26 mm,符合立体车库设计标准[6-8].

2.2 模态分析

为确定新型立体车库的固有振动特性,避免在特定频率下新型立体车库的共振,对其进行模态分析.

新型立体车库的前6阶模态振型分析结果汇总如表1所示,频率折线图如图5所示.

图5 模态结果折线图Fig.5 Modal result line graph

表1 新型立体车库前6阶模态分析结果汇总Tab.1 Summary of the first 6 order modal analysis results of new stereo garage

模态分析结果表明:新型立体车库的频率范围为5.723 7～13.390 0 Hz,应避开此频率区域工作,以免共振发生.新型立体车库前3阶固有频率在7 Hz以下,振型以整体倾斜为主,变形量在0～2.761 2 mm范围内.第4阶、第5阶固有频率在12～13 Hz,振型以高层变化为主,出现扭曲状,变形量在0～5.428 0 mm.第6阶固有频率为13.390 0 Hz,振型以整体弯曲为主,变形量在0～2.597 1 mm.分析可知,新型立体车库结构设计较合理,满足立体车库正常的存取需要.

3 结论

(1) 根据市场需求,结合现有立体车库经验,进行新型立体车库概念设计,得出概念想法.

(2) 通过新型立体车库概念想法,结合立体车库功能实现方式,设计出运动机构,实现存取车动作.

(3) 通过对立体车库局部结构校核计算,得出设计安全性结论.

(4) 依据新型立体车库结构图,运用AYSYS Workbench进行静态学、模态和随机振动分析,得出新型立体车库的安全可行性.

(5) 综合九宫格式新型立体车库设计及分析,发掘一种新型思路,对传统立体车库的创新发展具有一定的意义.