地铁列车运行振动对车站及上部建筑沉降影响数值模拟研究★

祁晓雨 殷雪宁 梅 钢 张兹钰 涂劲之

(中国地质大学(北京)工程技术学院，北京 100083)

1 概述

随着现代工业的迅速发展和城市规模的日益扩大,我国地铁运输系统迅猛发展，地铁的高速运动给人们的出行带来方便的同时，地铁产生的振动也对地铁站以及沿线周围建筑物产生了影响，例如地铁高速运动与轨道之间的摩擦可能导致轨道变形或磨损，地铁振动会使相关地表建筑结构发生变形甚至开裂等，将会产生不可估测的安全隐患。振动对大都市生活质量和工作环境的影响引起了人们的普遍注意。国际上已把振动列为七大环境公害之一[1],如何控制振动所带来的对地铁运营安全、地铁使用寿命、相关联的地表建筑结构的安全隐患成为一个亟待解决的重要课题。

林永国等[2]从施工、地质和外界扰动等多方面分析了影响地铁隧道纵向变形的因素；韩煊、李宁[3]采用数值分析方法研究了隧道衬砌在土水压力的作用下,断面所产生的椭圆化变形引起的地层位移规律,指出衬砌受压变形造成的地层位移是地表沉降槽曲线偏离高斯分布规律的重要原因之一；方浩亮，迟明等[4]以青岛地铁3号线为工程实例，借助FLAC3D与现场监测数据对地表沉降及其收敛变形进行研究，得出了隧道地表沉降及净空收敛的规律。

本文拟分析建成的地铁车站在排除自重变形因素影响后，对列车振动引起地铁车站及上部建筑发生沉降进行研究。首先，采用MIDAS GTS软件构建地铁车站数值计算模型；之后，导入FLAC3D软件计算地铁列车运行振动对地铁车站及上部建筑造成的沉降；最后，通过分析沉降位移曲线的特征，得出地铁列车运行振动对地铁车站及上部建筑沉降的影响。研究结果对地铁的运营和维护具有意义。

2 计算模型和计算参数

2.1 模型的建立

下面以地下2层标准岛式车站为例。运用MIDAS GTS软件建立模型，该模型主要分为三部分：地层、地铁车站、地上建筑。考虑到边界效应，模型尺寸定为120 m×90 m。地表面为自由面，其余面增加相应的边界条件。模型如图1所示。

将建立的模型导入FLAC3D软件，运用有限差分法进行数值分析。模型采用了四面体网格(brick)组合而成，采用的摩尔—库仑塑性本构模型的材料参数包括:密度 density(ρ)、弹性体积模量bulk(K)、弹性剪切模量 shear(G)、粘聚力cohesion(c)、内摩擦角friction(φ)、抗拉强度tension(σt)、泊松比poisson(μ)。它们之间的转换关系如下:

(1)

(2)

为使计算结果可靠，对本例中的模型做出以下假设条件：

地铁振动的初始条件为：

1)地铁车站已建成，原始地层固结沉降已完成。

2)地层土体均采用摩尔—库仑塑性本构模型，只考虑重力作用。

3)边界条件: 模型基底约束竖向(Z)位移，地铁车站走向的两个端部断面约束Y方向位移，X方向的两个端部断面约束X方向位移。

由地铁列车运行振动产生的动力条件为：

1)本例在模型周围施加自由场边界，同时在模型底部施加静态边界条件。

2)设置局部阻尼，对于岩土材料，有：

αL=πD。

其中，αL为局部阻尼系数；D为临界阻尼比。

临界阻尼比一般取0.05，则局部阻尼系数可取0.157。

3)振动方向是X，Z轴方向，作用时间为10 s。

2.2 参数的取值

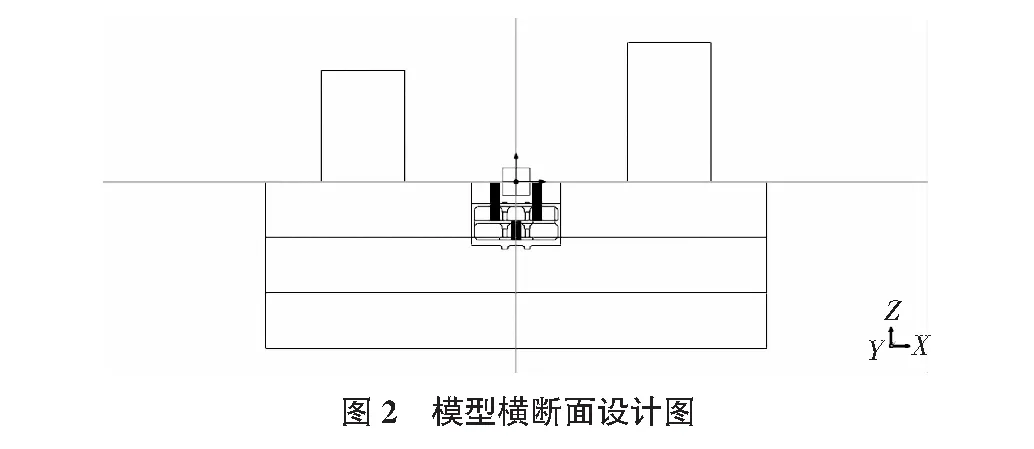
本例中模型的参数根据实地的调查、查阅GB 50157—2013地铁设计规范，设置该车站底板埋深为11.5 m，车站高度为7.5 m，维护层厚0.5 m，底板厚1 m，方柱边长0.8 m，其上部连接不规则扩大部分；有四个出入口，连通的地下1层为检票进站层，地下2层为候车乘车层；设置四座楼梯。模型横断面尺寸见图2。

根据北京地区的工程地质条件，地下土体大致分成粉质黏土层、黏土层、风化岩层，三者厚度均为10 m，并根据相关资料查找到土层性质参数见表1。

表1 地层土体参数取值

3 数值模拟结果分析

3.1 数值计算结果

将模型导入FLAC3D软件，分别对仅自重条件下和在列车运行振动影响下进行数值分析，得到以下结果。

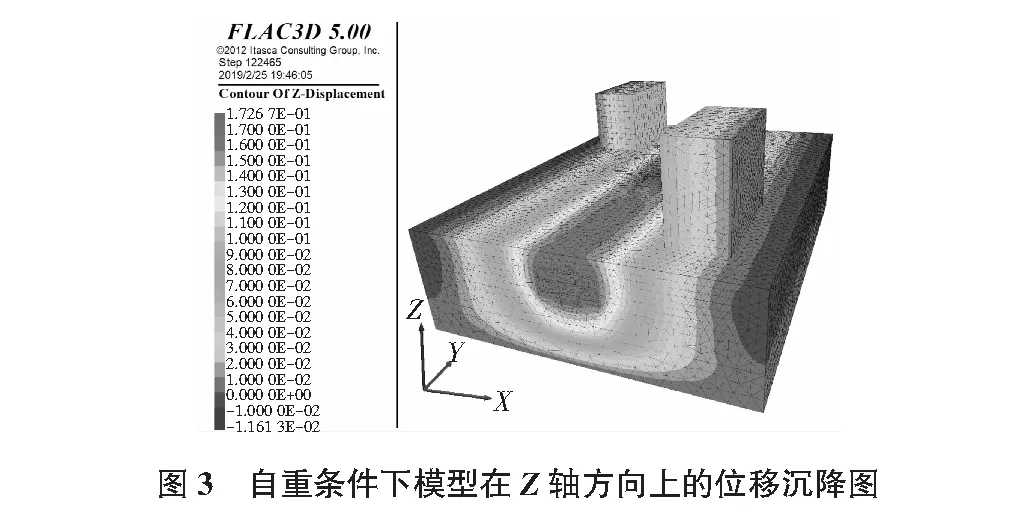
仅自重条件下模型在Z轴方向上的位移沉降云图见图3。

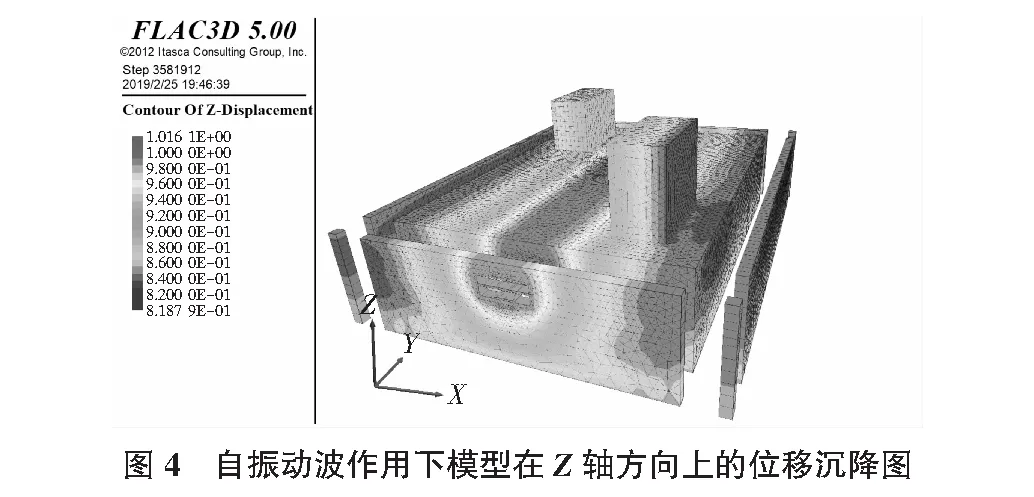
列车运行振动影响下模型在Z轴方向上的位移沉降云图见图4。

仅由振动引发的车站与周围地层的沉降以及地上建筑的变形Z可用下式表示：

Z=Z2-Z1。

其中，Z2为列车运行振动影响下地铁车站与地上建筑沉降量；Z1为仅自重作用下地铁车站与地上建筑变形量。

3.2 计算结果的分析

取地铁车站顶部和底部共12个外侧点、地上建筑物底部共8个角点、横截面上每隔5 m剖分地层设置监测点，记录不同埋深下的地层在Z轴方向上的沉降位移、地铁车站以及地上建筑的沉降位移，由计算结果如图5，图6和表2，表3所示。图5，图6中纵坐标正值表示沉降方向朝Z轴负方向。

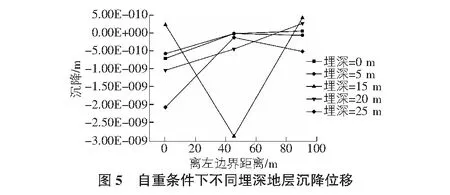
表2 西、东侧建筑物沉降位移

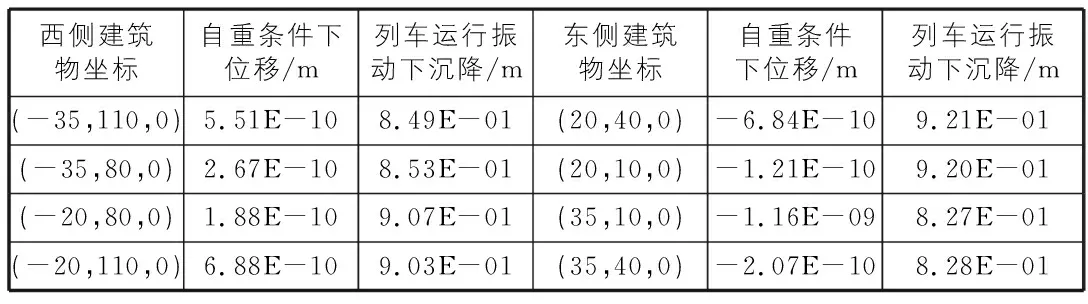
西侧建筑物坐标自重条件下位移/m列车运行振动下沉降/m东侧建筑物坐标自重条件下位移/m列车运行振动下沉降/m(-35,110,0)5.51E-108.49E-01(20,40,0)-6.84E-109.21E-01(-35,80,0)2.67E-108.53E-01(20,10,0)-1.21E-109.20E-01(-20,80,0)1.88E-109.07E-01(35,10,0)-1.16E-098.27E-01(-20,110,0)6.88E-109.03E-01(35,40,0)-2.07E-108.28E-01

可以看出，自重条件下地层位移产生负值是由于边界的存在，模型中部的土层向下沉降导致边界附近的土层受到挤压而具有向上的位移，而且位移量很小。总体来说，随着埋深的增加，地层沉降位移先增加后逐渐减小，且越靠近边界土层越“膨胀”。在自重条件下，东西两侧建筑物的沉降位移越靠近边界越大，地铁车站随埋深的增加，车站中部沉降位移越大，因而挤压下伏土层使其往两边上移，对车站角点附近的围护结构起到向上托举作用。地铁运行振动时，模型各个部分的沉降位移有了明显向下增加的趋势，从地层上看，地表沉降量最大，向下增加埋深，位移沉降量呈递减趋势；东西侧建筑物底部和地铁车站的沉降量相对于自重条件下有了明显增加。

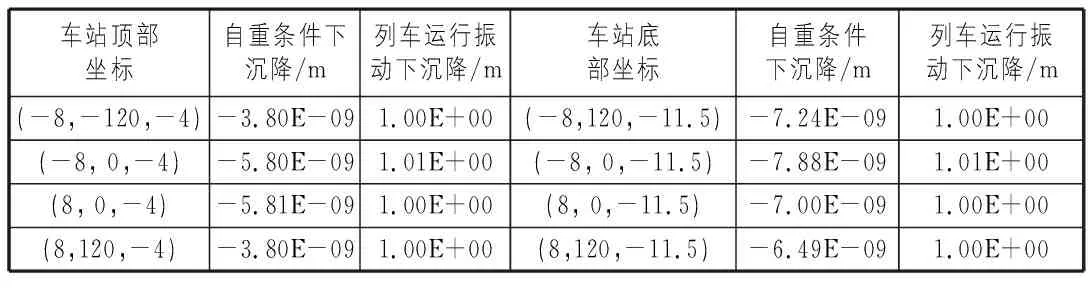
表3 地铁车站顶、底部沉降

经过计算差值，得出仅在列车运行振动影响下模型的沉降位移结果如图7和表4,表5所示。

表4 仅振动影响下西、东侧建筑物沉降位移

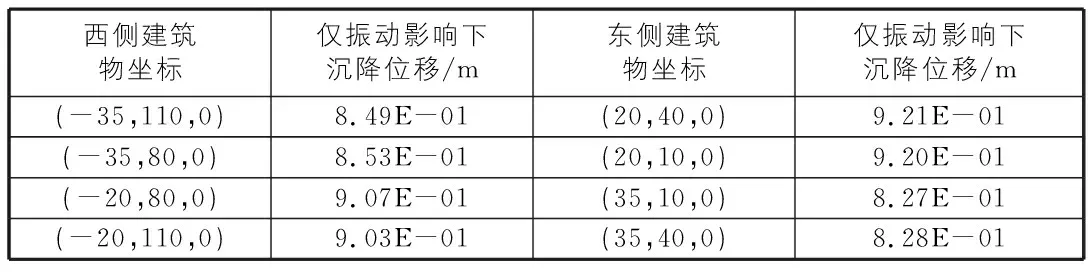
西侧建筑物坐标仅振动影响下沉降位移/m东侧建筑物坐标仅振动影响下沉降位移/m(-35,110,0)8.49E-01(20,40,0)9.21E-01(-35,80,0)8.53E-01(20,10,0)9.20E-01(-20,80,0)9.07E-01(35,10,0)8.27E-01(-20,110,0)9.03E-01(35,40,0)8.28E-01

表5 仅振动影响下地铁车站顶、底部沉降

由以上差值图表可知，由于自重产生的沉降位移量是极小的，振动的产生是使地层发生沉降和建筑物变形的主要原因。整体上靠近地下车站附近的地层沉降量最大，随着埋深增加地层沉降量递减；东西两侧建筑物的沉降位移越靠近地下车站的中轴线越大；地下车站沿着隧道走向上中间部分的位移沉降量最大，越往两端位移沉降量逐渐减小。

4 结论

本文采用MIDAS GTS软件构建地铁车站数值计算模型，导入FLAC3D软件计算地铁列车运行振动对地铁车站及上部建筑造成的沉降，获得了仅自重条件下和在列车运行振动影响下的沉降位移曲线，并得出以下结论：

1)自重产生的沉降位移量的影响是极小的，但是会造成地下车站中部向下沉降，从而挤压下伏土层使其往两边上移，对车站角点附近的围护结构起到向上托举作用。

2)列车运行振动是使地层和建筑物发生沉降的主要原因，距轨道中心线越近，列车引起的地面振动越大，随着距离的增加而有较大的衰减，超过一定距离衰减变缓。结果显示地下车站附近的地层沉降量最大，且随着埋深增加地层沉降量递减。还会影响地上建筑物，建筑物越靠近地下车站的中轴线位移沉降越大，可能导致建筑物向中轴线方向倾斜或者产生沉降裂缝。

3)列车运行振动对地下车站的影响最大，沿着隧道走向上中间部分的位移沉降量最大，越往两端位移沉降量逐渐减小，可能造成地下车站的不均匀沉降，从而对地铁运营安全、地铁使用寿命有不利影响。

通过对地铁车站及其地上建筑进行三维建模，针对地铁车站及地上建筑结构进行空间、时间上的研究，模拟地铁运行过程，研究地铁运行产生的振动对地铁车站结构变形的影响，以达到预测并防止地铁车站损坏、开裂等工程事故，保证地铁安全运营的目的，延长地铁车站的寿命，保护地上建筑。通过数值模拟和有限差分的方法，可以避免传统实地预测实验的复杂性与可变性大等缺点。但本文所采取的模型仍有许多值得改进之处：a.地铁车站可采用更加精细的支护模拟以更加接近真实工况；b.在靠近地下车站附近的地层的厚度、物理性质等参数取值，对列车运行引起的地面振动有较大的影响。这些问题将在以后的研究工作中逐步完善。