Ti 及中间温度对双相钢强度影响规律研究

冯啟萍

（青海西宁特殊钢股份有限公司，青海 西宁 810005）

引言

双相钢（DP 钢）指由低碳或低合金钢经临界区热处理或控轧控冷而得到的由铁素体相和马氏体相组成的高强钢。双相钢具有低屈强比，较高的初始加工硬化速率和延性强度匹配良好等特点，在汽车工业领域得到了广泛的应用。根据超轻钢车体（ULSAB）组织预测，双相钢占汽车钢的比例将达到70%以上。双相钢的这些力学性能特点也吸引了大批学者对其进行解析和研究。

其中，有学者指出双相钢的抗拉强度符合混合物定律，即双相钢的抗拉强度与马氏体体积分数呈线性关系，这为双相钢的强度预测提供了一个可行性的方法。但由于双相钢中存在较多强化机制（细晶强化，固溶强化，析出强化、相变强化等）的综合作用，以往利用混合物模型预测双相钢强度时，往往只考虑了晶粒的细化和微合金元素固溶的影响，而忽略了第二相在铁素体基体中析出强化对其强度的贡献，造成了预测值和实测值之间有较大的误差。

在双相钢的生产中，加入少量的微合金元素（如Nb，V，Ti）可以大幅度的提高产品的强度。其中，Ti 的成本较低，且具有改善钢的冷成形性能和焊接性能等特点，日益引起人们的重视。

本文基于混合物定律法，采用Thermo-Cal V5.0 热力学软件进行双相钢抗拉强度的计算。该方法进一步考虑第二相析出强化的贡献，完善了双相钢强度的预测模型，利用完善后的模型分析讨论了不同Ti 元素加入量和不同中间温度对双相钢强度的影响。

1 双相钢强度预测模型优化

铁素体和马氏体是双相钢的构成相，由于两相性能上的差异，因此在塑性变形时两相在不同变形阶段表现出不同的应力和应变分布。虽然有学者建立了一些应力应变模型，但迄今为止对于应力应变在两相中的分配情况并没有一个较好的解释。这也使得通过流变理论计算双相钢的强度变得困难。根据混合物定律，双相钢的抗拉强度可以用如下表达式进行计算：

式中 σb为双相钢的抗拉强度，分别为铁素体和马氏体的抗拉强度。 VM、 VF为马氏体和铁素体的体积分数。需要注意的是，由于混合物定律忽略了马氏体形状和空间分布对双相钢的影响，其预测的流变应力通常是正确值的上限。

在以往的研究中铁素体屈服强度一般采用Hall-Petch 公式计算。

研究表明，低碳钢的抗拉强度比屈服强度高出约69MPa，假设铁素体的强度不受碳含量的影响，其抗拉强度可以表示成：

其中， 为晶格摩擦力， 为常数，根据文献将，， 分别取值为49MPa 和500MPa。研究表明，在低碳微合金钢中，0.1～0.2 vol%的2～5nm 的碳氮化物析出粒子可以使强度增加200～400MPa，因此析出强化也是双相钢的一种主要强化机制，不可忽略其影响。Orowan 公式是计算第二相粒子析出强化作用的经典公式，其表达式如下：

式中，yσΔ 为沉淀强化贡献的屈服强度；X 为第二相粒子直径；G 为切变弹性模量，b 为柏氏矢量；f 为析出相粒子的体积分数。文献中表明，常用G、b 值分别为80650MPa 和0.248nm。Arsenault 等人提出在计算多种强化机制并存的金属材料强度时，可以简单的利用混合强化模型来计算其复合强化效果，即把各种单一的强化作用线性叠加起来。因此，改进的铁素体抗拉强度模型可以表达为：

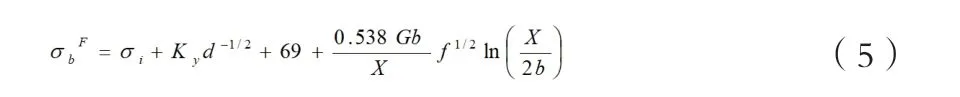
可以看到，公式（5）中同时考虑了细晶强化和析出强化的共同作用对铁素体抗拉强度的影响。而马氏体的抗拉强度主要由其含量碳决定，所以公式（1）中可以根据经验公式计算：

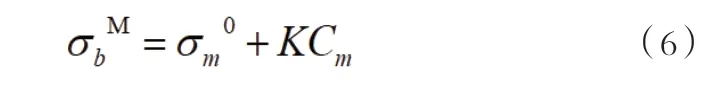
2 Thermo-Cal 软件在双相钢强度计算中的应用

Thermo-Cal 热力学计算软件集成了热力学、动力学等多个模块，经过长期的发展其热/动力学数据库较为完善，同时该软件功能齐全，被世界上众多学者广泛用于材料成分设计、析出相计算、相变动力学计算等方面的研究。该软件在世界上享有相当声誉且已成功应用于钢种的研发。

本文利用Thermo-Cal 软件计算高温时双相区的相组成，通过高温双相区奥氏体的体积分数和含碳量估算淬火后马氏体的体积分数和碳含量。同时，利用Thermo-Cal软件计算析出相的体积分数和相组成元素。将结果代入混合物模型对双相钢强度进行计算分析。本文所研究双相钢中铁素体直径取10um，析出相直径取5nm。

表1 实验用双相钢化学成分成分

3 不同Ti 含量对双相钢析出行为和抗拉强度影响的Thermo-Cal 计算与分析

在实际生产中，双相钢中马氏体的体积分数均低于25%，过高的马氏体量会导致力学性能的下降。现设所研究双相钢中马氏体体积分数为20%，同时利用Thermo-Cal 软件计算并分析Ti 质量分数在0～0.12%变化区间内双相钢的析出行为和抗拉强度的变化。

由图1 可知，当铁素体转变量为80%，随着Ti 含量的增加转变完成温度不断升高，由不添加Ti 时的T1=732 ℃升高到0.12%Ti 时的T2=758 ℃。这说明Ti 能加速铁素体的生成，使其在较高温度即完成所需转变量。这是由于在 转变过程中铁素体的排碳作用逐渐使铁素体相和奥氏体相形成了较高的碳浓度差，阻碍了铁素体转变，Ti 的加入结合了一部分碳并以碳氮化物的形式析出，降低了奥氏体一侧的碳浓度，增大了铁素体转变的驱动力，因而促进了铁素体转变。此外，由图2 可知，Ti 含量的增加，也提高了析出相的体积分数，每增加0.01%Ti 便会析出约0.02%体积分数的碳氮化物。

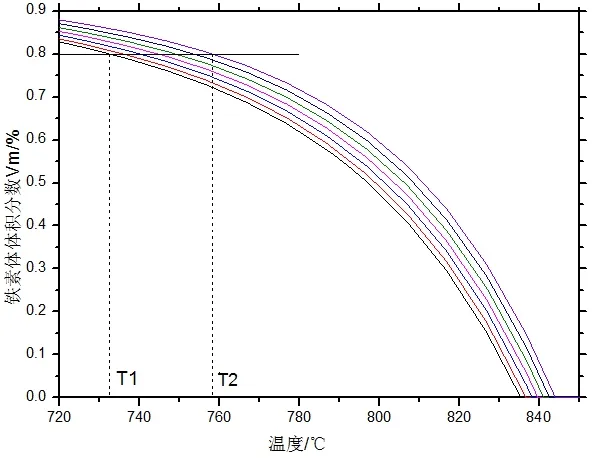
图1 不同Ti 含量下铁素体转变量随温度的变化

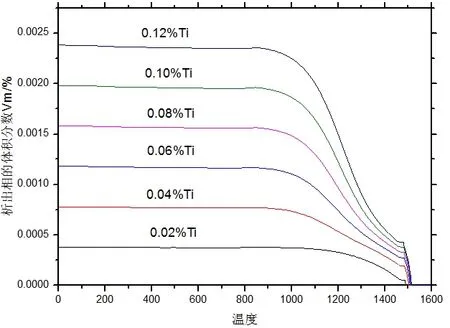
图2 不同Ti 含量下析出相体积分数随温度的变化

另外，从析出相的元素组成分析，Ti 含量不同，析出相的组成也不同，从图3 可知，Ti 含量对析出相中Ti的占位数影响不大，其始终稳定维持在0.75～0.8 范围，而对析出相中的C、N 的占位数有着较大的影响。当Ti含量为0.02%时，C、N 在碳氮化物中的的占位数分别为0.19 和0.03，析出相主要为TiN，其中Ti/N 比为约4 接近理想化学配比（3.4），在此化学配比下TiN 具有较强的抑制奥氏体晶粒长大的作用。当Ti 含量增加至0.06%时，析出相中C、N 的占位数随温度发生了较大变化，高温时（≥1250℃），N 的占位数高于C，析出相为TiN，随着温度的降低，N 的占位数逐渐下降，由0.2 降为0.065，C 的占位数则由0.01 升高到0.14，并在1000℃以下趋于稳定。此时Ti/N 约为12，远高于理想配比，多余的Ti 在与C 结合后以TiC 形式析出。当Ti含量升高到0.12%时，析出相中C、N 的占位数随温度的变化与图3 有着相同的趋势，但C 的占位数进一步升高，N 的占位数相应降低。

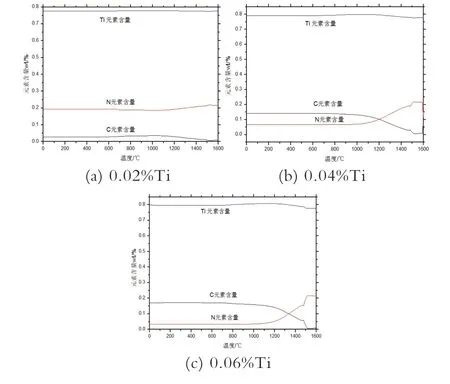
图3 Ti 含量不同析出相中元素组成

从抗拉强度分析，忽略马氏体强度的变化，Ti 的加入大幅度提高了铁素体的抗拉强度，如图4 所示。当Ti含量为0.02%时，双相钢的强度由无Ti 的596MPa 增加到662MPa。

图4 不同Ti 含量对双相钢强度的影响

4 含Ti 量为0.08%时不同中间温度对双相钢抗拉强度影响的Thermo-Cal 计算与分析

利用Thermo-Cal 软件分别计算出680℃～800℃不同中间温度下马氏体的体积分数和含C 量，对计算结果进行分析讨论并带入混合物定律计算双相钢强度。

由图5 可知，当中间温度由800℃降低到680℃时，随着铁素体转变量增加，奥氏体体积分数迅速降低，由44.8% 降低到4.2%。同时，随着温度降低，奥氏体体积分数曲线的斜率逐渐减少，说明奥氏体的分解速度逐渐减慢，这是由于随着奥氏体向铁素体转变的进行，铁素体体积分数不断增加，碳原子不断由铁素体向奥氏体扩散，造成奥氏体C 浓度的升高，增大了铁素体转变的形核功和驱动力，使得奥氏体向铁素体转变变得困难进而速度减慢。当温度降低到685℃左右，奥氏体体积分数曲线出现了一个拐点，之后分解速度明显加快。由图6 知，这也是由于奥氏体中碳含量在685℃出现极大值后逐渐减少，进而促进素体转变的缘故。以上分析说明，奥氏体的分解速率随着奥氏体体内碳浓度的降低而提高。

从抗拉强度分析，在Ti 含量一定并忽略铁素体强度随温度的变化，当中间温度由680℃上升到800℃，双相钢的强度逐渐升高，由559.6MPa 升高到798.3MPa。由公式（1）知，铁素体强度一定，双相钢强度主要由马氏体的强度和体积分数决定，又由公式（6）可知，马氏体强度与含碳量呈线性关系。通过T-C 软件计算出马氏体体积分数马氏体含碳量，进而算出马氏体强度和双相钢的强度，结果列于表2。

表2 不同淬火温度双相钢的性能参数

由上文分析可知，随着中间温度升高，奥氏体中含碳量降低，进而淬火后马氏体的碳含量减少，强度减弱。但随着中间温度的升高，奥氏体的体积分数增加，即淬火后马氏体的体积百分比增加。由双相钢总体上升的强度趋势可以知道，马氏体体积分数增加对双相钢的强度贡献大于马氏体自身强度减弱的影响。

5 结语

（1）本文研究了0.08C-1.5Mn-0.3Si(wt%)双相钢的抗拉强度，并完善了已有的强度预测模型，完善后的模型中双相钢强度影响因素除了马氏体体积分数，马氏体含C 量和铁素体晶粒尺寸，还考虑了第二相粒子的析出强化作用。

（2）Ti 的加入提高了双相钢的抗拉强度，在0.12%Ti 含量内，随着Ti 含量的增加双相钢的强度逐步增大。高温时析出相以TiN 为主，随着温度的降低，析出相逐渐转变为TiC。

（3）随着淬火温度的升高马氏体体积分数增加，马氏体含C 量下降，双相钢的强度增加。