模型思想在小学计算教学中的思考

江苏省南京市小营小学 王 欢

在我国新课标中明确指出，学生在数学学习过程中，如若想要理解、体会数学知识与现实生活中的联系，最重要也是最基本的途径是建立模型思想。在教学过程中，培养学生建立和求解数学模型的能力，可以有效激发学生对数学学习的兴趣以及应用数学解决相应问题的意识。因此，在小学生年龄阶段，培养学生形成良好的数学模型思想，并引导学生理解和掌握数学模型的建模过程，是当前小学数学教学的核心目标之一，同时也是培养学生形成良好的数学素养的重要方式。

在教学“两位数乘两位数的竖式计算”时，为了让学生理解计算算理，教师通过点子图，放手让学生自主探究，用学过的旧知识去学习新知识。

出示问题情境：每支钢笔14元，买12支钢笔，一共用多少元？

教师提问：同学们经过估算，得出了很多不同的结果，而这些结果中，我们怎么证明哪些结果与正确结果更加接近呢？

学生回答：可以通过计算14与12的乘积得出。

在此时，教师引导学生进行独立运算，并提示学生如果在计算的过程中遇到任何问题和困难，都可以利用点子图得到帮助，并将点子图展示给学生。同时，教师要给学生讲解点子图的用法，引导学生理解点子图。在点子图中，一行中共存在14个点子，那这些点子代表的是什么？这时教师可以给予提示，前面问题标明每支钢笔的售价是14元。接着教师可以继续发出提问：

教师提问：如果是三行的情况下，是哪一部分，该如何表示？

学生此时可能无法回答出来，这时候教师可以改变问题的方向。

教师提问：如何在点子图中圈出70？

学生回答：每一行是14，那么在点子图中圈中五行，就会得到70。

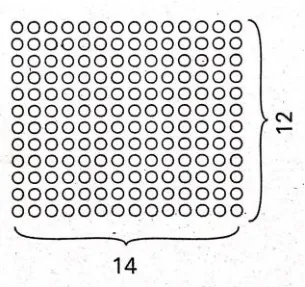
教师提问：是否需要逐个去查吗？那么，之前提到14与12的乘积是如何计算出来的？同学们可以利用点子图圈一圈，然后再算一下。

……

学生A：可以利用拆分的方式来分解这个点子图，在现在的点子图之中，每一行中有14个点，总共有12行，那么可以将行的数量分成10行和4行两部分，然后分别用10和4与12相乘，就会得出4与12乘积为48，而10与12乘积为120，将两个乘积结果相加后得出168。

教师提问：你是怎么想到会这样进行计算的？

学生A：因为直接计算14与12的乘积我不会，但如果分拆成为整数10的话，就非常容易计算了。

教师对另外一名同学提问：你觉得他的计算方法合理吗？这位学生就会发表自己对A同学所用的方法的观点。此时教师可以继续对班级内的学生进行提问。

教师提问：哪位同学还可以用其他的方式计算出14与12的乘积？

学生B：我也可以用拆分点子图的方式，但我却是将12拆成3份，每一份为3行，那么就可以先计算出其中的一部分，则为14×4=56，而总共为3份，就可以计算为14×4×3=56×3=168。

此时已经有两种点子图的拆分方式，但两种方式的计算结果却相同。教师可以继续提出问题：

教师提问：同学们认为以上两位同学所运用的拆分方法，谁的方法更加简单方便呢？

学生C：我认为学生A的拆分计算方式更加简单快捷，因为同样是拆分，但计算10与12的乘积和4与12的乘积更加简单。

此时，对于学生C观点认同的同学就会点头表示赞同。

教师评价：由此看来，在解决这个问题中，可以选择的方法很多，但以上同学可以自主想到利用拆分的方法来解题，真的非常聪明！如果在以后的学习中还会遇到这样的问题，同学们应该先仔细想想最好的拆分方式，而不要着急直接例如，刚才老师看到同学D的拆分方式是将12拆分，分别拆成10和2，请同学D说说自己的想法。

学生D：将点子图中竖着方向的数12分别拆成10和2，然后就可以在点子图中圈出两部分，其中第一部分的点数可以通过10与14的乘积计算得出140，而第二部分的点子数可以通过2与14的乘积计算出为28，将两个结果相加得出140+28=168。

教师提问：那么基于以上两种方式，你为何会想到将12分为10和2？

学生D：因为分出来整数10之后更加容易计算！

教师可以引导学生逐一发表自己在竖式方面的拆分方式。

……

通过点子图这样的计算模型，让学生在独立思考的基础上，全班交流汇报，展示算法的多样性，勾连图与算式为后续竖式计算的算理教学埋下伏笔，从而培养学生在计算过程中都是要先进行拆分，将点子图分为几部分后，再进行乘法的计算，进而就可以加深学生对“算理”的理解，巩固学生的竖式写法，也可以巩固学生的“算法”方面的知识。

以数学学习心理的角度进行分析，学生学习数学知识的过程属于不断探究、提高思维能力的过程。引导学生理解和表述“算理”，可以促使学生形成和提升进行“算法”计算的能力，同时学生学习数学更加是学生的数学思维活动的外显形式，也是培养学生形成良好的数学思维方式的有效平台。而如果从学生进行数学学习获得相应知识的过程的角度进行分析，通过引导学生探究、理解“算理”，可以培养学生与教师共同解决抽象的形式化数学问题，与此同时，可以实现在分析“为什么”的过程中，表述自身的形式化原理认识的模型化抽象过程。

模型思想是《标准》新增加的概念，需要教师在实际教学过程中加大落实的力度，在小学生的年龄阶段，学生对于模型思想还没有足够的理解和感悟，较比其他学科的理解和掌握程度还有一定的差距。因此，教师要在教学过程中引导学生将知识合理融合，从而培养学生形成良好的、理性的数学思维，进而提升学生在生活中解决实际问题的能力。