海洋环境下3C钢腐蚀速度多元非线性回归模型的建立及验证*

靳文博 李新战 肖荣鸽 赵 军 李 凯

(1.西安石油大学石油工程学院 陕西西安 710065; 2.陕西省油气田特种增产技术重点实验室 陕西西安 710065;3.中石油管道有限责任公司西气东输分公司甘陕管理处 陕西西安 710021)

钢材在海洋环境中的腐蚀比陆地上更为严重，腐蚀破坏不仅带来巨大的经济损失，甚至会引发安全事故[1-3]。海洋腐蚀可分为海洋大气区、浪花飞溅区、潮差区、海水全浸区和海底泥土区等5个不同特性的腐蚀环境，其中浪花飞溅区是钢结构腐蚀最为严重的区域[4-5]。3C钢作为一种碳素钢，以其在力学、物理、化学方面的优越性能而被广泛应用于海洋工程、化学工程、石油加工及炼化等相关领域[6]。关于3C钢在海洋环境中的腐蚀问题，学者们已开展了大量工作，其中腐蚀速度的研究一直是关注的热点。在研究钢材在海洋环境中的腐蚀速度时，可通过实验模拟的方法来进行，但该方法需要耗费一定的人力和财力，且不能完全代表实海腐蚀情况(海洋环境较为复杂)[7-8],因此建立海洋环境下钢材腐蚀速度的预测模型具有减少实验次数、方便获得腐蚀速率的优点。

海水是复杂的多种盐类的平衡溶液，其含有生物、悬浮泥砂、溶解的气体及污染物等，故金属的腐蚀速度与上述因素的综合作用有关[4]。影响腐蚀的主要海水环境因素包括温度、溶解氧含量、盐度、pH值、氧化还原电位及流速等，各环境因素之间存在着复杂的相互作用，给分析海水环境参数与腐蚀速度间的关系带来了困难，很难用一个具体的函数形式来表示[9-10]。为了预测不同海洋环境下钢材的腐蚀速度，不少学者采用神经网络模型来对其进行预测，取得了较好的效果[11-13]。但是，神经网络方法在预测的过程中不能得到模型的显式表达式，这给实际应用带来了一定不便。因此，基于腐蚀速度的影响因素，建立海水环境因素与腐蚀速率间的解析模型就显得很有必要，但目前针对此问题的专门研究很少。

多元非线性理论能较好地处理因变量与各自变量间的非线性关系，可根据数理统计的方法建立多个独立自变量与一个因变量之间的非线性函数关系。基于此，本文以3C钢在不同海水环境因素下的腐蚀行为为例，在分析各因素对3C钢腐蚀速度影响规律的基础上，基于多元非线性回归理论建立了计算3C钢腐蚀速度的多元非线性回归模型，并将计算结果与线性回归模型及实验结果进行了对比分析。本文研究结果对于海洋工程钢结构的设计和设备的安全运行具有一定的借鉴意义。

1 3C钢腐蚀速度多元非线性回归模型的建立

1.1 建模思路与方法

设因变量为Y，各自变量为xi，自变量共有n个。基于多元非线性回归理论，首先根据因变量Y与各自变量xi的关系，分别建立回归模型[14-15]，即

Y=fi(xi)

(1)

式(1)中:fi(xi)为某一自变量和因变量间的函数关系。

然后基于多元线性回归的思想，将式(1)中所建的模型整体作为多元线性回归的变量，令X1=f1(x1),X2=f2(x2),…，Xn=fn(xn)，设随机误差为ξ，则因变量Y与各自变量(X1,X2,…，Xn)的线性回归模型可表示为

Y=k0+k1X1+k2X2+k3X3…+knXn+ξ

(2)

式(2)中:k0、k1、…、kn为回归系数。

在实际中若获得N组自变量和因变量的观测数据，则可在分析各自变量和因变量间关系的基础上，根据式(1)和式(2)建立因变量和自变量的多元非线性回归模型。

文献[16-17]也给出了建立自变量与因变量间非线性数学模型的步骤，具体为：①先单独考虑每个自变量与因变量之间的关系，得出各自变量和因变量的数学模型；②将这些数学模型逐一叠加，若叠加后的模型不满足要求，则考虑各自变量之间的相互作用，最终可得到相应的多元非线性数学模型。该建模思路所得模型适用于普遍情况，且与实际情况的吻合程度高，模型的具体数学表达式为

(3)

式(3)中:Y为因变量；ai、bm、k为回归系数；xi、xj为自变量。

本文基于上述建模思路和方法，建立了海洋环境下3C钢腐蚀速度多元非线性回归模型。

1.2 模型建立

影响腐蚀速度的海水环境因素较多，且各因素间的关系复杂。刘学庆 等[18]选取了海水温度、溶解氧含量、盐度、pH值以及氧化还原电位等5个因素，研究了不同海水环境因素对3C钢腐蚀速度的影响，并利用灰色关联法探讨了环境参数对碳钢腐蚀速度的影响程度，认为影响腐蚀速率的海水因素从大到小的顺序为：氧化还原电位、温度、溶解氧、pH值以及盐度。文献[4]的分析结果也表明，溶解氧含量、氧化还原电位及温度等3个参数对腐蚀速度的影响较大，而盐度和pH值对腐蚀速度的影响较小。同时，作者也指出在建立腐蚀速度预测模型的过程中，如果预测模型的精度要求不高，则可以只考虑温度、溶解氧及氧化还原电位等3个环境参数；如果要建立预测精度高的模型，则必须同时考虑上述5个环境参数。

为了建立腐蚀速度的多元非线性回归模型，需要分析海水环境参数与钢材腐蚀速度间的关系。一般而言，温度升高，化学反应的速度增加，腐蚀速度增快，但当温度升高到一定程度后溶解氧含量会降低，进而阻碍钢材的腐蚀[18]；盐度的升高造成电导率的增加，加快钢材的腐蚀，但当含盐量到达一定值时腐蚀速度反而会降低，因此温度和盐度改变时腐蚀速度的变化应存在一个极大值。一般地，溶解氧含量越高，腐蚀速度越快，其腐蚀速度与溶解氧含量基本呈线性关系；pH值越高，腐蚀速度越低，其腐蚀速度与pH值的关系也基本为线性；对于氧化还原电位而言，其与腐蚀速度基本呈线性关系，氧化还原电位越高，则钢材的腐蚀速度越快[4]。

本文以温度(x1)、溶解氧含量(x2)、盐度(x3)、pH值(x4)及氧化还原电位(x5)为自变量，腐蚀速度(Y)为因变量来建立多元非线性回归模型。基于上述分析，假定腐蚀速度与温度和盐度间的关系式可用三次多项式来表达，且在自变量相互作用项中考虑了主要自变量间的相互作用，它们之间的关系式依据文献[3]的实验数据(表1)，采用多元逐步回归分析法进行计算后得到。进而可建立多元非线性回归模型，即

Y=k0+k1f1(x1)+k2f2(x2)+k3f3(x3)+

(4)

其中

(5)

式(5)中:a1、a2、…、a9,b1、b2、…、b5均为回归系数；x1、x2、…、x5为自变量。

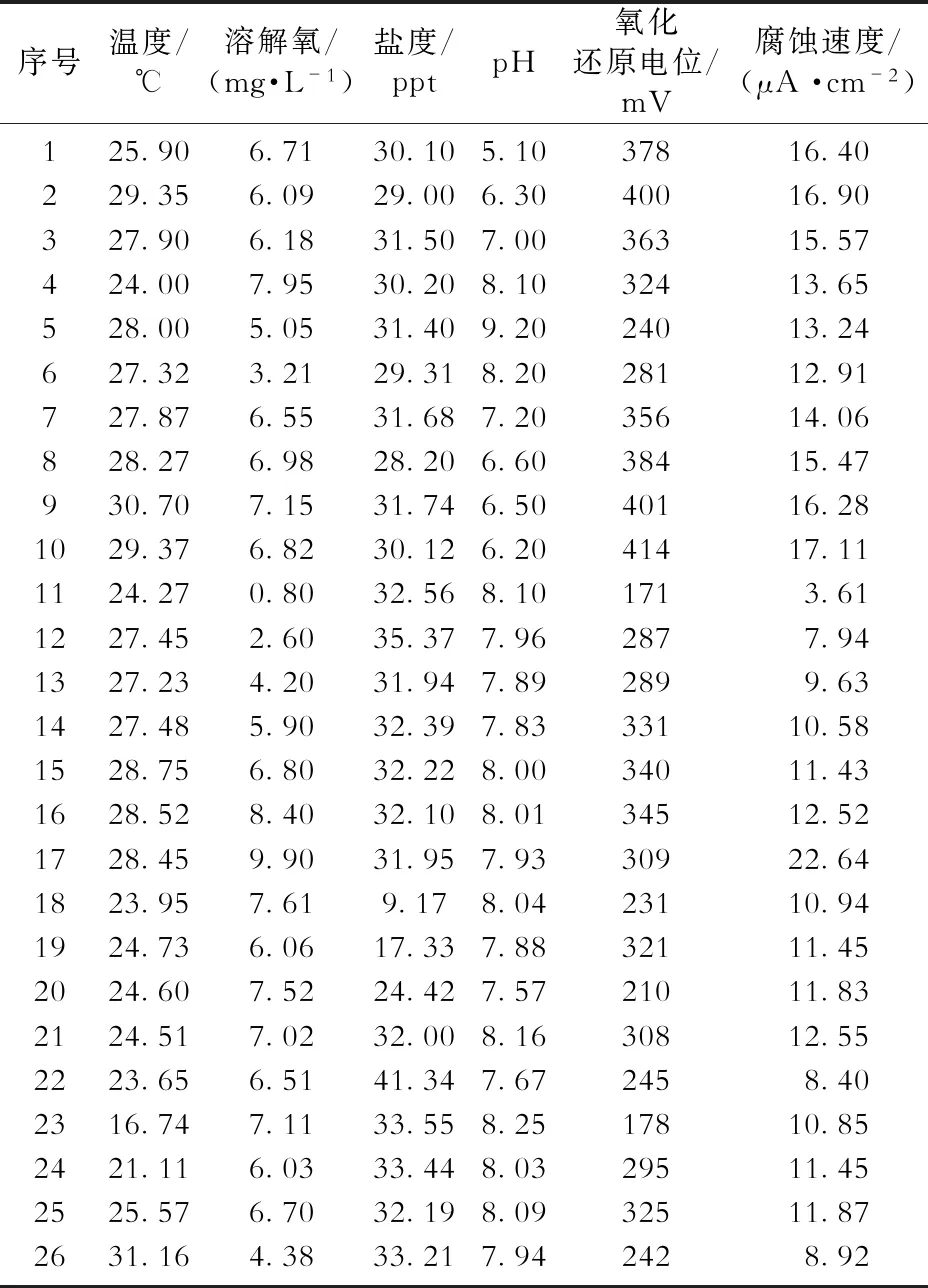
表1 3C钢在不同海水环境参数下的腐蚀速度实验数据Table 1 Experimental data of corrosion rate of 3C steel under different seawater environmental parameters

上述模型(即非线性模型一)考虑了自变量间的相互作用影响。若不考虑自变量间的相互作用，即式(4)中右边最后一项为0，则可得到模型的另外一种表达式(即非线性模型二)为

Y=k0+k1f1(x1)+k2f2(x2)+k3f3(x3)+

k4f4(x4)+k5f5(x5)

(6)

式(6)中，f1(x1)、f2(x2)、f3(x3)、f4(x4)及f5(x5)的表达式与式(5)相同。

2 模型验证及计算结果分析

文献[3]报道了不同海水环境因素下3C钢的腐蚀速度实验测试结果，所采用的实验仪器和方法具体为：实验所用海水为青岛海域的海水，采用YSI 6600多参数水质监测仪测试海水的环境参数，在控制1种环境因素的同时，记录其他环境因素的变化情况；采用电化学测试的方法来获得3C钢的腐蚀速度，测试仪器为Solartron公司SI 1287 electrochemical interface，采用三电极体系，即钢材电极作为工作电极，铂电极作为辅助电极，饱和甘汞电极作为参比电极。本文基于上述实验数据(表1)[3]，对所建模型的合理性进行分析。在表1中，实验数据共计26组，影响3C钢腐蚀速度的因素有5个，分别为：x1—温度；x2—溶解氧；x3—盐度；x4—pH值；x5—氧化还原电位。

基于表1的实验数据，利用MATLAB中的非线性函数nlinfit，对模型中的相关参数进行拟合，可以得到非线性模型一和非线性模型二，分别如式(7)、(8)所示。

y=-16.688 3-0.0325 2x13+2.345 44x12-

37.817 33x1-4.335 19x2-0.000 96x33+

0.075 39x32-3.039 78x3+49.247 6x4+

0.517 61x5+0.000 1x1x3-1.650 28x1x4-

0.014 6x1x5+0.189 5x2x3-0.021 62x4x5

(7)

y=112.558 52-0.008 21x13+0.601 28x12-

14.148 2x1+1.181 72x2-0.000 33x33+

0.013 05x32+0.011 75x3-0.786 41x4+

0.006 24x5

(8)

为了进一步对比非线性模型和线性模型计算结果的差异，本文还给出了多元线性模型的回归结果，即

y= 0.249 06+0.237 26x1+1.119 61x2-

0.004 71x3-0.626 49x4+0.013 43x5

(9)

采用多元非线性模型一、多元非线性模型二及多元线性模型，可计算得到不同海水环境因素下3C钢的腐蚀速度，将三者的计算结果与实验值进行了对比，得到了模型的计算值和实验值的相对误差(取误差的绝对值进行计算)，具体结果见表2。

从表2可以看出，非线性模型一的最大相对误差为24.181%，最小相对误差为0.296%，其相对误差在20%内的数据样本共有25组，相对误差在10%以内的数据样本共有16组，相对误差在5%以内的数据样本共有11组；非线性模型二的最大相对误差为30.671%，最小相对误差为0.548%，其相对误差在20%内的数据样本共有20组，相对误差在10%以内的数据样本共有14组，相对误差在5%以内的数据样本共有10组；线性模型的最大相对误差为36.190%，最小相对误差为1.228%，其相对误差在20%内的数据样本共有19组，相对误差在10%以内的数据样本共有16组，其相对误差在5%以内的数据样本仅为7组。

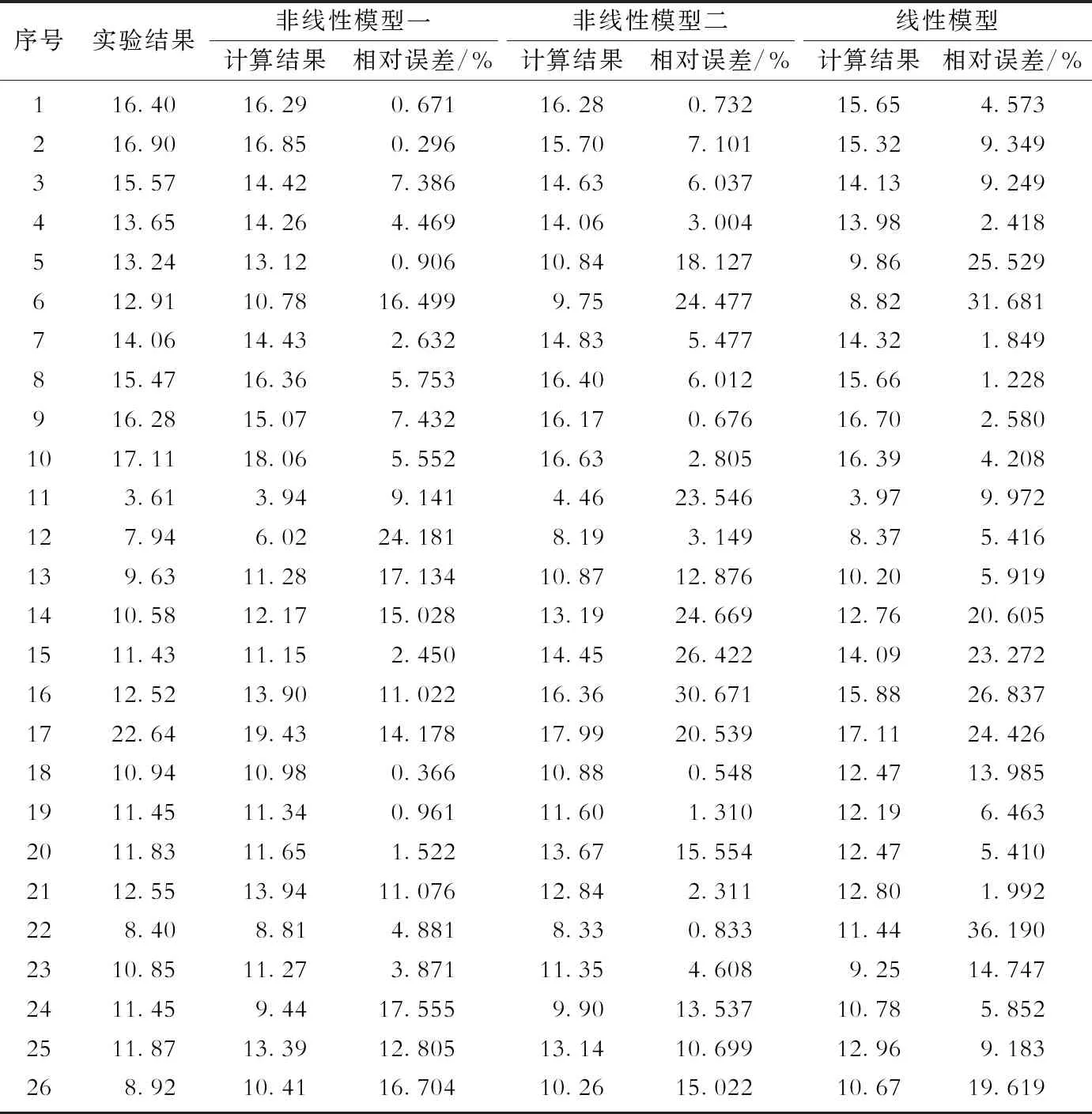
表2 不同模型计算结果和实验结果的对比Table 2 Comparison between calculation results of different models and experimental results

根据表2的数据，计算各模型的平均相对误差和均方误差。其中，非线性模型一的平均相对误差为8.249%，均方误差为1.607；非线性模型二的平均相对误差为10.798%，均方误差为3.236；线性模型的平均相对误差为12.406%，均方误差为4.169。

综合分析上述计算结果可知，非线性模型一的精度较高，非线性模型二的精度次之，而线性模型的精度较差。因此，考虑各自变量的相互作用下所得的非线性模型精度高于未考虑各自变量相互作用时的非线性模型精度。

图1给出了上述3种模型的误差对比图，可见非线性模型一的相对误差基本在20%以内，其相对误差分布较为集中，误差值离X轴较近，而非线性模型二和线性模型的误差分布则相对分散，因此非线性模型一的精度相对较高。

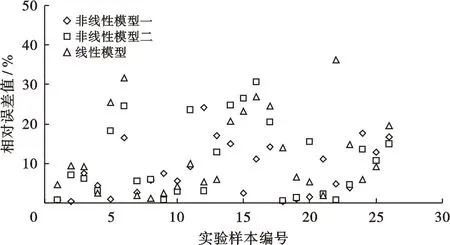
图1 各模型的误差对比Fig.1 The error comparison of each model

3 结论

基于多元非线性回归建模的相关理论，通过分析海水环境参数与3C钢腐蚀速度之间的关系，在考虑各自变量相互作用和未考虑各自变量相互作用情况下，建立了3C钢腐蚀速度的多元非线性回归模型，并将其计算结果与多元线性回归模型计算结果和实验结果进行了对比。结果表明：多元非线性模型的计算精度高于线性模型的计算精度；考虑各自变量相互作用时的多元非线性模型的计算精度高于未考虑各自变量相互作用时的多元非线性模型的计算精度；且考虑各自变量相互作用的多元非线性回归模型计算结果与实验结果吻合程度较好；此外，本文将温度和腐蚀速度、盐度和腐蚀速度之间的关系用三次多项式来表达，从模型的计算精度可知此种做法具有一定的准确性，表明该建模方法可为海洋环境下3C钢腐蚀速度的预测提供有益借鉴。