莺琼盆地高温高压钻井工程风险定量评价方法*
黄 熠 杨 进 胜亚楠 管志川 罗 鸣
(1.中国石油大学(北京)石油工程教育部重点实验室 北京 102249; 2.中海石油(中国)有限公司湛江分公司 广东湛江 524057;3.中国石油大学(华东)石油工程学院 山东青岛 266580)
我国南海地区超过75%的区域发育高温超压地层,天然气蕴藏量巨大,具有广阔的勘探开发前景。该区域钻完井施工的主要难点为高温、高压、安全密度窗口窄、地层压力信息不确定性强,施工过程中频繁出现涌、漏、塌、卡等井下复杂情况,严重制约了勘探开发进程。海上高温高压井钻井是高风险、高投入的系统性工程[1-3],由于复杂地质环境下地层压力准确预测难度大,预测结果存在不确定性,当钻井设计不得不依靠这些不充分、不精确的数据时,就会引发钻井风险[4-6]。钻井工程风险评价是保证钻井安全有效进行的一个重要手段,国内外学者先后建立了层次分析法、故障树法、人工神经网络法等[7-11]。通过上述文献调研发现,现有的钻井风险评价方法大多是将经典风险分析方法移植到钻井工程领域,并且得到的结果往往都是定性和半定量的,现场使用效果反馈传统的钻井风险评价方法无法满足海上高温高压复杂地质环境下高风险钻井施工作业的安全要求,因此有必要建立一套钻井工程风险定量评价方法。本文针对南海莺琼盆地高温高压钻井施工过程中工程风险事件发生概率较高、处理难度大的问题,在地层压力和钻井液当量循环密度(ECD)不确定性分析研究的基础上,建立了一套钻井工程风险定量评价方法,可实现钻井风险评估与预测,并采取相应的措施降低和控制工程风险,从而保障南海莺琼盆地钻井作业高效、安全。
1 莺琼盆地高温高压井钻井存在问题
莺琼盆地高温高压地层发育,储层埋深3 500~4 000 m,区域地层温度超过200 ℃,地层孔隙压力系数超过2.30,该区域高温高压条件处于世界上最严酷的范围,几乎已达到目前行业极限。该区域具有温度高、压力高、压力台阶多、安全密度窗口窄等地质特性,对高温高压钻井工程设计和作业提出了巨大的挑战[12-13]。莺琼盆地区域高压形成机制多样,压力预测存在较大不确定性。从已作业井来看,工程风险问题突出的原因之一是复杂地质环境下地层压力预测结果的不确定性较大,对于地层压力认识不清,导致井身结构针对性和钻井液密度设计精确性差,最终使得钻井施工过程中工程风险事件发生概率较高,处理难度大,严重制约了高效、安全钻井作业。例如,南海莺琼盆地某气田是发育在底辟塌陷背景上的中层岩性圈闭,钻遇地层主要为砂泥岩地层,尤其是泥岩地层发育,地层中存在多套大段泥岩层。根据该气田已钻井情况来看,出现的主要复杂问题是上部地层在起下钻过程中阻卡现象较为严重,需要进行划眼、倒划眼作业,在钻井中还多次出现憋扭矩问题,严重影响作业进度;而下部地层复杂情况主要与异常高压有关,在高压层钻进时需要用很高的钻井液密度来平衡地层压力,压力窗口窄,高密度钻井液导致漏失事故频发[14-15]。
2 钻井工程风险定量评价方法
2.1 地层压力不确定性分析
地层孔隙压力、地层破裂压力及坍塌压力剖面是井身结构设计的重要依据。高温高压复杂地质环境下地层压力预测难度大,预测结果存在不确定性,综合分析认为主要原因有地质环境本身的复杂性使得地层压力成因多源化、测井与地震等解释资料存在误差以及压力预测模型的区域适用性等问题。柯珂 等[16-17]在综合考虑了伊顿指数、岩石力学参数和地应力的空间区域分布特征的基础上,基于蒙特卡洛模拟和概率统计分析原理构建了地层压力不确定性分析方法,最终得到的地层压力不再是单一定值,而是具有概率分布特征的区间。笔者在上述研究的基础上提出地层压力不确定性分析流程,如图1所示。
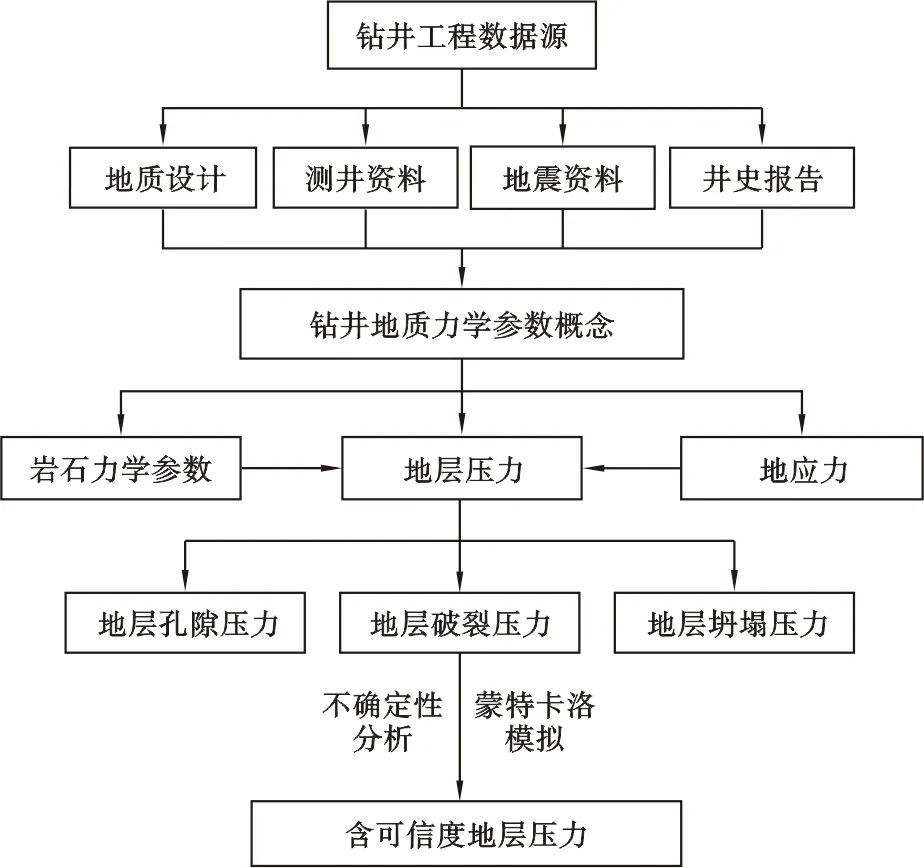
图1 含可信度地层压力求取流程Fig.1 Calculation flow chart of formation pressure with credibility
2.2 ECD不确定性分析
ECD是维持井筒压力平衡的重要参数,正常钻进过程中ECD要时刻保持在安全钻井液密度范围内,这样才能保证钻井安全。ECD的计算公式为[4]
(1)
式(1)中:Q为钻井液循环当量密度,g/cm3;Qs为静态钻井液密度(ESD),g/cm3;pc为井深H处环空压力损耗,MPa。
ESD和环空压耗的计算模型可参考文献[18-22],本文不再累述。由于ECD计算参数的模糊性和计算精度等问题,导致ECD存在一定的不确定性,这也是引发钻井风险的根本原因之一。针对这一问题,管志川 等[23]基于不确定度分析理论建立了ECD概率分布的求解方法,即定义x1、x2、…、xn等n个直接测量参数为ECD计算模型参数,则间接测量参数Y(代表ECD)与{x1,x2,…,xn}之间的函数关系为Y=F(x1,x2,…,xn)。具体求解步骤如下:
1) 确定直接测量参数概率分布函数f1(x)、f2(x)、…、fn(x);
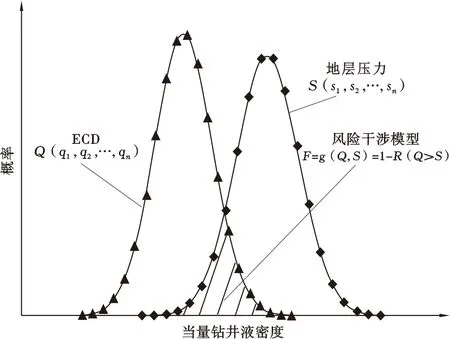
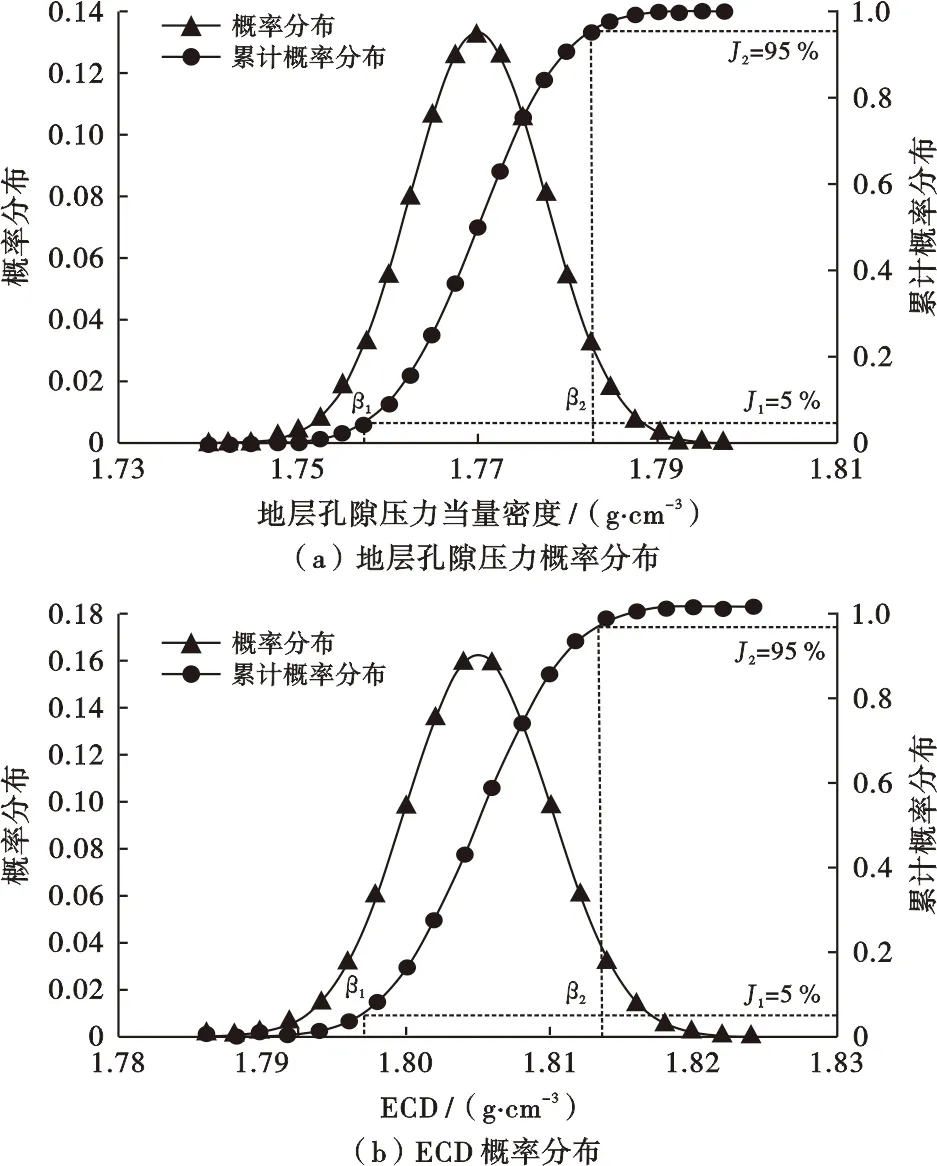
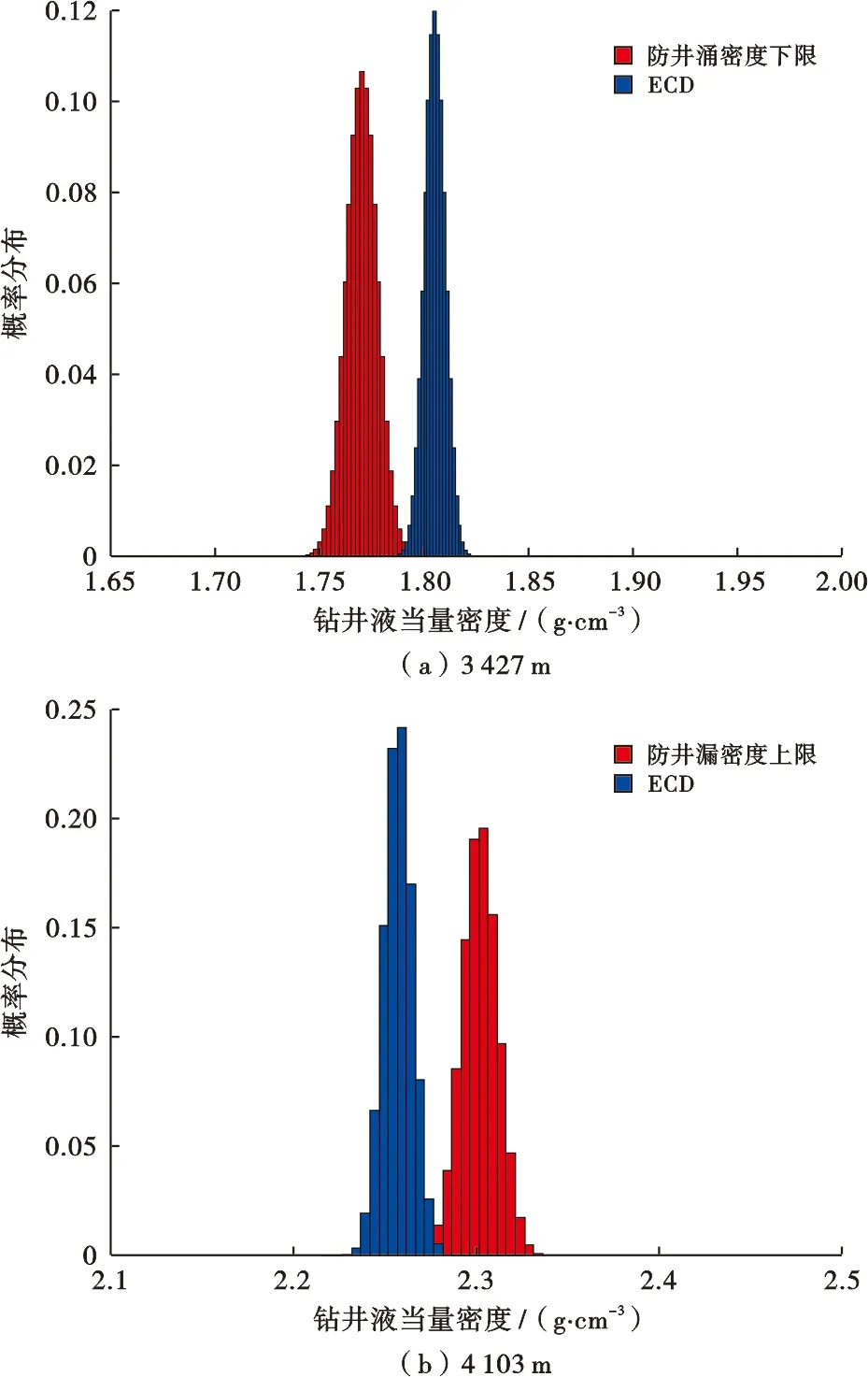
2) 确定模拟次数N,产生符合概率分布特性的N个直接参数X1、X2、…、XN的随机数样本,其中,Xi=[x1i,x2i,…,xni] (1 3) 将每个随机数样本Xi=[x1i,x2i,…,xni] (1 4) 统计分析Y=[Y1,Y2,…,YN],确定ECD的概率分布f(y)。 综合考虑钻井工程风险的致险机理[24],维持井筒液柱压力与地层压力相互平衡是保持钻井安全的前提。结合可靠性理论,定义井筒内液柱压力(即井底ECD)为广义致险因子,定义地层压力(包括孔隙、坍塌和破裂压力)为安全因子,最后建立井下复杂与事故的风险函数,得到功能函数,最终构建了风险概率计算模型。以井涌风险为例,具体阐述钻井工程设计风险定量评价方法。地层压力-循环当量钻井液密度分布干涉模型原理如图2所示,从图2得到,当2个概率(Q与地层孔隙压力值S)分布发生干涉时,就说明有钻井风险发生,其中阴影部分表示风险发生概率,计算公式为 图2 地层压力-循环当量钻井液密度分布干涉模型原理Fig.2 The interference model principle between distribution pore pressure and ECD F=1-R (2) 式(2)中:F为钻井工程风险发生概率;R为钻井液功能的可靠度。 Q和S都包含随机变量参数,即 (3) 式(3)中:xQ1,xQ2,…,xQn为ECD有关的变量(如井径、排量和钻井液密度等);xS1,xS2,…,xSn为地层孔隙压力的变量(如伊顿指数、正常压实趋势线、地应力等)。钻井液功能可靠度和失效概率可以表示为 (Z≥0) (4) (Z<0) (5) 式(4)、(5)中:f(Z)为干涉函数,Z=Q-S;fQ(Z+S)=fQ(Q),表示ECD随机变量Q的函数;fS(S)表示地层压力随机变量S的函数。 由上述2个公式可知,只要确立了ECD和地层压力的概率分布,即可以得到钻井风险发生的概率。假设ECD随机变量Q与地层压力S随机变量均满足正态分布[25-26],即 (-∞<σQ<+∞) (6) (-∞<σS<+∞) (7) 式(6)、(7)中:μQ、μS、σQ、σS分别为二者的均值和标准差;fQ(Q)表示ECD随机变量Q的函数;fS(S)表示地层压力随机变量S的函数。 在Q与S均为正态分布时,Z=Q-S也为正态分布,其计算公式为 (-∞<σZ<+∞) (8) 当Q>S或Q-S>0时,钻井安全,故可靠度R表达式为 (9) 钻井工程风险发生的概率与可靠度是互逆概率,即风险发生概率F计算公式为 (10) 莺琼盆地先期探井钻井实践表明,地层压力预测值误差较大,使得井身结构设计无法满足安全钻井需求,钻井过程中频繁发生井漏和溢流风险,严重制约了该地区的高效钻井开发。利用本文算法对莺琼盆地内一口高温高压探井LD10-1-X进行钻井工程风险评价,以期达到降低风险的目标。选取该区块内与该井具有相似构造的4口已钻井XX-1、XX-2、XX-3和XX-4为相邻井,收集这4口井的测井资料,得到地质力学参数的测井解释结果;根据地层压力不确定性分析方法,得到井深3 427 m处的孔隙压力概率分布;然后,根据ECD不确定性分析方法,得到钻进到井深3 427 m处的ECD概率分布;通过概率分布函数估计均满足正态分布,分别得到二者的概率分布,结果如图3所示。同理,可以得到钻进至4 103 m处地层破裂压力以及ECD概率分布,结果如图4所示。 图3 钻进至3 427 m处地层孔隙压力和ECD概率分布Fig.3 Probability distribution of formation pore pressure and ECD while drilling into 3 427 m 在上述分析结果的基础上,根据钻井工程风险定量评价方法对钻进到井深3 427 m处和钻进至4 103 m处可能发生的风险进行评价,结果如图5所示。从图5a可以看出:2种概率分布发生干涉,可以定性地说明可能发生井涌风险;根据钻井风险概率定量计算模型,编程计算求得当钻进到该井深位置上时井涌风险发生的概率为0.45。从图5b可以看出:2种概率分布发生干涉,可以定性地说明可能发生井漏风险;根据钻井风险概率定量计算模型,编程计算求得当钻进到该井深位置上时井漏风险发生的概率为0.4。根据LD10-1-X井实际作业时的钻井日报可知:在钻进至井深3 427 m处发生了井涌,在钻井至井深4 103 m处发生了井漏,评价结果与实际相符,从而验证了本文算法的科学性和有效性。 图5 LD10-1-X井3 427 m 和4 103 m处地层压力和ECD概率分布Fig.5 Probability profile of formation pressure and ECD at 3 427 m and 4 103 m of Well LD10-1-X 针对南海莺琼盆地高温高压钻井施工过程中工程风险事件发生概率较高、处理难度大的问题,首先对地层压力的不确定性进行了分析,并基于不确定度分析理论对井底钻井液当量循环密度不确定性进行概率分布分析,在此基础上基于广义应力与强度干涉的可靠度理论建立了钻井工程风险概率定量计算模型,并进行了实例分析,结果表明基于本文建立的钻井工程风险概率定量计算模型计算得到的风险评价结果与实际风险发生相吻合,可对钻井风险进行预测,从而保障南海莺琼盆地钻井作业高效、安全。2.3 钻井工程风险概率定量计算模型
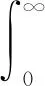
3 实例分析
4 结论

