BA模型下动态银行网络熵与系统风险研究

张泰源

（湖北大学楚才学院 湖北 武汉 430062）

一、引言

银行市场中存在金融联系，这使得银行间市场可以表现为一个网络。伴随金融自由化、复杂化趋势的发展，金融危机迅速蔓延的可能性快速增加［1］。许多文献开始利用银行网络研究系统性风险。其中由PaulErdos等人提出的随机网络模型以简单和随机连接著称，却无法替代真实复杂的网络；Wattz等人发现一些具有较短的平均距离和较大集聚系数的网络可以反映很多现实中的现象，被称为小世界网络；Albert等人通过研究网络幂律型度分布，提出一种名为无标度网络，这类网络在小世界特征的基础上又具有许多新的性质，更符合动态银行网络特征［2］。近年来统计物理学领域在复杂网络的特征研究方面有显著的进展，研究发现熵可度量网络的拓扑特性。然而采用熵来进行银行间网络与系统风险的研究有限。其中李［3］将网络熵的度量应用于全球金融网络数据库以研究高度互联的全球银行网络。一些研究表明熵的概念可用来建立系统风险预警指标［4］。上述分析可看出熵度量很少被用来分析银行网络和系统风险。单一研究仅采用网络熵来衡量高度互联的全球银行网络的多样性。文章旨在从系统风险的角度研究动态银行系统的网络熵特征，从无标度网络的角度出发，探究了网络熵与系统风险的关系，为现有文献增加内容。

二、基于无标度网络的研究

针对利用无标度网络探究银行网络熵与系统风险关系的问题，文章依次从动态银行系统的建模、无标度网络算法的应用和网络熵的求解展开，根据数学理论模拟分析网络熵与系统风险的关系。

（一）动态银行系统的建模

文章基于Lux［5］的研究对动态银行系统进行建模。假设银行k的资产包括投资、同业贷款和流动资产。负债包括存款、同业借款和资产净值。在期初假设银行间市场尚不存在，规定，，，。其中和分别表示初始阶段银行的总资产和总负债。在模拟中采用以下算法确定银行系统如何从一种状态演变到另一种状态。第一

阶段更新流动资产和资产净值如下：

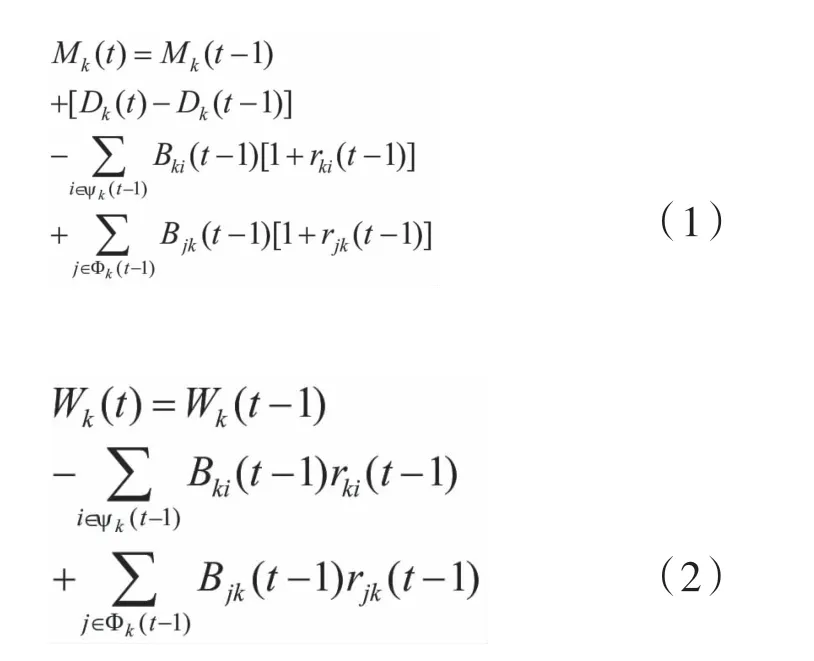
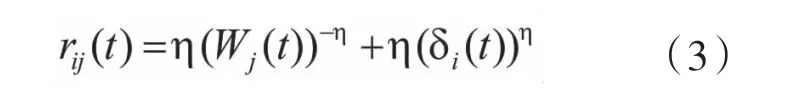
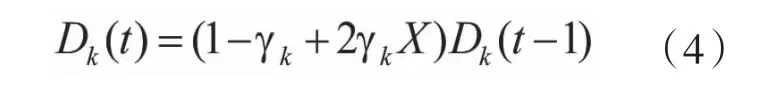
第三阶段是信用贷款。假设银行k的第t期有一个流动资产阈值，此保证了正常业务运营的持续，且。对于净资产为正的银行，若其流动资产低于阈值则为潜在的借款人，否则为潜在的贷款人。流动性需求或供给可用来表示。每一期假设存在潜在网络，潜在借款人与多个银行联系尽可能满足其流动性需求，潜在贷款人按借款人净资产由高到低的顺序给予资金。假设在借款人的流动性需求得到满足前，资金不会从贷款人转移到借款人手中。文章规定银行数量恒定不变，并提出违约银行总被一个新隐含取代的机制。

（二）无标度网络算法

无标度网络中大部分节点度很小，而很少一部分节点却拥有大量的连接，表现在度分布上便是幂律的形式，这与现实世界中的银行网络结构类似。无标度网络模型有多种，常用的有Price模型和BA模型。Price模型的提出解释了许多网络中存在的幂律度分布，却很少被使用在社会科学领域。现实中的网络规模随着时间不断增大，而随机网络和小世界网络中均假设网络开始时节点数固定，然后随机连接（ER）、重连（WS）或加边（NW）。其次现实网络中新的节点更倾向于和度很大的节点相连接，这种现象也称作“马太效应”。BA模型考虑到以上两点特性：现实网络的增长特性和优先连接特性。为了更加符合真实情况建模，文章基于BA模型使用无标度网络算法，构造如下：

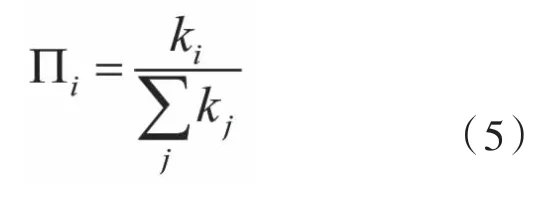
图1 网络演化示例（）

文章生成了100个节点的小世界网络。具体构建参数如表1所示。

表1 小世界网络中的参数设置

网络的标度最终将保持不变，即网络中的度分布将不会随着网络当中节点数N而改变。

（三）网络熵

结合动态银行系统模型和无标度网络算法，可将邻接矩阵转换成随机矩阵。其中表示银行j在t时刻对银行i的负债。

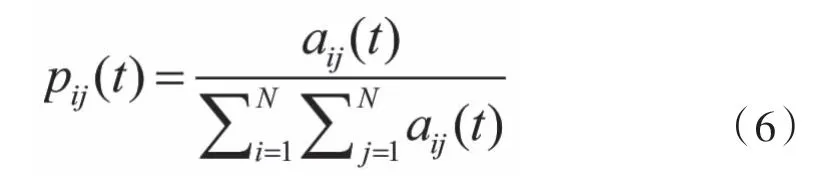
接着运用如下公式求出网络熵：

2实验结果与分析

Demetrius等人研究了具有不同拓扑熵的三类网络的网络解体过程，发现网络熵与鲁棒性呈正相关，其中网络分析包括无标度网络、随机网络和规则网络。文章从系统风险的角度研究网络熵是否可以作为衡量银行系统稳健性的一个尺度。通过数值模拟重复400次平均出随机效应，采用违约数和银行总数的比值BN作为度量系统风险的影响。运用Pearson的相关方法研究网络熵S2与系统风险效应之间的相关性。根据SPSS求得的相关性系数为0.837，如表2所示：

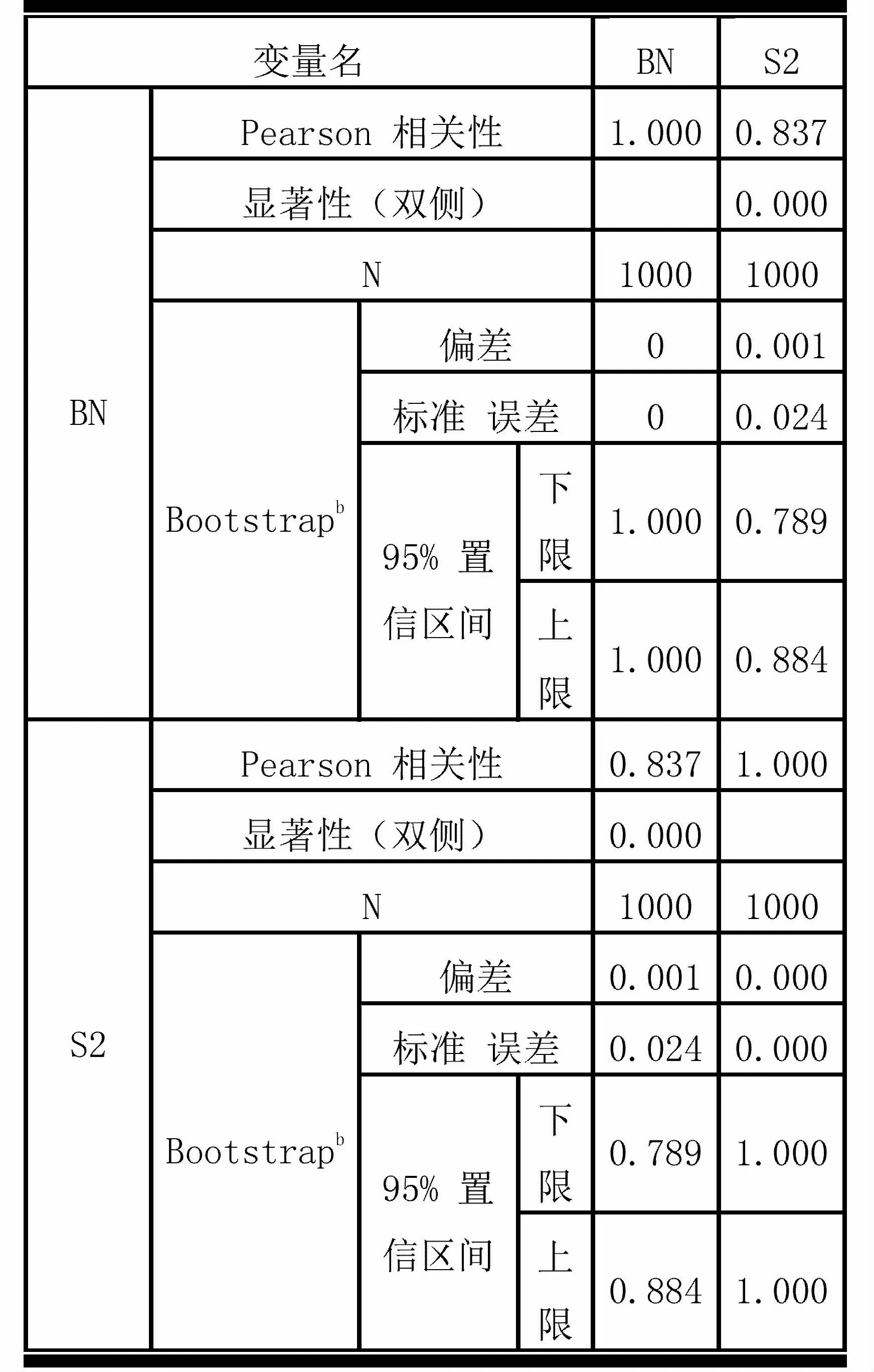
表2 Pearson相关性分析

从表2可看出网络熵与系统风险影响正相关。文章采用BA模型结合动态银行网络模型进行网络熵和系统性风险的求解。图2显示了网络熵与系统风险在不同时期下的结果，两者的变化趋势相似，都在快速增加后呈现下降趋势，并且随着时间的变化趋于稳定。表明网络熵可作为银行系统稳健性的尺度。

图2 网络熵与系统风险

三、总结

文章首先构建人工银行系统，然后研究了动态银行网络熵，分析了无标度网络。仿真分析表明网络熵的变化趋势和系统风险类似，两者正相关。

同时，文章的方法也存在一定局限性，文章的网络为无权网络，无法更加真实地反映节点之间相互联系的强弱。例如银行之间的业务联系程度会有所不同，节点之间的权重不能都通过1来代替。通过实际网络研究者发现，加权网络下节点的度、权重以及边全都复合幂律分布的特征［10］。因此未来的工作将致力于优化算法，将原有的无权网络按照银行业务联系的强弱修改为加权网络，构建更加符合实际情况的模型。