基于土料参数时变特性的土石坝渗透破坏概率动态分析方法

欧 斌,傅蜀燕,林志祥,高胜松

(1.云南农业大学水利学院,云南 昆明 650201;2. 河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098;3.云南农业大学机电工程学院,云南 昆明 650201)

我国是世界上拥有水库大坝最多的国家,土石坝因其施工便捷、便于取材、对地质要求低等优点,占比超过95%[1],土石坝结构安全是水利工程安全保障的重中之重。水利部先后3次对我国溃坝失事的统计表明,中国已溃决土石坝中由于渗透破坏造成的失事事故约为40%[2],土石坝渗透破坏发生包含随机、时变等系统性特征,国内外学者对此开展了一系列研究工作。王林等[3]根据地勘资料,将不同土层渗透系数视作服从一定概率分布的随机变量,计算其对渗流场总水头势、流速及渗透体积力的变异性影响规律;李益等[4]借鉴吴增光等[5]关于渗透系数与时间存在反正切函数关系的结论,分析了土石坝渗透破坏的时变效应;姜树海等[6]采用Bayes方法利用一切可以利用的先验信息,并通过不断的实时采样信息,修正和改进原有的概率分布规律假设,分析了随机变量的时变特性对渗流风险率的影响。上述研究都只针对其中的某一特征展开研究,未能反映土石坝渗透破坏随机、动态的演变过程。

鉴于土石坝渗透破坏发生的随机和时变综合特性,本文从土体材料参数随机与演变的规律出发,一方面将影响土石坝渗透稳定的核心土力学指标黏聚力和内摩擦角视为随机变量,基于原状土土工试验,充分考虑其变异性及相关性,并辅以干湿循环试验模拟其时变规律;另一方面,基于土石坝测压管实测长序列数据,反演土石坝渗透系数时变规律,构建动态土石坝渗透稳定判定功能函数,从而求解土石坝时变渗透破坏概率。

1 土石坝渗透破坏概率计算基本原理

渗透破坏发生的根本原因是出逸比降超出临界渗透比降,其中出逸比降可通过渗流有限元分析确定,土石坝渗透稳定的功能函数可表示为

Z=Jl-Jc

(1)

式中:Jl为土体的临界渗透比降;Jc为出逸比降。

土体发生流土破坏时临界渗透比降可表示为[5]

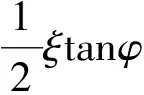
有n个影响渗流稳定安全性的随机变量(x1,x2,…,xn)时,土石坝渗流的状态方程可表示为

Z=g(x1,x2,…,xn)

(3)

式中:x1、x2、…、xn为具备变异性且服从一定分布的随机参数。随机抽取N次满足精度后,在N次抽样中出现Z=g(X)<0的次数为M(其中X=(x1,x2,…,xn)),则土石坝渗透破坏概率为

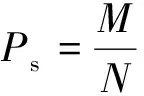
(4)

2 土石坝时变渗透破坏分析的实现方法

2.1 基本思路

Monte Carlo法是抽样计算中应用最成熟和最广泛的方法,便于与有限元方法结合使用,且只要模拟足够多的抽样次数,就能得到准确的失效概率,但缺点是计算量过于庞大,拉丁超立方抽样(Latin hypercube sampling,LHS)方法对其进行了改进,抽样生成的随机数分布更加均匀,避免了重复抽样,从而提高了收敛性能[7]。

LHS方法虽减少了随机抽样工作量,但计算工作量依旧较大,且运算过程中容易出错致使全部计算重来,径向基函数神经网络(radical basis function,RBF)技术具有很强的非线性映射能力、强大的自学习能力以及高度的容错性,便于找出自变量与效应量之间的映射关系,从而比较理想地逼近结构的极限状态方程[8]。将两种方法相结合更易于解决结构的极限状态方程Z=g(X)=0等复杂问题,从而大大减少计算成本,降低出错概率,优化工作效率。

2.2 实现步骤

融合RBF神经网络与LHS方法,利用有限元求解土石坝时变渗透破坏概率的操作步骤如下。

步骤1:将渗流有限元计算水位值和测压管实际水位值相比较,使误差最小从而得到最优的反演渗透系数。误差函数为

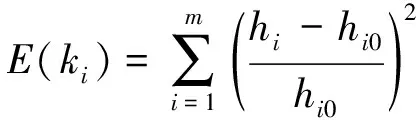
(5)

式中:ki为不同土层渗透系数;hi为计算水头;hi0为测压管水头;m为测压管根数。

考虑约束条件,渗透系数的优化模型为

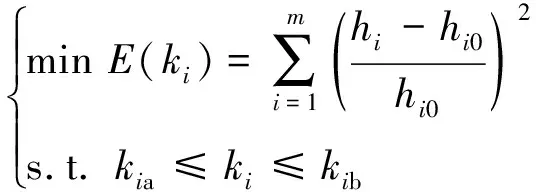
(6)

式中:kia、kib分别对应不同土层渗透系数ki的最小和最大值。通过式(6)反演不同年度的平均渗透系数,计算得出不同年度坝脚和坝后覆盖层的出逸比降。

步骤2:取坝脚、坝后覆盖层原状土，参照筑坝初期试验值，结合干湿循环试验获取不同干湿循环次数下黏聚力与内摩擦角试验值与变异系数,并拟合其规律。

步骤3:计算不同年度土体参数随机变量xi(组数为S)在坝脚和坝后覆盖层的出逸比降q(xi)和抗渗比降g(xi),生成网络训练数据xi→{q(xi),g(xi)} (i=1,2,…,S)。

步骤4:设计RBF神经网络,以土体参数随机变量xi为输入变量,拟定高斯函数为隐藏层激活函数,出逸比降q(xi)和抗渗比降g(xi)为输出变量。

步骤5:采用训练数据xi→{q(xi),g(xi)}(i=1,2,…,S)训练网络至误差小于10%。

步骤6:根据不同年度下土体材料参数均值与变异系数,利用LHS随机抽样N次获得随机参数xi(i=1,2,…,N)。

步骤7:采用训练好的网络计算q(xi)、g(xi),其中i=1,2,…,N。

融合RBF神经网络和LHS方法优势,结合有限元求解土石坝时变渗透破坏概率的计算流程如图1所示。

图1 计算流程

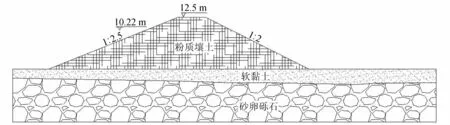
图2 土石坝断面结构示意图

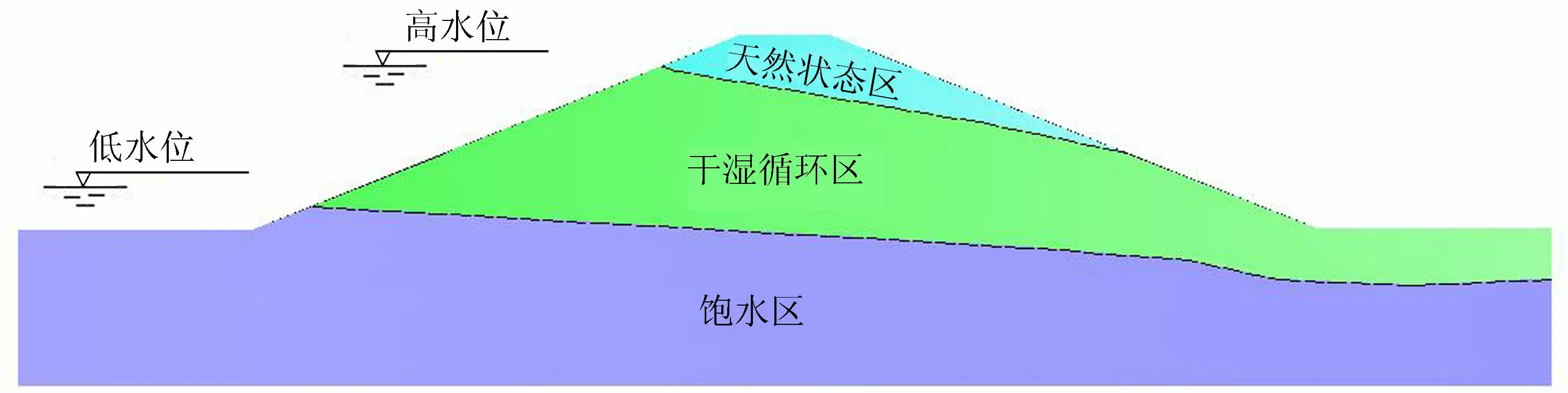
图3 土石坝水位变化影响分区

3 实例分析

3.1 基本概况

以西南某年调节水库土石坝典型断面为研究对象。该坝坝身平均高度为12.5 m,临水侧坡比为1∶2.5、背水侧为1∶2,历史最高水位10.22 m,坝身为粉质壤土,坝基为二元结构,上部为平均2 m厚软黏土,下部为8 m厚砂卵砾石,土石坝断面结构如图2所示。

3.2 参数时变规律

3.2.1力学指标时变规律

土石坝在一个年度内经历的水位升降变化可近似认为使土石坝土体经受了一次干湿循环作用过程,呈现出如图3所示的分区特征,处于高水位浸润线以上区域为天然状态区,不受干湿循环影响,其黏聚力和内摩擦角为一常数;低水位浸润线和高水位浸润线之间为干湿循环区域,土石坝易发生渗透破坏的部位正好位于这一区域,低水位浸润线以下部分为长期饱水状态区,黏聚力和内摩擦角基本稳定[9-11]。

为保证试验的可靠性,坝身壤土、坝基黏土均现场取样,制成均一性较好的重塑土样。试样的制备过程按照SL237—1999《土工试验规程》执行,通过干湿循环试验模拟自然环境下土石坝土体干湿交替的过程。将制备好的坝身粉质壤土与覆盖层黏土两种土样试件各分为7大组,分别模拟土料天然状态及干湿循环1、2、3、5、10、15次等状况,每大组再分为3个小组,每小组4件试样,采用直剪试验开展力学参数研究,粉质壤土与覆盖层黏土黏聚力与内摩擦角的变化规律如表1、表2所示。

表1 坝身壤土干湿循环试验值

从表1、表2中可以发现,土壤试样的黏聚力相较于内摩擦角随干湿循环次数增加降低更为明显,且黏土相较于壤土的衰减程度更突出,黏聚力与内摩擦角衰减均呈现较为明显的负指数相关性,因此采用双负指数函数来描述黏聚力与内摩擦角的劣化系数ζ(t)与干湿循环次数的关系:

ζ(t)=αe-χt+βe-ηt

(7)

式中:t为干湿循环次数;α、β、χ、η为待定系数,可通过试验值拟合得到。

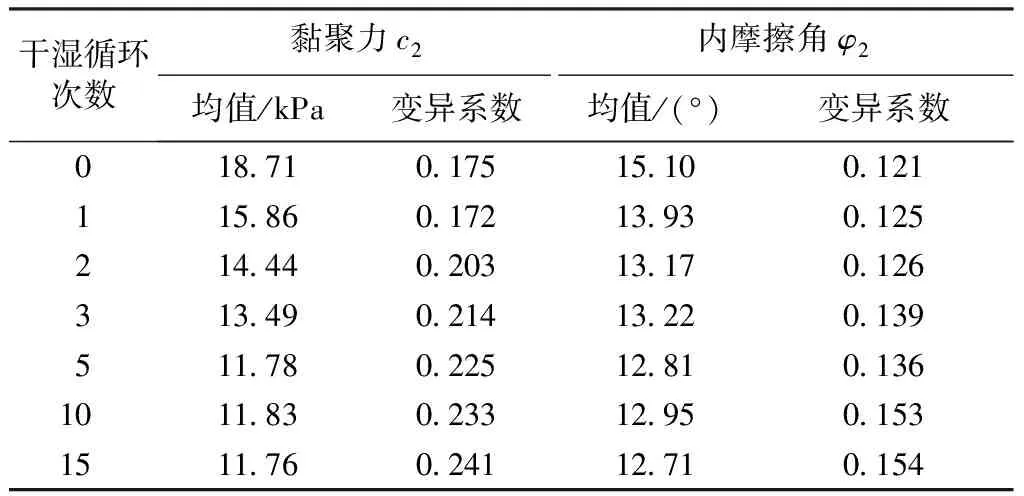
表2 覆盖层黏土干湿循环试验值

试验拟合结果如表3所示,壤土、黏土黏聚力和内摩擦角劣化系数拟合相关性系数R均大于0.95,黏聚力和内摩擦角的衰退过程可以用式(7)较好地表征。

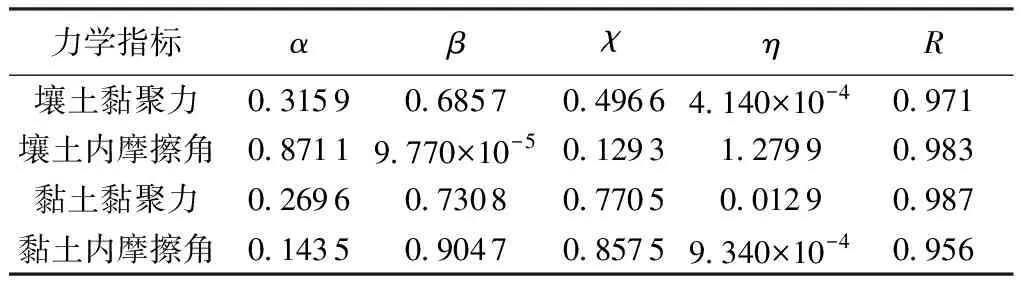
表3 壤土、黏土力学指标劣化系数拟合参数

此外土体强度的衰退规律也与力学参数的变异性相关。对于土体试样力学参数的变异性,根据试验结果,采用二次函数得到壤土、黏土的黏聚力和内摩擦角变异系数V(t)与干湿循环次数的关系,即

V(t)=αt2+βt+c

(8)

试验拟合结果如表4所示,壤土、黏土黏聚力和内摩擦角变异系数拟合相关性系数R均大于0.90,黏聚力和内摩擦角的变异过程可以用式(8)较好地表征。

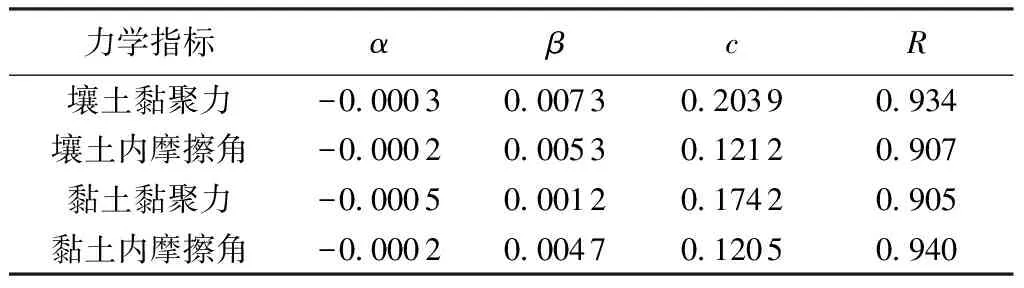
表4 壤土、黏土力学指标变异系数拟合参数

表5 大坝各分区渗透系数

3.2.2渗透系数时变规律

渗透系数反演时先根据地勘资料大致拟定材料的渗透系数范围。由于坝身壤土与坝基黏土渗透系数的变幅较大,且对渗流场有较大影响,因而主要反演壤土与黏土的渗透系数,各渗透系数的变幅区间见表5。采用文献[12]方法分年度反演平均渗透系数,反演结果如图4所示,从中可以发现随时间的推移,渗透系数呈现逐渐变小的趋势,这应与水体泥沙含量较高,泥沙在大坝迎水面逐年淤积堆厚形成防渗铺盖,致使土石坝渗透性减弱有关。

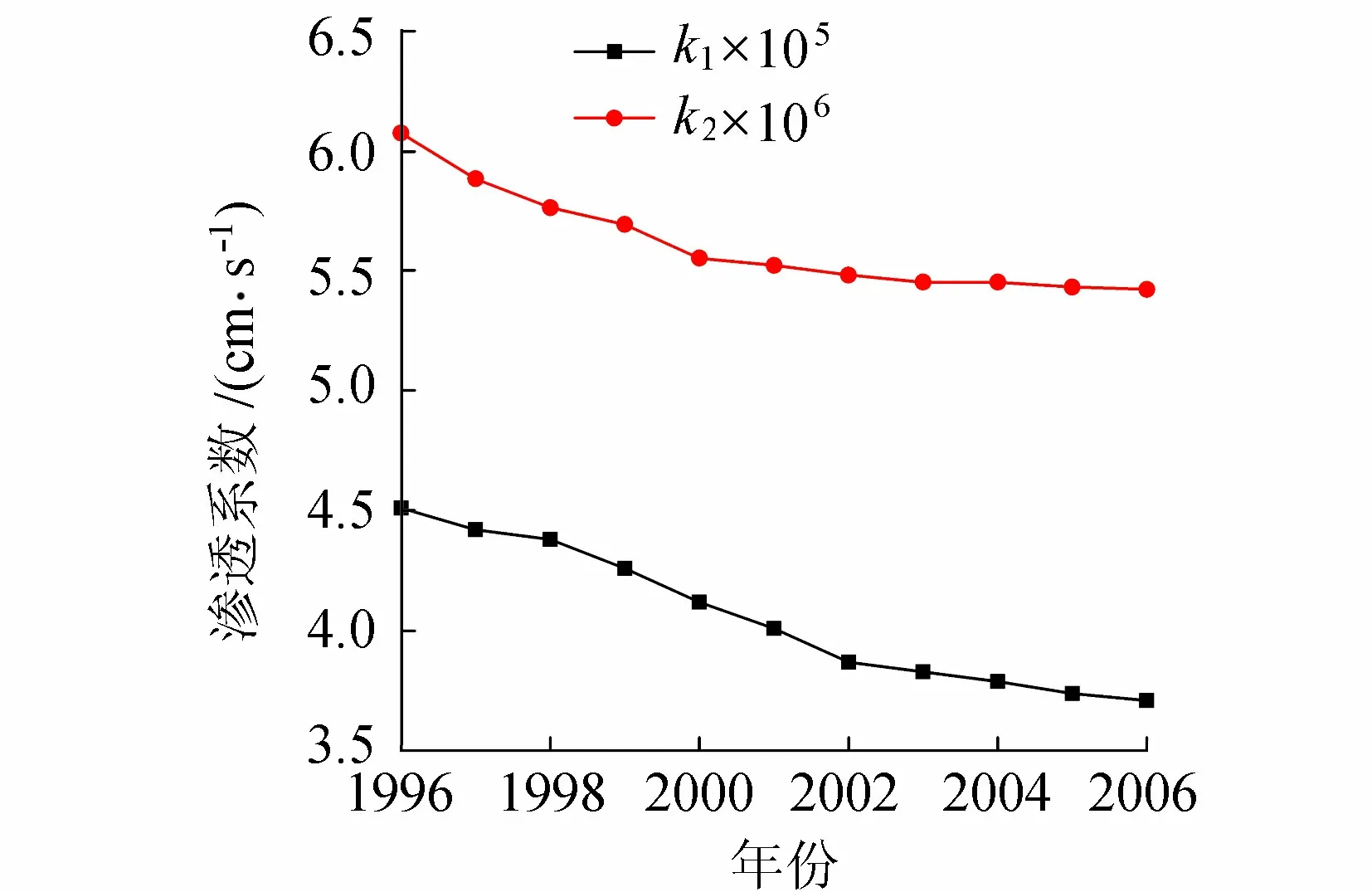
图4 渗透系数年度变化

3.3 土石坝时变渗透破坏概率

3.3.1土石坝渗流计算模型

根据土石坝标准断面建立有限元数值分析模型,取x轴为迎水坡指向背水坡方向,y轴竖直向上。模型范围分别沿x轴取92.00 m,沿y轴方向沿坝基取22.50 m。渗流计算时,背水面考虑无水,迎水面取历史最高水位10.22 m,水位以下坝身、坝基左右侧面作为第一类边界(水头边界),坝基底面作为第二类边界(无流量交换)。有限元模型包括节点1 126个,单元1 016个,如图5所示。

图5 典型断面有限元网格划分

3.3.2土石坝渗透破坏成果分析

根据图1所示计算步骤,采用干湿循环试验和渗透系数反演方法模拟土石坝材料参数的时变规律,选取土体参数500组数据进行有限元模型计算,生成训练数据,利用其生成的满足精度要求的RBF模型计算渗透破坏失效概率。其结果与传统Monte Carlo随机抽样法10万次渗透破坏失效概率计算结果对比如图6所示,从中可以看出两种计算方法渗透破坏概率差别很小,结果相吻合,验证了本方法的准确性与可靠性。本方法只需要有限元计算500次,与传统的Monte Carlo计算相比极大地减小了计算工作量。同时可以看出,随时间的推移,土石坝渗透破坏概率逐年增加并呈现早期增加较快,后期逐渐平稳的特点,这与土石坝渗透破坏发展的一般时效特性接近。

图6 土石坝不同土层时变渗透破坏概率

4 结 语

采用干湿循环土工试验与渗透系数反演手段,从土体材料参数的变异性与时变性的角度,通过RBF神经网络与LHS抽样相互融合的方法对传统的Monte Carlo随机抽样方法进行改进,在保留良好的计算精度的同时极大地减少了有限元计算次数,较好的模拟了土石坝结构渗透破坏概率发展的随机、时变特点。将该方法应用于某土石坝渗透破坏时变概率分析,结果表明该土石坝渗透破坏概率处在较高水平且呈现逐年增大的趋势,这与该土石坝最近一次安全鉴定的结论相一致,需要采用除险加固的补强措施来提高该土石坝洪水位期间渗流稳定性。