含植物水流动力特性研究进展
刘宏哲,娄 厦,刘曙光,钟桂辉,张 洪
(同济大学土木工程学院水利工程系,上海 200092)
植物是河流生态系统和海岸带湿地生态系统的重要组成部分。河道中的植物可以增加水流阻力,抬高水位,减缓水流速度,减小河道行洪能力,改变水流特性[1-2]。海岸带植物可以消减波浪能量,降低波高,影响波浪的传播[3]。植物对水流动力条件的改变进一步影响泥沙输运和物质扩散,在固沙促淤[4-5]、净化水质[6-7]等方面具有重要作用。近年来,含植物水流动力特性研究得到了广泛关注。大部分学者采用现场调查、原位试验、水槽试验、数值模拟等手段,针对植物密度、刚度和排列方式等植物特性对水流动力特性的影响开展了大量研究,在植物引起的水流阻力增加、水流结构变化以及波浪能量消减等方面取得了显著的研究成果。然而含植物水流影响因素众多,不仅受到植物特性的影响,还与水流断面形状、床面糙率、水位和流量等水流条件有关。含植物水流动力过程十分复杂,目前应用较多的仍为经验公式,理论基础尚未完善。本文从含植物河道水流阻力特性、水流结构和植物消波特性三方面综述了国内外含植物水流动力特性的相关研究,并对今后该领域的研究方向进行了展望。
1 含植物河道水流阻力特性
20世纪初,部分学者对含植物河道水流阻力特性进行了初步研究,认为水流条件(水深、流速)和植物特征(密度、高度、刚度、分布以及生长周期)等都对其有很大影响[8]。目前,国内外对含植物河道水流阻力特性的研究主要分为以下两类:①将植物与河床看作一个整体,研究纵向流速垂向分布规律,常通过Chezy阻力系数、Darcy-Weisbach阻力系数以及Manning系数描述,其中Manning系数应用最为广泛;②将植物看作障碍物,研究其对水流的阻碍作用和水流绕流引起的紊动作用,常用拖曳力系数来描述。
1.1 含植物河道Manning系数n
Manning系数是研究含植物河道纵向流速垂向分布的重要参数。从产生原因来看,Manning系数可分为床面糙率nb项、形态糙率nf项以及植物糙率nv项三部分,通常实际河道床面和水体断面形状基本不变(即nb和nf不变),植物糙率nv是其主要影响因素[9],研究表明Manning系数与植物淹没状态、密度和刚度等条件相关[10-12]。
早期含植物河道Manning系数的研究是为农业灌溉设施建设服务,这些研究大多采用实地勘测的方法,着眼于实际场地在自然植物覆盖情况下的整体糙率n。1949年Ree等[13]根据大量现场试验的数据绘制了n-VR(V为断面平均流速;R为水力半径)经验曲线,这样根据植物的类型、高度以及生长状态,河道平均流速和水力半径,可直接在该曲线上查出相应的n值。该方法应用简便,适用于对精度要求不是很高的工程建设,在美国灌溉设施建设中发挥了巨大的作用。然而,Kouwen等[14]指出n-VR曲线方法仅是试验数据的简单处理而没有科学的推导过程,并在其水槽试验中,发现同种植物条件(植物类型、高度等均一致)下n-VR点并没有落在单一曲线上,同时指出:坡度小于3%或者植物过于短小、稠密的情况下n-VR曲线方法精度很低。在实际运用n-VR经验曲线方法过程中,虽然考虑了河道形状、坡度,植物类型、高度以及生长状态的影响,但如何选择合适的n-VR曲线,依赖于主观经验,此外该方法并未明确考虑植物的淹没状态以及刚度对n的影响。
在研究刚性植物水流阻力特性过程中,植物常被简化为刚性光滑圆柱体。Li等[15]通过研究圆柱体后的涡旋,分析挺水植物对水流阻力的影响,发现水流阻力随植物密度的增加而增加,同时也受植物排列方式的影响。Petryk等[10]在其水槽试验中,基于均匀流动量平衡方程,提出了刚性挺水植物均匀分布于河道床面条件下,植物拖曳力为参数的含植物河道n的经验公式:
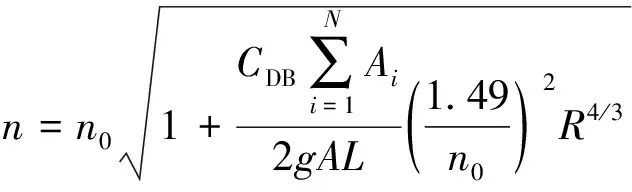
(1)
式中:n0为无植物河道Manning系数;CDB为沿流向植物平均阻力系数;Ai为第i棵植物在过流断面上的投影面积;N为所研究河段植物数目;g为重力加速度;A为过流断面面积;L为所研究河段植物带长度。该公式物理意义明确,可以定量地反映植物作用的影响,其计算的关键在于确定参数CDB[16]。Righetti等[17]在水槽试验中,以塑料羊毛球模拟沉水植物,研究了不同密度的梅花形布置植物对水流阻力的影响,并将式(1)得出的Manning系数通过数学模型进行了验证,结果表明式(1)的应用范围可扩大到柔性植物。
柔性植物在水流中存在倒伏和挺立两种状态。Ree等[13]认为,植物挺立时和刚性植物类似,n与植物密度和水流断面遮盖程度相关;随着流速增大,植物由挺立向倒伏渐变,n逐渐减小;当植物完全倒伏后,床面处于类似于水力光滑区或自光滑向粗糙的过渡区[18],n与流速相关。Kouwen等[11]在水槽试验中,采用苯乙烯条模拟柔性植物,提出了以柔性植物刚度和偏转高度为参数的n计算公式:
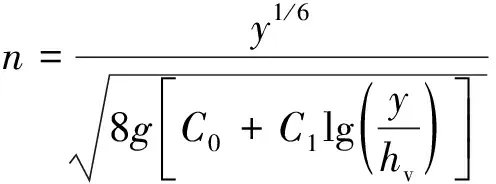
(2)
式中:y为水面高度;hv为植物偏转高度;C0、C1为反映植物性质的经验参数,与平均流速V和剪切流速u*之比有关。由于在野外hv难以采用观察法测量,Vedrana等[19]采用悬臂梁挠度理论计算植物在水流作用下的偏转高度,提高了式(2)的准确度。Stephan等[20]提出了基于声学多普勒流速仪(ADV)信噪比测量hv的方法,认为在植物偏转高度处,植物引起的水流散射会剧烈增加,导致ADV设备信号“噪音”突增,即信噪比最大处为hv。这些理论和方法的提出,对含柔性植物水流阻力的精确计算以及广泛推广有着重要的意义。
天然植物通常由刚性树干部分和柔性枝叶部分组成,对于植物柔性部分水流阻力的研究,初期仅将未完全偏转的植物看作刚性植物,完全偏转的植物看作柔性植物,这样的界定方式不明确,会导致计算方法难以选择。Kouwen[12]定量考虑植物的抗弯刚度,引入参数MEI(M为植物密度,E为植物弹性模量,I为植物横截面惯性矩),以此方式表达的Manning系数n可用下式导出:
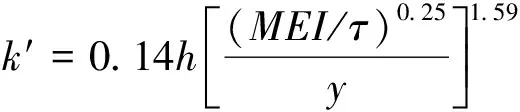
(3)
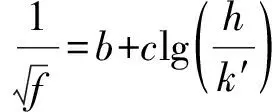

表1 单根植物拖曳力系数CDI经验公式
1.2 含植物河道拖曳力系数CD
拖曳力系数是计算植物引起水流阻力的重要参数,也对研究含植物河道纵向流速垂向分布、水流能量损失、泥沙及污染物输运有着重要作用。此外,拖曳力系数也可用于Manning系数的计算(式1)[16]。早期研究基于水流绕流作用原理,认为拖曳力来源于植物迎水面与背水面之间的压力差,据此Morsion等[21]提出了含植物水流阻力计算公式:
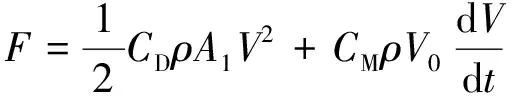
(4)
式中:F为植物受力;CM为惯性力系数;A1为植物迎水面积;V0为植物在水中的体积;ρ为水的密度。通常情况下惯性力项较拖曳力项小很多,在计算中通常被省略[19-23]。
1.2.1含单根植物河道拖曳力系数CDI
在最初的研究中,将单根植物视为挺立在水流中的光滑的圆柱体形障碍物。Clift[24]从尾迹流产生和发育的角度对其拖曳力进行了分析,给出了不同雷诺数范围内的CDI经验公式(表1)。Finn[25]在其试验中采用水流宽度与植物直径之比达1 500的大比例模型,得出了适用于雷诺数较小,无边壁影响的试验结果。Gao等[26]分析了液气两相混合流通过单根刚性圆柱状物体的试验现象,拟合得出了相应的经验公式(表1),对于风暴潮等极端气候条件下,孤立波冲击红树林产生拖曳力的研究有着一定的借鉴意义。Cheng[27]和Tang等[28]对比分析了不同学者拟合的CDI经验公式,利用众多学者的试验数据,分别拟合得出了适用于较大雷诺数范围的CDI经验公式(表1),两者对比可知Tang等拟合的公式适用范围更加广泛。单根植物拖曳力的影响因素较少,物理意义较为明确,研究者们多采用雷诺数作为关键参数,早期经验公式在其给定雷诺数范围内精度很高,后继学者则在统一经验公式表达式方面做了大量的努力。
由表1可知,在雷诺数较小的条件下(0
1.2.2含群体植物河道平均拖曳力系数CDB
直接应用单根植物拖曳力与植物数N相乘来计算植物群体阻力,由于忽略了水流紊动的影响,未考虑植物群的尾流遮蔽效应,会导致群体阻力计算结果偏大,使得水流时均流速预测结果偏小且有较大误差[15]。因此,部分学者将植物群看作一个整体,研究平均拖曳力系数CDB。
基于单位长度水体动量平衡原理,Petryk等[10]提出平均拖曳力系数计算公式:
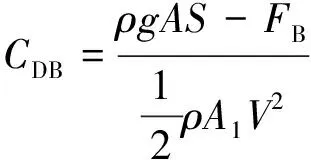
(5)
式中:S为水头损失;FB为河床及边壁阻力。该方法得到了广泛应用,Tanino 等[29]采用水槽试验,分析了刚性沉水植物随机布置条件下的水流拖曳力系数与雷诺数和植物密度的关系,并采用线性回归的方法,得出了一组不同试验条件下拖曳力系数的取值范围。Stone等[30]采用该方法时,考虑了流量不变的前提下,植物削减水流断面,从而引起作用在植物上的平均水流流速增大的影响,因此采用增大后的水流流速(V′=Q/(A-A1)),计算了不同水流条件及植物特征下的拖曳力系数。
除此之外,Fathi-Maghadam等[31]采用真实挺水植物进行大量试验研究,忽略表面张力的影响,运用量纲分析法,罗列了所有与水流阻力有关的参数,给出了层流和充分发展的紊流状态下,拖曳力系数函数关系式:
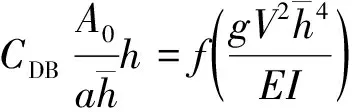
(6)
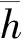
CDB=f(Re,λ,ξ)
(7)
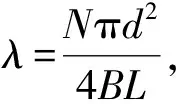
CDB=1.53[1+0.45ln(1+100λ)Re-3/50]
(0.002 2<λ<0.088 5)
(8)
Wang等[33]在不同水流条件,不同植物密度下进行试验,根据其水槽试验数据,拟合得出了刚性沉水植物矩形排列条件下,平均拖曳力系数计算公式:
(0.005<λ<0.014 13)
(9)
此外,部分学者研究了排列方式对植物拖曳力系数的影响:Nepf[34]采用随机、梅花形布置刚性挺水木棒进行试验,发现CDB随着植物密度增大而减小;Busari等[35]采用矩形布置半刚性木棒,加密植物(横向距离不变,纵向距离减小)时也得到了同样结论。Zukauskas等[36]将这种现象概括为遮蔽效应,即下游的植物处在较小的流速场中,同时紊流分布受到影响导致该处压力差也较小,所以下游植物的拖曳力小于上游。然而,Stone等[30]采用梅花形布置刚性沉水木棒,发现CDB随着植物密度增大而增大,Tanino等[37]采用随机布置刚性挺水木棒进行的试验、Kothyari等[32]采用梅花形布置刚性挺水钢棒进行的试验、Busari等[35]采用矩形布置半刚性木棒,加密植物(横向距离减小,纵向距离不变)进行的试验均得出了类似的结论。Busari等[35]将这种现象概括为通道效应,即当一株植物在另一株植物的水平方向(横流方向)时,过水断面会减小,断面流速由于连续性原理而增大,部分势能转化为动能,导致植物前后压力差增大,所以CDB增大。由此可知,CDB和植物密度之间的关系会受到植物排列方式及水动力条件的影响。
2 含植物河道水流结构
水生植物的存在极大地改变了河道中的水流结构。含植物河道中,植物根部产生的尾流与河床剪切紊流同时存在,植物层与非植物层之间的过渡区域存在水流脉动使得横向和纵向涡旋更为复杂。较无植物河道相比,含植物河道水流的纵向流速垂向分布和水流紊动特性都发生了很大的变化,继而影响泥沙等物质输运,因此研究含植物河道水流结构有着重要意义[38]。
2.1 含植物河道时均流速分布
在植物的影响下,水流的纵向流速垂向分布受到很大的影响,不再遵循典型的对数分布规律,存在着明显的分区。因此,大多数学者根据含植物河道水流纵向流速垂向分布的特征,对其进行分区研究。国内外学者大多采用两区和三区划分的方法,也有小部分学者持四区划分的观点[39-41]。
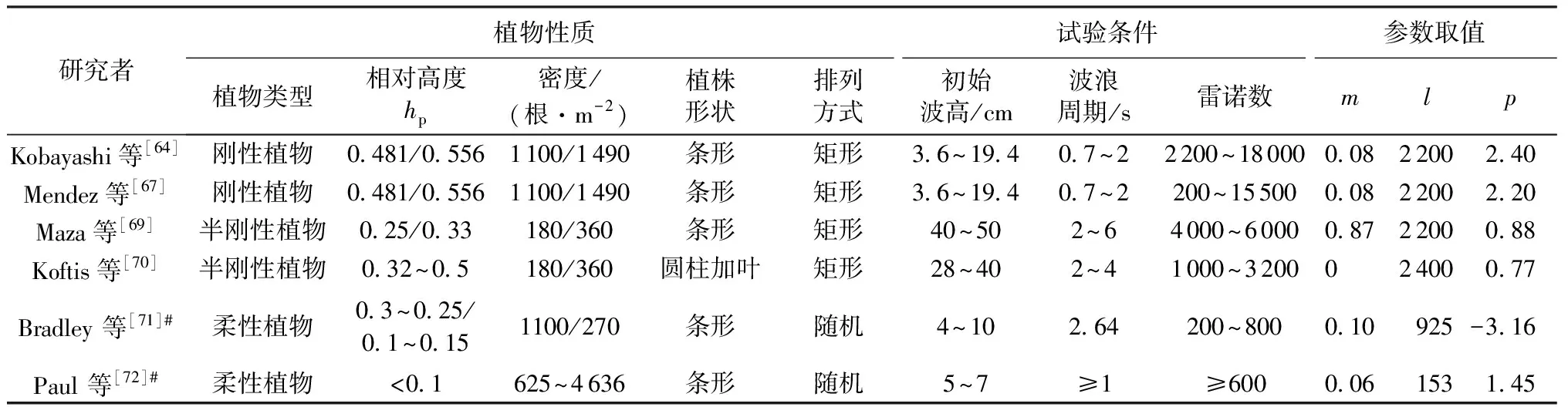
植物的存在造成植物层和非植物层水流阻力突变,因此两区划分将流速分布分为植物层和植物上层。在植物层内(0 (10) 式中:u为距河床底距离为z处的水流流速;kv为卡门系数,取0.4。 在植物上层,Kouwen等[14]采用Prandtl的混合长度理论,结合水槽试验数据得出: (11) 式中:C为积分常数。亦有其他学者得出了植物上层水流流速符合对数分布的结论[42-44]。 三区划分一般是在两区划分的基础上增加植物顶部附近的过渡区,国内外不同学者得出的三区分区界限及拟合的流速分布特征见表2。 基于现象的定性描述,Gourlay[45]早期研究的结果大致地给出了各区流速的特点,在两区划分的基础上增加了河床底部附近,流速为较小常数的第一区。基于水力学方法,时钟等[46]对含真实柔性植物水流进行试验研究,采用局部摩阻流速、粗糙长度、冠层粗糙雷诺数、床面剪切力对流动区域进行描述,发现冠层区域和自由水面区域之间存在着流速梯度变化很大的过渡区,并提出随着试验条件的改变,可能存在内、外两个边界层。采用掺混理论,槐文信等[47]采用PVC模拟柔性植物,ADV测量纵向流速, 表2 纵向时均流速u垂向分布三区划分 注:uhv为植物弯曲高度处纵向流速;Y1和Y2为Carollo等[48]提出的三区划分的两个重要的界限参数,Y1 提出了反映河道水流被“压缩”现象的方法,并给出了u的经验公式。Carollo等[48]分别量测了3种不同真实植物下u垂向分布,并根据试验数据拟合了经验公式。诸多学者虽然采用不同的推导方法,但三区划分结果相类似,都是对植物区域水流阻力变化很小、植物顶端附近区域水流阻力存在拐点以及植物上层区域水流阻力很小这一现象的解释。 也有学者持四区划分的观点,Baptist等[40]根据水槽试验提出了含刚性沉水植物水流的四区划分方法,自下而上依次为,第一层靠近河床底部(流速符合对数增长)、第二层植物层内部远离河床底部(流速均匀)、第三层植物层顶部过渡区域(流速符合指数函数)、第四层植物层上部(流速符合对数分布)。Huai等[41]对含浮水刚性植物水流进行了大量的试验,提出了四区划分的观点,自下而上依次为,流速对数增加的无植物下层、流速减小的无植物上层、流速线性减小的植物内层和流速梯度几乎为0的植物外层。浮水植物相对高度越小,无植物下层流速对数增长越接近于无植物水流,此时流速减少的无植物上层也发育较为完整,在植物层和无植物层的交界处,水流阻力突变,植物刚度、密度越大,流速减小越快,减小到一定范围内,进入植物外层区,流速几乎不变。 由于植物种类、形态、密度、相对淹没度等植物特性以及断面平均流速、水深等水流条件的复杂性,研究者虽采用同样的理论方法进行研究,却得到了不同的拟合结果,导致速度分区方式众多,经验公式也各不相同,很难用统一的方式描述u垂向分布。诸多学者将分界点取在植物的有效高度处附近,分界点以下为流速变化较小的植物区域;分界点附近为流速剧烈变化的过渡区域;分界点到自由液面为u垂向分布与无植物情况类似的植物上层区域。刚性植物的分界点在有效高度处以上,而柔性植物的分界点则较低,这是因为刚性植物水流阻力的转折点在植物的顶端,柔性植物水流阻力的转折点则在植物有效高度以下;植物密度越大分界点越高,这是因为密度越大的植物水流阻力的变化越大。因此,确定植物特性、水流条件与u垂向分区间的定量关系,建立综合考虑两方面因素的数学模型,是今后一段时间的研究重点。 水流的紊动特性是影响物质输运的关键,描述水流紊动特性的主要参数有紊动强度、雷诺应力等。与无植物河道相比,含植物水流紊动强度和雷诺应力分布发生了很大的变化,其影响因素主要有植物的种类和类型、刚度、密度以及淹没程度等。 在植物层与非植物层交界处,水流紊动交换强烈,水流流速出现拐点[14],紊动强度与水流流速梯度正相关[49],故紊动强度最大值在此处出现。Lopez等[50]通过ADV测量含刚性木棒水流流场,也得到了同样的结论。闫静[51]对含刚性植物水流流场进行了量测,分析得出植物上层区域,雷诺应力的分布与淹没度有关,较小淹没度时遵循指数规律,较大淹没度时遵循线性规律。吴福生[52]在其试验中对比了刚性、柔性植物对水流紊动特性的影响,认为水流含刚性植物较柔性植物有着更大的紊动强度。Wilson等[53]对比了有叶植物与无叶植物对水流紊动特性的影响,认为有叶植物紊动强度和雷诺应力的最大值出现位置较高。李艳红等[54]通过试验数据分析指出,柔性植物的紊动强度受流速梯度、平均流速及植物密度影响较大,受植物高度影响较小,水流紊动强度最大值始终出现在植物冠层上方附近,并给出了紊动强度σ的经验公式: (12) 式中:c为参数,与植物密度相关。陈界仁等[55]分析了含柔性沉水植物水流紊动特性,观察到紊动强度和雷诺应力最大值均出现在植物顶层位置,且植物密度越大,水流紊动强度和雷诺应力最大值也越大;断面平均流速越大则水流紊动强度、雷诺应力随之增大;植物层与非植物层间的过渡区域内,存在着剧烈的能量交换和剪切作用,这两种作用在非植物层随水深增加而减小,在植物层内随水深增加而增大。 刚性、柔性植物密度越大紊动强度和雷诺应力就越大;柔性植物对水流紊动强度的影响较刚性植物小,紊动强度最大值的出现位置在植物顶部以上也较刚性植物高,这可能是因为刚性植物交界处边界条件突变而柔性植物倒伏产生类似边界层的区域,会引起剪切区域上移。有叶植物由于含有柔性部分,介于刚性植物和柔性植物之间,紊动强度最大位置也出现在植物顶部以上。此外,Huai等[56]直接从能量交换角度出发,发现植物区域能量会转移到无植物区域,且受植物的密度、雷诺数及淹没程度的影响;吴福生[52]通过ADV、PIV获得涡量场分布,通过特征拟熵描述能量耗散规律,得出植物冠层处,特征拟熵达到峰值的结论。 植物是海岸带湿地生态系统的重要组成部分,波浪传播至海岸带植物区域时,受到植物的阻碍,波能衰减,波高降低。大量学者从消波系数和能量衰减系数两个方面,研究了不同波要素条件下植物对波浪传播的影响。 植物消波系数是从波高衰减角度描述植物的消波作用。颜学恭等[57]分析了长江中下游不同类型防浪林林带结构的消波效果,认为防浪林林带越宽、长势越好、水下体积越大消波效果越好。消波系数K定义[58]为:K=1-H1/H0,其中H0为入射波波高;H1为植物区波高。该系数得到了广泛的应用,章家昌[58]采用野生篙草模拟天然灌木林,在其水槽试验中分析有叶植物的消波特性,拟合出了K的经验公式: (13) 式中:α′、α″分别为描述植物区域盖度的参数,0≤α′≤1.0,0.000 6≤α″≤0.009 1;R0为树干平均直径;R1为树干和树冠平均直径;2L0为波长。 基于大量的试验研究,发现波浪在互花米草等柔性植物中传播2.5 m后波高衰减40%,传播距离超过30 m后波高衰减达到94%[59],但当波浪较高时,会引起柔性植物剧烈运动,消波能力减弱;红树林等刚性植物的平均消波系数为13%,最大消波系数可达47%[60]。柔性植物和刚性植物对于波浪都有一定的消减作用,柔性植物消波作用远小于刚性植物[61]。但在实际观测中,对于波高较小的波浪,柔性植物的消波系数更大,这是因为互花米草等柔性植物在海岸带的密度远大于红树林等刚性植物。植物带宽度是消波能力的重要影响因素,一定范围内消波系数随着防浪植物带宽度增加线性增大,增大到一定数值后,消波系数基本不变[62];同时植物的高度对于消波能力的影响也较大,当植物茎叶区域高于液面时,有着较好的消浪效果,但当涨潮时植物被海水淹没,植物的摇摆与波浪的波动趋于同步,由于共振现象的发生甚至会观测到波高增加的现象[60]。 部分学者从能量角度出发,以消能系数的方式考虑了波浪通过植物区域的反射、衍射以及破碎现象,提出能量耗散模型,模拟波浪消减。Dalrymple等[23]利用小直径圆柱体模拟刚性植物,分析震荡流和植物之间相互作用引起的波能损失,给出了规则波条件下,时均波能损失的计算式: (14) 式中:εv为植物引起的能量消散系数;β为拟合系数,β=2/3π;k为波数;ω为波浪角频率;α=h/y,H为波高。其中拖曳力系数CDB为关键参数,式(14)可以较为精确地分析小范围区域的波能损失,然而却忽略了波浪、水流以及海床之间的相互关系。Möller等[63]监测了North Norfolk地区盐沼地的波高,发现通过盐沼区域,平均能量耗散系数可达82.05%,在无植物区域此系数也达到了53.53%。同时,Möller等[63]建立了考虑植物、水流黏滞作用、海床的渗流作用以及底摩阻力和浅水效应的数学模型,模拟结果与实地监测数据拟合较好。Kobayashi等[64]在式(14)的基础上,认为波高按指数规律衰减,提出了基于水平及垂直方向动量平衡的植物区域自由液面方程: (15) 表3 不同条件下参数取值 注:#为野外观测,其余为水槽试验。 拖曳力系数CDB是波能耗散模型中的重要参数,部分学者通过水槽试验和野外观测分析了能量耗散与植物密度的关系,得出了不同雷诺数条件下的拖曳力系数CDB计算公式: (16) 式中:m、l、p分别为常数项、系数项和指数项,表3中给出了不同条件下各参数取值。对于刚性植物,雷诺数取值在2 200~18 000范围内时,拖曳力系数范围为0.086~1.08[64]。半刚性植物所处状态分为挺立和倾斜两种,挺立状态,雷诺数在1 000~3 200范围内时,拖曳力系数可达0.801~1.96[71];倾斜状态,植物雷诺数在4 000~6 000范围内时,拖曳力系数的取值范围为1.28~1.46[69]。柔性植物有倾斜和倒伏两种状态,倾斜状态,植物雷诺数在200~800范围内时,拖曳力系数范围为0.108~0.732[70];倒伏后,植物雷诺数不小于600时,拖曳力系数小于0.198[72]。消波能力最强的是含茎叶的半刚性植物,消波能力最差的是柔性植物。刚性植物在水中基本不动,以冲击的形式消耗波浪的能量;半刚性有叶植物的刚性部分对于波浪具有消减作用,同时茎叶的摆动也会消耗波浪的能量;而柔性植物尤其是倒伏后的柔性植物,随着波浪运动,对波浪几乎没有消减作用。 此外,Mendez等[67]根据水槽试验结果,考虑拖曳力与惯性力的相对大小,认为使用Kc及植物相对高度为参数的平均拖曳力系数,较以雷诺数为参数的拖曳力系数更有效: (17) 式中:Kc=uTp/d,Tp为波浪周期。Zhang等[68]采用式(17),建立了二维波流耦合数学模型,分析了海岸带波浪和波生沿岸流的运动特征,模拟结果与水槽试验有着较好的拟合效果。 含植物水流动力特性问题中,水流阻力、水流结构和波浪消减是目前研究的重点,波流耦合条件下的波流植物共同作用研究逐步受到重视。在此基础上可进一步研究含植物水流中泥沙以及物质的输运规律,进而解决含植物河道、海岸带湿地泥沙输运和生态修复等问题。从目前国内外的研究情况看,以下问题仍需进一步深入探讨: a. 含植物河道水流阻力特性的研究中,植物有效高度的确定和刚度的计算,植物刚性、柔性配比,排列方式等诸多因素对植物拖曳力系数计算产生的影响仍需大量的试验和分析工作。 b. 含植物河道水流结构的研究,需要考虑含植物水流的三维特性,需对各向异性的紊流特征进行分析。 c. 考虑实际情况下的植物特征及波流耦合条件,需建立更精细的、符合实际情况的含植物波流耦合数学模型,以解决实际含植物水流及水环境相关问题。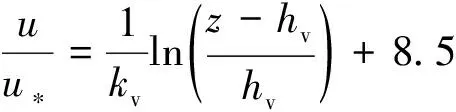
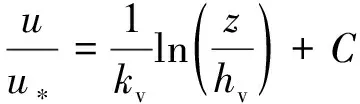

2.2 含植物河道水流紊动特性
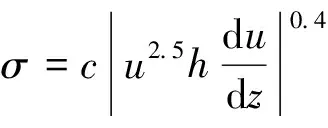
3 植物消波特性
3.1 消波系数
3.2 能量耗散
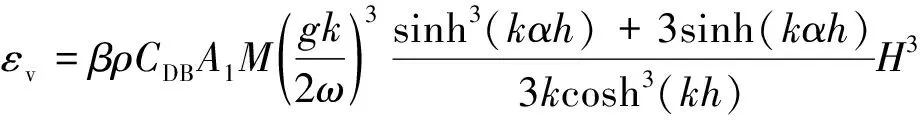
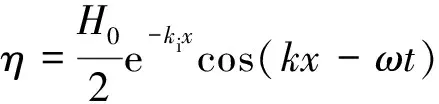
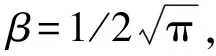
3.3 波浪作用下植物拖曳力系数CDB
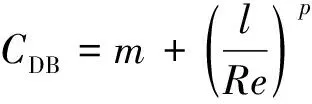
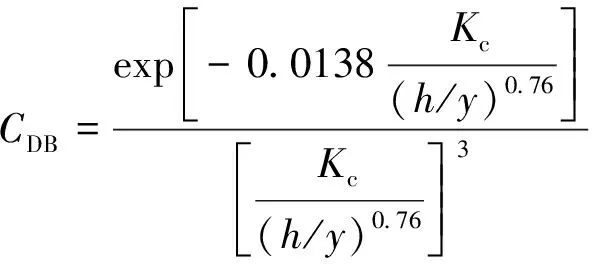
4 研究展望

