基于最小均方差拟合的QAM调制识别器

张立民，谭继远，闫文君

(1.海军航空大学信息融合研究所,山东烟台 264001;2.海军航空大学研究生一队,山东烟台 264001)

0 引 言

近年来无线通信技术的迅猛发展对数据传输速率、传输效率和频带利用率提出了更高的要求。选择高效可行的调制解调手段，对提高信号的有效性和可靠性起着至关重要的作用[1]。随着通信技术的发展，通信信号的调制方式也多种多样，当对接收信号进行解调或消除未知干扰信号时，我们需要先对信号进行调制识别。因此调制识别在许多领域有着广泛的应用,例如电子战,电子干扰和频谱检测等领域[2-3]。

目前调制识别的方法主要分为三种：基于似然的识别方法、基于特征值的识别方法和基于深度学习的识别方法[4]。基于似然的识别方法应用最广的是基于最大似然的调制分类器[5-6]，该方法识别率最高，但是计算量大，计算复杂度高。特征值的识别方法主要是基于高阶累积量的识别[6-7]，相比于似然识别，计算较为简单，但是识别率比基于似然的低。基于深度学习的识别方法还未发展完善，训练模型和训练样本的生成与选择会严重影响识别效果。目前调制识别研究的难点和热点主要集中在以下三个方面[8]：一是如何在非理想条件下进行调制识别[9-11]；二是如何改进基于特征值的调制识别[12-15]；三是如何构造一个简单有效的神经网络模型与训练样本进行调制识别。Aslam等利用遗传编程和K阶最近邻(KNN)分类器，选择累积量作为特征进行分类[16]，具有良好的分类性能，但是算法复杂度较高。Dobre等提出了基于秩序统计的低复杂度自动调制分类[17]，但是在分类性能和计算复杂度之间需要有一个权衡。近年来，基于神经网络的方法也广泛应用于调制识别[18][19]，Timothy等提出了利用卷积神经网络(CNN)进行调制识别[18]，在低信噪比和样本数较少的情况下，该算法变现出良好的性能，但是需要提前进行神经网络训练，大量有效的训练样本的生成还需有所改进。王方刚等首次提出了基于经验累积分布函数的KS检测(Kolmogorov-Smirnov test)方法[13]，并对其进行了改进，提出了基于折叠经验累积分布函数(cdf)的调制识别[1]，该方法主要讨论了在加性高斯白噪声条件下对接收信号进行识别，识别率得到了一定的提升，但是该论文未对加信道条件下的调制识别进行详细的讨论。

考虑信道参数对调制识别的影响，本文提出了基于折叠经验累积分布函数(cdf)的最小均方差的识别方法，对瑞利时不变信道下的信号进行调制识别。首先建立了经过信道和噪声的QAM调制信号模型，然后对接收信号的cdf0和标准调制信号的cdfk(k=1,2,3分别对应4-QAM、 16-QAM和 64-QAM)进行折叠，利用最小均方差准则判断检测信号折叠后的cdf0和cdfk的拟合程度，均方差小的，拟合程度高，从而达到调制识别的目的。

1 信号模型和方法描述

1.1 信号模型

假设接收信号的模型为

yn=Hxn+ωn,n=1,2,3,…,N

(1)

其中yn为接收信号，H为衰落信道，xn为复数发射调制符号，ωn为时刻n处的噪声采样，为加性循环复高斯白噪声。 传输的符号xn是4-QAM、 16-QAM或 64-QAM理想调制中的星座图点组成的序列，该星座属于一组调制格式{M1,M2,…Mk}。假设信道H为时不变瑞利信道，循环复高斯白噪声ωn～N(0,σ2)，因此ωn的实部和虚部独立同分布，且分布服从N(0,σ2/2)考虑单位功率星座，因此信噪比SNR=1/σ2。调制识别就是研究接收信号{yn},n=1,2,3,…,N为何种调制方式问题。

1.2 基于cdf的最小均方差准则

当对接收信号{yn}进行调制识别时，我们可以找到关于{yn}的一个特征序列{zn}，当进行PSK调制识别时， {zn}可以是信号相位；当进行QAM调制识别时，{zn}可以是信号幅度或者信号的实部和虚部[10]。然后计算关于{zn}的经验累积分布函数F0和理论的理想4-QAM、 16-QAM、 64-QAM调制{zn}的经验累积分布函数Fk,k=1,2,3，其中k=1,2,3分别对应4-QAM、 16-QAM、 64-QAM三种调制方式。接下来对上述cdf进行折叠，使不同调制的cdf之间有明显的区别。最后，利用最小均方差准则分别计算折叠后的F0和Fk,k=1,2,3之间的均方差，计算公式如下，

(2)

其中，Ek代表均方差，F0(zn)和Fk(zn) 分别代表特征序列{zn} 折叠后的cdf和折叠后的理想cdf。

根据最小均方差准则

r=argmin(Ek),k=1,2,3

(3)

均方差越小的，表示两者的cdf拟合程度越高，取三者中均方差最小的即为拟合程度最高的，其所对应的调制方式即为所接收信号的调制方式。

2 QAM调制识别

对于QAM调制识别，4-QAM、 16-QAM和 64-QAM调制的单位能量星座的信号点集合分别为

-1,1,3,5,7}

(4)

对于QAM调制信号，信号的虚部和实部相互独立且同分布，因此可以将接收信号yn的虚部和实部组成特征序列{zn}，z2n-1=R{yn}，z2n=I{yn}(R{·}、I{·}分别代表复数的实部与虚部)，对于上述系统模型，因为噪声ωn为循环复高斯白噪声，其实部与虚部独立同分布于N(0,σ2/2)，因此{z2n}的实部与虚部也独立同分布。

E(z2n-1)=E(z2n)=E(R(yn))=E(I(yn))=

E(R(Hxn+ωn))=E(I(Hxn+ωn))=

E(R(Hxn))+E(R(ωn))=

R(Hxn)

(5)

其中，E(z2n) 表示求{z2n} 序列的均值，H代表信道参数。

D(z2n-1)=D(z2n)=D(R(yn))=D(I(yn))=

D(R(Hxn+ωn))=D(I(Hxn+ωn))=

(6)

其中，D(z2n)表示求{z2n}序列的方差。

因此，z2n～N(0,σ2/2)。z2n的pdf为

(7)

其中x∈R{Mk}指的是信号的实部，H代表信道参数。将pdf经过积分得到关于z的cdf为

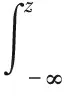
(8)

此时，未经过折叠的pdf和cdf如图1所示

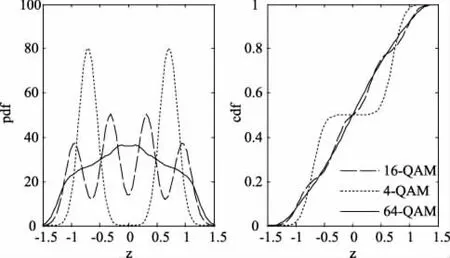
图1 未折叠的pdf与cdf

从图中可以看出，三者的pdf区分度不是特别高，特征不明显。接下来，通过折叠，使得三者的pdf更容易区分。

因为上述pdf关于z=0对称，接下来将pdf沿着z=0对折，得到一次折叠的pdf[1]如下

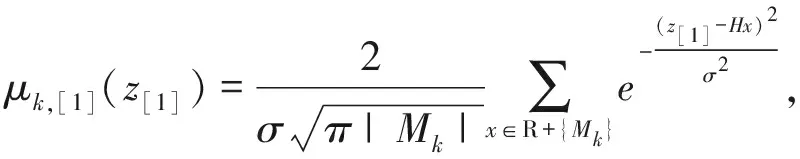
z[1]≥0

(9)

其中z[i]代表第i次折叠后的特征序列。

当z[1]≤0时，μk,[1](z[1])=0。将一次折叠的pdf[1]经过积分得到关于z[1]的cdf[1]为

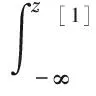
(10)

其中，x∈R+{Mk}指的是星座点的正实部，经过一次折叠后的pdf[1]和cdf[1]如图2所示。

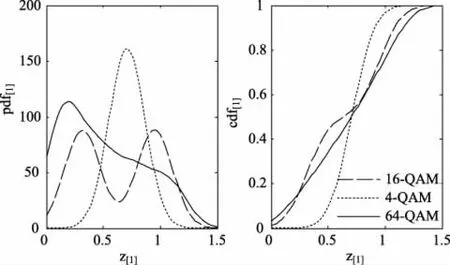
图2 经过一次折叠的pdf[1]与cdf[1]

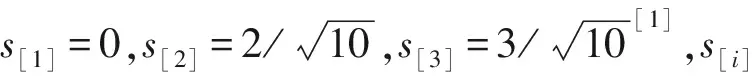
其中输入决策z[i]与s[i]关系如下

z[i+1]=|z[i]-s[i+1]|+s[i+1]

(11)

经过二次折叠的pdf[2]如下

μk,[2](z[2])=μk,[1](z[2])+μk,[1](2s[2]-z[2]),

z[2]≥s[2]

(12)

z[2]≤s[2]时，μk,[2](z[2])=0。将二次折叠的pdf[2]积分得到cdf[2]如下

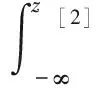
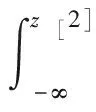
(13)

经过二次折叠的pdf[2]和cdf[2]如图3所示。

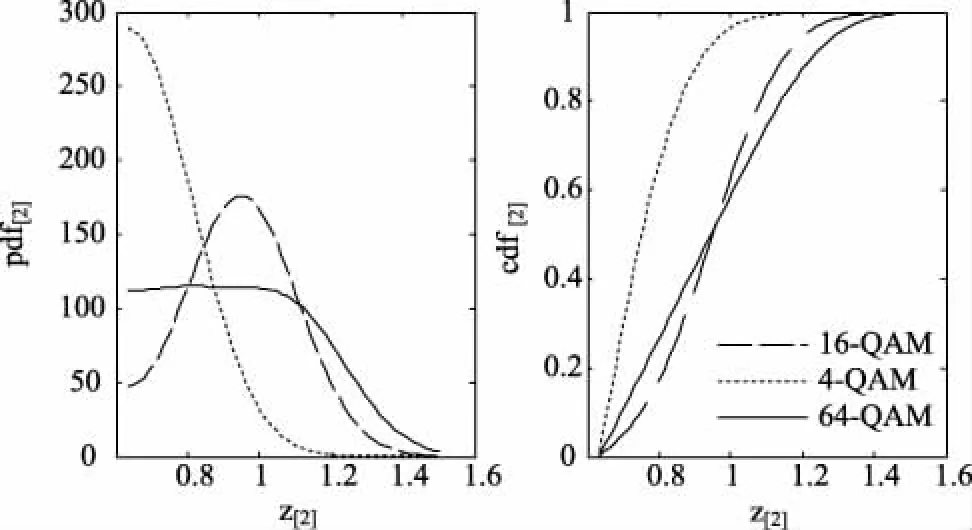
图3 经过两次折叠的pdf[2]与cdf[2]

从图中可以看出经过两次折叠的pdf[2]分为两个区域,其中一个区域4-QAM的pdf[2]较大，另一个区域16-QAM和64-QAM的pdf[2]较大。积分后两次折叠的4-QAM的cdf[2]和两次折叠的16-QAM、64-QAM的cdf[2]的区分度较大，这时用到最小均方差准则计算出给定样本的二次折叠cdf[2]与两次折叠4-QAM的cdf[2]、两次折叠的16-QAM的cdf[2]的均方差E1,[2]和E2,[2]，若E1,[2]E2,[2]，则信号采用的是16-QAM或者是64-QAM。这时需要对pdf[2]进行第三次折叠，使得折叠后的16-QAM和64-QAM的pdf[2]区分度明显，三次折叠的pdf[3]与cdf[3]表达式如下

μk,[3](z[3])=μk,[2](z[3])+μk,[2](2s[3]-z[3]),

z[3]≥s[3]=μk,[1](2s[2]-2s[3]+z[3])+

μk,[1](2s[3]-z[3])+μk,[1](2s[2]-z[3])+

μk,[1](z[3])

(14)

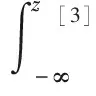
(15)

经过三次折叠的pdf[3]和cdf[3]如图4所示。

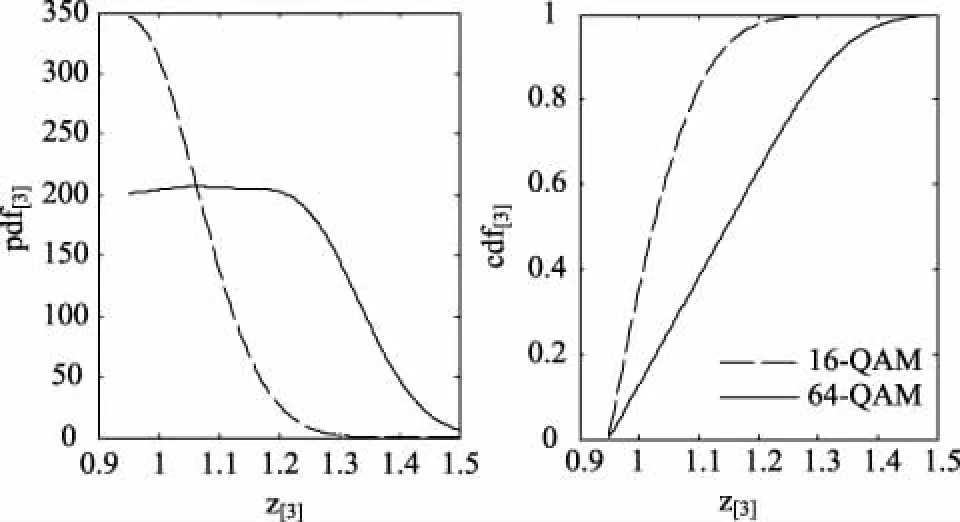
图4 经过三次折叠的pdf[3]和cdf[3]

此时再一次用到最小均方差准则判断拟合程度,若E3,[3]>E2,[3]则为16-QAM调制，否则，为64-QAM调制。

检测算法可以归纳为图5所示的决策树。

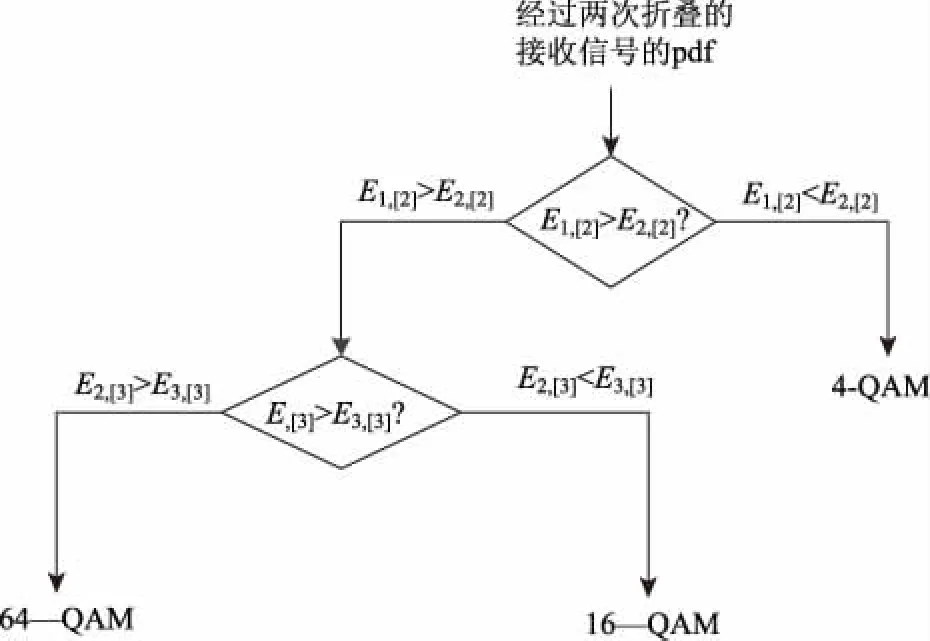
图5 最小均方差方法决策树

3 仿真和结果

3.1 仿真条件

仿真经过1000次蒙特卡洛仿真，接收信号时为随机产生的QAM调制信号，无特殊说明，仿真条件设置如下：样本数N=4000，调制信号xn为随机产生的序列，H信道模型为时不变瑞利信道，信噪比定义为SNR=10log10(1/σ2)

在实验中，采用正确的识别概率P衡量算法的性能

p=(λ=ξ|ξ),ξ∈Ω

(16)

Ω={4-QAM,16-QAM,64-QAM}

3.2 AWGN信道下，不同SNR时该算法对4-QAM和16-QAM调制的正确识别概率

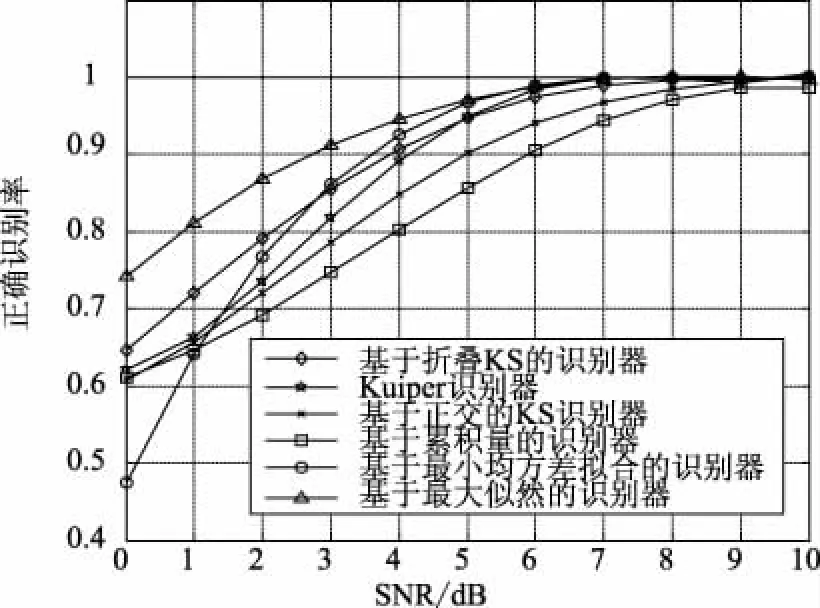
图6 AWGN条件下，不同分类器对4-QAM和16-QAM调制的正确识别概率

由上图可知，在只加高斯白噪声的情况下，当信噪比小于2 dB时，该算法性能较差。但当信噪比大于2 dB时,算法表现出良好的性能，并且在信噪比达到3 dB时,正确识别率由于基于折叠KS的识别方法，并且能快速达到最佳识别效果。

3.3 瑞利信道下，不同SNR时不同分类器对4-QAM、16-QAM和64-QAM调制的正确识别概率

对信号在默认条件下进行仿真,不同识别方法对QAM调制的正确识别概率如图7所示，由仿真结果可以看出相同SNR情况下，文中所提出的基于折叠cdf的最小均方差识别方法识别率绝大多数最高，且低信噪比情况下，识别概率较其他方法有明显的提高。随着SNR增大，识别率增大，当SNR=20 dB时，最大识别率便可以达到95%，而其他方法在SNR=25 dB时，识别率才达到最大。并且在高SNR下比基于累积量的分类器的性能明显好，较基于累积量的识别算法，最大识别率提高了5%。

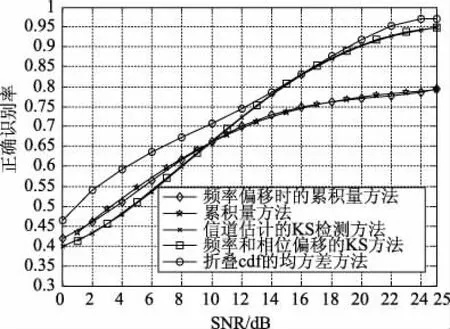
图7 不同SNR时不同分类器对QAM调制的正确识别概率

3.4 瑞利信道下，样本数对4-QAM和16-QAM调制的正确识别概率的影响

在不同样本数的条件下对4-QAM和16-QAM调制的正确识别概率如图8所示，可以看出，算法的正确识别率随着样本数N的增大而增大。并且随着N的增加，算法的收敛性和正确识别率都得到了提高。

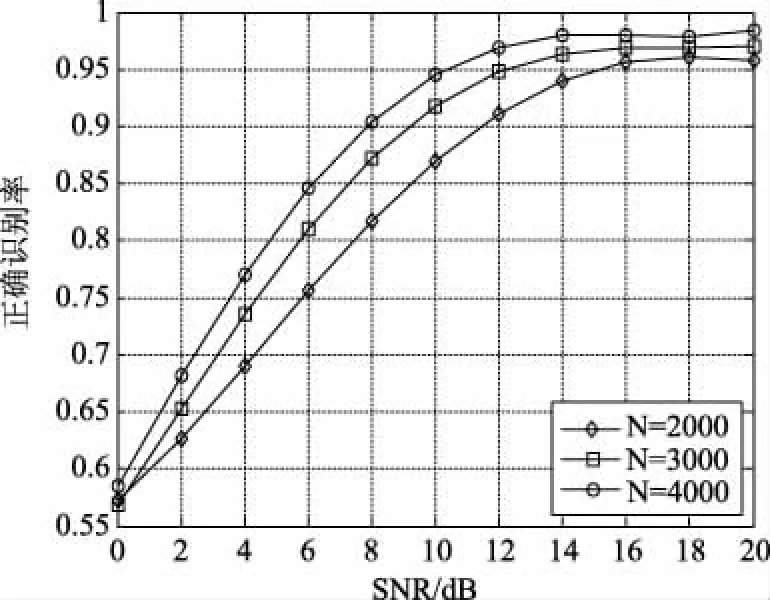
图8 不同样本数时对4-QAM和16-QAM的正确识别概率

3.5 瑞利信道下，样本数对4-QAM、16-QAM和64-QAM调制的正确识别概率的影响

在不同样本数的条件下对4-QAM、16-QAM和64-QAM调制的正确识别概率如图9所示，可以看出，算法的正确识别率随着样本数N的增大而增大。这是由于样本数N增多，pdf和cdf的统计特性会更加明显，更加有利于拟合程度判断。在样本数N=4000时，算法在低信噪比的识别概率得到了明显提升。

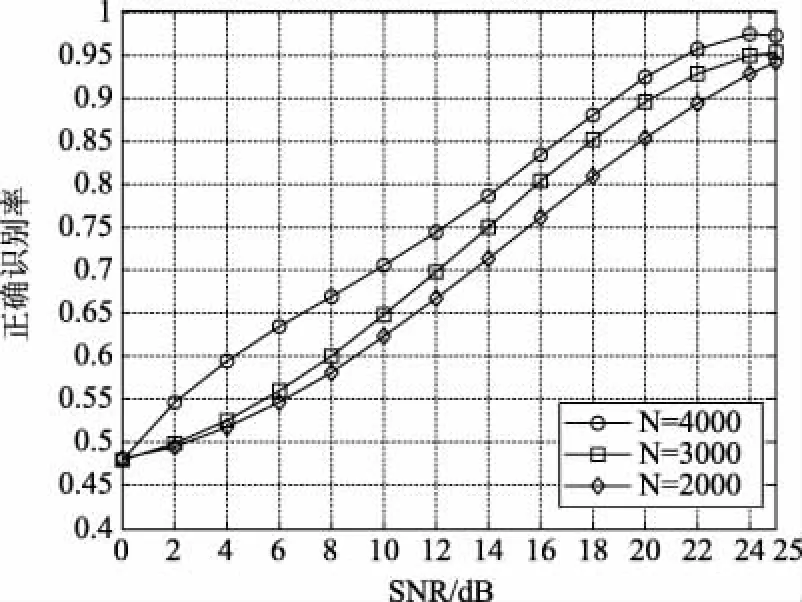
图9 不同样本数时的对4-QAM、16-QAM和64-QAM的正确识别概率

3.6 复杂度分析

3.6.1算法运行时间分析

表1 不同识别方法的识别时间表

比较了基于累计量识别、基于KS识别[13]、基于最大似然识别[4]本文算法的复杂度。从上表中可以看出，基于累积量的识别方法耗时最短，但是根据图6仿真可以看出识别效果较差。基于最大似然的识别耗时最长，但是该算法的识别效果最佳，本文算法折中了两者，在保证一定的识别效果的同时，识别时间得到了改善。虽然识别时间并不直接反映算法的复杂度，但是从一定程度上也反映了算法的复杂度[17]。

3.6.2算法复杂度分析

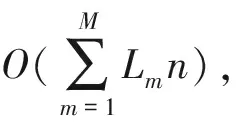
4 结 语

本文研究了4-QAM、16-QAM和64-QAM的调制识别问题，考虑了信道以及噪声的影响。本文方法基于最小均方差拟合，对QAM调制进行识别。建立了QAM调制的信号模型，推导了接收信号的数学分布；计算了关于接收信号的pdf和cdf，并对其进行折叠，通过折叠能看出不同QAM调制的cdf有着区别，通过最小二乘法判定cdf拟合程度达到QAM调制识别的目的。仿真结果表明，方法性能较好，尤其是在低信噪比情况下，正确识别率得到了一定的提高。本文方法的主要缺点时当样本数较少时，识别性能仍旧有待提高。