预制平行双节理类岩石材料板动态破坏试验研究

王奇智 ，夏开文 ，吴帮标 ，徐 颖 ，刘 丰

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300350；2. 天津大学建筑工程学院，天津 300350)

近年来，国家中西部地区大型基建项目飞速发展，随着工程问题研究的深入，节理裂隙的发展成为岩体力学研究热点.一方面，在基础建设领域，为防止节理岩体出现塌方、滑坡等工程事故，必须采取有效措施控制岩体的裂隙扩展；另一方面，在石油、页岩气开采等领域，则需要采用一些手段促进和控制裂隙的发展.研究和实践表明，应力扰动造成岩体原有节理裂隙面的演化、扩展和贯通，最终失稳破坏[1].

目前国内外学者相关研究主要集中在完整岩石在不同加载条件下的裂纹产生、扩展致岩石破坏，或带有预制节理的静力学试验.

Brace等[2]最早利用单轴、双轴试验机对含预制节理的岩石样品进行了静力学试验，发现了倾斜节理裂隙的翼型扩展规律，对角度等影响因素并未考虑；Wong等[3]对单一节理试件翼裂纹及次生裂纹的的扩展规律进行了研究；Bobet等[4]利用石膏所做的倾斜单裂纹压缩试验观察到了翼型裂纹和次生剪切裂纹的起裂、扩展和贯通过程，宏观描述居多，并未定量分析.国内很多学者也对节理岩体的裂隙扩展机理进行了研究，杨圣奇等[5]开展了含单一节理静态岩体力学试验，从试验角度获得了裂隙扩展机理，其以分析试样整体性参数为主，没有进一步对裂纹周边位移场、应力场进行详细描述；张伟等[6]利用模型试验研究了节理倾角对节理岩体力学特性的影响，其研究主要以静态加载为主，未考虑加载率效应.对于静态荷载下多节理岩体的裂隙扩展研究，Ashby等[7]研究了压缩应力状态下脆性固体中裂纹的生长和相互作用，并对这一系列力学行为进行了建模，提出了损伤力学理论的框架，但数值分析存在假设及选择性忽略条件，破坏结果与真实岩石破坏存在一定差距；Ramamurthy[8]基于单轴和三轴试验结果，提出了一个能考虑节理数目、节理方位和节理面强度的试验综合系数，以考虑节理剪切破坏为主；陈卫忠等[9]用试验和数值计算方法研究了翼型节理岩体在单轴、双轴荷载作用下裂隙扩展贯通的规律；张波等[10-12]使用类岩石材料，制作交叉节理，分析单轴应力状态下不同节理形态的裂隙扩展规律及静态应力场，其研究内容以填充闭合裂纹为主.

对于岩石动态断裂实验领域，张盛等[13]和 Wang等[14]使用 SHPB测试了预制节理长度与断裂韧度之间的关系.Dai等[15-17]利用SHPB对带缺口的巴西圆盘及半巴西圆盘进行了动态荷载测试，得到了加载率与其Ⅰ型断裂韧度之间的关系.Wang等[18-19]得到了中间含裂缝的大理岩的Ⅰ型和Ⅱ型动态断裂韧度.以上研究属于岩石特性试验，对节理裂隙的影响程度欠考虑.Zou等[20-21]用试验方法得到了动态荷载作用下岩石材料的裂纹起裂和扩展规律，比较了静、动荷载下节理裂隙的扩展情况，发现动态荷载作用下的强度和应变都比静态荷载作用下大，但其动态测试只考虑了某一固定加载率，还有待进一步深入研究.Gao等[22-24]使用数字图像相关(DIC)方法捕捉了岩石受载破坏时的动态位移场，得到裂纹尖端位置及应力强度因子等断裂参数，确定裂纹扩展速度、断裂韧度等，研究过程中对裂纹路扩展径进行了固定，且只考虑了Ⅰ型断裂.

综上所述，岩石裂隙扩展作为岩石力学中的一个方向，已经有了比较广泛的研究，特别是在静态荷载作用下，岩体裂隙的扩展规律研究较为成熟，而对于动载作用下岩石的力学响应机理尚存在以下问题：首先，动载条件下，研究主要集中于完整岩石的特性测量，例如岩石断裂的起裂韧度和传播韧度，而对裂纹的扩展规律的研究相对混乱，系统性较差；第二，对于含有预制裂纹的岩体的裂隙动态扩展机制讨论不多；第三，对节理岩体的裂隙尖端应力场动态扩展情况以定性现象描述为主，缺乏深入量化分析.

因此，动载下含节理岩体的破坏特性研究的必要性凸显.本试验基于断裂动力学理论，拟预制双节理类岩石材料板作为研究对象，结合SHPB动力加载系统，揭示预制张开型平行双节理岩体在动态加载条件下的破坏特性.

1 试验准备

1.1 试验方案与试样制备

试验样品采用类岩石材料水泥砂浆制备，水泥采用 725标号，参考相关建筑材料规范进行配比，水泥、水、砂质量比为 1∶0.57∶3，在试样中心位置预制贯通裂纹，浇筑成型后标准养护 28d，并进行平整度打磨达到标准尺寸 47mm×47mm×15mm，裂纹长度 6mm，厚度 0.1mm.最后表面粘贴散斑纸配合后期DIC摄像，数量为56块，共7组(倾角α为0°～90°，间隔 15°)，每组 8块.样品及加载如图 1所示.试验方案见表 1.裂缝制备采用超薄钢片黏结磨具底部，样品浇筑养护 1d后，拔出钢片即可形成预制裂缝.

图1 样品及加载示意Fig.1 Schematic diagram of specimen and loading

表1 含预制张开型双节理岩体试验方案设计Tab.1 Design of test scheme for prefabricated double cracked rock mass

加载率通过粘贴在 SHPB上的应变片电信号转化而来，静态弹性模量和泊松比通过试验测试而来.

1.2 试验设备及方法

分离式霍普金森压杆(SHPB)作为加载系统，提供 300～1200GPa/s的加载率范围(应变率 10～60s-1).试验装置位于天津大学建筑工程学院岩土所，加载系统包括动力系统、电信号采集系统和监测系统.加载率变化主要通过气室内气体压力实现，为获得应力平衡加载状态，在子弹撞击部位粘贴波形整形器得到光滑加载曲线.整套系统如图2所示.配合超高速摄像机(极限速度 500万帧/s)，捕捉试样动态破坏全过程.相邻时间图像时间步达到1μs精度.

1.3 数据监测及处理

图2 加载系统Fig.2 Loading system

三波法原理.入射杆、透射杆应变片均采用对称粘贴方式以消除弯矩产生的应变，并假设SHPB符合一维应力波状态及均质性假定.根据应变片记录的入射波εi( t )、反射波εr( t )和透射波脉冲信号εt( t)见图3，其荷载计算公式分别为

式中：E、A分别为压杆的弹性模量和横截面积；P1( t)为入射杆荷载产生的力；P2( t)为透射杆荷载产生的力，当样品达到应力平衡时，有

图 4展示了一组预制张开型双节理试样在SHPB加载下的动态应力平衡图.

图3 一维应力波原理图Fig.3 Diagram of one-dimensional stress wave principle

图4 典型的SHPB应力平衡图Fig.4 Dynamic stress balance in a typical SHPB test

2 结果分析

2.1 强度参数

从加载率角度来看，不同加载率会得到不同的应力应变曲线，曲线峰值一般代表试样的动态破坏强度.加载率越大，其应力应变曲线峰值越大.

应力-应变关系曲线反映了样品破坏的一个过程，根据图 5可以看出，一般分为 3个阶段：初始阶段为线弹性变形，第 2阶段为非线性变形，最终演化成宏观破坏.在低加载率下，非线性变形阶段较长较缓，而高加载率条件下，第 2阶段逐渐不明显，非线性过渡区域变小.样品的破坏强度主要根据应力-应变曲线峰值确定.由图 5可以看出，不同加载率节理试样应力-应变曲线峰值不尽相同，于是将不同角度不同加载率试验结果汇总对比，见图6.

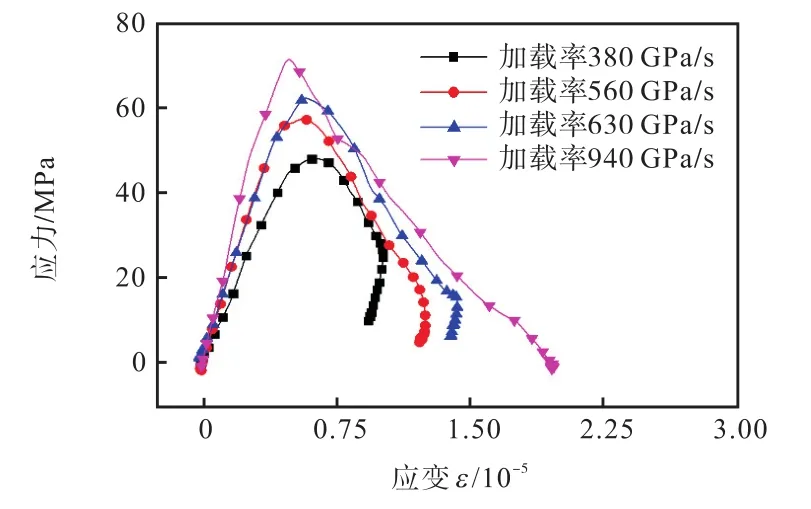
图5 双裂纹动态应力-应变曲线(α＝60°)Fig.5 Stress-strain curves of specimens containing two parallel fissures under dynamic compression(α＝60°)

图 6汇总了各角度节理试样在不同加载率下的最终动态强度，数据结果具有一定的离散性，90°与30°样品组强度较高，45°与 75°样品组强度较低，其余样品组强度居中.为了更好地发现各角度样品组强度变化规律，现将其强度与加载率进行加权平均(强度×自身加载率/各试样加载率之和)，得到图7.

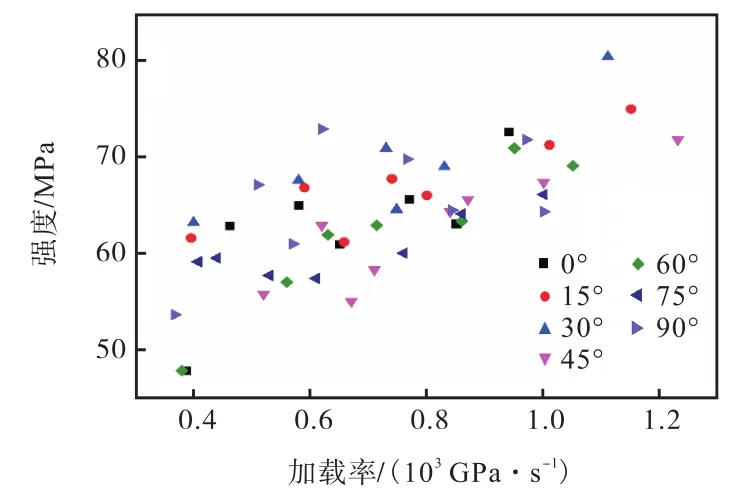
图6 各角度节理试样动态强度汇总Fig.6 Summary of dynamic strength of jointed specimens at various angles

图 7清晰地展现了强度变化规律，即 30°样品组强度最高，而 75°样品组强度最低，整体展现出倾斜的 N字形变化规律.强度最大值与最小值差值约为16%.

图7 各角度节理样品动态强度加权平均值曲线Fig.7 Weighted average dynamic strength curve of jointed specimens at various angles

2.2 破坏模式

在动态冲击过程中，使用示波器信号触发相机拍摄，调试相机拍照时间及对应的帧数，捕捉 0°～90°预制裂纹试样的破坏过程，包括裂隙的起裂、动态传播、闭合及完全破坏(见图8).

图8 预制张开型双节理30°试样破坏过程Fig.8 Dynamic damage failure diagram of 30° prefabricated opened two parallel flaws specimens

图 8为原始拍照图片，图9为 DIC技术处理后的图片，此试样加载率为 1 110 GPa/s，可以观察图8(a)发现主应变首先在两个节理之间聚集，随后主应变以 4个节理尖端为出发点，逐渐与外部裂纹连通，最后形成X 型主裂隙，图 8(b)、(c)则可观察到双节理岩桥破坏模式，裂隙为两尖端反向对称连接.

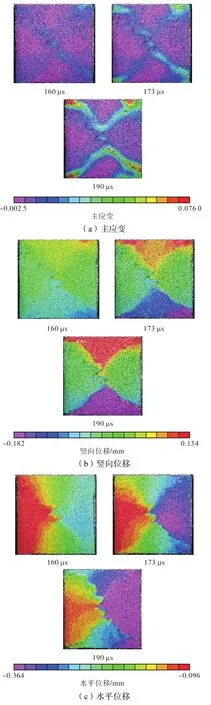
图9 预制张开型双节理30°试样破坏过程云图Fig.9 Dynamic damage failure nephogram of 30° prefabricated opened two parallel flaws specimens

图 10为 0～90°样品在动载下的(加载率 643～1230GPa/s)典型破坏模式，宏观模式均为 X型破坏，在低加载率条件下部分样品出现Y型破坏，即少一条主裂纹，但其趋势依然为X型破坏.

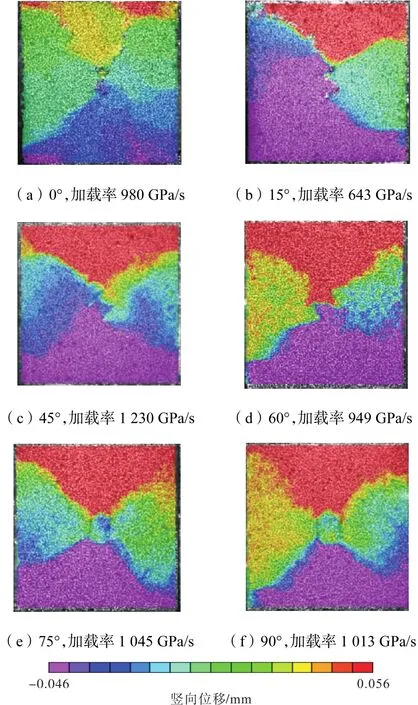
图10 预制张开型双节理试样破坏过程云图Fig.10 Dynamic damage failure nephogram of prefabricated opened two parallel flaws specimens

角度变化对破坏模式的影响主要体现在两条预制节理中间部位的岩桥破坏模式，岩桥破坏类型有两种：一种为两条节理尖端斜对角线相连的 Z型破坏，另一种为“口”字形破坏.此外，过高的加载率会改变Z型岩桥破坏的模式，具体模式及分布见图11.其中，T代表张拉破坏，S代表剪切破坏.

2.3 裂纹尖端应力场讨论

断裂动力学中，裂纹尖端动态起裂是断裂行为的重要组成部分.本节将利用数学的方法，捕捉其裂尖动态起裂峰值应力，主要方法如下：通过数字图形相关技术(DIC)捕获裂纹尖端位移场(见图 12)，代入Williams多项式，进行数据拟合得到裂纹尖端Ⅰ、Ⅱ型动态起裂时刻的峰值应力强度因子.其主要原理为假设裂纹尖端坐标和应力强度因子 K为未知数，若裂尖坐标与极坐标原点重合，且裂纹面与x轴的负半轴重合，则用极坐标 r和θ表示的裂纹尖端区域非线性位移场方程组[25]求解裂纹尖端应力场，即

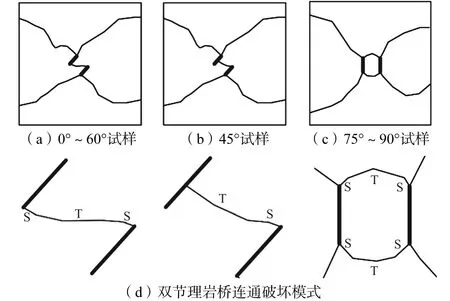
图11 岩桥破坏形态Fig.11 Schematic of rock bridge damage

图12 MATLAB位移场捕捉示意Fig.12 Displacement field capture schematic by MATLAB

式中：ux、uy代表x和y方向的位移分量；μ为切变模量，μ=E/[2(1+v)]，在平面应力问题中κ=(3-4v)/(1+v)、平面应变问题中κ=(3-4v)；E和v分别为弹性模量和泊松比；r和θ为极坐标参数；An与Bn分别为位移中对应于Ⅰ型裂纹和Ⅱ型裂纹的系数；n表示级数序列.裂纹的平动取决于系数A0和B0，而刚体转动取决于系数B2.Ⅰ型裂纹级数展开的第 2项(对应于n＝2)通常被称为T应力分量.系数A1和B1分别与Ⅰ型和Ⅱ型裂纹的应力强度因子SIFs相对应，

根据式(5)，可以得到不同时刻裂纹尖端的应力场，每个样品在不同加载率下其峰值均有不同.

下面将讨论不同类型样品在不同加载率下其裂纹尖端应力场的不同点及其变化规律.由于节理样品存在 4个裂纹尖端，根据对称原理，本文统一采集靠近加载源的两个裂尖应力场.以CA、CB区分具体尖端点，其中CA点为0～60°样品组岩桥断裂的一个尖端点，CB为另一尖端点(见图 13)，图 13(a)代表0°～60°试样组，图 13(b)代表 75°～90°试样组.

图13 预制张开型双节理尖端应力场捕捉示意Fig.13 Captured schematic of crack tip stress field at prefabricated opened two parallel flaws of specimens

裂纹尖端应力由张拉应力KⅠ和剪切应力KⅡ组成，将 DIC捕捉的位移场代入式(5)，得到不同加载率下裂纹尖端动态起裂应力场峰值.

图 14展现了 0°试样组裂纹尖端应力强度因子(SIF)随加载率的变化，两点应力场变化规律基本一致，KⅠ随加载率先上升后下降，最高点位于加载率650GPa/s附近；KⅡ同样随加载率上升而增大，在加载率 950GPa/s附近开始回落.KⅠ的变化幅度大于KⅡ.对于这种变化规律，一般认为随着加载率变大，单位时间输入的能量超过了预制节理区域的承载能力，试样在其他区域衍生了更多的微裂纹，分担了预制裂纹区域的应力场，导致其加载率超过某一点后应力场开始减弱.使用式(4)和(5)从位移场计算应力强度因子，计算为正值时表示张拉应力，负值则为压应力.力场规律较为相似，后续不再讨论 30°～90°试样组自身CA、CB点的对比.

由于 0°～60°样品组岩桥区域破坏形式一致，因此，合并分析其角度带来的影响，图 16展示了岩桥裂纹起始点CA的KⅡ随角度、加载率的变化规律，数据趋势基本分为 3组：①0°试样组，受剪较小，基本线性趋势；②15°～45°试样组，先增长后下降；③60°试样组，持续上升.

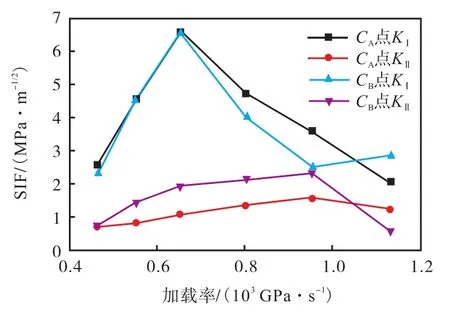
图14 预制双节理 0°试样组节理尖端应力强度因子随加载率变化Fig.14 Variation of crack tip stress intensity factor with loading rate at 0° prefabricated opened two parallel flaws specimens

0°试样组CA、CB两点的应力场幅值略有差异，CA点KⅠ略大于CB点，而KⅡ则略小于CB点，岩桥断裂连接点CA并未显著异于CB.

0°试样组的规律并未延续到其他角度，15°试样组的规律见图15.

由图 15可知，CA、CB两点KⅡ明显大于KⅠ，与0°试样组相反；其次，CA、CB两点KⅡ都是随加载率先增后减，峰值位置不同，CA点KⅡ对应的加载率要大于CB点，假设断裂阈值不变，500～600GPa/s加载率条件下，主裂纹先开裂，当加载率上升到 700～800GPa/s时，岩桥节理尖端先发生剪切破坏.

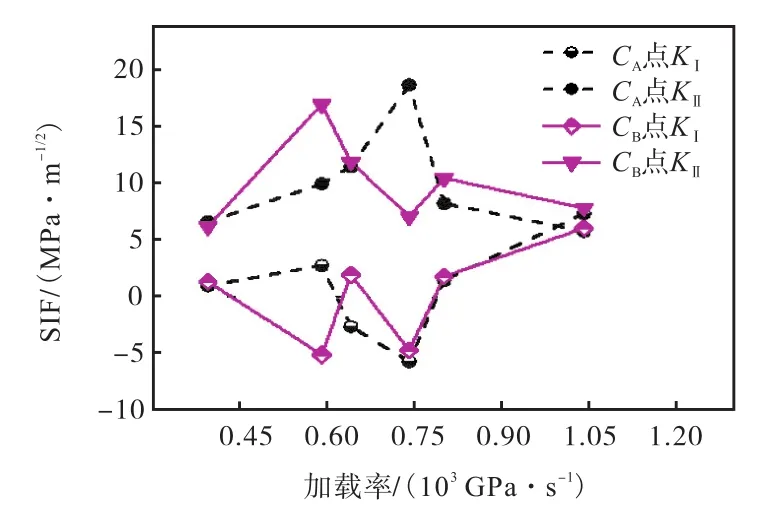
图15 预制张开型双节理 15°试样组裂纹尖端应力场随加载率变化Fig.15 Variation of stress field with loading rate at the crack tip of 15° prefabricated opened two parallel flaws specimens

最重要的一点是KⅠ出现负值，说明位移场为挤压形态，导致传统断裂力学中的KⅠ消失，在经典断裂力学理论中，裂缝宽度假设为 0，当KⅠ出现负值时，裂缝两个面会产生穿透现象，这在物理学中是不会存在的，但由于实际裂缝存在一定厚度，裂纹受压后裂缝宽度变小，会产生负的KⅠ.由图15可以看出，CA、CB两点KⅠ极小值处基本对应其KⅡ最大值，说明裂缝受压后加大了其KⅡ应力场.同一样品CA、CB两点应

图16 预制张开型双节理 0°～60°试样组裂纹尖端 CA点剪切应力场随加载率变化Fig.16 Variation of crack tip CA shear stress field with loading rate at 0°—60° prefabricated opened two parallel flaws specimens

分析其原因，0°试样组加载方向和预制裂缝平行，张拉破坏为主；15°～45°试样组受剪为主，KⅡ先随加载率上升而增大，后加载率达到一定程度后衰减，主要原因为高加载率使岩桥破坏形态发生改变(见图 11)，导致预制裂纹尖端应力场变小；60°试样组中，剪应力随加载率的变大而持续上升，其原因为角度过大导致压剪破坏，受压产生的摩擦力占据了主导地位，图17可以清晰地解释这一点.图17的拉压应力场表现为 60°试样组受压最大，0°试样组受拉，其他角度试样居中，与图 15基本上能够形成对应关系，即受压程度越大，剪切应力场越强.

图18为CB点的剪切应力场，与CA点的剪切应力场相似度较高，同样为 0°最小，60°最大，15°～45°居中，数据线性程度较高.图19为CB点的拉压应力场，其形态与CA点也颇为相似，区别依然为 15°～45°试样分布较为集中.说明岩桥区域破坏对CA点应力场规律有一定的影响，但影响较小.

图20和图21分别为75°和90°倾角预制双裂纹试样组尖端应力场，两者规律类似，压应力较大，KⅡ较小，其中 75°样品组由于不完全垂直加载方向，其KⅡ略有起伏，CA、CB点数值也非常接近，90°试样组KⅡ值因为垂直加载方向起伏非常小.两组试样CA、CB两点自身对比受压变化规律也较为一致.

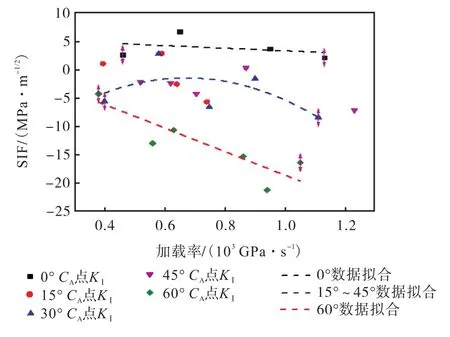
图17 预制张开型双节理 0°～60°试样组裂纹尖端 CA点拉压应力场随加载率变化Fig.17 Variation of crack tip CA tensile and compressive stress field with loading rate at 0°—60° prefabriated opened two parallel flaws specimen

图18 预制张开型双节理 0°～60°试样组裂纹尖端 CB点剪切应力场随加载率变化Fig.18 Variation of crack tip CB shear stress field with loading rate at 0°—60° prefabricated opened two parallel flaws specimens

图19 预制张开型双节理 0°～60°试样组裂纹尖端 CB点拉压应力场随加载率变化Fig.19 Variation of crack tip CB tensile and compressive stress field with loading rate at 0°—60° prefabriated opened two parallel flaws specimen

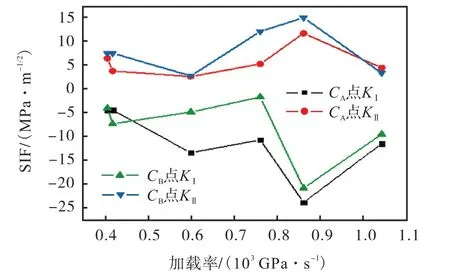
图20 预制张开型双节理75°倾角试样组裂纹尖端CA、CB点应力场随加载率变化Fig.20 Variation of stress field with loading rate at the crack tip CA and CB points of 75° prefabricated opened two parallel flaws specimens

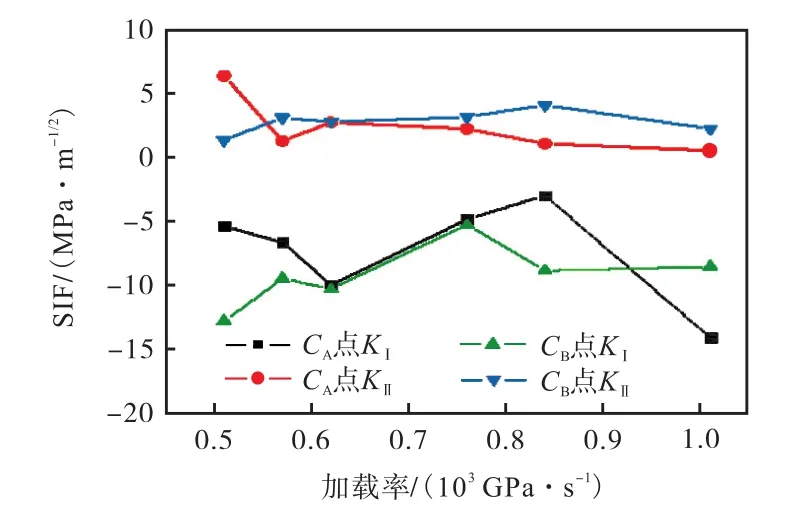
图21 预制张开型双节理90°倾角试样组裂纹尖端CA、CB点应力场随加载率变化Fig.21 Variation of stress field with loading rate at the crack tip CA and CB points of 90° prefabricated opened two parallel flaws specimens

3 结 论

本文借助SHPB加载系统，结合超高速摄像机和DIC技术，对平行双节理岩石类(水泥砂浆)样品进行动态压缩试验，主要结论如下.

(1) 30°样品组强度最高，此现象与单裂纹试样强度规律一致，而 75°样品组强度最低，整体展现出倾斜的N字形变化规律.

(2) 多角度平行双裂纹试样基本呈现 X类型破坏，试样中心部位因为有预制节理裂隙存在，两者中间部位会出现应变集中，岩桥会连通破坏.岩桥破坏类型主要有两种：一种为两条节理尖端斜对角线相连的 Z型破坏；另一种为口字形破坏.此外，过高的加载率会改变Z型岩桥破坏的模式.

(3) 对于破坏模式类似的 0°～60°试样组，0°裂纹尖端应力场较小，15°～45°略高，60°试样组则由于角度原因，受压明显导致摩擦力剧增，使得KⅡ持续增长.75°～90°样品组应力场由于相对加载方向垂直度较高，导致KⅡ相对较小，变化幅度也较小，最后两组的破坏形态也基本对称，不同裂纹尖端的KⅡ差值也较小.

(4) 岩桥破坏点CA应力场变化规律与非岩桥点CB略有不同，主要体现在高加载率时，岩桥破坏模式产生变化导致CA衰减，整体表现出类抛物线走势；CB应力场则随加载率逐渐增长呈现出线性规律.

(5) 类推本文结论，在岩石工程中，动载会导致结构面区域产生裂纹集中，并向外发散，原有的结构面也会互相贯通，进一步弱化裂纹发展核心区；材料胶结形式与水泥砂浆类似的砂岩，其结构面与加载方向夹角若不同，则可能会产生约 16%的强度差；线性增长的加载率可以逐渐加强结构面应力场使其更加容易破裂，但是过高的加载率改变了结构面之间的连通破坏形式，因此，针对不同的破岩目的，可以对动态加载方式做一些选择.