基于Pareto解集的多目标农业水土资源优化配置模型

郭 萍，单宝英，郭珊珊

(中国农业大学水利与土木工程学院，北京 100083)

进行干旱缺水地区农业水土资源多目标优化配 置的研究，对于保障地区经济可持续发展、资源可持续利用具有重要意义.传统的关于农业水土资源优化配置的相关研究大多是将水资源与土地资源两者分开配置[1]：一种是“以土定水”，在种植结构一定的情况下对灌溉水资源进行优化配置[1-2]；另一种是在灌溉制度已知的情况下对种植结构进行优化[3-4].但是水资源与土地资源作为农业系统的两个子系统，仅配置一方未能体现出二者相互制约、相互影响的关系[5].同时，水土资源规划利用涉及到的管理目标常常不只一种，通常需要兼顾经济发展、资源利用等多个目标，实现地区可持续发展.多目标规划模型因其对实际问题的良好解释在水资源和土地资源优化配置中得到广泛研究[6].但是常见的农业水土资源MOP求解方法(如权重系数法、理想点法、主要目标法等)大多是先对目标赋权，将多目标规划转换成为单目标规划，再进行求解[7-8].目标权重的细微变化可能会对优化结果产生很大的影响，而对于现实生活中目标之间存在博弈的多目标优化问题，精确的决策偏好信息大多难以获得而且并非一成不变；并且，农业水土资源 MOP问题中的多个优化目标往往是互相矛盾且不可公度的[9]，目标之间存在制衡和博弈.若此时将多目标规划转换为单目标规划，会造成大量信息丢失，不利于探究目标间的博弈过程.因此，将多目标优化问题转换成单目标再进行求解的方法虽然简便，但适用性有限.

基于以上问题，本研究将水资源与土地资源作为相互联系的子系统，构建非线性多目标水土资源优化配置模型，尝试解决缺水灌区水土资源联合配置问题.针对传统 MOP模型求解方法引起的信息丢失问题，采用多目标遗传算法求解模型的 Pareto解集(不被可行解集中的任何解支配的解称为 Pareto解或非劣解；由所有非劣解组成的集合称为多目标优化问题的最优解集，即Pareto解集[9])，以期为地区水资源管理部门提供更丰富的决策信息和更有价值的决策支持.

1 模型建立

1.1 决策变量

本模型旨在对灌区水土资源进行优化配置，决策变量包括：①不同作物生育阶段内地表水和地下水资源逐月配置量；②灌区作物种植结构.

1.2 目标函数

1) 灌区灌溉净效益目标

灌溉净效益目标反映了农业灌溉水资源对灌区经济发展的贡献情况.不同的种植结构和灌溉水量直接影响作物产量从而影响当地农民收入状况.在对水土资源进行优化配置时，灌区灌溉净效益是衡量农业种植收益的重要指导目标.按能否获得水分生产函数将灌区内作物分为两类，并采用不同的净效益表征方法.将作物分为两类：对于能够获取到水分生产函数的作物，记为第一类作物，使用二次水分生产函数表征作物产量与灌溉水量的关系，乘以作物价格得到其毛灌溉收益，再用毛灌溉效益减去作物生产成本从而得到净灌溉效益，其中作物生产成本包括种植成本、水费等；对于难以获取水分生产函数的作物，记为第二类作物，使用单方水效益表征灌溉水量与灌溉净效益之间关系.灌区总的灌溉净效益为第一类作物与第二类作物的灌溉净效益之和，优化模型的第一个目标为总灌溉净效益最大，具体表示为

式中第一类作物毛灌溉效益Bc、生产成本Cc和第二类作物灌溉净效益Ne表达式分别为

其中作物全生育期二次水分生产函数iY表示为

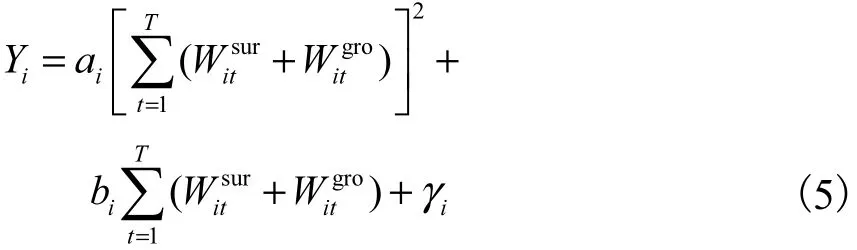
2) 灌区单方水灌溉效益目标

对于水资源短缺的地区，合理高效地利用农业水资源对社会、生态等的可持续发展具有重要意义.因此在对灌区水土资源进行优化配置时，灌区水资源管理部门不仅会追求总灌溉净效益最大，而且要保证当地水资源利用效率(即利用单位水量可以获得的收益)尽可能大.使用单方水效益来表征灌区水资源利用效率，具体为

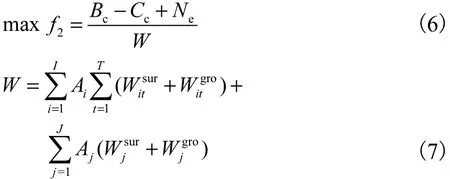
1.3 约束条件

1) 地表水可利用水量约束

灌区所有作物逐月总的地表水灌溉水量应不超过有效的地表水可利用水量.对于引水灌区，有效的地表水可利用水量应扣除渠系输水和田间灌溉过程中渗漏损失，具体表示为

2) 作物需水量、灌溉水量约束

为保证作物生长状况，对于实验数据丰富的第一类作物，逐月耗水量应大于最小需水量.在此将作物耗水量简化为地表水、地下水灌水量与有效降雨量之和.最小需水量可以由作物腾发量乘以小于 1的系数确定；对于第二类作物，可以根据实际生产经验对其总灌水量施加约束.

3) 地表水、地下水转换约束

根据水量平衡原理，在灌区中，补给的地下水资源主要来自渠系及田间入渗补给、降雨入渗补给、地下含水层补给等，地表水、地下水转换关系[10]如图 1所示.为保护地下水资源，在利用地下水资源进行灌溉时，开采的地下水量应不超过补给量，保证灌区地下水量采补平衡.表达式[11]为

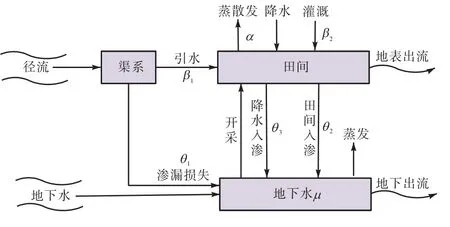
图1 地表水、地下水转换关系Fig.1 Transformation relations between surface water and groundwater

1.4 模型求解

遗传算法作为一种应用较广的群体智能进化算法，具有强大的全局寻优能力[12].多目标遗传算法(multi-objective genetic algorithm，MOGA)的内在运行机制与全局寻优特性[12]与多目标优化问题求解相契合，随着向量评估遗传算法(VEGA)[13]、非支配排序遗传算法(NSGA)[14]、带精英策略的非支配排序遗传算法(NSGA-Ⅱ)[15]等方法的相继提出，遗传算法在求解多目标优化问题的 Pareto解(非劣解)方面迅速得到广泛应用[16-17].本研究采用带精英策略的并列选择法[18]进行求解，算法具体实现步骤见图2.

图2 MOGA算法流程Fig.2 Flow chart of MOGA

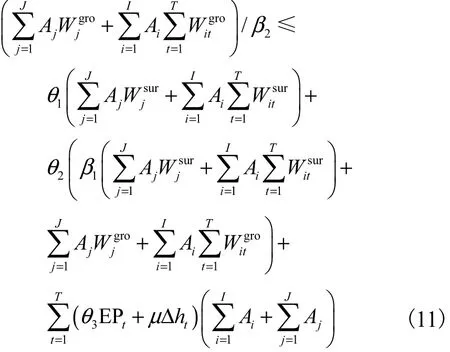
4) 土地资源约束

为保证当地粮食安全和种植结构平衡，给予最大最小种植面积约束.

5) 非负约束

本模型变量较多且约束复杂，使用可行解变换法[18]处理约束条件.在生成初始种群、选择、交叉、变异等每步算子结束后验证个体是否在可行域内，保证整个寻优过程在可行域内进行.对于不同类型或不同数量级的变量，在进行初始种群产生、变异操作时应该分开进行.

循环寻优算法若干次，直至Pareto前沿面稳定.

2 实例应用

2.1 研究区域

本研究以黑河中游的盈科灌区作为实例应用区域.黑河是我国第二大内陆河，黑河中游作为河西走廊绿洲消耗区[19]，集中了全流域 95%的耕地，消耗黑河干流 70%的水量[11].而随着一系列黑河分水调水方案的实施，黑河中游农业水资源可利用量正逐渐减少.对黑河中游农业水土资源进行优化配置，对保证中游地区的经济发展、社会稳定、粮食安全和下游地区生态环境健康具有重要意义.盈科灌区位于黑河流域中游张掖绿洲冲洪积细土平原上，是绿洲核心灌区的典型代表[20].盈科灌区多年平均降雨量127.4mm，多年平均蒸发量约1400～2900mm，蒸发量远大于降水量，降水量远远不能满足作物需水要求[21]，灌区农业发展严重依赖于灌溉.盈科灌区主要种植作物包括玉米(大田玉米、制种玉米)、小麦、蔬菜等，其中大田玉米和小麦为粮食作物，制种玉米和蔬菜为经济作物.

2.2 数据来源

大田玉米、制种玉米和小麦根据相关田间试验，可获得其水分生产函数，记为第一类作物；蔬菜种植庞杂，种类繁多，将灌溉水量与经济效益的关系使用单方水效益(单位毛灌水所产生的经济效益)进行简化[19]，即蔬菜记为第二类作物.盈科灌区作物生育期集中在 4—9月，对每个月的地表水、地下水量进行配置.灌区总可种植面积 13424hm2，蔬菜单方水效益为 4.16元/kg，最小田间灌溉量为 500mm，最大田间灌溉量为 800mm[19].地表水水价为 0.169元/m3，地下水水价为 0.880元/m3[19].其中作物最小需水量由作物腾发量乘以折减系数 0.7确定，作物腾发量由参考作物腾发量乘以作物系数 kc求得[11].模型所需的作物成本效益数据[19]、水转换相关系数[10]、现状灌溉定额[11]、水分生产函数[11]、可利用水资源量数据[11]等参照已有研究，见表1～表4.

表1 作物相关系数Tab.1 Basic parameters for different crops

表2 灌区逐月地表水可用水量及有效降雨量Tab.2 Monthly surface water availability and effective rainfall

表4 地表水、地下水转换中相关系数Tab.4 Correlation coefficients of surface water and ground water

表3 作物最小需水量Tab.3 for crops

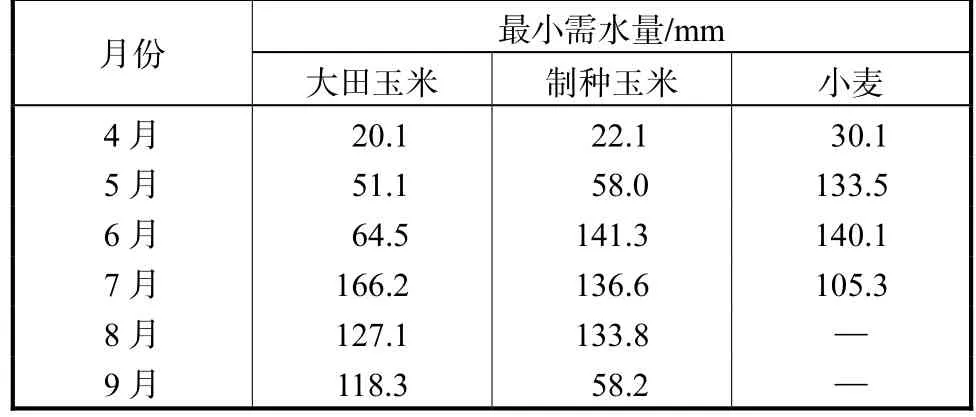
表3 作物最小需水量Tab.3 for crops

月份 大田玉米 制种玉米 小麦最小需水量/mm 4月 020.1 022.1 030.1 5月 051.1 058.0 133.5 6月 064.5 141.3 140.1 7月 166.2 136.6 105.3 8月 127.1 133.8 —9月 118.3 058.2 —

2.3 结果与分析

将该水土资源优化配置模型应用于盈科灌区，使用MATLAB编写多目标遗传算法程序求解该非线性多目标水土资源优化配置模型，共求得194组非劣的水土资源优化配置方案.

2.3.1 Pareto解集

求解得到的 Pareto前沿面见图 3.为方便表示，沿总效益递减方向对 Pareto前沿面上的非劣配置方案进行编号，总效益最大但单方水效益最小的配置方案为第1号方案，总效益最小但单方水效益最大的配置方案为第194号方案.

图3 Pareto前沿面Fig.3 Pareto frontier

灌区总效益和单方水效益两个目标均为越大越优.在 Pareto前沿面上，非劣的水土资源优化配置方案的一个目标值增大必然会引起另一个目标的减小，从第1号方案至194号方案，模型优化结果从倾向于总效益最大逐步过渡到单方水效益最大，灌溉单方水效益从 3.51元/m3增至 4.29元/m3，而灌区灌溉净效益从3.31×108元下降至3.08×108元，不存在某一种方案使得优化的两个目标值同时达到最大，两个目标之间存在博弈.现状灌溉定额及种植结构下，盈科灌区灌溉总效益为 2.97×108元，单方水效益为 3.84元/m3，模型通过协同优化灌溉制度与种植结构，优化后灌区灌溉总效益较现状增加 4.2%～10.3%，优化效果显著.

Pareto前沿面上的点即为多目标优化问题的最优解集.传统的将多目标转化成单目标再进行求解的方法，只能得到 Pareto前沿面上的一个点，目标之间丰富的博弈信息被忽略.求解出整个 Pareto最优解集，不仅可以展现出目标之间的博弈关系、提供更多决策支持信息，而且无需事先确定各个目标的权重，大量的非劣配置方案可以为决策过程提供更多选择，满足不同决策制定者的不同偏好需要.当决策偏好发生变化时，无需重新计算，在 Pareto解集中重新选择即可.

2.3.2 水资源优化结果

194组非劣配置方案的每种作物全生育期配水结果见图 4.从图 4中可以看出，随着编号增加，大田玉米、制种玉米、小麦 3种作物的单位面积全生育期配水量逐渐减小.这是因为作物配水量对灌溉效益和水资源利用效率有着直接作用.模型是基于二次水分生产函数衡量第一类作物灌水量与产量之间的关系，在一定范围内，随着配水量的增加，大田玉米、制种玉米、小麦产量增加，其单位面积上的灌溉净收益不断增加(见图 5)：大田玉米单位面积灌溉净效益从 18357元/hm2增加至 21349元/hm2，制种玉米单位面积灌溉净效益从 23152元/hm2增加至25407元/hm2，小麦单位面积灌溉净效益从11852元/hm2增加至 13200元/hm2.因此当模型倾向于追求总的灌溉净效益最大时，作物配水量会向灌水上限靠近.

图4 非劣方案集作物配水量Fig.4 Non-inferior program set crop water distribution

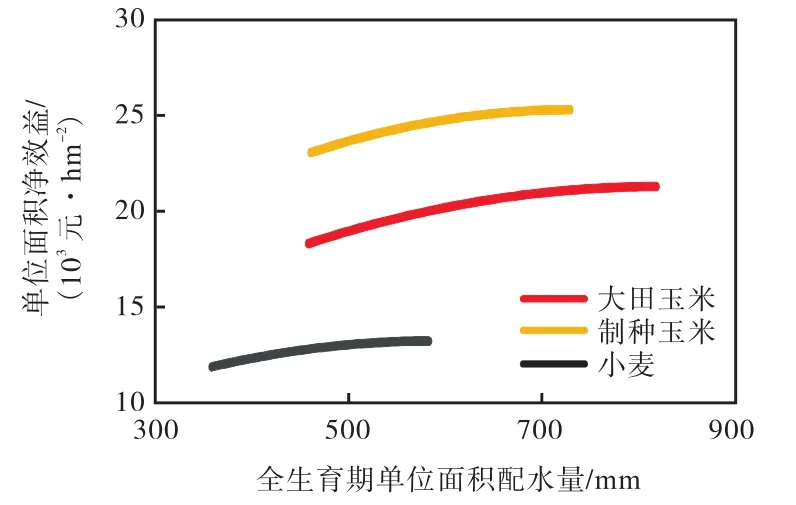
图5 作物配水与净效益关系曲线Fig.5 Crop water distribution and net benefit curve

同样基于二次水分生产函数，随着单位面积配水量增加，水分生产力逐渐减小.大田玉米、制种玉米和小麦 3种作物单方水灌溉效益均随灌水增加呈下降趋势(见图 6)：大田玉米单方水效益从 4.0元/m3下降至 2.6元/m3，制种玉米单方水效益从 5.0元/m3下降至 3.5元/m3，小麦单方水效益从 3.3元/m3下降至2.3元/m3.模型若想获得较大的单方水效益，必定会减少作物单位面积配水量，以提高灌水效率.所以当决策偏好从总灌水净效益最大过渡到单方水效益最大，作物单位面积配水量呈减少趋势.

由于采用固定的单方水效益来衡量蔬菜灌水与效益关系，蔬菜配水量在所有非劣方案中都处于灌水上限附近.

为具体分析生育期内逐个月份地表水、地下水配置情况，选取第 1、97、194号方案为代表方案进行分析.3组方案分别代表经济效益最大、两个目标均处于中间水平和单方水效益最大时的最优解.盈科灌区逐月地表水、地下水配置结果见图 7.图中：1_SW表示第1号方案的地表水配置水量，1_GW表示第1号方案的地下水配置水量，其余图例同理；β1β2Qt表示可利用的地表水量.3组方案在 4、5、6月份地下水灌溉量在总灌溉水量中占比区间分别为[60.1，67.6]、[47.5，52.5]、[30.4，36.6]，已经接近或超过总灌水量的 1/2.对于水资源较为紧缺、地表水可供水量较少的 4—6月份，仅靠地表水进行灌溉不能满足作物正常生长需要.这时在保证地下水资源采补平衡的前提下，考虑地表水、地下水之间转换关系对地表水、地下水进行联合配置，可以充分利用灌区渠系输配水、田间灌溉等过程中渗漏的水量，适当开采地下水进行灌溉对灌区作物前期生长具有重要作用.

图6 作物配水与水利用效率关系曲线Fig.6 Crop water distribution and water use efficiency curves

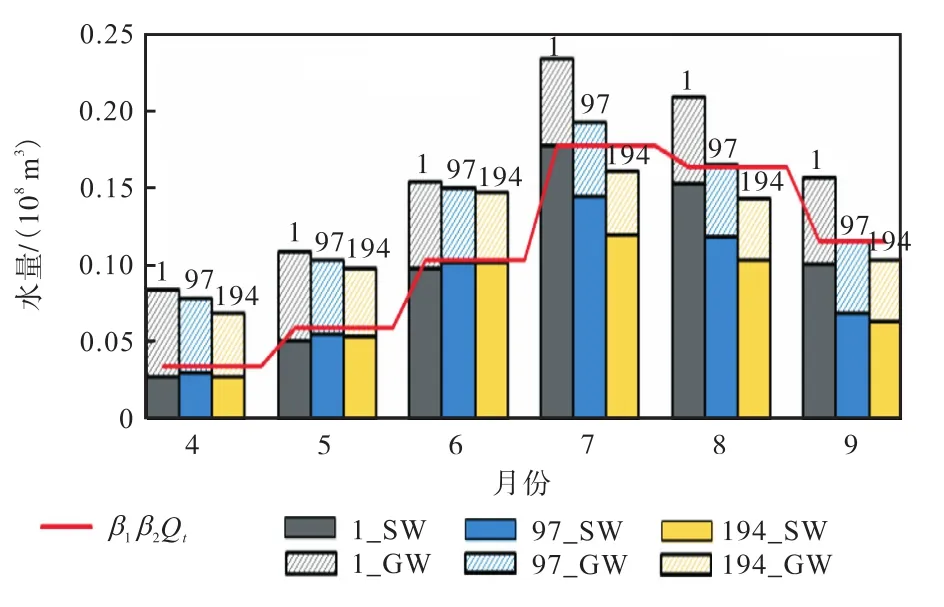
图7 第1、97、194号方案逐月地表水、地下水配置情况Fig.7 Surface water and ground water distribution by months 1，97, and 194

2.3.3 种植结构优化结果

194组非劣配置方案的每种作物配置面积见图8.图中：C1、C2、C3、C4分别表示大田玉米、制种玉米、小麦、蔬菜；C1 min表示大田玉米的最小种植面积，C1 max表示大田玉米最大种植面积，其余同理.优化前后作物种植面积及粮经比(粮食作物与经济作物种植面积比)如表 5所示.具体来看：无论是追求总效益最大目标还是单方水效益最大目标，作为粮食作物的大田玉米和小麦在面积配置上均不占优势：大田玉米和小麦的配置面积始终靠近其配置下限(见图 8(a))，优化后两种作物总种植面积仅占灌区总灌溉面积的 30%左右.这是因为受到作物市场价格的影响，粮食作物单价较低，当灌溉水量相同时，大田玉米和小麦的单位面积净收益远小于制种玉米(见图 5).在对有限的可利用灌溉面积进行分配时，粮食作物处于劣势，模型倾向于降低小麦、大田玉米的种植面积，保证经济作物(制种玉米和蔬菜)种植面积处于较高水平，以获得更大的总收益或者在获得相同单方水效益的同时得到更高的总效益.

优化前灌区粮经比为 0.582，优化后粮经比为0.295～0.307.由模型优化结果可得，适当增加高产值的经济作物的种植面积，是实现灌区平稳增收增效、提高农民收入和改善生活水平的一个重要途径.

制种玉米和蔬菜均属于收益较高的经济作物，二者相对于粮食作物在土地资源配置中处于优势地位，优化后制种玉米的种植面积较现状减少 4.6%～22.0%，但仍处于较高水平，蔬菜种植面积较现状增加 103.0%～158.0%，两种作物总种植面积占到灌区总灌溉面积的 70%左右.但是不同于大田玉米和小麦在194组配置方案中配置面积始终趋于定值，随方案编号增加，制种玉米配置面积呈增加趋势，蔬菜配置面积呈减少趋势(见图 8(b)).产生这种现象的原因是：二者水量-水资源利用效率的关系会影响到种植面积分配.蔬菜单方水效益设为定值，当配置水量较少时，制种玉米的单方水效益高于蔬菜；而随着配置水量的增加，制种玉米的单方水效益逐渐降低.当单位面积配置水量超过598mm时，制种玉米的单方水效益小于蔬菜(见图 6).对于倾向于追求总效益最大的方案(即编号数值较小的方案)，作物单位面积配水量较多，接近其灌水上限，此时蔬菜的单方水效益大于制种玉米，在满足总配水量小于可供水量的前提下，模型保证蔬菜的配置面积达到最大，在水量、配置面积的双重作用下使得灌区总的净效益达到最大.而当决策偏好逐步过渡到追求单方水效益最大时，作物单位面积配水量减少，制种玉米的单方水效益逐渐超过蔬菜，制种玉米的配置面积也逐渐增加，反超蔬菜.

2.3.4 博弈过程

使用遗传算法求解出的多目标优化问题的Pareto解集，可以清晰地展示出目标之间、作物之间、水土资源之间的博弈过程.

图8 非劣方案集作物配置面积Fig.8 Non-inferior program set crop allocation area

表5 优化前后作物种植面积Tab.5 Crop planting areas before and after optimization

将水资源与土地资源同时进行优化配置，优化结果可以展现出在生产实践中何种资源更为紧缺.在本实例应用中，当决策偏好倾向于追求总效益最大时，水资源与土地资源均为配置量越大目标越优.而此时作物对水土资源的竞争情况并不相同：对于水资源，大田玉米、制种玉米、小麦和蔬菜 4种作物的单位面积配水量皆接近灌水上限，水资源总量充足；而对于土地资源，4种作物的总配置面积十分接近灌区总种植面积，制种玉米和蔬菜的配置面积处于较高水平，大田玉米和小麦的配置面积接近最低种植面积，可以看出，在本实例应用中，相较于水资源作物对土地资源的竞争更为激烈.

在多目标优化模型中，作物对优化目标值的贡献程度会随着目标倾向性的改变而改变.当追求总效益最大时，即保障经济效益最大，单方水生产力尽可能最优(该结果对应本文Pareto遗传算法结果中的第1号方案)，大田玉米、制种玉米、小麦和蔬菜贡献的净效益分别占灌区总灌溉净效益的 14.52%、36.08%、2.25%和 47.15%，蔬菜对总灌溉净效益的贡献最大，玉米和小麦尤其是小麦对总效益的贡献很少；而当追求单方水效益最大时(对应 Pareto解集的第 194号方案)，大田玉米、制种玉米、小麦、蔬菜贡献的单方水效益分别是 4种作物平均单方水效益的0.87、1.11、0.69、0.97倍，制种玉米对单方水效益贡献高于其他3种作物.

综上所述，使用遗传算法求解出的多目标优化问题的 Pareto解集可以清晰地展示出目标之间、作物之间、水土资源之间的博弈过程，有助于决策制定者理解模型内在的运行机制，为其提供更有价值的决策支持信息.具体选择 Pareto前沿面上哪一组水土资源配置方案，需要当地管理部门根据灌区实际情况、政策要求、发展规划等统筹确定.

3 结 论

本研究构建了一种以灌溉净效益和用水效率最大为目标的地表水资源、地下水资源、作物种植结构联合优化配置模型，并将此模型应用于黑河流域中游盈科灌区，结论如下.

(1) 在保证地下水采补平衡的前提下，适当开采地下水进行灌溉，为灌区在季节性缺水阶段补充灌溉具有重要作用.

(2) 在盈科灌区，当追求总效益最大时，作物重要性从大到小依次为：蔬菜、制种玉米、大田玉米、小麦；当追求单方水效益最大时，作物重要性从大到小依次为：制种玉米、蔬菜、大田玉米、小麦.

(3) Pareto解集可以展现出多目标优化问题更多博弈信息，相较于权重系数法等只求解得到一组妥协解的方法，非劣解集更具通用性.

本文多目标农业水土优化模型是一个带有复杂约束的非线性模型，尽管使用 MOGA求解可以得到满意的 Pareto前沿面，但是模型求解过程复杂、求解速度较慢，缺乏更通用的求解程序.此外，在生产实践中，作物价格、降水量、可供水量等值存在较大的不确定性，使用均值代替具有一定局限性，后续工作应该将现实中出现的水文要素和管理要素不确定性考虑到本文提出的基于 Pareto解集的多目标农业水土资源优化模型中来.

符号说明：

sur—第 i种作物第 t月份地表水灌溉水量，mm；—第i种作物第t月份地下水灌溉水量，mm；—第j种作物地表水灌溉水量，mm；—第j种作物地下水灌溉水量，mm；—第j种作物逐月地表水灌溉水量，mm；

Ai—第i种作物种植面积，hm2；

Aj—第j种作物种植面积，hm2；

f1—灌区灌溉净效益目标，元；

Bc—第一类作物毛灌溉效益，元；

Cc—第一类作物生产成本，元；

Ne—第二类作物灌溉净效益，元；

Pi—第i种作物市场价格，元/kg；

Yi—第i种作物单位面积产量，kg/hm2；

Cpi—第i种作物种植成本，元/kg；

Cas—地表水价格，元/m3；

Cag—地下水价格，元/m3；

Vj—第j种作物单方水效益，元/m3；

ai, bi, ci—第i种作物二次水分生产函数的二次、一次、常数项系数；

f2—灌区单方水灌溉净效益目标，元/m3；

W—灌区总灌溉用水量，m3；

β1—渠系水利用系数；

β2—田间水利用系数；

Qt—第t月份地表水可利用水量，m3；

EPt—第t月份有效降雨量，mm；—第i种作物第t月份的最小需水量，mm；—蔬菜最小、最大田间总灌溉量，mm；—渠系渗漏损失系数、田间水入渗系数、降雨入渗补给系数；

Δ ht—第t月份的地下水位差，mm；

μ—地下水含水层给水度；—第i种作物最小种植面积，hm；—蔬菜最小种植面积，hm2；—灌区总的可种植面积，hm2.2

下标

i—第一类作物种类，i＝1，2，…，I；

t—作物生育期，t＝1，2，…，T；

j—第二类作物种类，j＝1，2，…，J.

上标

sur—地表水；

gro—地下水；

max—极大值；min—极小值.