Halin图上求解最大切割问题的高效算法
许莉,娄定俊,蒋一帆,秦宗蓉
(中山大学数据科学与计算机学院,广东 广州 510006)
Halin图是由德国数学家Halin提出的极小3连通平面图。给定一棵树T,其内部结点度数至少为3,即树中无度数为2的结点。将T嵌入到一个平面中,然后添加一些依次连接T的叶结点的边来组成一个圈C,同时使得添加边后的图仍然是平面图。由此得到的G=T∪C即为Halin图,其中T称为G的特征树,C为G的伴随圈。以下将G的特征树T的叶结点简称为G的叶结点。轮是一种特殊的Halin图,其特征树的内部结点只有一个,如图1所示。
由Halin图的定义可知,Halin图G有如下性质:
(i)G的所有叶结点的度为3。
(ii)G的任意两个内部面至多有1条公共边,并且每个内面与外部面恰有1条公共边。
假设T至少有两个非叶子结点,w是树T中任意一个非叶子结点,而且仅与T中一个非叶子结点相邻。不妨令与w相邻的叶子结点集合为C(w),这些结点在圈C上是一段连续的结点。我们将导出子图F=G[{w}∪C(w)]称为一个扇(fan),w为扇的中心,如图1(a)虚线中的子图,其中v5为扇的中心。
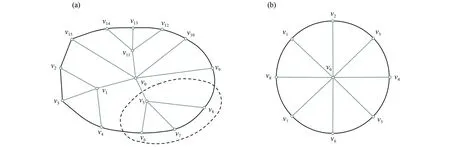
图1 Halin图中的扇和轮Fig.1 Fans of a Halin graph and a wheel
Halin图可以作为具有低成本和容错性的网络模型,常用于研究普通图中的NP完全问题。David Eppstein提出了Halin图的判定方法,Halin图可以经过一系列约化规则收缩直至K4图,同时分解为伴随圈和特征树[1]。Cornuejols等[2]在带权Halin图上提出了一个解决TSP问题的线性时间算法;Lou[3]证明每个Halin图是哈密顿连通的;Li等[4]提出了在带权Halin图的每一对顶点之间找一个最小权值的哈密顿路径的线性时间算法;Lou和Liu[5]给出了在线性时间解决Halin图的3正则子图问题的算法;Lou等[6]还给出了求解Halin图中最大线子图问题的线性时间算法。这些问题都是普通图中的NPC问题。
本文要研究的就是一个在普通图上的NPC问题:最大切割问题。最大切割问题(max-cut problem)是一类特殊的图划分问题(partitioning problem),普通图划分是指对给定的(加权的)无向图的节点集合进行划分,使得两个节点集合之间的连接数量(加权之和)最小化[7]。当各边的权为1时,此问题转化为:求G的一种切割方法,使得作为边割的边数最多。该问题在普通图上仍是NPC问题[8],接下来本文将在Halin图上,求各边权为1时的最大切割问题的一个解。
一般图的最大匹配算法(Edmonds’s matching algorithm)以Berge定理为基础,基于图的内部结点采用广度优先搜索增广路。而本文将提出的算法基于Halin图的内部面进行,对组成扇的内部面进行收缩和展开且根据一定的规则进行标记,最终得到面与面的匹配,从面的匹配结果进一步得到最大边数的割集。
下面,我们对本文所引入的术语进行定义:
设G=T∪C是一个Halin图,除了伴随圈围出的外部面外(该面我们不讨论),以围起一个面的圈是奇圈还是偶圈为标准,将Halin图的内部面分为奇面(odd)和偶面(even),例如:图2中面F1=v0v1v4v6v5v0是一个奇面,而面F1=v0v10v12v11v0一个偶面。随着Halin图中扇的收缩,各面是奇(偶)面均指它在原始Halin图G中是奇(偶)面,不因扇的收缩而改变。
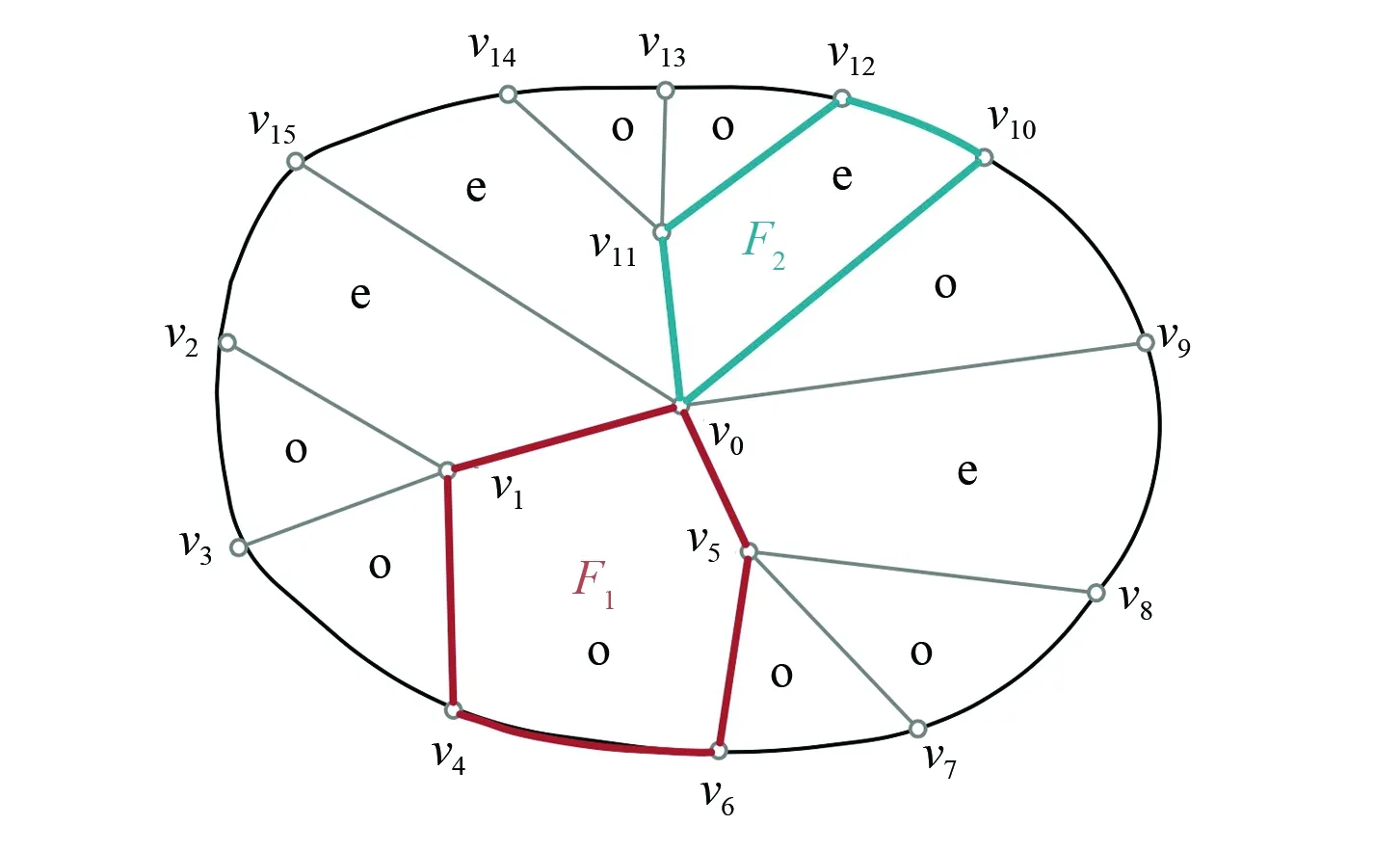
图2 Halin图的奇偶面Fig.2 Odd and even faces of Halin graph
本文提出的最大切割算法基于扇的收缩和展开,因此我们针对Halin图的扇提出“可扩”的概念,如图3所示。在扇中只有一段连续奇面情况下,如果奇面个数为2n(n≥1),则这些奇面可以进行完全的奇面对匹配,不存在未配对奇面的情况,我们将这种情况标记成为“不可扩”,即不需要将扇中奇面与扇外的奇面进行配对,如图3:①(其中两奇面之间的横线表示这两个奇面配对);如果奇面个数为2n+1(n≥0),则可以从第1个奇面开始进行配对,此时第2n+1个奇面没有被配对,定义该扇为“右可扩”,即该扇右端奇面可以与扇右侧的奇面进行配对,如图3:②。若从第2个奇面开始进行配对,则该扇可以定义为“左可扩”,如图3:③;又因为该扇既可以为“左可扩”又为“右可扩”,所以将该扇标记为“左可扩或右可扩”,如图3:④;对于可能存在偶面的含收缩扇的扇,若扇中左右两端存在两个连续的奇面串,奇面串中奇面个数都为奇数,且扇中存在偶面使左右两端的奇面串不连接,则将该扇定义为“左可扩且右可扩”,如图3:⑤;若只有右端奇面个数为奇数,则标记为“右可扩”,如图3:⑥;若只有左端奇面个数为奇数,则为“左可扩”,如图3:⑦;若两端奇面个数都为偶数,则标记为“不可扩”。

图3 定义“可扩属性”的几种情形Fig.3 The definition of “extendible” fans
将Halin图G的特征树T上的边称为内部边,伴随圈C上的边称为外部边。
将一个扇的可扩属性进行定义之后,可以将该扇收缩为外圈上一个叶结点,称为“收缩扇”,该叶结点称为“收缩扇”的伪点,如图4。Cornuejols,Naddef和Pulleyblank[3]给出了收缩扇的步骤。

图4 用“伪点”代表收缩扇Fig.4 Using a pseudo-vertex to represent a “shrink fan”
在将V划分为V1和V2之后,把一个端点在V1中,一个端点在V2中的边称为“满足条件的边”,其余的边称为“不满足条件的边”。
将G的特征树T的叶结点和内部结点在G中对应的点分别称为“G的叶结点”和“G的内部结点”。
1 算法详述
易知,存在一种切割方法,使一个偶面上的边都是满足条件的边。而无论何种切割方法,都不能使任何奇面上的边都是满足条件的边,至少有一条不满足条件的边。本章将把最大切割问题转化为求解最大奇面对问题,根据第一章提出的“可扩性”定义,对每一层Halin图的扇进行“可扩性”分析、标记并将其收缩为伪点,得到新的Halin图,重复标记和收缩直至得到带有层层标记的轮。从轮开始逐步展开每一层收缩扇,使用优先匹配“向下可扩”的策略,对每一层扇中的奇面进行两两匹配,得到基于初始Halin图的奇面对。
之后将奇面对的公共边标记为“转化边”,基于按层切割原则,将“转化边”的两个端点划入同一集合。对比初步切割的结果,可以看到奇面对的公共边转化为不满足条件的边,却增加了两个面的外部边作为满足条件的边。
1.1 初步切割
扫描Halin图,将每个内部面使用数字(1、2、……)进行编号并做好奇、偶面的标记,两个面的公共边则采用它分隔的两个面的号码对进行标记,例如:奇面1和偶面2的公共边被标记为E=(1,2)。
存在一种尽可能简单的切割办法,将G初步划分成V1和V2。该方法如下:
(i) 任取特征树T的内部结点u,标记为第0层;
(ii) 使用BFS遍历T中的所有结点,将与结点u距离为n的结点标记为第n层;
(iii) 将偶数层(包括第0层)的所有结点划分到V1中,将奇数层的所有结点划分到V2中。
这种办法可以取到G的特征树T的所有边,以及伴随圈C上的一部分边作为切割边。易证这种分层切割办法可以使得每个偶面上的所有边都满足条件,但是每个奇面上恰有一条边不满足条件(即该面包含的外部边)。如果可以找到两个奇面的内部公共边,则在不影响其他面结点划分的情况下,把这两个奇面不满足条件的边都转化到公共边上,就可以减少一条在当前切割集合中的公共边,而增加两条切割边(即这两个面包含的外部边)。
接下来我们采用收缩扇的办法来找出Halin图中最多可能出现的奇面对数,每个奇面对中的两个奇面具有公共边,且一个奇面至多只能出现在一个奇面对中。
1.2 收缩扇
在Halin图中,第一层(最外层)扇中只存在奇面,将第一层的每一个扇进行收缩,如图5:
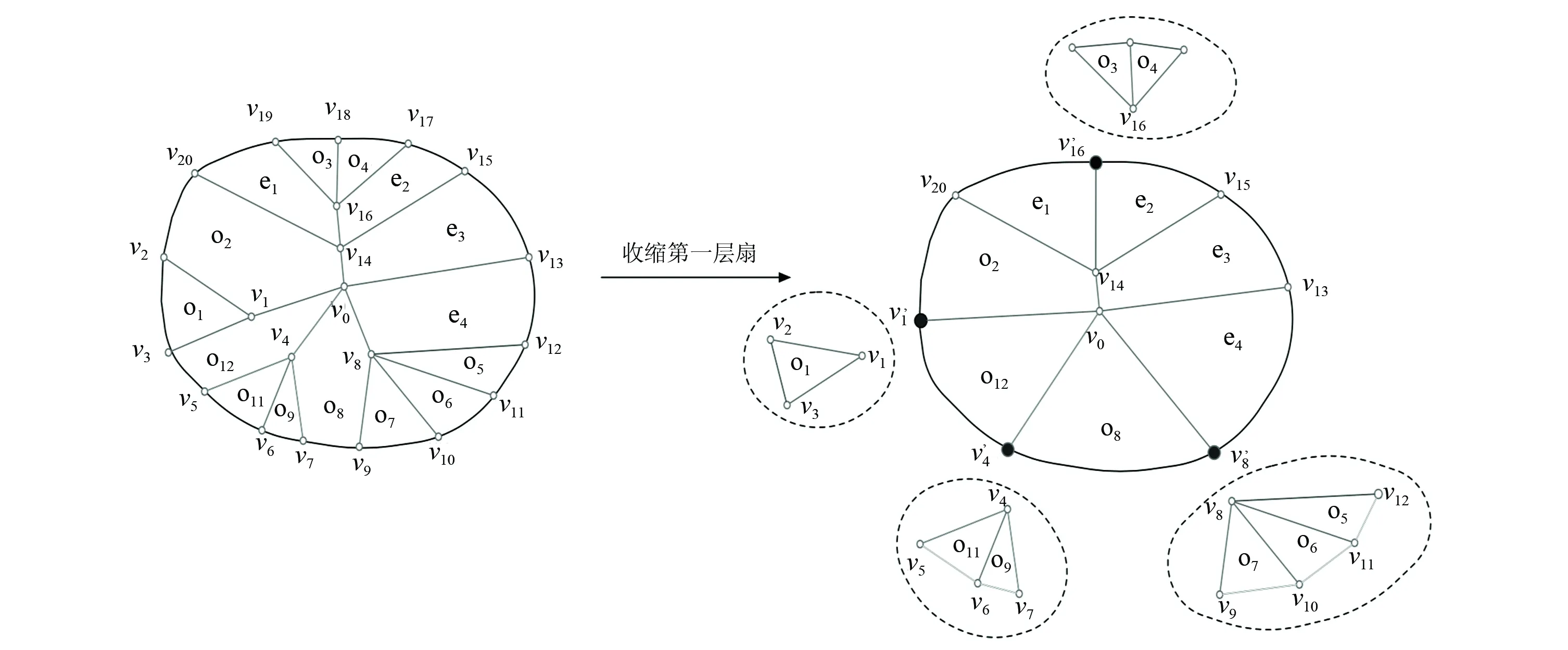
图5 对第一层扇进行收缩Fig.5 Shrink the first layer of fans
(I)若扇中有偶数个奇面,则该组奇面已形成两两配对,扇内取得最大数目的奇面对,该扇标记为“不可扩”;
(II) 若扇中有奇数个奇面,则将该扇标记为“左可扩或右可扩”。
对于第n(n≥2)层扇的收缩情况如下(如图6左图扇中一段连续奇面,包含的叶结点可能是收缩扇的伪点):
(Ⅰ) 标记收缩扇(伪点)的相邻奇面,如图6所示:
(i)如果收缩扇为“左可扩或右可扩”,则相当于在两个相邻面中间插入一个奇面,该奇面可以与左侧或右侧奇面形成配对,若该奇面与右侧奇面进行配对,则在收缩扇内部从左向右两两配对即可,若该奇面与左侧奇面进行配对,则在收缩扇内部从左侧第一个未配对奇面开始,进行两两配对;
(ii)如果收缩扇只能向右扩,或者只能向左扩,则将其可扩方向的相邻奇面标记为“向下可扩”;
(iii)如果收缩扇既可以向左扩又可以向右扩,则将其相邻两个奇面都标记为“向下可扩”;
(iv)如果收缩扇不具有可扩属性,则不对其相邻的奇面做任何处理。

图6 标记收缩扇(伪点)的相邻奇面Fig.6 Mark the adjacent odd faces of a shrunk-fan (pseudo-vertex)
(Ⅱ) 在带有标记的连续奇面上,进行奇面两两匹配,使其成为对集,使用带有“向下可扩”属性的奇面可以对该段奇面进行分割,如图7所示:
(i)对于无属性奇面与“向下可扩”奇面之间片段,“向下可扩”奇面与收缩扇中未配对奇面进行配对,然后向左遍历该段中所有奇面,并进行两两配对;
(ii)对于“向下可扩”奇面与无属性奇面之间的片段,“向下可扩”奇面与收缩扇中未配对奇面进行配对,然后向右遍历该段中所有奇面并进行配对;
(iii)对于两个“向下可扩”奇面中间片段,“向下可扩”奇面与收缩扇中未配对奇面进行配对,并从左侧对一个非“向下可扩”奇面开始,进行两两配对;
(iv)对于两个无属性奇面中间片段,则从第一奇面开始,进行两两配对,如果奇面个数为偶数,则可以进行完全匹配,如果奇面个数为奇数,则需要讨论该片段在扇中位置:
a) 如果该段奇面位于扇中最左端,则从右往左进行匹配;
b) 如果该段奇面位于扇中间或最右端,则从左往右进行匹配。
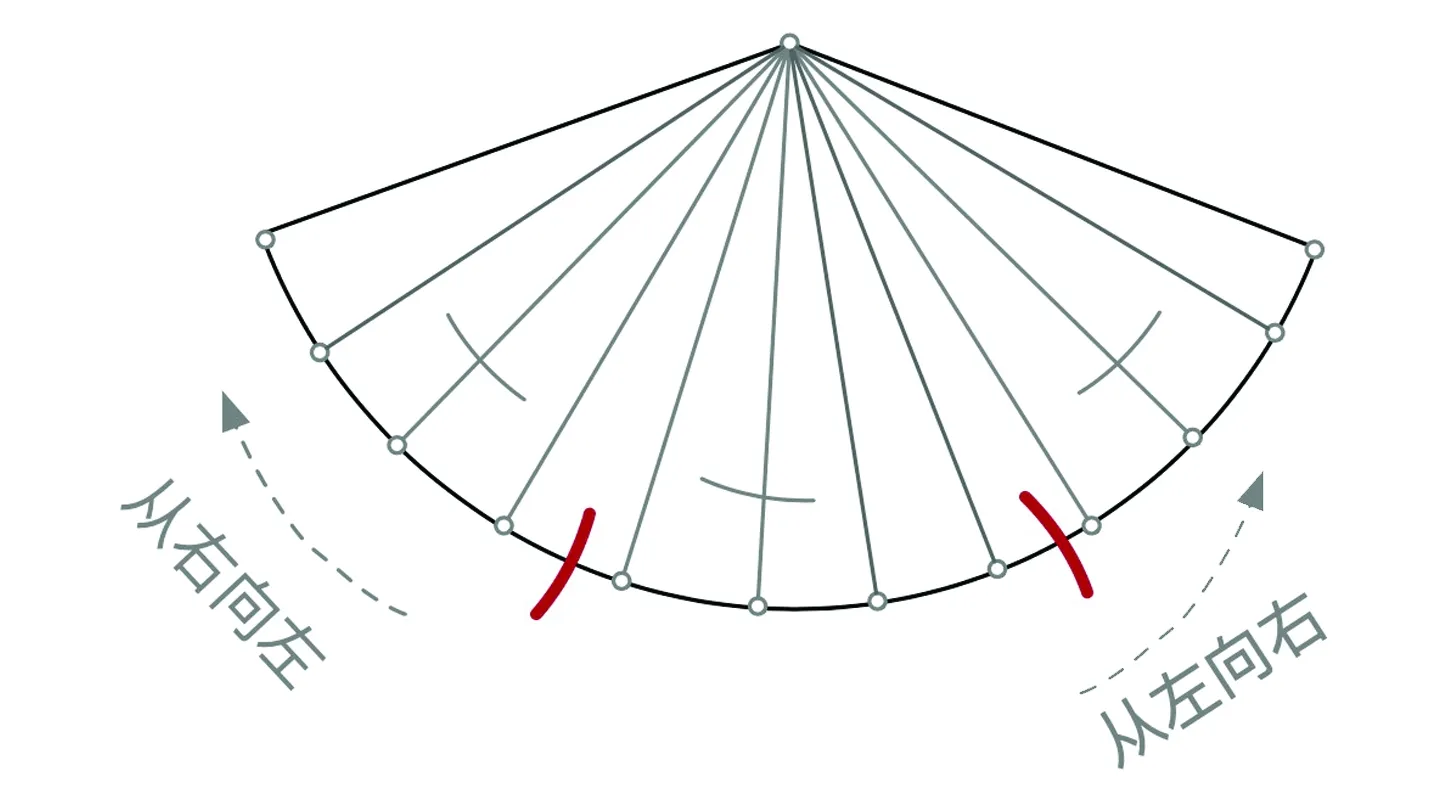
图7 对包含”向下可扩”属性奇面的奇面串进行奇面配对Fig.7 Pairing odd faces in a “down-extendible” segment
(Ⅲ) 对第n层扇进行收缩:
(i)如果该扇左右两端都为偶面,则标记为“不可扩”;
(ii)如果该扇一端为奇面,另外一端为偶面,则对奇面那一侧的最外端奇面进行讨论:如果该奇面处于最左端且未配对,则将该扇收缩且标记为“左可扩”;如果该奇面处于最右端且未配对,则该扇收缩并标记为“右可扩”;如果该奇面已配对,则将该扇收缩并标记为“不可扩”;
(iii)该扇两端都为奇面,如果该扇两端奇面都未配对,则将该扇收缩并标记为“左可扩且右可扩”;如果左端奇面未配对而右端奇面已配对,则将该扇标记为“左可扩”并收缩扇,反之标记为“右可扩”并收缩扇;如果两端奇面都已配对,则标记为“不可扩”并收缩扇;
(iv)注意,如果该扇中不存在偶面和“向下可扩”属性奇面,即该扇为一段连续奇面,如果奇面个数为奇数,则将该扇标记为“左可扩或右可扩”,否则为“不可扩”,并收缩该扇。
对Halin图中的每一层的扇执行以上步骤(Ⅰ)~(Ⅲ)后,当Halin图中不存在可收缩扇时,我们得到一个轮(wheel),轮是一种特殊的Halin图,其特征树的内部结点只有一个。这时,按照步骤(Ⅳ)进行处理。
(Ⅳ) 轮的处理
(i)如果轮上不存在可扩的收缩扇(伪点)且不包含偶面,则从某一奇面开始,进行两两配对,如图8:①;
(ii)若轮上不存在可扩的收缩扇,但包含偶面,则偶面将轮分隔为若干段连续的奇面,则每一段连续奇面从左向右两两配对,如图8:②;
(iii)如果轮上存在收缩扇,则根据步骤(Ⅰ)对收缩扇的相邻奇面进行标记。对于每个“向下可扩”奇面,将该奇面与收缩扇中奇面进行配对。这时,轮中所有偶面和“向下可扩”的奇面将轮中的奇面分隔成若干段连续的奇面,每一段连续奇面从左到右依次进行两两配对,直至不存在相邻的未配对奇面,如图8:③。
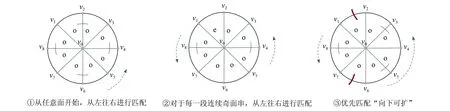
图8 对轮的处理Fig.8 Wheel handling
(V) 展开收缩扇求最大数目的奇面对
当轮中求出最大数目的奇面对后,我们将收缩后的扇逐个恢复。
(i)首先将轮中配对的奇面公共边标记为“转化边”;
(ii)之后将外圈上表示收缩扇的叶结点(伪点)逐个展开成原来的扇,将其中配对的奇面的号码对应的边标记为“转化边”,展开收缩扇进行“转化边”标记,直至不存在表示收缩扇的伪点。配对的算法见步骤(Ⅱ),其中需要指出的是:
a) 若某个奇面是“向下可扩”的,它左边的叶结点是向右可扩的伪点,它右边的叶结点是向左可扩的伪点,则将该面与左边伪点对应的扇的右端未配对的奇面配对,如图9所示。面O1的左右两个叶结点x1及x2均为可扩伪点,其中x1′为“右可扩”,x2′为左可扩,此时,将奇面O1与左边伪点x1′对应扇中的O2进行配对。
b) 若本层扇F中某个奇面对应一个标记“左可扩或右可扩”的具有2k+1个奇面的扇F1:如果在本层扇F中,该奇面与左边的奇面配对,则F1中最左端的奇面与左侧的奇面配对,其余2k个奇面从左到右两两配对;如果在本层扇F中,该奇面与右边的奇面配对,则F1中最右端的奇面与右侧的奇面配对,其余2k个奇面从左到右两两配对;如果在本层扇F中,该奇面不能与左边和右边的奇面配对,则在F1中从左到右2k个奇面两两配对,剩下一个奇面不配对。
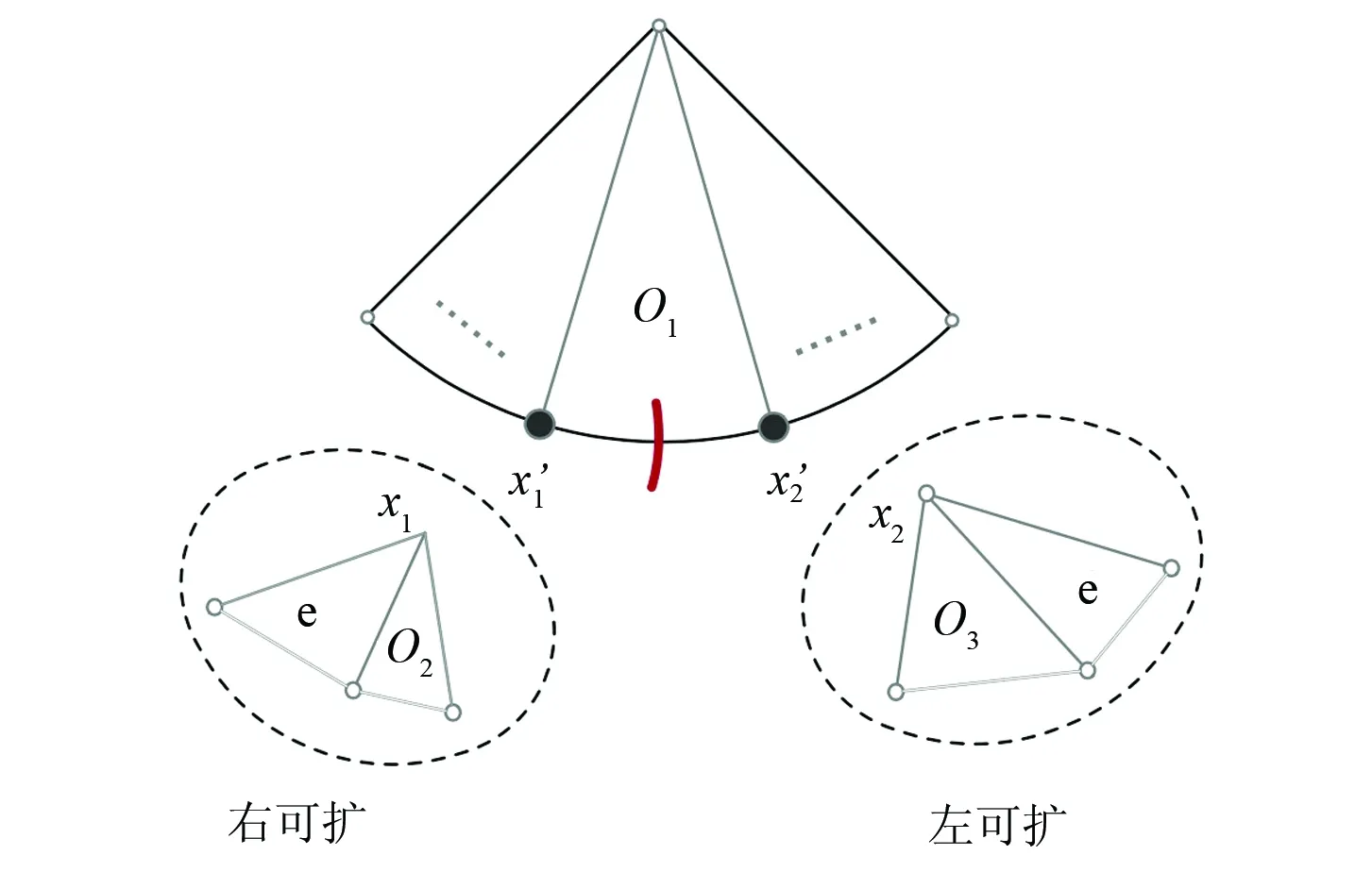
图9 特殊的情况Fig.9 A special case
1.3 最大切割
从某个内部结点u出发(以u为根)进行宽度优先遍历特征树T,首先将u划入集合V1中,若某结点x的父结点y已划入V1(或V2),且xy边不是“转化边”,则x划入V2(或V1);若xy是“转化边”,则x划入V1(或V2)。宽度优先遍历完T,则所有结点都已划入集合V1或V2,这时得到Halin图G的最大切割(V1,V2)。
2 算法分析
2.1 算法正确性证明
定理1按1.2节的算法求出的奇面对是最大数目的奇面对。
证明
(I) 对轮分情况讨论如下:
(i)轮中所有面为奇面,且不存在对应可扩的收缩扇的伪点:则从任意一个奇面开始,从左向右进行两两配对,此时轮中取得最大数目的奇面对;
(ii)轮中所有面为奇面,且存在k个具有“向下可扩”属性的奇面。由于任意两个“向下可扩”奇面之间最多产生1个未匹配奇面,所以轮中最多有k个奇面未匹配。若这k个奇面分别与“向下可扩”奇面进行配对,这样至多增加了k个奇面对,而使原来与“向下可扩”奇面配对的收缩扇中的奇面不再与那些“向下可扩”奇面配对,这样就减少了k个奇面对。其结果小于等于优先选择“向下可扩”的奇面对数目。此时奇面对数目不会大于优先进行“向下可扩”的奇面对数目;
(iii)若轮中存在偶面使得奇面串不构成环,则等同于在扇中讨论该算法的正确性。
(II) 对扇的情形讨论如下:
在扇中,两个偶面之间分隔出一段连续的奇面,或扇的一端和偶面之间分隔出一段连续的奇面,或扇的两端之间是一段连续的奇面(这时扇中全是奇面)。
假设扇的一段连续奇面串中有k个具有“向下可扩”属性的奇面,则最多可将该奇面串划分成k+1段,在第1至第k段中,至多产生k个未匹配奇面。如果不考虑“向下可扩”,则与上面轮的讨论结果相同,奇面对数不会大于优先选择“向下可扩”的奇面对数,对于第k+1段的奇面个数,可以分情况讨论如下:
(i)若第k+1段中奇面个数为偶数,则可以进行完全匹配,在前k段都是奇数个奇面(即至多产生k个未匹配的奇面)的情况下,原奇面串中奇面个数为偶数,若不考虑“向下可扩”,则该k+1段奇面不可扩。若它们就是整个扇,则可以收缩为“不可扩”的收缩扇;若优先将“向下可扩”奇面与收缩扇中奇面进行配对,则会在第1段中产生位于最左端的未匹配奇面。若第一段出现在扇的最左端,在不减少奇面对的情况下,使得该扇收缩后具有“向左可扩”属性,若该扇左侧为奇面,可以在下一轮奇面匹配过程中,可能增加一个奇面对,使得奇面对数可能大于不考虑“向下可扩”的情况。
(ii)若第k+1段奇面个数为奇数,则最后端奇面未被匹配,在前k段都是奇数个奇面(即至多产生k个未匹配的奇面)的情形下,奇面串中奇面个数为奇数,不考虑“向下可扩”时,该k+1段奇面“左可扩或右可扩”。若它们就是整个扇,则该扇收缩后具有“左可扩或右可扩”属性;若优先将“向下可扩”奇面与收缩扇中奇面进行配对,则会在第1段和第k+1段中产生未配对奇面,这两个未配对奇面位于原奇面串的两端,如果它们就是扇的两端,可使得该扇收缩后具有“左可扩且右可扩”属性。如果该扇左右两侧均存在奇面,则有可能增加2个奇面对,所以优先考虑“向下可扩”可能取得更大的奇面对个数。
(iii)假设在一段连续的奇面F中有k个“向下可扩”的奇面,而最大数目奇面对选了其中r个(r 综上,在奇面串进行配对时,优先考虑“向下可扩”的奇面配对,可以取得最大的奇面对数。 定理2按第1节的方法可求出Halin图G=T∪C的最大切割。 证明 G中切割边最多的情况下,每一偶面所有边都是切割边,而每一个奇面至少有一条非切割边(因为它的边界圈的长度为奇数)。首先按1.1节的方法可求出Halin图G的一个初始划分(V1,V2),这时树T中的边都是切割边,偶面上的外部边都是切割边,奇面上的外部边都是非切割边,已达到切割边最多的要求,我们将该切割方法称为初始切割。 要进一步增加切割边数,只能将两个相邻奇面的公共边(只有一条)变为非切割边,而这两个奇面的外部边(有2条)变为切割边。 任取两个奇面f1和f2的公共内部边e1=(t1,t2),和这两个奇面的外部边e2=(u1,u2),e3=(v1,v2),则G-{e1,e2,e3}得到两个分支G1和G2,不妨设t1,u1,v1∈(G1),t2,u2,v2∈(G2)。由1.1节的划分(V1,V2)知,t1和t2分别属于不同的Vi和Vj(1≤i≠j≤2)。而u1和u2(V1和V2)属于同一个Vi(1≤i≤2)(同一个Vj(1≤j≤2))。我们只需将V(G1)中的V1中的顶点与V2中的顶点互换一下,则在不改变其它面的切割边的情况下,t1和t2现在属于同一个Vi(1≤i≤2),而u1和u2(同理v1和v2)现在属于不同的Vi和Vj(1≤i≠j≤2),外部边e2和e3成了切割边,e1变成非切割边,从而G1增加了一条的切割边。 下面我们作一个辅助图A,以证明在G中求最大数目的奇面对后,将每个奇面对的公共边变为非切割边,而它们的外部边变为切割边,可得到最大切割。 设f1,f2,…,fr是G的所有内部面,以f1,f2,…,fr作为辅助图A的结点。设给定G的某个最大切割,A中结点fi和fj之间连一条线,当且仅当G中的fi和fj的公共边为非切割边,最终得到辅助图A。 对于图A中的每一个孤立点fi,若fi对应G中奇面,则fi包含一条非切割边(即外部边);若fi对应G中一个偶面,则fi不含非切割边,即它周界的所有边都为切割边。 若图A中连通分支C的结点数大于等于2,则C中至少有|V(C)-1|条边,这些边都对应G中的非切割边,而C的结点所对应的G中的那些面所包含的非切割边数会大于等于C的边数,因为G中的面可能还包含作为非切割边的外部边。 若C中不存在两个相邻结点fi和fj,且fi和fj都对应G中的奇面,也就是说,C中每个对应奇面的结点fi只与对应偶面的结点fj相邻,即C中至少有一个对应偶面的结点,且C中对应奇面的结点数小于等于|V(C)-1|。而在初始切割中,所有偶面不含非切割边,每个奇面只有1条外部边作为非切割边,故将C中的结点对应的面恢复成初始切割,其中的非切割边数为奇面数,小于等于|V(C)-1|,小于等于在G的假定最大切割中C的结点对应G中的面所包含的非切割边数,因此,该假定最大切割中的切割边数小于等于初始切割。 若C中存在两个相邻结点fi和fj,且fi和fj都对应G中的奇面。取fi和fj的公共边为非切割边,其余边是切割边;C中其它结点所对应的G中的面fk,若fk是偶面,则该偶面不含非切割边;若fk是奇面,则fk恰有一个外部边是非切割边。因此,我们在C的结点对应的面中找一个奇面对,将它们的公共边转化为非切割边,可以使得这两个奇面的外部边都变成切割边,而不对其它面产生影响,将其它面恢复成初始切割后,C的结点对应的G的面的非切割边数小于等于|V(C)-1|,小于等于G的假定最大切割中C的结点对应的G中的面所包含的非切割边数,即其切割边数大于等于当前C对应的面中的切割边数。 通过辅助图A,我们可以证明,在给定的最大切割中,G中的非切割边数大于等于G中取s个奇面对的公共边作为非切割边,其余奇面取它们包含的外部边作为非切割边的非切割边数,其中s为A中满足以下条件的连通分支数,每个连通分支含两个相邻的结点fi和fj,且fi和fj都对应G中的奇面。 由前面的证明可知,在G中找到的奇面对越多,将其公共边转化为非切割边后(其外部边转化为切割边),则G中的切割边就越多。因此,只要在G中找出最大数目的相邻奇面对,将每一对奇面的公共内部边(比如e1)变成非切割边,而将它们的外部边(如e2和e3)变成切割边,即可得到最大数目的切割边。这也就是在1.3节中将“转化边”(对应上述的e1)两端点划入同一分类Vi(1≤i≤2),对T中非“转化边”,将T中相邻的两点划分入不同的分类Vi和Vj(i≠j)。因此,1.3节所得到的分类(V1,V2)是最大切割。 第一步,扫描Halin图,对每个内部面使用数字(1、2、……)进行编号并做好奇偶面的标记,两个面的公共边则采用它分隔的两个面的号码对进行标记,例如:奇面1和偶面2的公共边被标记为E(1,2)。其中每条内部边被扫描次数为2,此时,时间复杂度为2n-1(n为顶点数);每条外部边扫描次数为1,时间复杂度小于顶点数n。所以第一步时间复杂度小于3n。 第二步,收缩扇和扩展扇,将奇面对公共边标记为“转化边”,该过程遍历了两次G中所有的面,由于面数小于顶点数,所以该步骤中,时间复杂度小于2n。 第三步,宽度优先遍历T中所有顶点,并划分到割集的两个集合中,该步骤时间复杂度为n。 综上,该算法的实际运行时间为6n,时间复杂度为O(n)。2.2 时间复杂度分析

