基于数据挖掘的快消行业销售预测

叶剑锋， 郑国英

(上海交通大学 软件学院, 上海 200240)

0 引言

随着第三次工业革命以来信息科技的迅速发展，各行各业都积累了海量异构的数据资料。这些数据往往都具有丰富的数据价值，急需从这些信息里抽取出商业价值、业务知识，从而辅助支持于决策[1]。通过数据挖掘技术[2-3]来进行预测性分析，可以挖掘企业有效数据，提取价值信息，帮助企业做出战略性决策。

销售预测通常是根据商品过往数据和目前经济形势环境等情况来预测短期或者长期商品销量，评估市场情况。销售预测是企业供应链管理的关键环节，精准的销售预测，对商业公司生产管理，商业决策具有深远影响。

快速消费品(快消)[4]为高频次采购的商品，它具有低成本、低价格、多非理性、购买次数多等特点。快速消费品的促销活动一般来说都能带来很大幅度的销量提升，带来商品的大卖。在瞬息万变的商业环境中，能否比竞争者提供更低的成本至关重要，这就需要进行正确及时的产品销售预测。

本文为快消企业提出一个综合考量内外部变量的精准销售预测解决方案，能够根据企业历史销量以及未来促销计划对未来销量进行预测，并且设计与实现了一个预测工具。

1 需求分析

本文为某一快消巨头Z公司研发销售预测工具。Z公司在零食、饮料、饼干等零售上全球领先，旗下拥有多个著名品牌。Z公司经常会在不同时期利用不同主题进行促销，如“儿童节满119减30”和“母亲节买二送一”等不同促销活动，除商家自身举办的促销活动外，电商平台本身也会有各种促销活动，例如双十一大规模促销活动。

在数字化时代，Z公司需要一个预测工具来完成精准的销量自动预测，具体地，销售预测工具应实现以下需求：

1) 对不同SKU(Stock Keeping Unit，库存量单位)商品进行预测，并实现商品数据的交互输入。

2) 对商品进行不同时期长度的预测，根据业务需求，快消行业特点进行预测时间长度的调控。

3) 对不同商品进行不同季节周期的预测。基于不同业务背景，商品销售的季节性周期可能会有所不同，需要满足即使调控。

2 基于改进时间序列模型的销售预测

2.1 改进的季节性ARIMA模型

Z公司的主打商品，作为快速消费品的典型商品，其商品在春节、节假日等时期具有明显周期性峰值，也就是其销量序列具有明显周期性。在一个时间段中，序列观测值yt和yt-s呈现出相似情况，比如同处于波峰同处于陡然上升，那么S就是该序列的周期。

建立季节性ARIMA(P,D,Q;p,d,q)模型，需要确定P,D,Q,p,d,q等参数。差分阶数的确定通过判断几阶差分后是否平稳即可，而自相关，偏自相关系数的确定则需要确定对应函数及画自相关图，偏自相关图来分析，这一步骤通常比较繁琐。

模型选择关注模型的潜在变量和模型的可能形式[5]，模型应当追求负责精度与复杂度，但提高模型复杂度会带来一个机器学习中非常普遍的问题——过拟合。模型选择没有绝对标准，因为标准是根据数据分布的，并且要能融入到统计推理的框架中去。通常用AIC(Akaike Information Criterion，赤池信息准则)和BIC(Bayesian Information Criterion,贝叶斯信息准则)来进行模型选择。BIC和AIC都试图通过引入模型中参数个数的惩罚项来解决这个问题；在BIC中惩罚项比AIC中的惩罚项大。AIC定义为：AIC=2k-2ln(L)

通常，当模型复杂度提高(k增大)时，似然函数L就会增大，AIC就会变小，但是k过大时，似然函数开始缓慢增加，导致AIC增大，模型过于复杂，容易造成过拟合现象。目标是最小化一个好的模型的AIC或BIC值。对于被调查的模型的范围，这些准则中的一个值越低，模型就越适合数据。

通过上述分析，可以发现,对于ARIMA模型参数选择问题，可考虑用ARIMA模型的AIC法则进行定阶[6]，求出最小AIC值得p，q，进而采用ARIMA(p,q)。同样对于季节性ARIMA模型，可以通过AIC来对[P,D,Q,p,d,q]进行定阶，求出最小AIC值，求得参数。

本文在R里，通过循环语句遍历参数取值范围来找出最小AIC参数组合。即对参数P,D,Q,p,d,q在其取值范围内进行遍历，对于每个组合，求得模型的AIC值，找出最小AIC的模型，找到对应P,D,Q,p,d,q,得到最佳模型参数。

2.2 销售预测方法

本文预测所需数据来自Z公司的数据仓库中的电商平台销售报表，如表1所示。

表1 Z公司销量报表

其中，统计日期颗粒度是到日，截至项目期商品销售日期是从2015-2017，为短时期序列，商品ID，商品标题，SKU编码，条形码为商品标签，确定每一个不同商品，销量即为本文挖掘分析的变量。

本文针对Z公司的真实业务需求，其快消品需要进行多商品的考虑季节性影响因素的精准预测，基于季节性ARIMA时间序列模型，提出了一种销售预测方法，如图1所示。

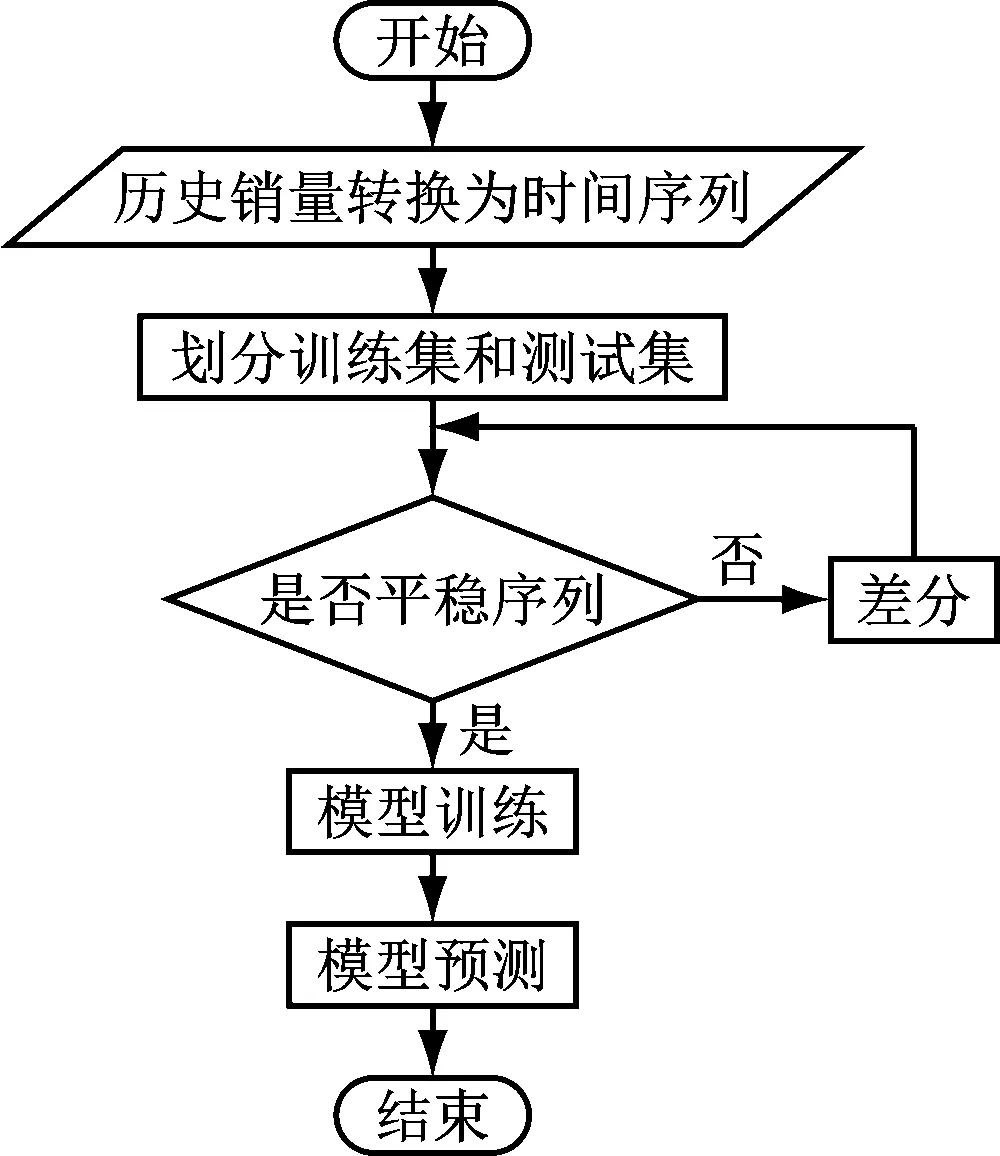
图1 销售预测方法

该方法由五个步骤组成。

1) 历史销量数据转换为时间序列。将销量数据转换为时间序列数据。

2) 划分测试集和训练集。对序列进行划分，确定训练集测试集。

3) 平稳性检验。对序列平稳性进行判断，不平稳，则需要进行差分转换为平稳序列。

4) 模型训练。使用训练数据训练出改进的季节性ARIMA模型。

5) 模型预测。使用训练得到的ARIMA模型来预测。

Top1商品的销量序列图由图2所示。

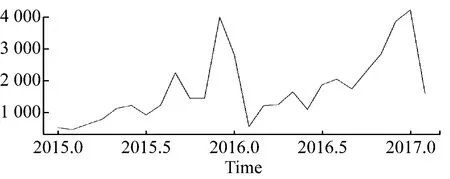
图2 Z公司销量Top1 SKU时序图

可以看到销量走势大致为上升趋势，不同年份之间月度销量走势相似，即具有一定的季节性。

针对此26个月长度范围商品序列，将最后两个月作为测试集，将前两年数据来进行训练。使用ARIMA模型来建模，首先需要对该序列作平稳性检验分析。经过一阶差分后，可以看到 p-value<0.01, 序列平稳，那么可以对平稳序列进行ARIMA建模。

本文采用ARMA模型的AIC法则进行定阶，求出最小AIC值得p，q，进而采用ARMA(p,q)。同样对于季节性ARIMA模型，也能够使用AIC来确定[P,D,Q,p,d,q]值，求出最小AIC值，得到模型参数。

2.3 评估与测试

本次建模，按照Z公司常用衡量指标，同时由于是时间序列，需要看到每月预测精确度，对单个Sku商品逐月预测，本文采用绝对误差。

Accuracy=1-error

按照Z公司要求，对Z公司要求的销量Top20商品进行了最新未来一个月的预测，预测结果如表2所示。

3 基于改进时间序列多元回归组合模型的销售预测

3.1 组合模型

快消业的促销很大程度地决定销量，其他因子影响微乎甚微，那么这时用多元回归来预测就会出现预测不准确。因而既需要将强影响因子纳入模型，考虑它的影响系数，在没有其他因子的情形下，自然只有因变量自身的影响，即对应于销量预测，考虑它的历史销量以及促销因素，需要将自身因素与外部唯一强影响因子同时进行建模，如果能将两个模型进行结合，发挥各自功能，自然就能做到这点。基于此，本文研发出基于改进时间序列与多元回归的组合模型。

表2 预测结果准确率

基于改进时间序列与多元回归组合模型流程如图3所示。

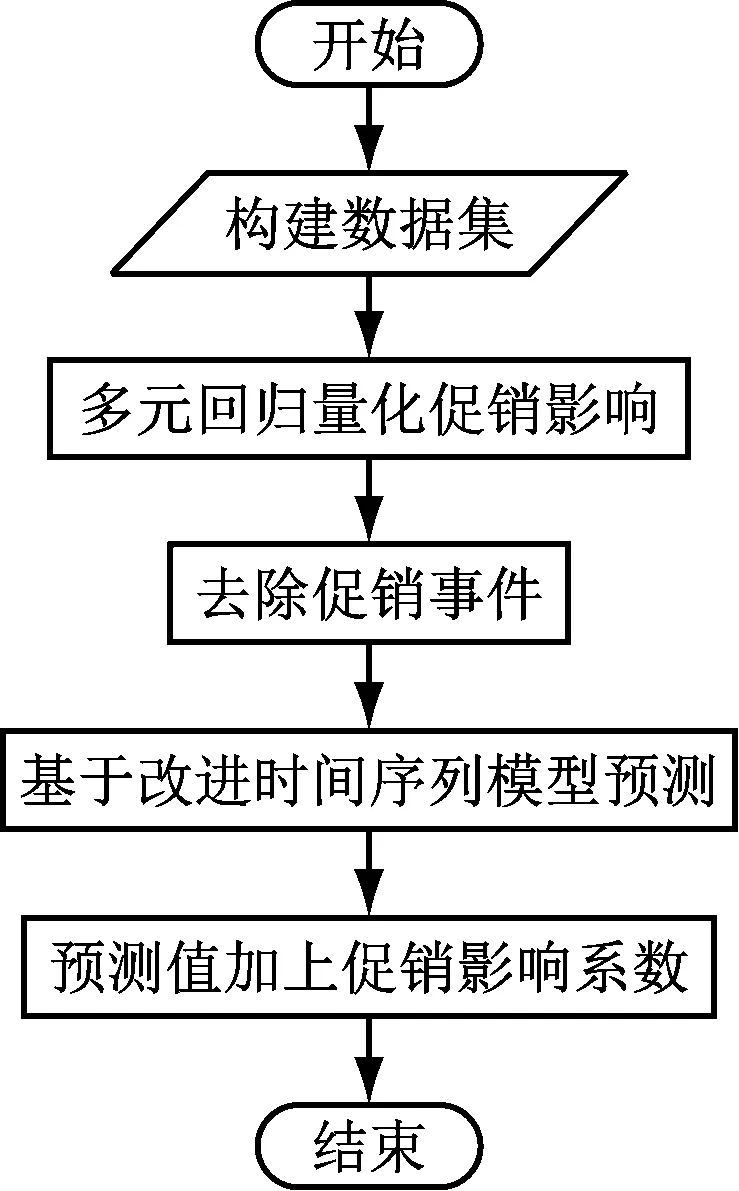
图3 基于组合模型的销售预测

即首先需要构建模型所需数据集，进行建模之后，使用多元回归模型对数据集进行训练，得到促销事件对销量的影响系数，假设历史中没有促销事件，模型将历史数据集里促销因子Remove，基于此数据使用多元回归predict, 使用改进季节性ARIMA模型在此数据集上进行预测，最后加上促销因子影响系数，即得到最终预测值。

3.2 构建数据集

Z公司在促销上的行为是在某段时期内进行不同主题不同等级促销，本文拿到数据如表3所示。

表3 促销活动日历

其粒度到天，对于回归建模需要粒度到天的一组映射关系，数据集构建如表4所示。

3.3 多元回归量化促销事件影响

构建促销等级，年，月，日对销量的映射，

>fit<-glm(data=time_data_train,Quantity～factor(Level)+factor(Year)+factor(Month)+factor

(Day_31),family = gaussian)

即多元线性回归建模，完成销量拟合fit。当需要量化出促销对销量影响时，可以使用回归系数。回归系数(regression coefficient)表示了自变量x对y有多大的影响程度。提取出这些因子的回归系数：

>d_coe=data.frame(fitcoefficients)

Coefficients:

Estimate Std. Error t value Pr(>|t|)(Intercept) 41.546 8 10.804 4 3.845 0.000 135***factor(Level)A 23.400 3 11.759 2 1.990 0.047 111*factor(Level)S 23.937 9 6.003 8 3.987 7.63e-05***factor(Level)S+GSKA -4.064 2 7.836 8 -0.519 0.604 254 factor(Level)S+GSKA+SBD 21.566 0 24.304 5 0.887 0.375 308 factor(Level)X1 -67.704 8 24.349 9 -2.780 0.005 622**factor(Level)X2 -20.592 1 16.635 1 -1.238 0.216 317 factor(Level)X3 -14.497 4 21.962 6 -0.660 0.509 482 factor(Level)X4 9.523 7 24.969 4 0.381 0.703 049 -

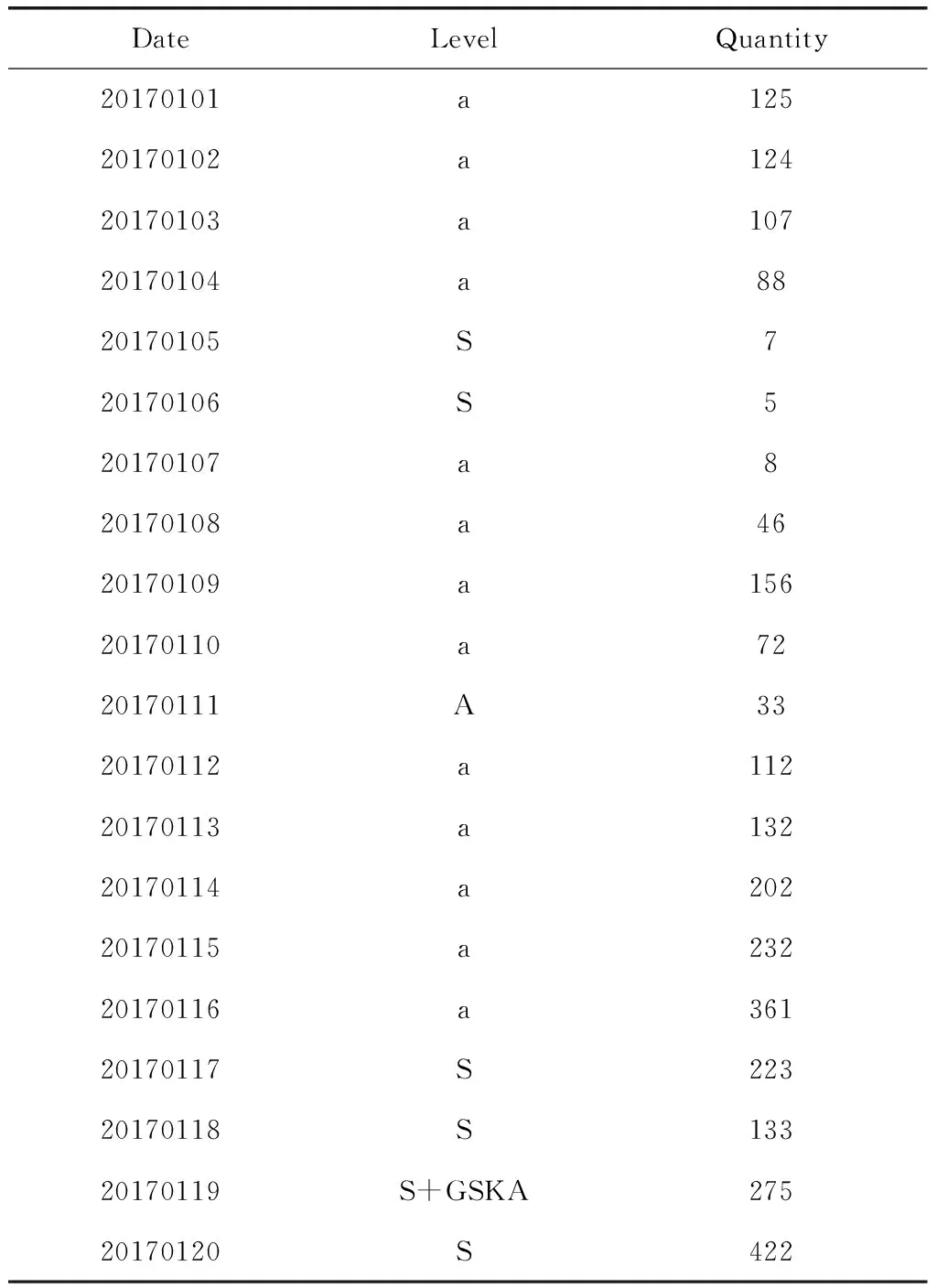
表4 数据集

可以看到，Level A,Level S的促销对于销量具有显著影响，回归系数都约为23，系数越大表明一个因子变化的大小对销量影响越大。这里即举办Level A/S的促销一天，即能带来约23个/袋的销量提升。

3.4 去除促销事件

本文假设原始数据集里没有进行促销事件，我们将原数据标记为无促销：

>df_no_event[["Level"]]="a" #Level a 表示没有促销

用没有促销事件的历史数据集基于有促销事件的真实拟合fit来作回归预测，

>data_no_event_pred=predict(fit, df_no_event)

3.5 基于改进时间序列预测

之后，用此多元回归假设没有促销时间的预测数据来作时间序列建模，算法伪代码如下：这里将日销量累计到月销量，进行月度的季节性ARIMA建模,依然使用之前研究的改进的季节性ARIMA模型。至此，完成了时间序列建模，得到到月的预测值0r。

3.6 加上促销影响系数

本文的模拟机制是假设去除促销，在其他变量不变的情况下，需要将促销因子重新纳入模型来评估促销的影响。可以看到促销数据是到天的，得到了不同等级促销日影响系数，这里的时间序列建模是到月度的预测，因而对未来月份的预测，可以累计月促销天数，将不同等级促销影响加入到模型：

coef=d_coe[d_coe['index']==factor_level,]$fit.coefficients

or[or['month']==temp_month,]$x=or[or['month']==temp_month,]$x+temp_days[j]*coef

即在时间序列预测月份销量上，加上促销天数带来的销量提升。

3.7 工具实现

基于上述研究开发的自动化工具，对于混合模型也提出自动化功能需求。一是历史销售数据的交互式输入，二是未来促销计划的交互式输入，三是预测长度的交互。基于ui.R,设计框架，对于算法模型，使用server.R封装。程序流程图如图4所示。

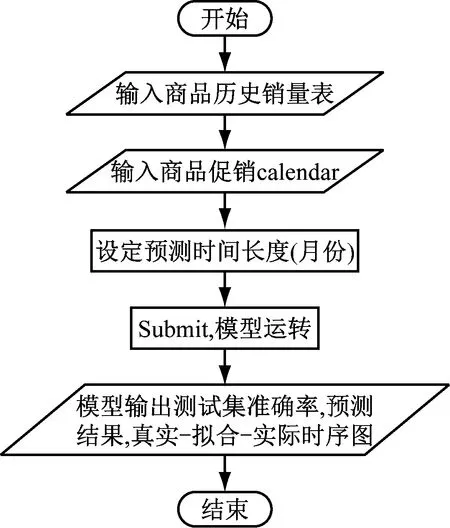
图4 程序流程图

以上内容的开发封装，得到自动化预测界面如图5所示。左栏第一行为输入商品历史数据，第二行为输入促销计划日历，调整预测长度，可得到未来月份的预测值。

图5 组合模型预测工具界面

3.8 评估与测试

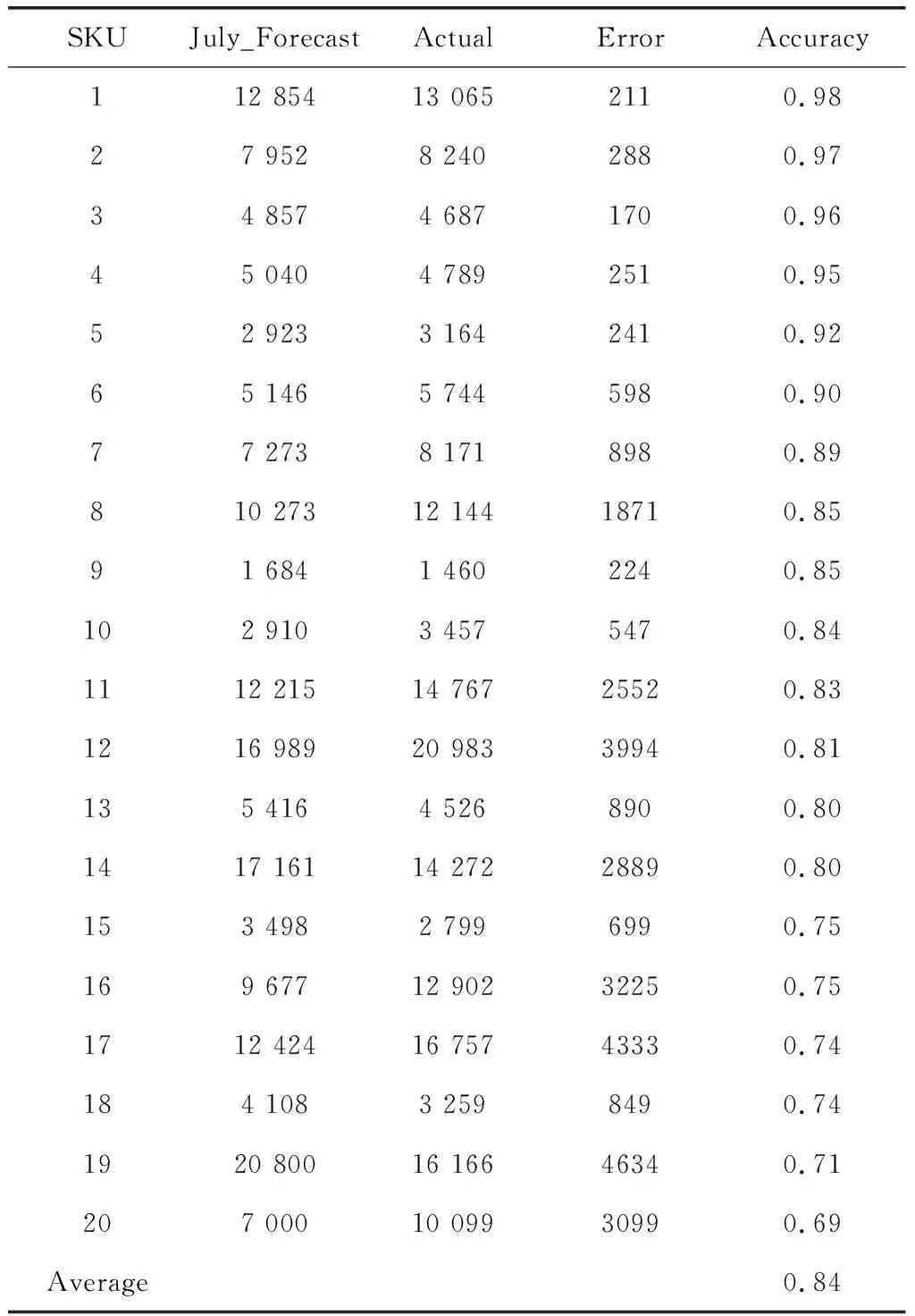
表5 组合模型预测结果

可以看到，相比于单一的季节性ARIMA模型，对于所选择20个商品，预测平均准确率有约5%的提升。另外，预测工具训练时间为35 s,整个工具一键预测运行67.5，达到企业测试要求，工具可以平稳运行。

4 总结

为了帮助快消企业作出准确的采购等商业决策，本文基于企业现有数字化能力和设施，建立一个预测模型来帮助精准预测销售，利用历史销量数据和促销日历数据来进行模型训练，既利用了商品自身数据又利用了外部促销因素，通过预测分析的结果来给企业予决策支持。

本文主要工作如下。

1) 基于改进时间序列模型的销售预测方法研究

对快消企业数据进行挖掘分析，完成从ARIMA到改进季节性ARIMA模型的设计，考虑了快消行业的季节性周期特点、周期长度不同的特点，不同商品历史数据长度不同特点。

2) 基于组合模型的销售预测方法研究

针对快消企业的促销因素，研发基于季节性ARIMA时间序列与多元回归组合的模型。在已有历史数据的基础上，纳入企业促销因子，实现更精准预测，同时量化验证了企业促销的有效性。

3) 自动化预测工具的开发

基于上述研究成果，采用R语言和R-shiny框架等技术完成对算法的封装以及自动化预测功能，实现交互式简易预测，满足企业业务人员使用需求。本文采用企业实际数据进行了实验与测试，结果表明，工具所实现的两种模型分别预测准确率达到79%和84%，预测时间分别为11.5 s和67.5 s，达到预期目标。