基于属性熵的隐私匿名信息保护研究与应用

贾步忠

(陕西财经职业技术学院 会计二系, 咸阳 712000)

0 引言

随着现代化智能技术的高速发展，各类智能系统在给人们的生活带来便利的同时，也给人们隐私信息的安全性造成了极大的威胁。目前，大部分企业为了适应市场需求的变化，纷纷开始对用户数据进行深入挖掘，以此获取对其更加有利的信息。然而，这些被各企业深入挖掘出的信息并不具备安全性，其中大多包含一些人们不愿泄露的隐私及敏感信息。许多不法分子为了谋取利益，试图通过攻击各企业数据库的方式来获取人们身份信息。人们身份信息一旦泄露，将会对人身安全及财产安全造成极大的威胁，严重影响人们的正常生活与工作。

在隐私信息保护研究领域中，已存在许多隐私敏感信息保护方法。如王超(2015)一种轨迹特征及动态邻近性信息保护方法，从而通过最小化邻域扭曲密度的方式来解决信息损失的问题[1]；马飞等[2-7]采用文献综述的方式，对当前匿名信息保护的研究进展进行了综述，分别比较了基于k-匿名、Markov链、聚类、随机化等匿名保护方法的优缺点；这些方法虽然能够对人们隐私信息起到一定的保护作用，但保护的同时，很多方法都会对原数据的完整性造成不同程度的破坏。因此，如何在保护隐私信息不被泄露的同时，又能保障原数据的完整性成为隐私信息保护领域研究的首要难题。当前，大部分隐私匿名法在对隐私信息进行保护时，主要是对准标识符属性与敏感属性进行保护，却并未对不同准标识符属性与敏感属性之间的影响进行考虑，从而使部分攻击者通过链接攻击以及同质攻击就可轻易获得用户隐私信息。基于此，本文提出一种基于权重属性熵的分类匿名法，应并将其应用到隐私信息保护领域中，并对其可行性进行验证。

1 基于权重属性熵分类匿名模型

1.1 模型构建思路

对该模型的构建，首先以信息熵作为参考，对准标识符属性对于敏感属性分类的重要性进行估量；然后，对隐私数据损失度知道属性匿名丢失情况进行构建；最后，以分类匿名保护度的变化为基础，对分类重要性及隐私匿名算是标准的最优平衡进行确定，以此赋予数据分类准确性及隐私性。

1.2 权重属性熵的度量

站在PPCM中匿名分类方法的角度[8-10]，假设属性QI具备的不确定性较小，则代表属性QI具备较高的纯净度，那么属性QI将具备较佳的分类准确性效果。在属性不确定性衡量方面，熵属于一种衡量属性不确定性的分裂方法。通常情况下，熵主要通过Top-down方式对属性进行分裂。

假设E(x)为某一随机变量X的熵，那么E(x)的定义为式(1)。

(1)

假设设定的样本数据表D当中具备类别属性{C1,C2,…,Ck}，其中包含k个类别属性，样本数据表D中具备Si(i=1,2,…,k)个属于类Ci的元组。那么，此时可将给定D中数据分类信息熵E(S)定义为式(2)。

(2)

假设属性Q中具备v个不同的值{q1,q2,…,qv}，数据表D被Q划分成为v个子分区{D1,D2,…,Dv}，其中Dj(j=1,2,…,v)包含D中属于Q属性值为qj的所有元组，属性Q在对D的分类区域进行划分时，正是需要权重全属性这一分类量。由此，权重属性熵E(Q)可表示为[11]式(3)。

(3)

权重属性熵增量ΔE即为E(S)与E(Q)之间产生的增量，因此ΔE可表示为式(4)。

ΔE=E(S)-E(Q)=E(S1,S2,…,Sk)-E(Q)

(4)

根据上式可得出结论：E(Q)值越小则分类效果越优，即权重属性熵增量ΔE影响分类效果的优劣，其值越大则分类效果越优。

权重属性熵增量ΔE适用于数据表D数内Q出现较多的情况。但是，在通过权重属性熵增量ΔE对分类准确性进行分析时，无法避免偏重问题。针对这一问题，可以通过权重属性熵增量比率ΔE′来解决。ΔE′为ΔE与属性Q的信息熵的比值，可表示为式(5)、式(6)。

ΔE′=ΔE/E(Q)′

(5)

其中,E(Q)′即属性Q的信息熵:

(6)

根据式3与式5可以得出结论：权重属性熵增量比率越大，则分类的准确性则越优。

1.3 隐私数据损失的度量

属性QI包含了分类属性与数值属性，在进行隐私保护的过程中会导致属性信息损失。对此，采取加权确定性代价的方式，在获取属性QI隐私属性的过程中进行匿名损失信息度量[12-15]。

(1) 分类型属性匿名损失

对于给定属性QI={QC1,QC2,…,QCm1,QN1,QN2,…,QNm2}，其分类属性为QCj(j=1,2,…,m1)，对应的分类树为Tj(j=1,2,…,m1)。对于任意元组t中的任意某一分类属性，将其值vj匿名泛化后得到先祖节点值pj，由此可将分类属性的匿名损失表示为式(7)。

(7)

其中，k为S值的数量，wj为QCj(j=1,2…,m1)的分类权重，|pj|为pj内的叶节点数量，|Tj|为Tj内的叶子节点数量。

匿名泛化后，分类属性匿名损失为式(8)。

(8)

(2) 数值型属性匿名损失

对于给定属性QI={QC1,QC2,…,QCm1,QN1,QN2,…,QNm2}，其数值属性为QNj(j=1,2,…,m2)，对应的取值域为QDj(j=1,2,…,m2)。对于任意元组t中的任意某一数值型属性，将其值bj泛化后得到对应区间[aj,cj](aj≤bj≤cj)，由此可将数值型属性的匿名损失表示为式(9)。

(9)

其中，k为S值的数量，wj为QNj(j=1,2…,m1)的分类权重，|QDj|=max(QNj)-min(QNj)。

匿名泛化后，数值型属性匿名损失为式(10)。

(10)

(3) 所有元组匿名损失

对于给定属性QI={QC1,QC2,…,QCm1,QN1,QN2,…,QNm2}，其分类属性为QCj(j=1,2,…,m1)，对应的分类树为Tj(j=1,2,…,m1)，其数值属性为QNj(j=1,2,…,m2)，对应的取值域为QDj(j=1,2,…,m2)。元组t匿名泛化后元组匿名损失为式(11)。

PL(t)=PLQCj(t)+PLQNj(t)

(11)

由于D的PL(D)为数据表内各PL(t)的和，因此D的匿名损失为式(12)。

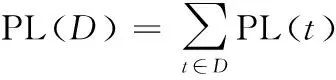
(12)

1.4 分类匿名保护的度量

分类匿名保护度cap为ΔE′与PL(D)的比值，表示为[16]式(13)。

(13)

分类匿名保护度cap越大，则分类效果越优。根据式13可知，ΔE′越大则分类匿名保护度cap越大，PL(D)越大则分类匿名保护度cap越小。

1.5 基于权重属性熵的分类匿名模型构建

针对各种准标识符属性对敏感属性的分类影响问题，为了满足数据分类应用的匿名要求，采用了一种基于权重属性熵的分类匿名算法。该算法基于分类熵概念，通过匿名方式来完成数据集的等价分类，并以分类匿名保护条件来解决分类效果与隐私信息损失之间的问题。具体核心步骤为：

(1) 对于给定的样本数据表D,通过计算敏感属性S的信息熵E(S1,S2,…,Sk)，得到QI对敏感属性S的熵值，以此来直观地展现分类信息；

(2) 计算ΔE与属性Q的信息熵的比值ΔE′，以此判定各属性Q对敏感属性S的分类重要程度，并且通过将分类权重熵增量比ΔE′值进行排序，有效选择分裂结点；

(3) 将max ΔE′的属性QI作为分裂节点，并通过分类匿名保护度cap判定分类效果与隐私信息损失之间的平衡，然后根据分类能力对分裂属性进行等价划分并保存；

(4) 对上述进行递归操作，遍历分类树后对余下叶子结点进行匿名操作，将其等价分类，直至满足匿名要求后，输出匿名后的结果。

2 实验与分析

2.1 数据可用性分析

对于数据可用性，主要采用数据分类准确性进行分析检验，具体方法是通过分类树C4.5分类模型以及贝叶斯分类模型，将本文所提出的基于权重属性熵的分类匿名算法与原始数据集、Top-down算法以及IACK算法进行对比，以此分析验证分类准确性。

将准标识符属性个数设为8，参数值K={2,4,6,8,10}。原始数据oridi-data与各算法在分类树C4.5分类模型上的分类精度情况如图1所示。

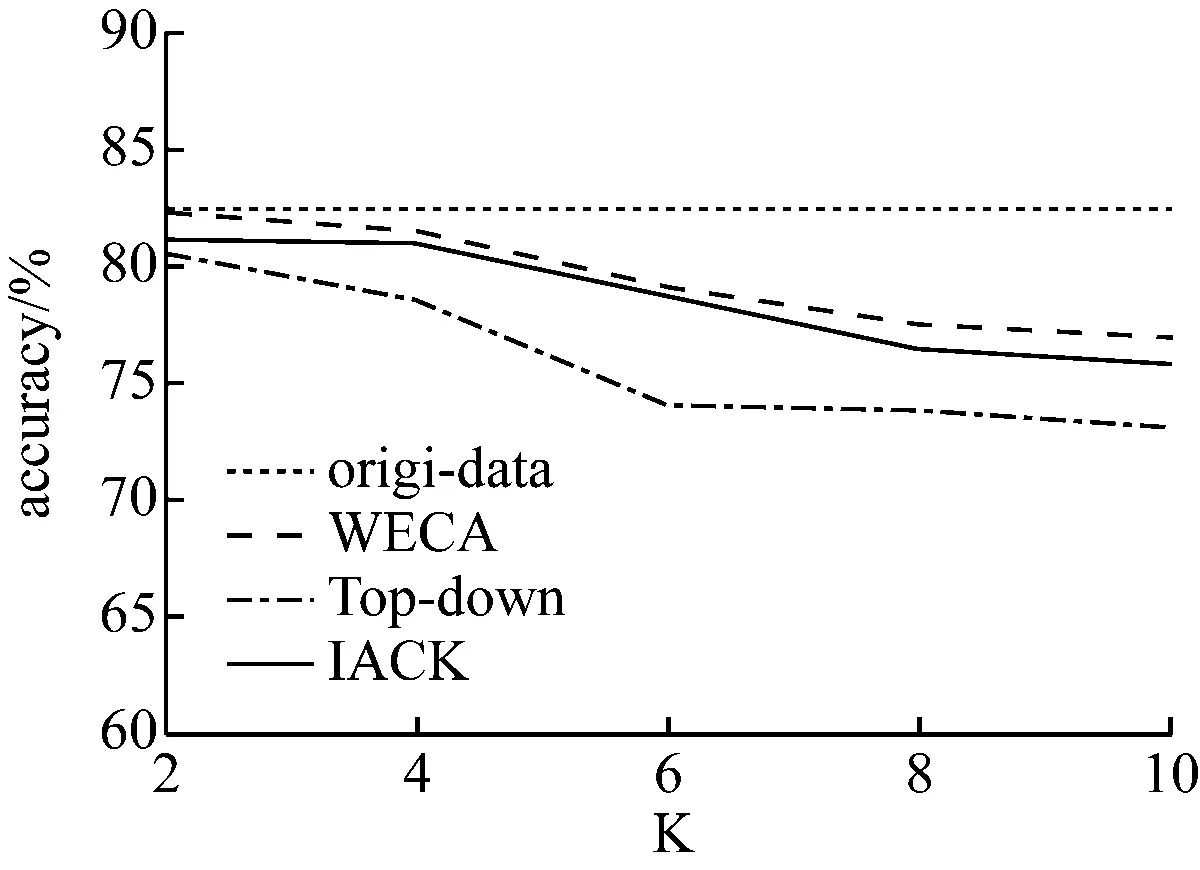
图1 分类树C4.5分类模型上的分类精度

原始数据oridi-data与各算法在贝叶斯分类模型上的分类精度情况如图2所示。

从图1与图2所示的对比情况可以看到：原始数据oridi-data未经过匿名处理，因此其分类准确性并没有随K值的变化而变化；三种算法则由于隐私处理过程中的匿名泛化操作而导致属性信息损失，因此三种算法的分类准确性随着K值的持续增大而不断降低。相较而言，本文所提出的基于权重属性熵的分类匿名算法(WECA)的分类精度，其最低值为77%，在整体上高于其他两种算法的分类精度。由此可知，基于权重属性熵的分类匿名算法(WECA)具有较高的分类可用性。

图2 贝叶斯分类模型上的分类精度

2.2 匿名信息损失分析

对于匿名信息损失，主要采用隐私数据损失衡量进行分析检验，具体方法是将基于权重属性熵的分类匿名算法(WECA)与Top-down算法以及IACK算法在不同K值下的匿名信息损失进行对比，以此进行分析验证。

将准标识符属性个数设为8，参数值K={2,4,6,8,10}，三种算法在不同K值下的匿名信息损失对比情况如图3所示。

图3 不同K值下的匿名信息损失

如图3所示，三种算法的隐私匿名损失随K值增加而相应增加。分析其原因，是因为等价类中元组数量随着K值的增加而增加，导致三种算法的准标识符属性泛化程度提高。相较而言，IACK算法的匿名信息损失最大，而基于权重属性熵的分类匿名算法(WECA)的目标为分类匿名保护度最高，通过分类匿名保护度cap判定分类效果与隐私信息损失之间的平衡，因此其匿名信息损失则相对较小，平均约为18%。

将参数值K设为K=6，准标识符属性QI设为|QI|={2,4,6,8}。三种算法在不同QI值下的匿名信息损失对比情况如图4所示。

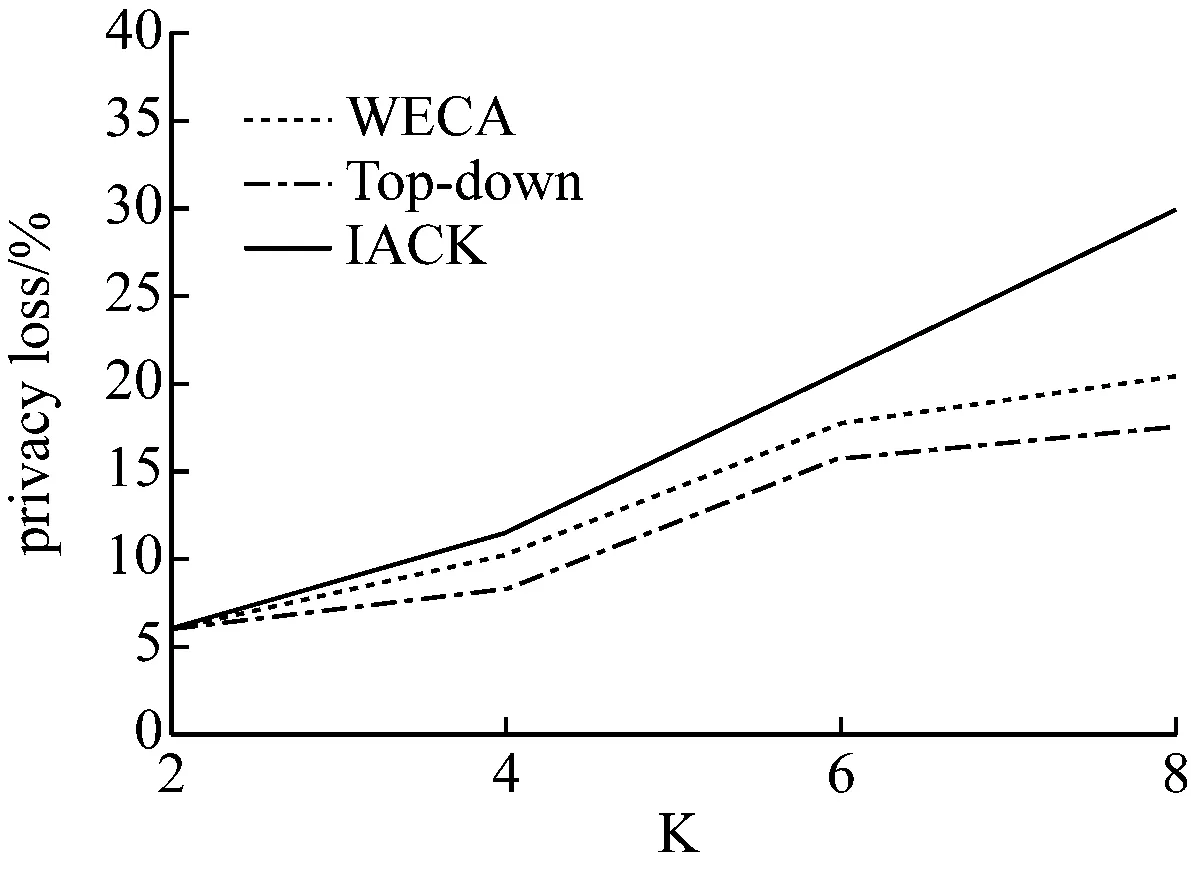
图4 不同QI值下的匿名损失

如图4所示，三种算法的隐私匿名损失随准标识符属性QI增加而相应增加。分析其原因，是因为等价类中需泛化的属性数量随准标识符属性QI的增加而增加，导致三种算法的隐私匿名损失增加。相较而言，IACK算法由于采用互信息熵进行属性泛化，筛除了所有不满足匿名要求的信息，因此其匿名信息损失最大，而基于权重属性熵的分类匿名算法(WECA)的匿名信息损失则相对较小。

2.4 执行时间分析

对于执行时间，本文主要是在准标识符属性恒定而K值不断变化的情况下，对基于权重属性熵的分类匿名算法(WECA)、Top-down以及IACK等三种算法的执行时间进行对比分析。

将准标识符属性个数设为8，参数值K={2,4,6,8,10}，三种算法在不同K值下的执行时间对比情况如图5所示。

图5 不同K值下的执行时间

从图5中可以看到，基于权重属性熵的分类匿名算法(WECA)、Top-down以及IACK等三种算法的执行时间均随着K值的增加而增加，而基于权重属性熵的分类匿名算法(WECA)的执行时间略高于其他两种算法。分析WECA算法执行时间略高的原因，是因为该算法为了平衡隐私保护与数据可用性，在其分类过程中需要同时考虑敏感属性的信息熵以及不同准标识符属性对敏感属性的分类重要程度，因此该算法执行时间略高是可以接受的。

以上实验综合可以得出，以上结论主要是对面向分类属性熵的隐私匿名方法进行研究，从而得出一种基于权重性熵的分类匿名算法分析，以上实验首先是引入问题，解析了目前大多数匿名模型和算法在保证数据隐私和可用性二者之间的一个平衡问题上单独的考虑了敏感属性的敏感度量对原始数据进行匿名的方法，并没有考虑到不同的标准标识符属性对敏感属性之间的重要程度的研究现状，然后引入了匿名要就及泛化层次，并且分析了隐私匿名数据损失度量，之后又重点分析并提出了权重属性熵分类匿名算法，引入了信息熵，通过对不同的标识符属性对敏感属性的分类重要程度的大小来构建分类匿名模型，接着构建了隐私分类匿名保护度量来获得更高数据的可用性和隐私安全性。最后证实了实验环境及数据集。

3 总结

综合上述几项实验的验证结果可知，相较于Top-down算法与IACK算法，本文所提出的本文所提出的基于权重属性熵的分类匿名算法(WECA)虽然执行时间略高，但是能够在保护数据隐私性的同时，兼顾分类精度问题，使数据可用性达到较高的水平。由此得出本文构建的隐私保护模型，在保护隐私安全的情况下，可提高数据的可用性，具有一定的借鉴价值。