支持语义扩展的动态多关键词密文排序检索

庞晓琼 严小龙 陈文俊 余本国 聂梦飞

摘 要：针对云存储环境下已有的动态多关键词密文排序检索方案不支持关键词语义扩展、不具备前向安全和后向安全的问题，提出一种支持语义检索且具备前向安全和后向安全的动态多关键词密文排序检索方案。该方案通过构建语义关系图实现查询关键词的语义扩展;使用树索引结构实现数据的检索和动态更新;利用向量空间模型实现多关键词排序搜索;基于安全K近邻算法对维度扩展后的索引和查询向量进行加密。安全性分析表明，该方案在已知密文模型下是安全的且具有动态更新时的前向安全和后向安全。效率分析及仿真实验结果表明，该方案在服务器检索效率方面优于目前同类型具有相同安全性或相同功能的方案。

关键词： 对称可搜索加密;多关键词排序检索;动态更新;语义扩展

中图分类号：TP309

文献标志码：A

文章编号：1001-9081（2019）04-1059-07

Abstract： Since existing dynamic multi-keyword ranked search schemes over encrypted data in cloud storage can not support semantic extension and do not have forward and backward security， a multi-keyword ranked search scheme over encrypted cloud data was proposed， which supported semantic search and achieved forward and backward security. The semantic extension of query keywords was achieved by constructing semantic relationship graph， the retrieval and dynamic update of data were achieved by use of tree-based index structure， the multi-keyword ranked search was achieved based on vector space model， and the extended index and query vectors were encrypted by using secure K-nearest neighbor algorithm. Security analysis indicates that the proposed scheme is secure under the known ciphertext model and achieves forward and backward security during dynamic update. Efficiency analysis and simulation experiments show that this scheme is superior to the same type schemes with the same security or function in server retrieval efficiency.

Key words： symmetric searchable encryption; multi-keyword ranked search; dynamic update; semantic extension

0 引言

隨着云计算的迅速发展，用户开始将数据迁移到云服务器，以避免繁琐的本地数据管理同时获得更加便捷的服务[1]，但近年来频繁发生的用户数据隐私泄露问题使得云安全问题受到人们的广泛关注。为保护敏感数据的隐私性，许多用户选择将数据以密文形式存储在云端[2]。但是，数据加密使得传统的明文关键词检索机制失效，如何对密文数据进行高效安全的检索成为亟待解决的问题。可搜索加密技术就是为了解决密文检索难题而提出的，该技术允许服务器在收到用户提交的关键词陷门后对密文直接进行检索，并将检索到的密文数据返回给用户;同时在检索过程中，云服务器无法根据密文文件以及用户提交的查询陷门推测出有关用户数据和检索词的有用信息。

可搜索加密主要分为对称可搜索加密和非对称可搜索加密[3]，本文研究前者。最初，大多数对称可搜索加密方案都仅支持单关键词检索[4-8]，然而实际情形中，用户为了更精确获取感兴趣的内容，往往输入多个关键词进行检索，并希望返回与输入关键词最相关的前K个文件。

为了满足此需求，近年来，支持多关键词排序检索的方案陆续被提出：2011年，Cao等[9]利用坐标匹配和向量内积技术首次提出了隐私保护的多关键词排序检索方案，该方案在构建文件索引向量和查询向量时未考虑不同关键词对文件的重要程度。2014年，Sun等[10]对Cao方案[9]作了改进，在构建索引向量和查询向量时引入了关键词权重，并通过向量余弦计算相关性提高了排序的精度。但以上工作都未考虑数据的动态更新。

现实情境中，数据拥有者需对其在云端的数据增加或删除。2014年，Sun等[11]以平衡二叉树作为索引提出了支持动态更新的多关键词排序检索方案。2017年，那海洋等[12]以B+树作为索引提出了支持动态更新的多关键词排序检索方案。但是，这两个工作都未考虑不可信云服务器可能会保存已经搜索过的检索或已经删除的文档，并利用先前的查询对新插入文档进行检索和利用新查询对已被删除文件进行检索，即方案未实现前向安全和后向安全。2014年，Yang等[13]提出了在动态更新时具有前向安全和后向安全的多关键词排序检索方案，但该方案采用倒排索引使得检索效率较低。

文献[9-13]的研究工作都是基于查询关键词的严格匹配，未考虑词语间的语义关系，这意味着返回的检索结果完全取决于用户的查询词是否与文档中预设的关键词严格匹配。然而在某些情况下，用户对相关领域知识了解不足，提交的关键词不能准确全面地表达用户的实际检索意图，造成检索结果不全面。针对此问题，2016年，Xia等[14]从语义角度考虑，通过构建语义关系图扩展用户的查询，构成新查询以更全面表达用户查询的语义信息，并提出了基于语义扩展的多关键词排序检索方案;但该方案不具备数据动态更新时的前向安全和后向安全。

本文针对支持语义扩展的多关键词密文排序检索技术展开研究，并提出一个支持语义扩展的动态多关键词密文排序对称可搜索加密方案，该方案同时具备前向和后向安全的数据动态更新功能，方案在已知密文模型下是安全的，且具有较高的检索效率。

1 系统模型与威胁模型

1.1 系统模型

系统模型包含三个实体，如图1所示。

1）数据拥有者（Data Owner， DO）。

DO加密文档、构建安全索引，将它们存储到云端;将用于检索的秘密信息通过安全信道发送给已认证用户。更新时，DO生成更新信息分别发送给云服务器和认证用户。

2）认证用户（Authenticated User， AU）。

AU生成查询陷门，并将陷门和希望返回的文档数K发送到云端。收到云端返回的前K个最相关的密文文档后对其进行解密。

3）云服务器（Cloud Server， CS）。

收到AU的檢索请求后，CS对加密索引进检索，并且依据相关性规则对检索结果排序，最后返回与检索请求最相关的前K个密文文档。数据更新方面，CS根据接收到的信息更新密文索引和密文文档集合。

1.2 威胁模型

方案中考虑如下敌手模型：收到用户的查询请求时，CS会遵守既定的规则，执行相关操作;但CS对存储在其上的数据是好奇的，并试图通过分析存储在其上的数据和接收到的信息获取尽可能多的用户数据隐私。在已知密文模型下CS可获得密文文档集合、密文索引、加密后的查询陷门。此外CS可能会保存已经搜索过的陷门或已删除的文档，能够利用以前的陷门对新插入的文档进行检索，或利用新陷门对已被删除的文件进行查询。

2 预备知识

2.1 符号定义

通过计算向量Dfj和Q的内积可得到fj与查询间的相关度。

2.3 语义关系图

2.4 语义扩展后的查询向量构建

AU生成待检索关键字集，并根据语义关系图生成语义扩展后的检索关键词集s，然后生成语义扩展后的查询向量Q，构建方法见算法GenSemanticExtentionVector（）。经语义扩展后的检索关键词集合s和文件fj的相关性分数计算如式（7）所示：

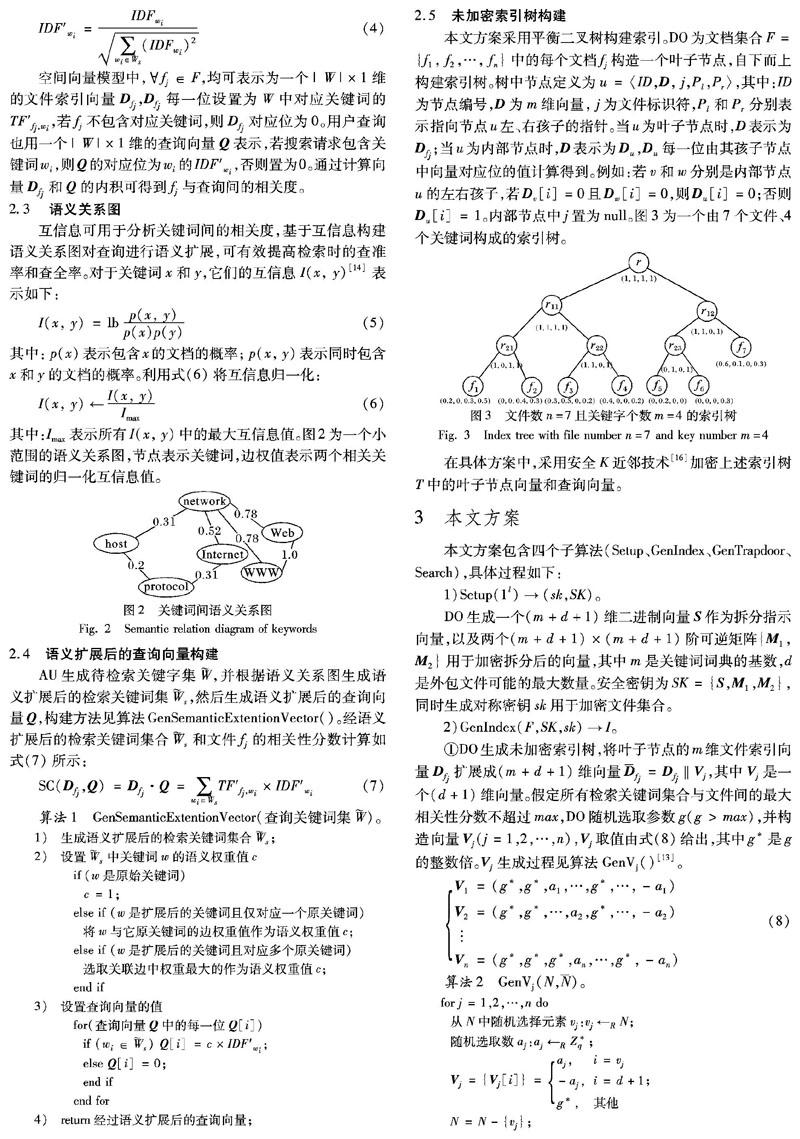
2.5 未加密索引树构建

在具体方案中，采用安全K近邻技术[16]加密上述索引树T中的叶子节点向量和查询向量。

3 本文方案

本文方案包含四个子算法（Setup、GenIndex、GenTrapdoor、Search），具体过程如下：

DO生成一个（m+d+1）维二进制向量S作为拆分指示向量，以及两个（m+d+1）×（m+d+1）阶可逆矩阵{M1，M2}用于加密拆分后的向量，其中m是关键词词典的基数，d是外包文件可能的最大数量。安全密钥为SK={S，M1，M2}，同时生成对称密钥sk用于加密文件集合。

收到AU的搜索请求后，CS对加密索引树I进行检索。若u为I中的一个内部节点，对于Ts中的每一项f（k1，wt），令at=λu[f（k1，wt）]，如果至少存在一个at使得Dec（g（k2，wt），at）=1，则以相同步骤继续检索u的左右孩子。当到达某一叶子节点时，计算该叶子节点的加密文件索引向量fj与AU加密的查询向量间的内积，有式（10）成立。

CS的检索过程见算法Search（）。

4 动态更新

4.1 插入和删除

算法UpdHelper（j，Ts，updtype）→{I′s，cj}由DO执行，以生成需要发送给CS的更新信息{I′s，cj}。输入参数j为文件标识符;updtype指明更新类型是删除还是插入;Ts为需要修改的树节点集合，一般为从更新节点到根节点路径上的所有节点。具体地：1）当updtype为删除时。若DO想删除文件fj，首先把存有fj信息的叶子节点删除，然后依据索引树构造规则对Ts中各节点的向量进行修改，得到新的节点集合T′s。例如，在图3中删除f3，Ts为{r22，r11，r}，对Ts中节点的向量修改后得到T′s，如r22的向量由（1，1，0，1）更新为（1，0，0，1），删除f3后的索引树如图4所示。接着通过伪随机函数对T′s中内部节点的向量加密，得到加密后的更新信息集合I′s。DO将{I′s，null}提交给CS，将vj加入集合N，同时将vj发送给AU，AU将vj从中删除。

5 安全性分析

5.1 索引和陷门的机密性

加密索引树叶子节点中fj的机密性基于安全K近邻技术。安全K近邻是一个不确定算法，即使两个文档的关键词集合相同，加密后的文件索引向量也不相同，更多有关安全K近邻算法加密数据的安全性分析可参考文献[16]。加密索引树每个内部节点中的哈希表λu，其第一项将关键词通过伪随机函数隐藏，第二项将内部节点对应向量位加密，只要保证伪随机函数密钥是安全的，仅由加密索引和密文文档集合，CS不能推断出内部节点向量Du。

陷门由{Ts，}构成，Ts由伪随机函数f（k1，·）和g（k2，·）隐藏检索关键词集合s得到，只要保证密钥k1和k2是安全的，CS就不能推断出s。由安全K近邻加密扩展后的查询向量得到，由于安全K近邻是一个不确定算法，即使两个检索关键词集合相同，对应的也不相同。

5.2 陷门的无关联性

本文方案采用二进制向量对文件索引向量和查询向量随机拆分，向量加密方法是一种不确定性加密，即使对前后两次相同的查询请求，也会生成不同的加密查询向量，从这个角度看实现了查询的无关联性。然而，由于相同的搜索请求会生成相同的Ts，检索时访问的内部节点和最终输出的加密文档是相同的;另外，即使被加密成了不同的向量，对于相同的查询请求，CS计算得到的相关性分数是相同的。基于以上两点，CS能够关联相同的查询请求，也只有在此种情况下，在已知密文模型下会泄露检索模式或访问模式。

5.3 前向安全和后向安全

前向安全性保证CS无法利用以前的查询陷门对新插入文档检索;后向安全性保证新陷门不能查询已删除文件。利用安全K近邻算法加密扩展后的文件索引向量和查询向量，本文方案保证了动态更新时的前向安全和后向安全。

从式（12）可看出，由于aj的随机性，当查询非法时，正确的相关性分数将被混淆。因此，本文方案实现了前向安全与后向安全。

5.4 功能及安全性比较

下面从功能和安全性方面将本文方案与文献[9-14]方案进行比较，结果如表1所示。仅本文方案同时具有语义检索功能和动态更新时的前向安全和后向安全。

文献[9-10，14]在已知背景知识模型下保证了陷门不可关联性，文献[11-13]和本文方案在已知密文模型下保证了陷门不可关联性。

6 效率分析及仿真实验

下面从加密索引构建、服务器检索和索引更新三个算法的计算开销方面，将本文方案与文献[13-14]方案进行对比，结果如表2所示。表2中：L表示构建每个内部节点的操作;X表示向量间点积运算（文献[13]方案和本文方案中表示两个（m+d+1）维向量间点积运算，文献[14]中表示两个m维向量间点积运算）;E和D分别表示加解密操作;M表示取模运算;R表示更新未加密向量的操作;B表示扩展文件索引向量的构建操作;t为s中的关键词数;m为关键词字典大小;d为外包文档集合中文件最大数量;θ为包含查询关键词的文档数。现实场景中，θ远小于文档集合基数n。

文献[13]方案采用倒排索引结构，本文方案和文献[14]方案为提高服务器检索效率，采用平衡二叉树作为索引。文献[13]方案在加密索引构建和更新索引方面效率最优，在检索时需计算2n次两个（m+d+1）维向量间点积运算。文献[14]方案在构建加密索引树时，利用安全K近邻技术对叶子节点和内部节点加密，因此在检索时，需对检索路径中的内部节点和叶子节点求相关性分数，最坏情况下，需做2θ lb n次两个m维向量间点积运算。本文方案在构建加密索引树时，仅利用安全K近邻技术对叶子节点加密，因此在检索时，仅需对叶子节点求相关性分数，对内部节点做解密操作，在最坏情况下，需做2θ次两个（m+d+1）维向量间点积运算。

接下来，对本文方案和文献[13-14]方案的服务器检索开销进行仿真实验及对比。实验中使用的数据集来源于英文文档集RFC（Request For Comments database）[18]，截止进行实验时RFC共包含8267篇文档，本文选用6000篇文档作为测试数据，利用全文检索工具Lucene对文档进行关键词提取，共得到9208个不同的关键词。实验环境：基于VMWare Workstation的虚拟机，宿主机CPU为Intel酷睿i7 6500U，虚拟机分配了1颗2核CPU、2GB内存，操作系统为Ubuntu 16.04 LTS 32位，对称加密算法为SM4，设置m=4000，d=6000，t=10。

为观察本文方案服务器检索开销与文档数n的关系，实验1中，固定θ分别为90和300，设置n=1000～6000（步长1000），实验结果如图6所示。可以看出，当θ确定时，检索时间随文档数增加呈对数增长，与性能分析结果一致。特别地，当θ=90时，n=1000，6000的检索时间分别为16.30ms和18.69ms;当θ=300时，n=1000，6000的检索时间分别为51.13ms和59.49ms。

为观察本文方案服务器检索开销与θ的关系，实验2中，固定文档数n为2000，设置θ从50～300，步长50，实验结果如图7所示。可以看出，检索时间随θ的增加呈线性增长，与性能分析结果一致。特别地，当θ=50，300时，检索时间分别为9.37ms和54.13ms。

文献[13]方案的检索开销与θ无关，文献[14]方案和本文方案的检索开销与θ相关，为对三者进行比较，实验3中，固定θ分别为90和300，设置文档数n从1000～6000，步长1000，实验结果如图8所示。可以看出：1）文献[13]方案的检索时间随着n的增加基本呈线性增长;2）文献[14]方案在θ=90的检索开销略低于文献[13]方案，在θ=300时显著高于文献[13]方案;3）本文方案在θ=90与θ=300时的检索开销均明顯低于文献[13-14]方案，这是因为文献[13]方案检索时需要计算2n次两个（m+d+1）维向量间的点积运算，文献[14]方案需做2θ lb n次两个m维向量间点积运算，本文方案只需进行2θ次两个（m+d+1）维向量的点积运算（θn），当然本文方案还需进行tθ（lb n-1）次一个1bit的解密操作，但1bit解密操作的速度非常快，因此在检索效率方面本文方案优于文献[13-14]方案。

7 结语

本文提出了一个支持语义扩展的动态多关键词密文排序检索方案，对方案的安全性进行了分析，并与现有的多关键词密文排序检索方案进行了功能和安全性比较，实验结果表明仅本文方案同时具有语义检索功能和动态更新时的前向安全和后向安全。此外，对方案的效率进行了理论分析和仿真实验，实验结果表明本文方案在加密索引构建和索引更新效率方面弱于文献[13]方案，但在服务器检索效率方面显著优于具有相同安全性的文献[13]方案和具有语义扩展功能的文献[14]方案。

参考文献（References）

[1] 张玉清， 王晓菲， 刘雪峰， 等.云计算环境安全综述[J]. 软件学报， 2016， 27（6）： 1328-1348. （ZHANG Y Q， WANG X F， LIU X F， et al. Survey on cloud computing security[J]. Journal of Software， 2016， 27（6）： 1328-1348.）

[2] 魏凱敏， 翁健， 任奎. 大数据安全保护技术综述[J]. 网络与信息安全学报， 2016， 2（4）： 1-11. （WEI K M， WENG J， REN K. Data security and protection techniques in big data： a survey[J]. Chinese Journal of Network and Information Security， 2016， 2（4）： 1-11.）

[3] 董晓蕾， 周俊， 曹珍富， 等.可搜索加密研究进展[J]. 计算机研究与发展， 2017， 54（10）： 2107-2120. （DONG X L， ZHOU J， CAO Z F， et al. Research advances on secure searchable encryption[J]. Journal of Computer Research and Development， 2017， 54（10）： 2107-2120.）

[4] SONG X D， WAGNER D， PERRIG A. Practical techniques for searching on encrypted data[C]// Proceedings of the 2000 IEEE Symposium on Security and Privacy. Piscataway， NJ： IEEE， 2000： 44-55.

[5] GOH E. Secure indexes[EB/OL]. [2018-05-10]. http：//crypto.stanford.edu/-eujin/papers/secureindex.

[6] CHANG Y C， MITZENMACHER M. Privacy preserving keyword searches on remote encrypted data[C]// ACNS 2005： Proceedings of the 2005 Applied Cryptography and Network Security， LNCS 3531. Berlin： Springer， 2005： 442-455.

[7] CURTMOLA R， GARAY J， KAMARA S， et al. Searchable symmetric encryption： improved definitions and efficient constructions[C]// CCS 2006： Proceedings of the 13th ACM Conference on Computer and Communications Security. New York： ACM， 2006： 79-88.

[8] WANG C， CAO N， REN K， et al. Enabling secure and efficient ranked keyword search over outsourced cloud data[J]. IEEE Transactions on Parallel & Distributed Systems， 2011， 23（23）： 1467-1479.

[9] CAO N，  WANG C， LI M， et al. Privacy-preserving multi-keyword ranked search over encrypted cloud data[C]// Proceedings of the 30th IEEE International Conference on Computer Communications.  Piscataway， NJ： IEEE， 2011： 829-837.

[10] SUN W， WANG B， CAO N， et al. Privacy-preserving multi-keyword text search in the cloud supporting similarity-based ranking[J]. IEEE Transactions on Parallel & Distributed Systems， 2014， 25（11）： 3025-3035.

[11] SUN X， ZHOU L， FU Z， et al. Privacy-preserving multi-keyword ranked search over encrypted cloud data supporting dynamic update[J]. International Journal of Security & Its Applications， 2014， 8（6）： 1-16.

[12] 那海洋， 杨庚， 束晓伟. 基于B+树的多关键字密文排序检索方法[J]. 计算机科学， 2017， 44（1）： 149-154. （NA H Y， YANG G， SHU X W. Multi-keyword ranked search method based on B+tree[J]. Computer Science， 2017， 44（1）： 149-154.）

[13] YANG Y， LI H， LIU W， et al. Secure dynamic searchable symmetric encryption with constant document update cost[C]// Proceedings of the 2014 IEEE Global Communications Conference. Piscataway， NJ： IEEE， 2014： 775-780.

[14] XIA Z， CHEN L， SUN X， et al. A multi-keyword ranked search over encrypted cloud data supporting semantic extension[J]. International Journal of Multimedia & Ubiquitous Engineering， 2016， 11（8）： 107-120.

[15] WITTEN I H， MOFFAT A， BELL T C. Managing Gigabytes： Compressing and Indexing Documents and Images[M]. San Francisco： Morgan Kaufmann Publishers， 1999： 180-188.

[16] WONG W K， CHEUNG W L， KAO B， et al. Secure kNN computation on encrypted databases[C]// SIGMOD 2009： Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data. New York： ACM， 2009： 139-152.

[17] CORMEN T H， LEISERSON C E， RIVEST R L， et al. Introduction to Algorithms[M]. 3rd ed. Cambridge， MA： MIT Press， 2009： 256-261.

[18] IAB， IETF. Request for comments available[DB/OL]. [2018-05-10]. https：//www.rfc-editor.org/retrieve/bulk/.