融入二维码信息的自适应蒙特卡洛定位算法

胡章芳 曾林全 罗元 罗鑫 赵立明

摘 要：蒙特卡洛定位（MCL）算法存在计算量大、定位精度差的问题，由于二维码具有携带信息的多样性、二维码识别的方便性与易用性的特点，提出一种融入二维码信息的自适应蒙特卡洛定位算法。首先，利用二维码提供的绝对位置信息修正里程计模型的累计误差后进行采样;然后，采用激光传感器提供的观测模型确定粒子的重要性权重;最后，因为重采样部分采用固定样本集会导致大计算量，所以利用Kullback-Leibler距离（KLD）进行重采样，根据粒子在状态空间的分布情况自适应调整下一次迭代所需粒子数，从而减小计算量。基于移动机器人进行的实验结果表明，改进算法与传统蒙特卡洛算法相比定位精度提高了15.09%，时间缩短了15.28%。

关键词：蒙特卡洛定位;里程计运动模型;观测模型;二维码;Kullback-Leibler距离采样

中图分类号：TP242.6

文献标志码：A

文章编号：1001-9081（2019）04-0989-05

Abstract： Monte Carlo Localization （MCL） algorithm has many problems such as large computation and poor positioning accuracy. Because of the diversity of information carried by two-dimensional code and usability and convenience of two-dimensional code recognition， an adaptive MCL algorithm integrated with two-dimensional code information was proposed. Firstly， the cumulative error of odometer model was corrected by absolute position information provided by two-dimensional code and then sampling was performed. Sencondly， the measurement model provided by laser sensor was used to determine the importance weights of the particles. Finally， as fixed sample set used in the resampling part caused large computation， Kullback-Leibler Distance （KLD） was utilized in resampling to reduce the computation by adaptively adjusting the number of particles required for the next iteration according to the distribution of particles in state space. Experimental result on the mobile robot show that the proposed algorithm improves the localization accuracy by 15.09% and reduces the localization time by 15.28% compared to traditional Monte-Carlo algorithm.

Key words： Monte-Carlo Localization （MCL）; odometer motion model; measurement model; two-dimensional coding; Kullback-Leibler Distance （KLD） sampling

0 引言

在環境地图已知的前提下，移动机器人根据环境感知和自身运动确定其在环境中的位姿问题称为定位问题。蒙特卡洛定位（Monte Carlo Localization， MCL）算法[1]以运动模型采样，并结合观测模型评估每个粒子的重要性权重，得到系统状态的后验信度分布。

该算法成功应用于移动机器人领域，适用于局部定位和全局定位两类问题。里程计运动模型通过整合车轮上的光电编码器信息，进而获得机器人相对于上一采样时刻位姿的相对差，在固定的时间间隔可进行位姿估计。但是由于漂移或打滑等因素的影响，导致运动模型的精度随时间的增大而下降，MCL算法的先验分布依赖于里程计运动模型的精度，若预测粒子分布与实际位姿相差太大易导致定位定位误差增大;另外，重采样后粒子会产生退化效应，粒子多样性降低，固定大样本粒子会导致计算资源浪费，因此学者们一直在研究如何解决这两类问题。Borenstein等[2]在20世纪90年代就将里程计误差分为系统误差和非系统误差两个部分，并提出了一种里程计标定方法UMBmark消除系统误差对里程计精度影响，机器人按预定轨迹运动几次便可标定出差动轮模型参数。Yap等[3]利用最大期望（Expectation Maximization， EM）算法并结合环境建图来同时计算里程计运动模型和激光器观测模型的参数，最后实现了在线自适应标定。Alhashimi等[4]改进蒙特卡洛算法的观测模型，通过设置的阈值来确定粒子样本集合的大小，有效减小了计算量。黄露等[5]设计人工路标并建立了路标库来修正里程计的累计误差;

但是由于人工路标设计复杂且路标库建立需要大量数据导致定位精度低、计算量大，而且准确性也无法满足要求。

因此，本文提出一种融入二维码信息的自适应蒙特卡洛定位算法（Adaptive MCL algorithm Integrated with two-dimensional code information， I-AMCL），在采样过程中融入二维码携带的绝对位置信息，激光传感器信息用于更新粒子权重，并采用Kullback-Leibler距离（Kullback-Leibler Distance， KLD）[6]重采样，根据采样在状态空间的近似分布的统计界限来确定粒子数。最后，通过实验验证在保证最优位姿估计和稳定性不受影响的情况下，本文算法减小计算量，并提高定位精度。

假设当前的粒子群St只依赖于上一时刻的粒子群St-1，初始置信度bel（x0）由先验分布 p（x0）随机产生的m个这样的粒子得到，并为每个粒子分配相同的重要性因子m-1。该算法第3）行利用运动模型进行采样，以当前置信度为起点分配粒子;第4）行观测模型对每个粒子的权重进行更新;第5）～11）行根据粒子权重重采样得到新的粒子群，并不断迭代。

2 本文算法

将视觉传感器提供的二维码的绝对位置信息融入到里程计运动模型中，可修正里程计的累计误差;而每次迭代过程中的重采样会带来繁重的计算量，

因此本文提出一种融入二维码信息的自适应蒙特卡洛定位算法（I-AMCL），以提高定位精度，减少计算量。

2.1 运动模型采样

2.1.1 里程计运动模型

里程计使用的机器人内部坐标和全局世界坐标之间不存在固定的坐标变换，因此里程计模型的建立需要机器人内部编码器观测的相对运动信息。在时间间隔（t-1，t]内，给定运动信息ut为：

这就是里程计误差，在机器人定位过程中容易导致定位误差。

2.1.2 二维码信息

由于直接将视觉传感器识别的离散坐标融入里程计模型误差较大，所以应提供机器人位置的直接观测信息，因此需要计算出二维码中心点在车体坐标系中的精确位置[7-9]。

为了计算三维空间中物体的几何信息，需要对摄像机进行标定，由此得出摄像机的内参数矩阵A和外参数矩陣R，确定摄像机相对于世界坐标系的方位。

由于摄像头焦距不为0，有矩阵A和R可逆。可通过下式计算拍摄照片中的像素点在车体坐标系中的实际坐标。

当知道二维码中心在图像中的坐标（uc，vc），就可以计算出其在车体坐标系中的坐标（Xc，Yc，Zc），因此本文使用一个简单易用的二维码识别库（Zbar库），获取DM码三个位置探测图形在图像中的坐标（u1，v1）、（u2，v2）、（u3，v3）。

二维码中心位于对角探测图形连线中心上。由于已知探测图形的位置，可计算二维码的中心（uc，vc）在图形中的坐标为：（uc，vc）=（u1+u32，v1+v32）（14）

将（uc，vc）代入就可以获取二维码在车体坐标系中的坐标xc=（Xc，Yc，Zc）。

2.1.3 融入二维码信息的采样

运动模型采样将初始姿态xt-1、里程计读数ut和相机读数xc作为输入，输出一个随机xt服从p（xtut，xt-1）的分布。机器人在运动过程中没有扫描到二维码时，首先由式（2）～（8）推测一个位姿xt，当相机获取二维码信息，与此时里程计采样输出的位姿xt进行比较，两者误差大于临界值τ，则采样算法输出的值为二维码坐标的绝对值xc，并令当前时刻的位姿xt为二维码信息提供的位姿，继续进行采样直到扫描下一个二维码。

2.2 激光传感器的似然域

其中：xt是机器人的位姿;zt是t时刻的观测;M是环境地图。假设每个观测束噪声之间独立。

机器人在定位时需将传感器扫描的终点zt映射到地图的全局坐标空间。令xt=（x， y，θ）T表示机器人在t时刻的位姿。用（xk，sens， yk，sens）T表示安装在机器人上的激光传感器局部坐标系统的位置，用θk，sens表示激光光束相对于机器人航向的角度。观测zkt的终点经过三角变换映射到全局坐标系：

传感器检测到障碍物时这些坐标才具有意义，因此最大距离读数将被丢弃。

三个参数zhit、zrand和zmax进行加权平均混合，并且zhit+zrand+zmax=1。

2.3 基于KLD的重采样

用于表示置信度的采样集的大小对粒子滤波器的效率影响程度很大。为了使移动机器人能够处理全局定位和位置跟踪问题，必须选择大样本集合来避免采样消耗引起的发散，若采用固定大小的样本集合，会导致非常大的计算量。KLD采样能随时间自适应改变粒子数。

KLD采样对每次粒子滤波迭代都以概率1-δ确定样本数，使得真实的后验分布与基于采样的近似分布之间的误差小于ε，由此确定重采样样本集合的大小[10-11]。当粒子数m满足一定值时，可以保证概率的真实值与估计值之间的K-L距离小于阈值ε，此时m的值为：

2.4 融入二维码信息的自适应MCL算法

与蒙特卡洛算法相比，本文算法I-AMCL除了将t-1时刻的采样集合St-1、地图M和最新的控制ut及观测zkt作为输入，KLD采样还把一个加权后采样集合和二维码提供的全局坐标信息xc与临界值τ作为输入，且要求输入统计误差界限ε和δ。

算法I-AMCL在满足第27）行统计界限之前，KLD采样将一直产生粒子。这个界限基于粒子所覆盖的状态空间的体积，粒子覆盖的体积由覆盖在三维状态空间的位来衡量，直方图H的位有两种状态：空或被一个粒子占据（第3）～5）行），这个粒子是从St-1样本集合中提取出来的（第7）行）。基于这个粒子，一个新粒子被预测、加权，并插入到新采样集合，这里预测采用的是二维码修正过的里程计模型（第8）～14）行），加权采用的激光传感器的似然域（第15）～21）行）。h是至少填充了一个粒子的直方图的位数，如果新产生的粒子落入直方图的一个空位中，那么非空位数目h是增加的，并且该位被标记为非空（第22～30）行）。本文算法I-AMCL如算法2所示。

3 实验与结果分析

3.1 仿真研究

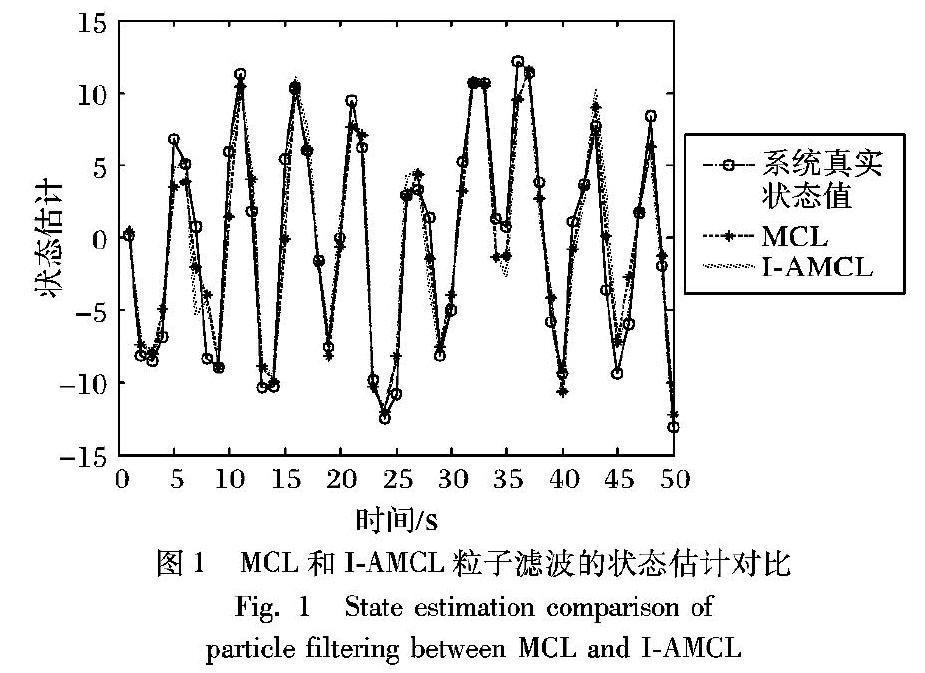
首先通过仿真实验进行研究。使用Matlab 2012a在计算机上进行仿真，I-AMCL参数设置如下：c=0.7，ε=0.1，τ=0.01，δ=0.01，实验所用初始粒子数为1000。从图1可看出，I-AMCL与真实状态值更接近，有相近的收敛速度，由此说明本文算法估计精度更高。

3.2 系统实现

3.2.1 实验平台

为验证本文算法I-AMCL的有效性，采用如图2所示的室内移动机器人来进行。

在仓库物流场景中，机器人根据订单任务在粘贴有二维码的位置进行装货卸货，该机器人采用光电编码器进行相对位置观测，并配有CPU为1.86GHz运行内存为2GB的笔记本电脑，机器人的运动速度为V=0.2m/s，采用灰度摄像头，在1280×1024的分辨率下图像传输速度达100fps。为保证旋转过程中二维码始终位于摄像头视野之内，并给摄像头提供稳定的照明，本文将摄像头安装在驱动轮之间，使摄像头的光心和机器人的旋转中心重合。运行时，安装LED阵列在车辆底部，可以提供稳定照明。

高速二维码的识别对攝像头的拍摄帧率、曝光时间等都有要求。由于摄像头安装在车底，距离地面的高度有限制，实测其视野的边长为0.15m。本文使用的二维码为DM码，用于存储坐标信息，坐标信息计算方法为，利用精度为0.1cm的卷尺测量二维码之间的距离，并通过几何关系求出坐标（X，Y），航向角θ值由机器人正方向和读取二维码的方向之间的夹角确定。然后利用二维码的位置探测图形来确认机器人和二维码间的相对坐标。因此，可利用网页工具或二维码批量生成工具等，将实际的坐标信息/坐标编号存入到DM码中，由此，当机器人行驶到二维码上方时，可以通过扫描二维码来确认自身的当前坐标。二维码粘贴示例如图3所示。

3.2.2 实验结果分析

利用机器人操作系统（Robot Operating System， ROS）中的gmapping节点构建室内环境地图[12]，初始位置已知，MCL和I-AMCL的初始粒子数都设置为1000，其相关参数设置同步仿真实验。完成机器人在先验地图中的精确定位。

机器人从A点到B点的规划路径如图4（a）所示（其中①～④表示二维码粘贴位置）。图4（b）～（e）表示机器人在运动过程中通过二维码粘贴位置时的粒子变化情况，中心大圆点表示机器人，周围的小点表示粒子，箭头表示机器人移动方向。从图4可看出移动机器人在利用I-AMCL进行定位时，在初始位置，粒子数较多并分布在机器人周围，随着机器人运动，观测值和控制值在不断矫正机器人的位姿，其定位所需粒子数在不断减少，且机器人在二维码粘贴位置的定位精度较高。

图5为两种算法的粒子数随机器人运动距离的变化情况，进一步说明MCL采用固定粒子数，而I-AMCL在机器人运动过程中可根据自由空间状态来实时调整定位所需粒子数，结合二维码位姿信息和激光传感器的观测信息，移动机器人定位所需粒子数为110左右。

如图6所示的室内环境为重庆邮电大学自动化学院一楼。为模拟仓库物流环境，将二维码粘贴在①～⑥位置，如图6（a）所示。实验过程中6个二维码均能被快速识别，分别记录机器人采用两种算法的运动轨迹的实测值。定位数据分析对比如图6所示：图6（b）为MCL算法定位路径，与规划路径相比误差明显;图6（c）为I-AMCL定位路径，可以明显看出定位精度得到了明显的提高，使得定位路径明显趋近于规划路径，整个导航系统的误差大幅度降低。

表1对比了两种定位算法的性能，可以说明本文算法I-AMCL有更精确的定位，可根据机器人的状态实时调整采样粒子数达到提高计算效率的目的，实现机器人室内导航。

4 结语

本文提出了一种融入二维码信息的自适应蒙特卡洛定位（I-AMCL）算法，利用摄像机提供的二维码信息修正里程计模型后再采样，激光传感器提供的观测模型用以确定粒子的重要性权重;并采用KLD重采样调整所需粒子数，减小了计算量同时提高了定位精度;最后通过仿真和实验验证了本文算法的可行性。但是，本文人为地改变了部分环境地图信息，导致机器人的起始点必须在二维码正上方，在一定程度上缺乏灵活性。

参考文献（References）

[1] THRUN S， FOX D， BURGARD W， et al. Robust Monte Carlo localization for mobile robots[J]. Artificial Intelligence， 2001， 128（1/2）： 99-141.

[2] BORENSTEIN J， FENG L. Measurement and correction of systematic odometry errors in mobile robots[J]. IEEE Transactions on Robotics and Automation， 1997， 12（6）： 869-880.

[3] YAP T N， SHELTON C R. Simultaneous learning of motion and sensor model parameters for mobile robots[C]// Proceedings of the 2008 IEEE International Conference on Robotics and Automation. Piscataway， NJ： IEEE， 2008： 2091-2097.

[4] ALHASHIMIl A W， HOSTETTLER R， GUSTAFSSON T. An improvement in the observation model for Monte Carlo localization[C]// Proceedings of the 2014 11th International Conference on Informatics in Control， Automation and Robotics. Piscataway， NJ： IEEE， 2014： 498-505.

[5] 黄露， 朱明. 单目视觉人工路标辅助的移动机器人导航方法[J]. 计算机系统应用， 2018， 27（1）： 106-112. （HUANG L， ZHU M. Mobile robot navigation algorithm assisted by monocular vision artificial road sign[J]. Computer Systems & Applications， 2018， 27（1）： 106-112.）

[6] ZHOU T， PENG D， XU C， et al. An adaptive particle filter based on Kullback-Leibler distance for underwater terrain aided navigation with multi-beam sonar[J]. IET Radar， Sonar & Navigation， 2018， 12（4）： 433-441.

[7] 尚明超， 杨斌， 张翠芳. 二维码修正EKF-SLAM定位的室内无人驾驶小车[J]. 单片机与嵌入式系统应用， 2017， 17（7）： 63-66. （SHANG M C， YANG B， ZHANG C F. Indoor driverless car with EKF-SLAM localization modified by QR code[J]. Microcontroller and Embedded System Applications， 2017， 17（7）： 63-66.）

[8] LI Z Q， HUANG J D. Study on the use of QR codes as landmarks for indoor positioning： preliminary results[C]// Proceedings of the 2018 IEEE/ION Position， Location and Navigation Symposium. Piscataway， NJ： IEEE， 2018： 1270-1276.

[9] TRUC N T， KIM Y T. Navigation method of the transportation robot using fuzzy line tracking and QR code recognition[J]. International Journal of humanoid Robotics， 2016， 14（2）： 456-460.

[10] WANG F， LIN Y. Improving particle filter with a new sampling strategy[C]// Proceedings of the 2009 4th International Conference on Computer Science and Convergence Information Technology. Piscataway， NJ： IEEE， 2009： 408-412.

[11] WANG F， ZHAO Q， ZHANG Y， et al. Particle filtering with multi proposal distributions[J]. International Journal of Communications Network & System Sciences， 2008， 1（1）： 22-28.

[12] 張建伟， 张立新， 胡颖， 等. 开源机器人操作系统——ROS[M]. 北京： 科学出版社， 2012： 1-6. （ZHANG J W， ZHANG L X， HU Y， et al. The Open Source Robot Operating System — ROS[M]. Beijing： Science Press， 2012： 1-6.）