实测不平整激励下跑道平整度评价方法对比

凌颖琦，刘诗福，林 盛，吴 磊，宾雪阳

（1.同济大学浙江学院交通运输工程系，浙江 嘉兴 314051；2.同济大学道路与交通工程教育部重点实验室，上海 201804；3.河北建设集团股份有限公司空港分公司，北京 100621）

平整度是机场跑道的一项重要性能，不平整的跑道会造成飞机颠簸，严重时会影响飞行员对飞机的控制，降低旅客的舒适度。此外，还会对道面产生极大的冲击力，从而加速道面损坏。附加的振动作用也会加剧飞机起落架等构件的磨损，威胁飞行安全。

《民用机场道面评价管理技术规范（MH/T 5024-2009）》规定，中国民用机场跑道主要通过车载式激光平整度仪获取道面国际平整度指数（IRI,international roughness index）指标，通过对IRI 的阈值划分来评价跑道平整度的伪劣状况[1]。多数研究表明，由于飞机胎压、起落架构型及荷载作用等特性与汽车存在一定的差异，理论上IRI 只适用于公路路面而不适用于机场道面[2-3]。蔡宛彤等[4]通过ADAMS 建立飞机仿真模型并分析修正了跑道平整度评价标准。凌建明等[5]从波长的敏感性出发，发现IRI 指标不适用于跑道平整度的评价。程国勇等[6]指出当前IRI 在机场跑道平整度评价中主要存在两个缺点：①其所表征的平整度范围与飞机尺度不协调；②无法衡量机轮下道面不平整情况所产生的耦合效果。波音公司于20 世纪70年代开展跑道平整度评价体系的研究[7]，提出的波音平整度指数（BBI,Boeing bump index）被美国联邦航空管理局（FAA）采用，并作为机场道面管理系统的重要指标。凌建明等[8]认为应将BBI 指标纳入跑道平整度评价体系，形成同时以IRI 和BBI 作为跑道平整度评价指标的格局，但由于缺乏实测跑道不平整数据，未进一步分析并给出跑道平整度实际评价时以哪个指标为主。目前针对BBI 的适用性研究不多，且多数都是利用仿真道面进行分析[9]。

因此，首先阐述新版道面评价规范中关于机场跑道平整度评价指标的计算方法以及相应评价标准；然后建立飞机滑跑动力学响应模型，提出竖向加速度均方根作为跑道平整度的评价指标；最后以实测跑道不平整激励为基础，基于Matlab 开发跑道平整度评价方法对比与分析流程，多维度探究IRI 和BBI 指标与飞机滑跑动力响应特性的关系，研究结果可作为修订规范的完善和补充。

1 跑道平整度评价方法

1.1 国际平整度指数

1）IRI 模型

IRI 是通过求解1/4 车模型的振动方程而得出的平整度指标。测试时，规定测试车辆以规定速度（80 km/h）行驶在路面上，将行驶距离内悬挂系统的累积竖向位移量作为IRI 值。其计算原理[10]如图1所示。

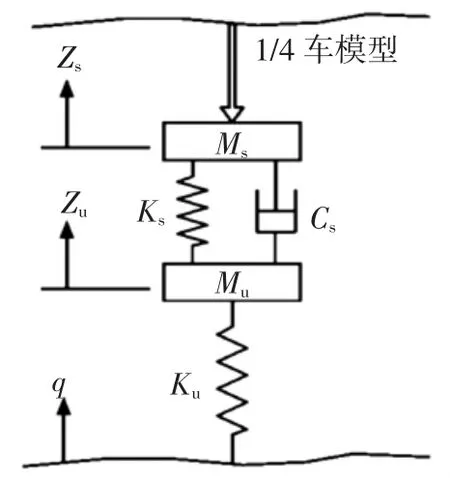
图1 IRI 计算模型Fig.1 IRI calculating model

其中：q 为不平整激励；Ks为簧载质量刚度系数；Ku为非簧载质量刚度系数；Cs为簧载质量阻尼系数。IRI为单位距离内车辆簧载质量Ms和非簧载质量Mu的累计相对位移，即

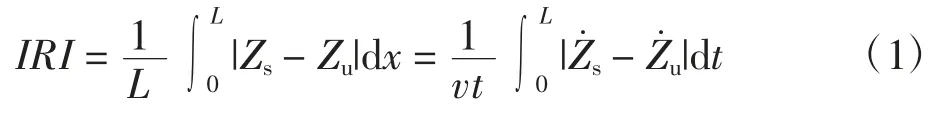
其中：L 为路段长度；Zs、Zu分别为Ms和Mu的竖向位移；v 为行驶速度；x 为纵向位移；t 为行驶时间。

2）IRI 评价标准

IRI 可通过激光平整度仪自动测试并计算，测试时应沿各区域的轮迹带布设侧线。以调查区域内的IRI算术平均值进行分段评价，跑道平整度的评价标准为好（IRI ＜2.0 m/km）、中（2.0 m/km≤IRI≤3.0 m/km）、差（IRI ＞3.0 m/km）。

1.2 波音平整度指数

为解决功率谱密度方法难以区分小振幅多波动与大振幅少波动的问题，波音公司于20 世纪70年代开始机场跑道平整度的相关研究。基于波音飞机滑行的疲劳损伤实验，提出基于最大隆起高度（bump height）和隆起长度（bump length）两者关系的评价指标[7]。FAA 在此基础上提出BBI 计算方法及评价标准[10]。

1.2.1 BBI 计算流程

1）对于纵断面采样点，计算所有不同长度“直尺”下的隆起高度和隆起长度；

2）计算不同隆起长度对应的隆起高度允许值；

3）对不同隆起长度计算实际隆起高度与允许值的比值，其中最大比值为断面采样点的BBI 值；

4）对所有纵断面采样点重复以上步骤。

1.2.2 BBI 评价标准

用于计算BBI 的道面纵断面相对高程宜采用纵断面高程自动采集设备，以调查区域内BBI 的算术平均值进行分段评价，评价标准为可接受区（BBI ＜1.0）、超过区（1.0≤BBI≤1.25）、不可接受区（BBI ＞1.25）。

BBI 评价标准主要分成3 个区域，如图2所示。

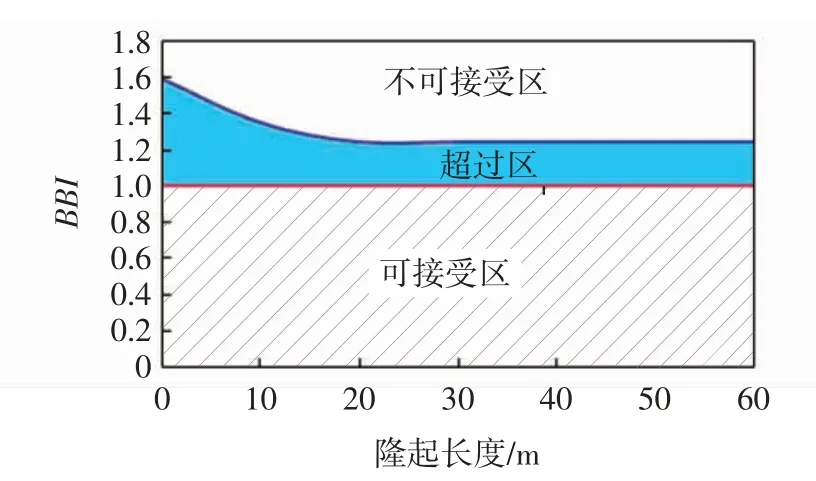
图2 BBI 评价标准Fig.2 BBI evaluation standard

1）可接受区 满足乘客舒适度要求及不干扰飞机驾驶员对仪器读数，不需要进行维护；

2）超过区 道面隆起位于超过区范围，道面的不平整对飞行员与乘客造成明显的不适感，严重影响仪器读数和操作，并对起落架产生过载影响，需要及时维修；

3）不可接受区 不可接受区的跑道将严重影响飞机起落架疲劳寿命，需要立即关闭。

2 飞机滑行动力响应分析

跑道的服务对象为飞机，跑道平整度直接影响滑跑飞机的振动程度。因此，可用飞机滑行过程中的重心竖向加速度表征跑道平整度状况。

2.1 计算模型

建立飞机滑跑动力学模型，同时考虑飞机随机振动下的竖向运动、俯仰转动和侧倾转动，如图3所示。

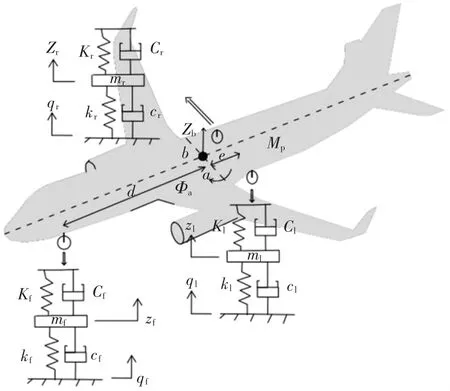
图3 飞机滑跑动力学模型Fig.3 Aircraft taxiing dynamical model

根据达朗贝尔原理，以飞机平衡位置为坐标原点，在不平整道面的激励下簧载质量的竖向振动平衡方程为

其中：Mp为飞机模型的簧载质量；Kf、Kl、Kr分别为前、左后、右后起落架簧载质量的刚度系数；Cf、Cl、Cr分别为前、左后、右后起落架簧载质量的阻尼系数；d、e 分别为前后起落架到飞机横轴的垂直距离，a、b 分别为左后、右后起落架到飞机纵轴的垂直距离；Z 为飞机簧载质量的竖向位移；Φ 为簧载质量的俯仰转动位移；Ψ 为簧载质量的侧倾转动位移；zf为前起落架非簧载质量的竖向位移；zr为右后起落架非簧载质量的竖向位移；zl为左后起落架非簧载质量的竖向位移。

簧载质量Mp的俯仰转动的平衡方程为

其中：Ix为飞机模型绕飞机横轴（x 轴）的转动惯量。簧载质量的侧倾转动平衡方程为

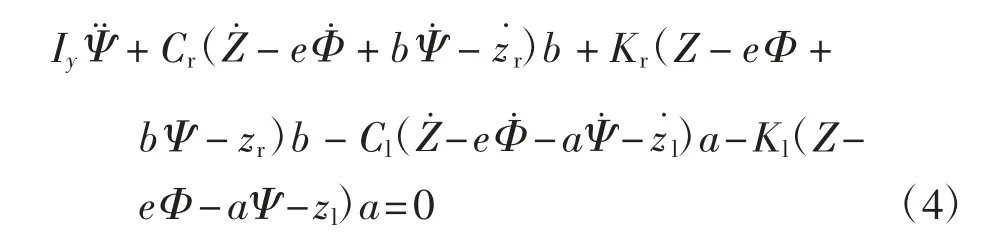
其中：Iy为飞机模型绕飞机纵轴（y 轴）的转动惯量。

根据竖直方向的力平衡，前起落架非簧载质量的振动平衡方程为

其中：mf为前起落架非簧载质量；kf为前起落架非簧载质量的刚度系数；cf为前起落架非簧载质量的阻尼系数；qf为前起落架非簧载质量的不平整激励。

左后起落架非簧载质量的振动平衡方程为

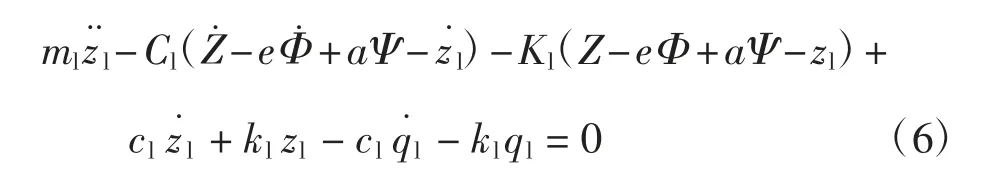
其中：ml为左后起落架非簧载质量；kl为左后起落架非簧载质量的刚度系数；cl为左后起落架非簧载质量的阻尼系数；ql为左后起落架非簧载质量的不平整激励。

右后起落架非簧载质量的振动平衡方程为

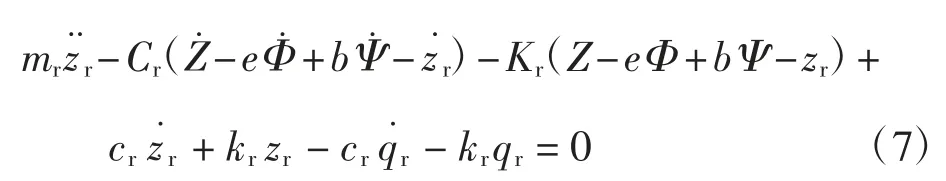
其中：mr分别为右后起落架非簧载质量；kr为右后起落架非簧载质量的刚度系数；cr为右后起落架非簧载质量的阻尼系数；qr为右后起落架非簧载质量的不平整激励。

2.2 加速度均方根

对于矢量的竖向加速度，由于机场道面的纵断面连续平整度序列可看作是一种服从高斯概率分布且零均值的随机场，飞机滑跑在随机场道面条件下的竖向加速度均值趋于0。根据统计学原理，均值为0 的数列加速度均方根值与标准差相同，即

其中：N 为采集的点数；aj为飞机第j 个样本点的竖向加速度数值。乘客舒适性一般以0.4 g 作为加速度均方根RMS 的阈值。

3 试验分析

3.1 实测跑道不平整激励

目前常用机型的主轮距在15 m 以下，考虑到飞机滑跑的轮迹偏移，横向采集以中心线为对称的10 m范围数据，间隔为1 m，共21 条测线；纵向通过车载式激光平整度仪采集间隔为0.25 m、精度为0.1 mm 的平整度数据。以华东某2 500 m 长的4D 机场跑道为例，采集三维平整度数据如图4所示，其中跑道横线10 m处表示跑道的中心线。

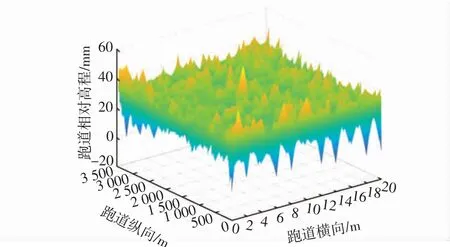
图4 实测三维跑道平整度数据Fig.4 3D Runway smoothness of measured data

3.2 基于Matlab 的仿真分析流程

Matlab 是一款用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言软件。利用Matlab 软件开发实测不平整激励下跑道平整度评价方法对比和分析流程，如图5所示。对比和分析流程包括：①输入端包括采集的跑道三维不平整相对高程数据、评价指标收集的间隔、仿真机型以及仿真速度；②在Matlab 核心主程序中，分别计算1/4 车模型的响应、遍历BBI 指标规定的每种波长以及仿真飞机重心加速度响应；③输出端包括IRI 分布、BBI 分布以及飞机振动响应分布；④分析端包括BBI、IRI 评价指标和飞机振动响应分布的相关性分析以及适应性分析。

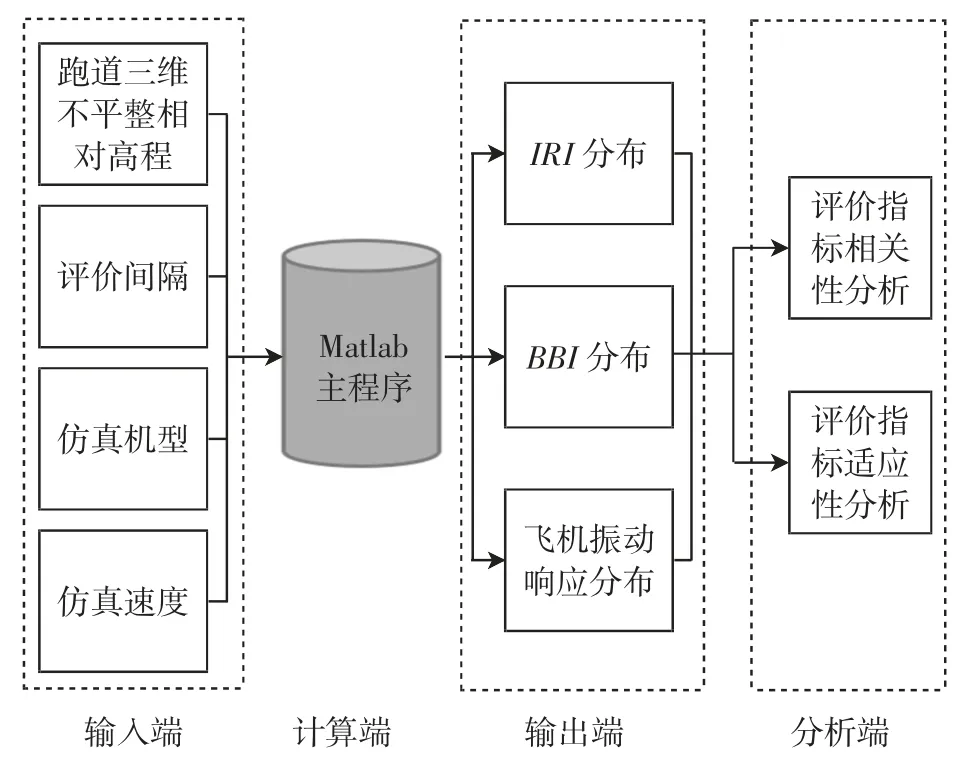
图5 跑道平整度评价方法对比和分析流程Fig.5 Comparison and analysis process of runway smoothness evaluation method

3.3 应用案例

选取目前民航市场上最流行的A320 机型，输入相应的模型参数[5]。考虑到跑道的长度，设置跑道平整度评价距离的间隔为100 m；仿真速度设置为200 km/h，并考虑到A320 机型的主轮距为7.59 m，因此输入到机型的不平整激励分别为中心线以及左右两边距中心线各4 m 的纵断面曲线。在分析指标的相关性和适用性时，飞机振动响应为不同轮迹带道面激励下飞机综合的振动响应，而BBI 和IRI 指标为3 条轮迹带的平均值。

4 结果分析

4.1 飞机重心加速度响应的分布

在上述不平整激励下，收集A320 机型飞机重心加速度的时程变化样本数据，如图6所示，振动曲线表明飞机重心的动力学响应是一种随机振动状态。飞机在跑道两端的加速度值明显大于跑道中间段，这表明跑道两端的平整度状况稍差于中间段，这是因为跑道中间段飞机升力的作用使得道面所受动荷载较小，在荷载作用次数相同的情况下，跑道两端的平整度状况恶化更显著。以100 m 为评价间隔，跑道纵向共分为25 段，每段的重心加速度均方根如图7所示。整体而言，各段的重心加速度均方根都不超过2.5 m/s2，从乘客舒适性角度判断为可接受水平。图7更直观地说明平整度在跑道空间上分布的差异性，在0～100 m 和2 400～2 500 m 两端的重心加速度均方根约为中间段的2倍，乘客明显感觉到跑道的不平整差异。

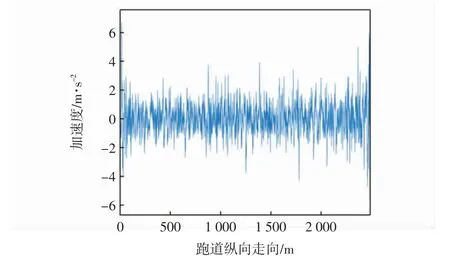
图6 飞机重心竖向加速度变化Fig.6 Vertical acceleration at aircraft gravity center

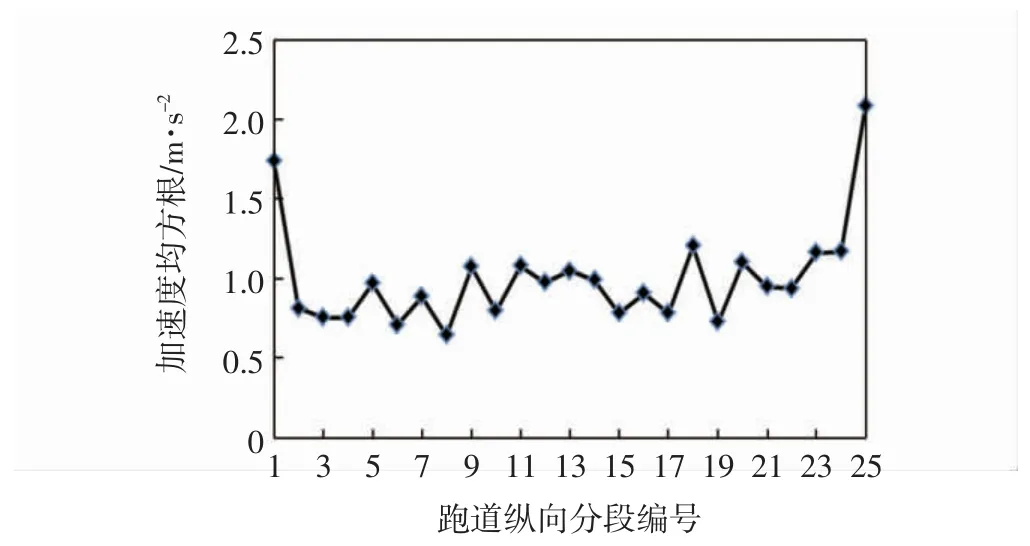
图7 飞机重心竖向加速度均方根分布Fig.7 RMS distribution of vertical acceleration at aircraft gravity center

4.2 指标相关性分析

选取图4中三维跑道的4 条测线，分别按100 m间隔计算跑道的BBI 和IRI，收集100 个两者的有效样本如图8所示。总体上，BBI 的分布归于0.2～0.9，IRI的分布不超过5.0 m/km。从两者的线性趋势上看，BBI和IRI 的相关性很低，约为0.1 左右，这是因为跑道上的不平整可看做是不同波长的波段叠加而成，IRI 的敏感波段为0～5 m 的短波段，而BBI 的敏感波段可延伸至120 m 的长波段。因此BBI 和IRI 在评价同一跑道时表现出巨大的差异。从目前规范上的评价标准分析，该4 条测线的BBI 均在1.0 以下，处于可接受区；而IRI 有95%处于“好”、2%处于“中”、3%处于“差”的评价段，两者在评价标准上也出现了差异。综上所述，IRI 和BBI 两者的相关性较差，将两者同等看待作为评价指标可能将得到不同的维修结论，因此建议以1个指标为主、另1 个指标为辅的策略进行跑道平整度评价。

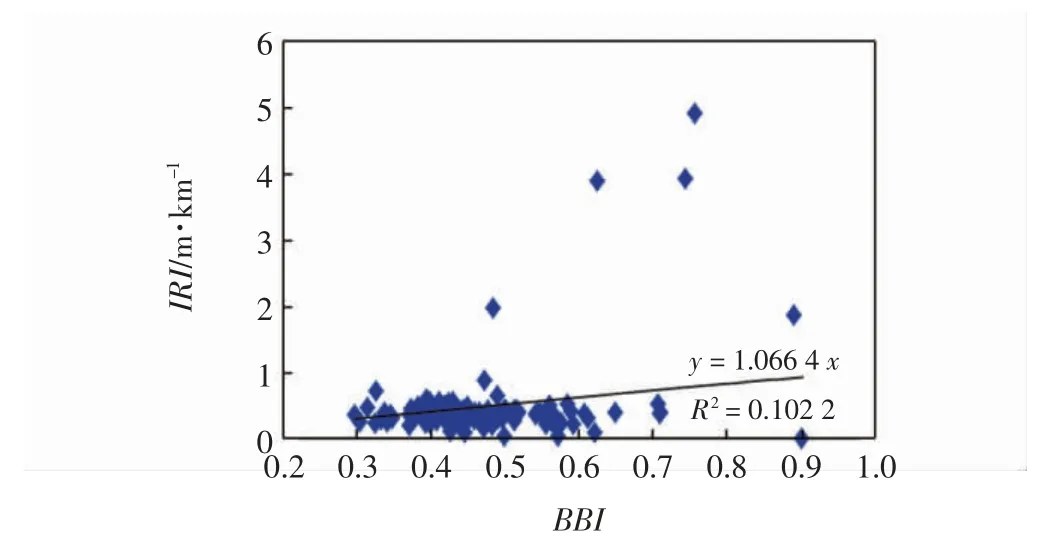
图8 BBI 和IRI 指标的相关性分析Fig.8 Correlation analysis of BBI and IRI

4.3 指标的适应性分析

按100 m 间隔收集跑道纵断面对应A320 机型重心竖向加速度均方根RMS 和BBI 及IRI 数值如图9和10 所示。从竖向整体上看，BBI 的走势与飞机振动响应更加贴合，特别在跑道的尾部，两者的走势基本一致；而IRI 则与飞机振动响应的相关性很差，在编号1～2 以及3～5 等少数段与飞机振动响应走势相似之外，其他段的走势基本无相似性。

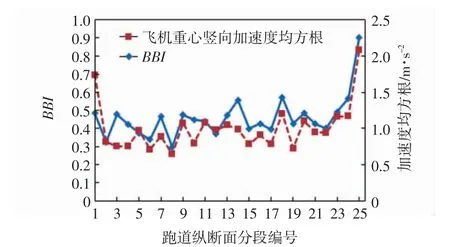
图9 BBI 和重心加速度的走势Fig.9 Trend analysis of BBI and gravity center acceleration

图10 IRI 和重心加速度的走势Fig.10 Trend analysis of IRI and gravity center acceleration

为了量化两个指标预测RMS 分布趋势的能力，将BBI、IRI 和RMS 分别归一化，归一化计算公式为

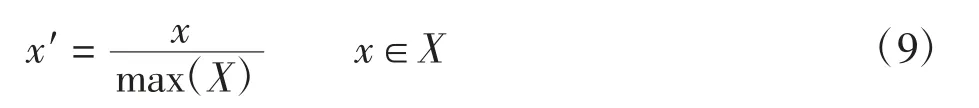
其中：x 表征各个指标在每段的值；X 表示跑道25 段该指标的集合。

3 个指标归一化后趋势分析如图11～图12 所示，定义趋势相近指数R 为

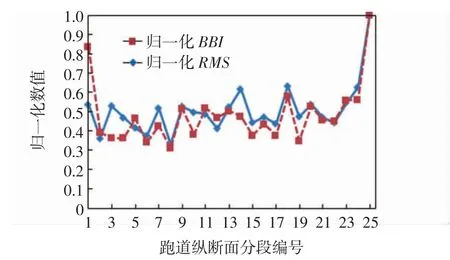
图11 归一化BBI 和重心加速度均方根的走势Fig.11 Trend analysis of BBI and gravity center acceleration after normalization

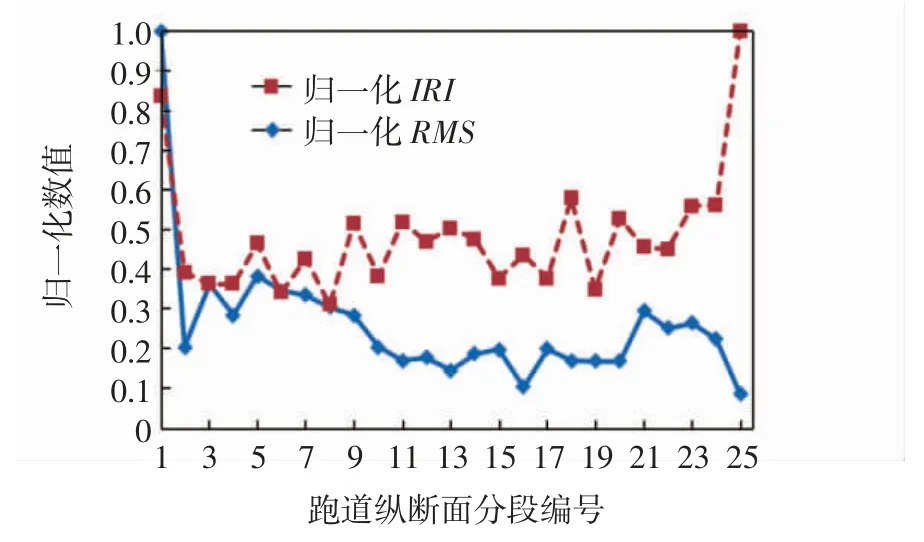
图12 归一化IRI 和重心加速度均方根的走势Fig.12 Trend analysis of IRI and gravity center acceleration after normalization

显然，当R 越小，各个指标与RMS 更贴近，预测RMS 分布趋势的能力更强。最后，计算3 个指标的趋势相近指数如表1所示。

表1 3 个指标的趋势相近指数Tab.1 Similarity index of three indicators’trends

由表1可知，BBI 的趋势相近指数更低，IRI 是BBI 的3.6 倍。这是因为BBI 指标通过飞机疲劳试验而确定的不同波长对应的振幅标准，与飞机实际滑跑的竖向加速度拟合程度更高。故建议跑道平整度评价首先考虑BBI 指标，IRI 指标可作为辅助评价指标。

5 结语

1）归纳总结了新版规范关于跑道平整度评价指标IRI 和BBI 的计算原理、评价标准，并基于Matlab 的强大的数值计算功能开发了跑道平整度评价方法对比与分析流程。

2）通过实测华东某机场跑道三维平整度数据，发现跑道两端的平整度状况比中间段更差，飞机颠簸更加剧烈。同一跑道的BBI 和IRI 基本不相关，整体的相关系数只有0.1 左右。

3）从预测飞机竖向加速度均方根分布趋势的角度，BBI 的预测能力是IRI 的3.6 倍，因此建议新版规范中应考虑将BBI 作为主要评价指标、IRI 作为辅助指标，在平整度较差的区域，可综合考虑两者做出更科学合理的养护维修决策。