A电商智能仓储中心高效均衡拣选作业优化设计
□ 王 旭,陈增坤,余 蕾
(青岛理工大学 管理工程学院,山东 青岛 266520)
1 问题的提出
1.1 问题背景
A电商智能仓储中心的基本作业包括“入库—盘点—补货—拣货—打包—出库”等,搬运作业是由AGV小车完成,其中拣货作业是一项繁重的工作,拣选作业成本约占物流中心总作业成本的60%~80%,分拣时间约占物流中心总作业时间的40%~60%,尤其在电子商务环境下,配送时限要求越来越高,拣货的效率和质量不仅影响到电商物流中心的运营成本,还影响到客户订单的满意度。因此,提高拣货作业的效率和质量,在降低电商物流中心运营成本和提高对客户的服务水平方面具有决定性作用。
1.2 问题分析
在A电商物流中心长期运营中发现,根据拣选站台的小件波次单数量来分配拣选站台、根据小件波次单时间先后确定拣选顺序是不合理的。首先,由于不同小件波次单调度的移动货架位置不同,移动货架到达拣选站台的距离不同,仅按照小件波次单数量分配会造成移动货架到拣选站台的搬运距离较长,造成不必要的搬运浪费,增加搬运成本;其次,同一拣选站台的不同小件波次单可能调度同一移动货架,仅按照小件波次单时间先后确定拣选顺序会造成同一货架在不同时段重复搬运,导致拣选站台内部作业出现忙闲不均衡现象,增加拣选时间,降低作业效率。
为解决电商物流中心拣选作业过程中出现的上述问题,就需要对小件波次单进行合理的拣选站台分配并对拣选站台内部小件波次单进行排队优化,确定合理的拣选顺序,使得移动货架到拣选站台搬运距离最短、拣选站台内部拣选作业任务均衡,从而降低搬运成本,提高拣选作业效率。
2 基于货架搬运距离最短的分配模型
2.1 小件波次单分配模型设定
在该模型中需要计算移动货架总的搬运距离,已知A电商智能仓储中心共有6个拣选站台,此外对系统做出如下假设:
①小件波次单数量已知;
②小件波次单所调度的移动货架信息已知;
③一个货架在同一个波次中只能被搬运一次;
④不存在缺货的情况;
⑤小件波次单中商品信息已知,并且商品品项在移动货架中的储位已知。
同时,在模型的建立中,设置了如下参数,并对其进行了定义,如表1所示。

表1 小件波次单分配模型所用参数符号及含义
另外,
2.2 小件波次单分配模型的建立
根据以上的模型假设及其参数设置,可以将本文研究系统的小件波次单分配问题描述为:假设一个小件波次单j分配到第β个拣选台,使得小件波次单j调度的各个移动货架到第β个拣选站台的搬运距离之和最小。因此,本文中所研究系统的小件波次单分配问题的数学模型如下:
目标函数:
约束条件:
其中为目标函数表示一个小件波次单j调度的各个货架到第β个拣选站台的搬运距离总和最短,从而确定β的数值,即确定小件波次单j分配的拣选站台序号;约束条件表示每个小件波次单只能被分配到一个拣选台,共有6个拣选台进行选择。
2.3 小件波次单分配模型的求解
将小件波次单j分别分配到第β(β=1,2,3,...,6)个拣选站台,分别测量小件波次单j调度的移动货架i(i=1,2,3,……N)到第β个拣选站台的搬运距离Siβ,计算小件波次单j调度的全部移动货架到第β个拣选站台的搬运距离之和Sjβ,依次遍历g(g≤6)个拣选站台,从而确定β的数值,使得Sjβ最小。
同理,遍历所有小件波次单,求解最短的移动货架搬运距离Sjβ,分别确定对应的j与β的数值,本文采用广度优先遍历法借助MATLAB软件编程对上述模型进行求解,从而完成所有小件波次单拣选站台的分配。
3 基于货架搬运次数最少的排队模型
3.1 小件波次单耦合因子的确定
第β个拣选站台的小件波次单总量用Qβ表示,Qβ可表示为:
其中,m表示小件波次单数量,g表示拣选台数量。
小件波次单j可表示矢量(xji,xj2,…,xjN),其中,xji(1≤i≤N)表示小件波次单j是否需要移动货架i,N为全部的移动货架数量。当需要移动货架i时,xji取值1,反之取值0,m个小件波次单可表示为m行、N列矩阵:
第β个拣选站台的小件波次单拣选顺序可表示为矢量(τβ1,τβ2,…,τβQβ),其中,τβj(1≤β≤g,1≤j≤Qβ)表示小件波次单j被分配至第β个拣选站台,且在该拣选站台中,拣选顺序为j,g个拣选站台的订单拣选顺序为:
其中,当m%g≠0且1≤β≤m%g,m%g≤k≤m时,Qβ=Qk+1,因此,g个拣选站台的小件波次单拣选顺序为Qβ×g阶矩阵,令τkQβ=0。
第β个拣选站台,拣选顺序为j和j+1的小件波次单分别为τβj、τβ(j+1),为简化符号,将上述两个小件波次单记为λ、γ,则拣选小件波次单γ和小件波次单γ所需移动货架出入列次数为:

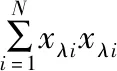
3.2 小件波次单排队优化聚类模型的建立
当同一拣选站台的小件波次单所调度的共需移动货架出入列次数最少时,移动货架的准时到达率最高,人工的空闲时间最少,从而达到拣选站台内部作业任务均衡,拣选作业效率最高,因此小件波次单排队优化的目标可由拣选站台内部作业任务均衡的目标转化为减少的移动货架出入列次数最大化,由此建立的目标规划模型如下:
目标函数:
约束条件1:
约束条件2:
约束条件3:
其中,目标函数表示为分配在拣选站台β的小件波次单j和小件波次单j+a,当按照拣选顺序k进行拣选时,小件波次单调度的移动货架出入列次数最少;
约束条件1中的ρjkβ表示小件波次单j是否在拣选站台β,以及在拣选站台β的拣选次序是否为k,当拣选次序为k时,ρjkβ取值1,反之取值0;
约束条件2表示小件波次单j所在的拣选站台β有唯一的拣选次序k;
约束条件3表示拣选站台β每次拣选作业仅分配一个小件波次单。
3.3 小件波次单排队优化模型的求解
小件波次单派对优化问题可归结为TSP问题。K-Means聚类算法在处理多簇集问题时,具有收敛速度快的特点,适用于中等规模的数据聚类处理。因此,本文采用K-Means聚类算法对小件波次单排队优化模型进行求解。
Step1:首先计算拣选站台β的j个小件波次单中,两两小件波次单之间的耦合因子,计算次数为Qc=j(j-1)/2,得到该拣选站台中每个小件波次单与其他小件波次单之间的耦合因子矩阵:
其中,Fλγ(1≤λ≤j,1≤γ≤j)为小件波次单λ与小件波次单γ的耦合因子。当λ=γ时,Fλγ=0,即每个小件波次单与其自身的耦合因子为零。
Step2:对小件波次单λ(1≤λ≤j)与其他小件波次单的耦合因子Fλγ(1≤λ≤j)进行排序:
Fλ1≥Fλ2≥Fλ3≥…Fλ(j-1)
Step3:耦合因子排序完成后,应用以下算法步骤对模型进行求解。
3.3.1 为拣选站台设置初始小件波次单
①为拣选站台β(1≤β≤g)设置标志位θβ=0,表示该拣选站台中的小件波次单数量。当时θβ=0时,拣选站台β无初始小件波次单;θβ时,拣选站台β有初始小件波次单。
②遍历拣选站台β的j个小件波次单与其他小件波次单的耦合因子,查找最大的Fλγ,小件波次单λ和小件波次单γ在拣选站台β中的拣选顺序分别为1,2,即τβ1=λ,τβ2=λ,拣选站台β的小件波次单数量顺序变为2,即θj=2。
3.3.2 确定拣选站台其余小件波次单的拣选顺序
①令λ=1。
②搜索拣选站台β中拣选顺序为θλ的小件波次单ω,遍历小件波次单k与其他小件波次单的耦合因子,查找小件波次单υ,使其满足Fωυ最大。令θ=θλ,则τβ(θ+1)=υ,θλ=θλ+1。
③判断是否已经完成所有小件波次单的排队,如果λ A电商智能仓储中心的小件拣选作业均在拣选站台完成,拣选站台按照小件波次单进行拣选作业。由于不同小件波次单调度的移动货架不同,而不同移动货架到各个拣选台的位置不同,因此将小件波次单依据移动货架搬运距离最短的原则分配拣选站台,可以有效缩短搬运距离、减少搬运时间。小件波次单完成拣选站台分配后,按照移动货架出入列次数最少的原则,对同一拣选站台的小件波次单进行排队优化,确定合理的拣选顺序,实现拣选站台内部作业任务均衡,作业效率最高。通过小件波次单的分配、排队模型,可以有效减少搬运浪费,提高拣选作业效率,最大程度降低智能仓储中心运营成本。 在A电商智能仓储中心的拣选作业中,首先采用基于移动货架搬运距离最短的原则将小件波次单分配到各个拣选站台,在此基础上,采用基于移动货架出入列次数最少的原则对分配到各个拣选站台的小件波次单进行排队,确定合理的拣选顺序。通过以上两个优化模型,可有效解决仓储中心由于移动货架搬运距离较远造成的搬运浪费、由于移动货架出入列次数较多造成的拣选站台内部作业任务不均衡,拣选作业时间较长的问题,从而最大程度提高A电商智能仓储中心拣选作业效率,降低运营成本。4 小件波次单优化模型效果分析
5 结论

