机枪胶泥缓冲器动力学仿真分析

王虹琴，苏铁熊，马富康，王东华，王 伟

（1.中国北方发动机研究所,天津300400；2.中北大学,太原030051）

0 引言

大口径狙击步枪主要依靠动能弹在1000m～1500m范围内精准打击指挥员、步兵战车、武装直升机、雷达、导弹发射装置等高价值目标。在城市作战中，远距离打击不仅可以有效消灭目标，还可以避免对平民造成伤害；在野外作战中，远距离精准打击可以减少弹药的消耗，提高作战持久性。另外，战场上的精准打击所达成的震慑效果可有效限制敌方行动，并产生极大的心战作用。但是，巨大的后坐力和发射时的声音、烟雾严重影响性能的发挥[1]。现代战争对武器作战的性能要求越来越高，以12.7mm机枪胶泥缓冲器后坐质量为研究对象，运用Adamas对后坐复进过程中后坐质量运动的位移与时间、速度与时间、后坐阻力与时间之间的关系进行仿真分析，尽可能降低后坐阻力，增大后坐行程，使机枪射击晃动减小，更加精准。

1 机枪胶泥缓冲器工作原理

机枪胶泥缓冲器由活塞、胶泥、缸盖、活塞缸、缸筒及密封装置所构成[2]。将预压力设置为2100N。以后坐部分为研究对象，当后坐部分质量所受到的外力小于2100N时，后坐部分静止不动；当后坐部分受到的外力大于2100N时，活塞压缩胶泥，因此后坐部分将整体向后运动。在后坐过程中，速度阻尼力减小，弹性力增大；在达到缸底时开始复进，速度阻尼力增大，弹性力减小。整个后坐和复进的过程就是一个消耗能量的过程[3]，如图1所示。

图1 胶泥缓冲器二维结构图Fig.1 2D structure diagram of Silicon-based elastomer damper

2 胶泥力学特性

设计一种胶泥缓冲器来代替传统的弹簧缓冲器，传统的弹簧缓冲器冲击大、反弹大，且经长期使用容易变形，而胶泥缓冲器可以克服这些缺点。将胶泥材料引入缓冲、减振设备的目的主要在于胶泥既有固体的弹性，又有液体的流动性，这使得胶泥可以在同一运动中既利用弹性储蓄了复位所需的能量，又利用流动阻尼性起到了耗能的作用。在同一次运动中，同一种材料可以完成两种不同的任务，这可以在大大简化缓冲器结构的同时改善缓冲器的密封特性[4]。但是，胶泥的配方不同，材料的力学特性也就不同。因此，研究胶泥材料的力学特性也是解决缓冲器性能的关键。胶泥的Maxwell模型如图2所示，其可被简化为一个弹簧与阻尼的串联结构。

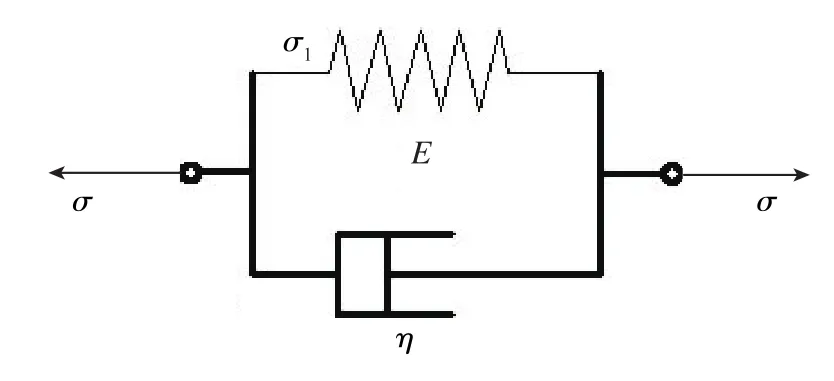
图2 胶泥的Maxwell模型Fig.2 Maxwell model of Silicon-based elastomer damper

2.1 预压力F0

缓冲器预压力产生的原理是将大于缓冲器容量的胶泥压入缓冲器并产生预压体积变形，因此，缓冲器预压力的计算公式如下

其中，V0为胶泥预压体积。

胶泥预压体积、胶泥体积及缓冲器容量满足如下代数关系

式中，Ve为缓冲器容量。

预压力不可过大，如果预压力过大，则需要很大的后坐力才能使缓冲器开始工作。这样就会带来撞击，增加枪体的不稳定性，影响射击精度。预压力也不可过小，如果预压力过小，则达不到应有的缓冲效果。一般而言，预压力用于抵消摩擦力和重力的分力。在设计过程中，缓冲器容量通常是已知量，其他两个是未知量，可以根据已知关系求出。

2.2 胶泥体积压缩产生的弹性力fs

由胶泥的特性可知，在缓冲器工作过程中，胶泥体积压缩会产生弹性力。其大小也是衡量胶泥性能的指标之一，它与胶泥本身的储能模量有关。

在计算缓冲器弹性力时，由于需要将胶泥与缓冲器结合起来考虑，在使用储能模量时非常不方便。因此，可借鉴流体力学中描述可压缩流体的压缩性的体积模量概念来计算。

体积模量的定义为：当流体的温度保持不变时，由单位体积变化引起的压力变化可被称为体积模量，用E表示

由体积模量的定义可知

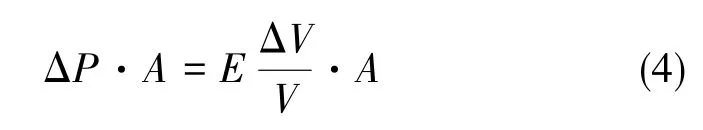
则有

式中，A为缸桶内径横截面，V为胶泥体积，Ah为活塞截面，x为活塞行程。

2.3 由胶泥粘滞阻尼产生的阻尼力fv

为了建立阻尼力和缓冲器实际物理参数的关系，作如下假设：

1）阻尼器活塞以恒速v运动；

2）阻尼通道的间隙尺寸远小于缓冲器缸体的内径尺寸；

3）胶泥材料为各向同性流体；

4）胶泥流动时在管壁处无滑移。

根据假设2，可以将阻尼通道的同心环型间隙在平面展开为平行板间的流动问题，如图3所示。

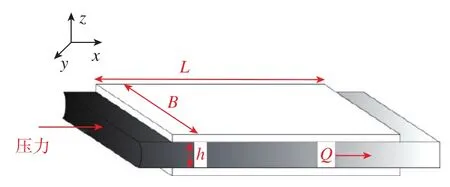
图3 胶泥平行板流动Fig.3 Parallel flow of Silicon-based elastomer damper

则平板长L为胶泥的等效工作长度，平板的等效宽度为

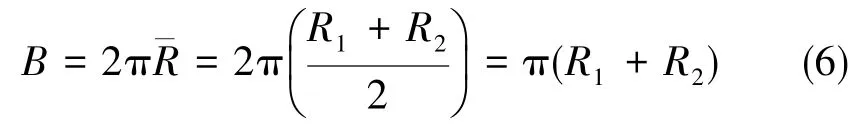
其中，R1和R2分别为缸体内径和活塞外径，平行板间的板间距为h，且h=R1-R2，为同心环的间隙高度。

为了分析胶泥对活塞的阻尼力，从缓冲器缸体与活塞之间的流体中取出一个微小长方体单元。一个面取至缸体内表面，另一个面取至活塞的外表面。由于两个面均较小，可以将其近似看作平行面，并且两者之间的距离为h，如图4所示。该微单元体的流动情况可被假设为两平行板之间的流动，其中一板静止不动，另一板突然以速度U运动。根据假设4，可知胶泥在上板、下板处的流速分别为：vs=0、vx=-U。

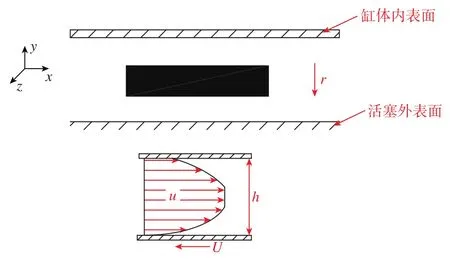
图4 胶泥流动速度分布Fig.4 Flow velocity distribution of Silicon-based elastomer damper

由以上分析可知，胶泥速度与缓冲器速度并不一致，但是存在一定关系。为了研究胶泥在缓冲器中产生的阻尼力的大小，关键问题是解决胶泥流速与缓冲器活塞杆运动速度的关系。对于所考虑的问题，将胶泥流度写成如下表达式

式中，u为x方向的速度，为x方向的单位矢量，则动量方程为

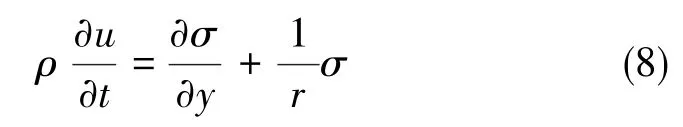
式中，ρ为胶泥密度，τ为应力。

胶泥的本构方程为

连列式（7）和式（8），消去应力张量σ，得到关于速度的方程

式中，μ为胶泥动力黏度。

根据假设4，可知边界条件为

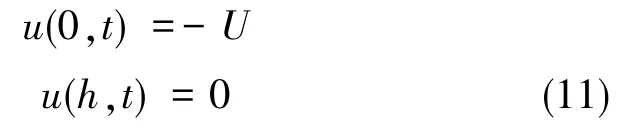
由此可解得流体速度的表达式，由于方程中带有分数微分，求解过程繁琐，而经典的Maxwell粘弹性模型推导的结果是二阶微分，因此考虑将分数微分化简为负数二阶微分求解，在结果中增加一个速度相关指数n，用来符合公式误差和实际误差，带入边界条件求得

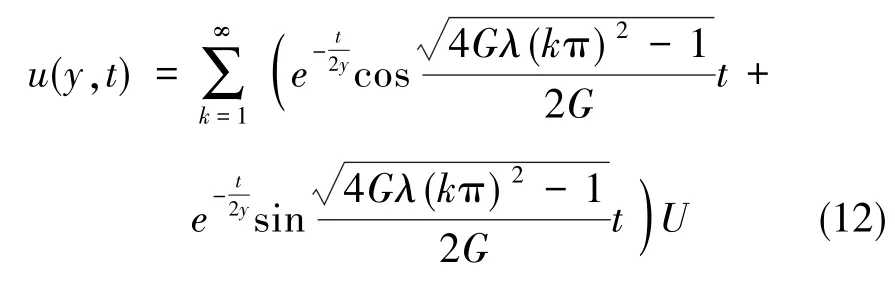
式中，λ=μ/G，为胶泥松弛时间，将其代入式（12），则有

由于冲击总是于瞬间完成，所以最重要的是由活塞和缸体之间的相对运动引起的流体流动的瞬时速度。

为了简化计算，将流体速度带入经典的Maxwell模型，可得流体阻尼内部剪切力的近似计算公式

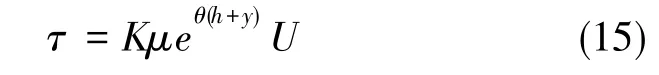
式中，K为切应力系数，取决于冲击实验环境；θ为补偿系数。

为了提高缓冲器的回弹速度，拟定取消环形间隙，即在h=0、y=0位置（活塞边缘及取消活塞与缸筒间的环形间隙），流体的切应力计算公式为

因此，胶泥流体产生的阻尼力计算公式为

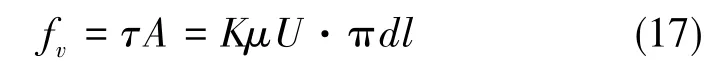
式中，d为活塞的直径，l为活塞的长度。

但是，根据大量实验及参考文献中的叙述，阻尼力公式并不一定与活塞速度呈线性关系。因此在该公式的基础上，做出一定的改进

改进公式在原推导理论公式的基础上，增加了一项速度相关指数n，作为速度的指数。一般n取0.4～0.45，使阻尼力公式更加真实。

因此，缓冲器后坐的阻抗力计算公式如下

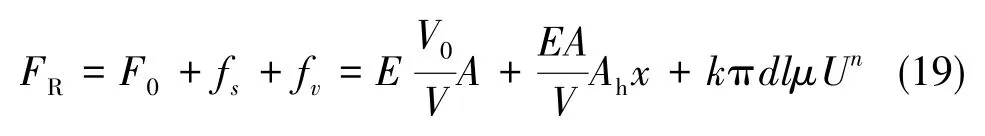
式（19）也称为后坐阻力方程。

3 缓冲器运动学模型建立

射击时，在机枪膛底合力的作用下，后坐质量发生运动（枪身、缓冲器杆等可被称为后坐质量，主要是枪身质量，缓冲器杆质量可以忽略不计）[5]。图5为机枪模型，以后坐部分为研究对象进行受力分析。对图5的机枪模型进行简化，可得缓冲器运动学简化模型，如图6所示。Fpt为膛底合力，mh为后坐部分的质量，FR为后坐阻力。

图5 机枪模型Fig.5 Model of machine-gun

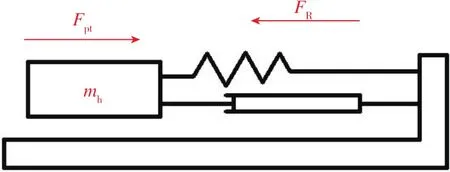
图6 缓冲器运动学简化模型Fig.6 Simplified kinematics model of buffer

射击时，后坐部分由主动力、阻力、约束反力共同控制[6]。将运动方程进行简化，做出基本假设如下[7]：

1）后坐部分和除此之外的枪架部分均为刚体，且架体不动；

2）射击时所有力均在射击面上作用，假设作用力平行于地面；

3）忽略弹丸作用于膛线导转侧而产生的力矩Mx，该力矩产生的影响作用小[8]。

在此假设前提下，对后坐部分的运动进行刚体动力学分析，以枪膛轴线为x轴[9]，由牛顿第二定律可得

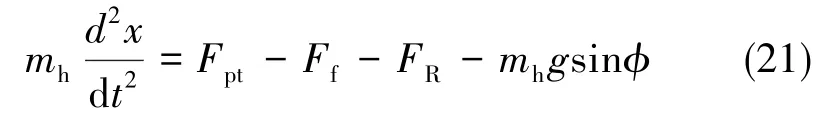
其中，Fpt为膛底合力，Ff为摩擦力，FR为后坐阻力，mhgsinφ为重力的分力，φ为射角。式（21）即为后坐部分进行后坐运动时的微分方程，其被称为制退后坐运动方程，也被简称为制退方程。

为了计算方便，假设φ为0，将式（21）表示为

式（22）表示膛底合力Fpt是机枪射击时后坐质量产生后坐运动的动力，而后坐阻力FR是与膛合力方向相反的，由速度阻尼力、弹性力与预压力组成的一个消耗能量的合力[10]。在射击过程中，这对矛盾力的存在影响着后坐部分的运动特性。在后坐质量运动过程中，膛底合力Fpt已经通过上述计算得到，而后坐阻力FR与胶泥的特性参数及缓冲器的结构参数息息相关[11]。

4 后坐过程动力学仿真分析

如表1所示，依据已知的内弹道参数，运用内弹道计算公式结合四阶Runge-kutta的方法在Matlab中进行仿真计算，得到如图7所示的膛底合力与时间的关系曲线。膛底合力为胶泥缓冲器的制退后坐运动提供了动力，而胶泥缓冲器后坐的意义在于消耗膛底合力在短时间内做功而产生的能量。

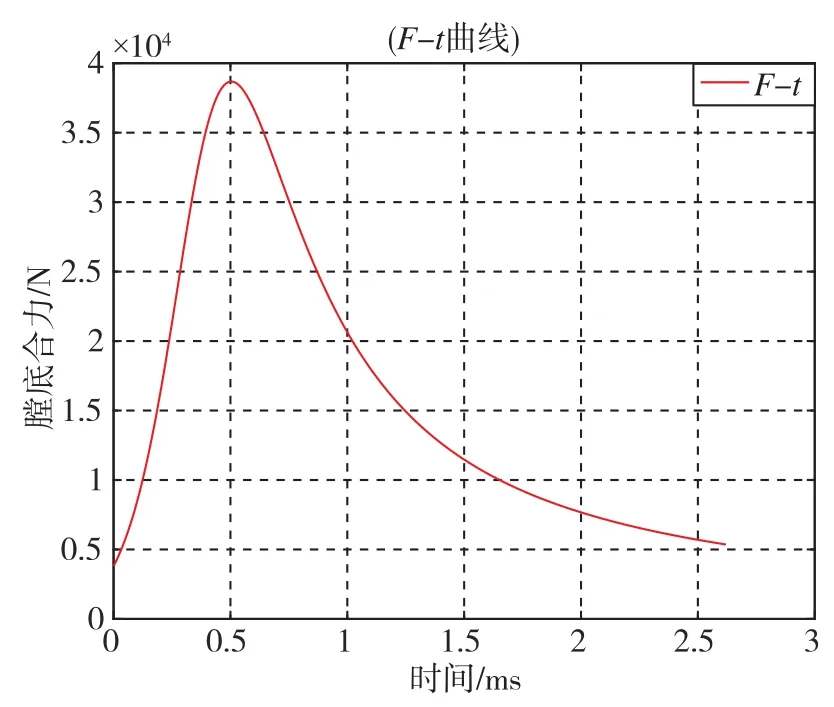
图7 膛底合力与时间关系图Fig.7 Relationship between bore force and time

从能量消耗的角度来说，胶泥缓冲器的作用就是后坐质量通过后坐制退运动消耗膛底合力在短时间内产生的能量。

设定边界条件为：在t=0、v=0时，x=0，则有

由式（23）、 式（24）可以看出，后坐运动可以看成两个力（Fpt和FR）共同作用的结果。以上两式中右边第一项可以看成在膛底合力Fpt作用下的运动，其被称为自由后坐运动[12]，简称自由后坐（缓冲器杆与枪身之间存在小间隙，在枪身没有和缓冲器杆接触之前枪身的运动是自由后坐）[13]。第二项是后坐阻力作用的运动，其被称为制退后坐运动，也被称为制退后坐[14]。

自由后坐的速度为W，位移为L，则自由后坐的运动方程为

设定初始条件：在t=0时，L=0，W=0，对自由后坐运动方程进行积分

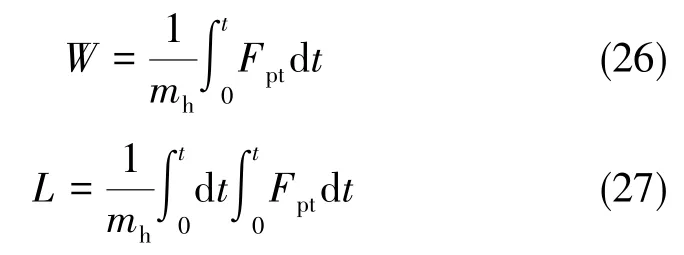
自由后坐的特点是当火药气体后效期结束后，Fpt=0，之后自由后坐运动为匀速直线运动。

将式（23）～式（26）联立，有

以上两式被称为转换方程。式（28）表示在已知膛底合力与时间的关系的基础上，易得到后坐质量在制退后坐过程中的位移、速度、后坐阻力与时间之间的关系。

从理论上分析了后坐质量在后坐过程中的位移、速度、后坐阻力与时间之间的关系，又运用ADAMS软件进行了动力学仿真计算[15]：

1）根据胶泥缓冲器二维图纸，建立了胶泥缓冲器三维模型；

2）导入x-t格式；

3）设定胶泥的弹性系数、阻尼系数及缓冲器各零件的质量参数；

4）设置约束和施加载荷（这里的载荷是指导入计算所得的膛底合力）；

5）测量后坐质量在制退后坐过程中的位移、速度、后坐阻力与时间之间的关系。

测量后坐质量在制退后坐过程中的位移、后坐阻力、速度与时间之间的关系，得到的结果如图8～图10所示。

图8为后坐部分在后坐复进过程中的位移与时间的关系：从0s开始，胶泥缓冲器后坐部分进行后坐运动；在0.018s时，后坐部分碰撞到底部，后坐位移达到最大，为7.5mm；后坐部分开始进行复进运动，到0.032s碰到缸盖时速度为0，后坐复进运动结束。相比传统的弹簧缓冲为4.8mm的行程而言，增大了将近1.5倍。

图9为后坐部分在后坐复进过程中的后坐阻力与时间的关系。胶泥缓冲器后坐阻力受弹性力、预压力、速度阻尼力三个力的控制，其中预压力始终存在。在0s时，后坐阻力的大小仅为预压力的大小，其他两项都是0。从0s开始，速度阻尼力不断增大，弹性力也增大，后坐阻力因此不断增大，达到负方向最大速度之后，速度阻尼力开始减小，弹性力反方向继续增大，但后坐阻力总的趋势依然是继续增大。在0.018s时，胶泥缓冲器后坐部分到达缸底，速度阻尼力为0，总的后坐阻力达到最大，为5700N。此后，速度阻尼力正方向增大，弹性力减小，总的后坐阻力持续减小。在触碰到缸底时，速度阻尼力瞬间为0，后坐部分复进到原来的初始位置，弹性力为0，后坐阻力的大小仅为预压力的大小，后坐阻力瞬间恢复到2100N。

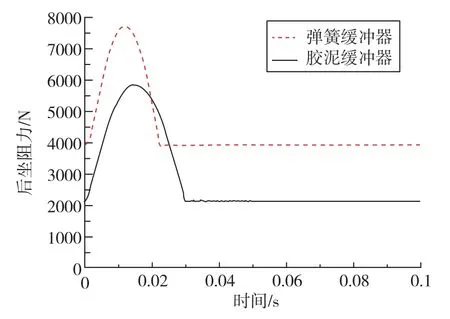
图9 后坐复进过程中的后坐阻力与时间关系Fig.9 Relationship between recoil resistance and time

图10为后坐部分在后坐复进过程中的速度与时间的关系。从0s开始，胶泥后坐部分从0开始在负方向增大速度；在0.004s时，后坐部分达到795mm/s的最大速度，然后在负方向上不断减小；在0.018s时，速度减小到0，之后反方向速度增大；在0.032s时，速度达到820mm/s；在碰到缸盖时，速度迅速下降为0。

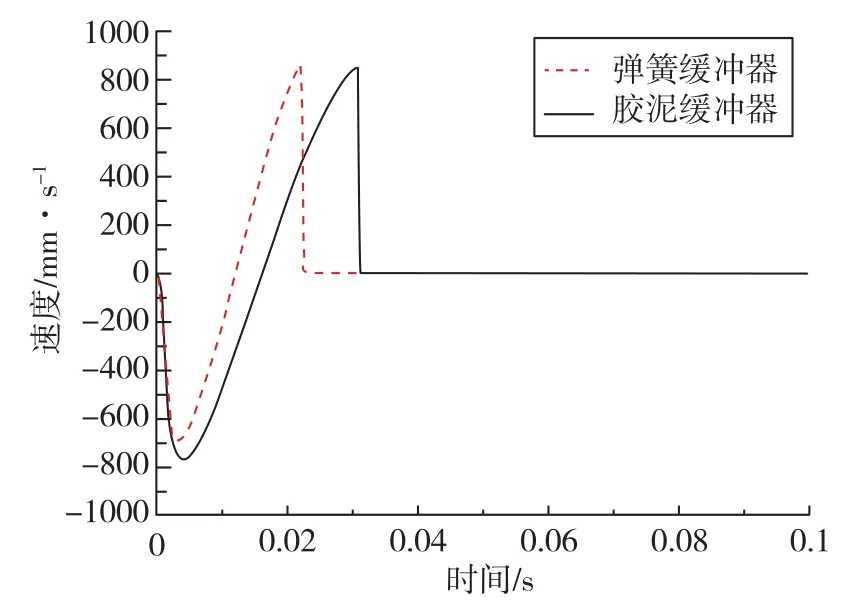
图10 后坐复进过程中的速度与时间关系Fig.10 Relationship between velocity and time

5 机枪稳定性验证

枪口动态响应即枪口跳动的角度与竖直位移，是考量机枪射击稳定性和精准度的指标。子弹击发后，火药气体作用于膛底（膛底合力即初始后坐力），形成翻转力矩，引起枪口上跳，枪口位移逐渐增大；当子弹运动经过胶泥缓冲装置后，缓冲装置吸收能量，提供阻抗力，后坐力减小，翻转力矩减小，枪口跳动的竖直位移和角度也随之减小。

弹丸出膛口时刻为子弹击发之时的开始，再经过短暂的内弹道时间。建立ADAMS胶泥缓冲器模型及传统的弹簧缓冲器模型，分别对活塞杆施加一组膛底合力的样条力，在枪口机建立一个Mark点，用来检验竖直方向的枪口位移，位移越小，则机枪稳定性越高。

将胶泥缓冲装置应用于机枪系统，以ADAMS软件仿真系统为平台进行动力学仿真，如图11所示。通过对比可以看出，在机枪结构改进后，使用胶泥缓冲器的机枪枪口的最大波动为12.5mm，而使用弹簧缓冲器的机枪枪口的波动为14mm。枪口跳动的最大位移下降了12%，胶泥缓冲器在提高射击精度方面作用明显。

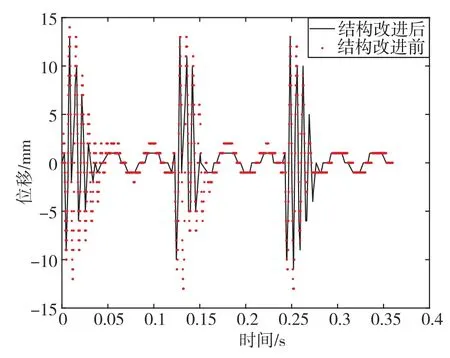
图11 结构改进前后高低方向的位移曲线对比Fig.11 Comparison of high and low directional displacement curves before and after structural improvement

6 结论

根据上述分析可知，在满足1min 600发的射击频率下，新型胶泥缓冲器与弹簧缓冲器相比，增长了后坐行程，在机枪后坐复进过程中消耗了能量，使得机枪射击更加平稳，提高了机枪射击的精度，在实际应用中是非常有意义的。