一种基于光纤捷联惯性系统大样本统计的参数有效期评估方法

何小飞，岳栋栋，梁加红，吴立秋

（1.国防科技大学系统工程学院,长沙410073；2.北京航天时代光电科技有限公司,北京100094）

0 引言

光纤陀螺惯性测量装置（以下简称 “光纤惯组”）是由光纤陀螺、加速度计及有关电路构成的子系统，可测量运载体相对于惯性空间的线运动和角运动。光纤惯组的标定是在准确已知输入量的条件下测试光纤惯组的输出并通过相关的计算确定模型中各个系数的具体数值的过程，模型中各个系数的具体数值即为标定参数[1]。由于光纤惯组零部件的材质为多种金属、非金属，在加工等多种因素的影响下（如金属材料的应力释放，非金属材料的蠕变、老化，永磁材料的自然退磁等），随着贮存时间的延长，光纤惯组的部分标定参数会产生漂移。当漂移量超出一定范围后，光纤惯组将难以满足性能指标要求。为保证测量精度，应对光纤惯组重新进行标定。

目前，国内外相关研究主要集中于外场自标定、多位置标定等系统级标定[2-5]，利用Bayes方法、随机加权法、最大熵方法等对小样本惯组的历次测试数据进行分析[6-7]，对部分参数误差的产生机理进行研究[8-9]。文献[10]对参数的稳定性进行了分析，但只积累了1套产品在4个月内的数据。国内外研究样本少，数据积累时间短，误差机理分析多针对于短时间内的变化特性。

标定参数有效期是武器系统在使用过程中的一项重要指标，它决定了定期标定的周期。从抽测光纤惯组测量的情况来看，该指标有一定裕量。传统抽测方法样本较少、覆盖性不足，大批量光纤惯组在交付部队使用后不具备在有效期内进行多次测试的条件，在批量光纤惯组标定参数超出有效期后，需将其从武器上拆下并重新进行标定。以此为契机，可积累大批量光纤惯组单次的测试数据。本文对标定参数误差的产生机理进行了分析，统计了批量光纤惯组参数在有效期满后进行单次测试的标定参数误差，探索出了一种评估标定参数有效期的新方法。该方法样本量大，无需在有效期内进行多次测试，不影响武器系统的正常服役。

1 试验方案及评估方法

目前，传统的参数有效期测试方法为抽测个别产品，即在有效期内均匀分配测试时间，进行多次测试（测试次数不少于6次），并根据测试结果考核参数有效期是否满足要求[11]。本文提出的试验方案为对参数有效期满的多套产品进行单次测试，根据测试结果来考核标定参数是否满足了性能指标要求，即参数有效期是否满足要求。

根据传统测试方法，光纤惯组的标定参数可被划分为两类：1）根据单套光纤惯组的单次试验即可得到1σ统计值，包括光纤陀螺一次通电稳定性、光纤陀螺随机游走、加速度计一次通电稳定性；2）根据单套光纤惯组的多次试验才可得到1σ统计值，包括光纤陀螺常值漂移、加速度计零位误差、加速度计在±g输入条件下的标度因数误差、光纤陀螺标度因数误差。而本文方法对第一类标定参数进行评估，可统计多套光纤惯组的单次试验标定参数的最大值，以评估最大值是否满足性能指标要求；对第二类标定参数进行评估，可统计出多套光纤惯组的单次试验结果，利用正态分布及卡方检验对其进行统计学分析，以评估其是否满足性能指标要求。

（1）正态分布统计方法

对样本进行归一化处理，构建服从正态分布的新样本，以统计指标的合格概率。以光纤陀螺常值漂移为例，根据光纤惯组在出厂时6次位置的试验结果，可以求出光纤陀螺常值漂移的均值μ及标准差σ。在长期搁置后，光纤惯组标定参数的短期稳定性与出厂时几乎无差别，可以用σ值来表示。根据返厂后1次位置试验的数据可得光纤陀螺常值漂移B，可以按式（1）统计光纤陀螺常值漂移与出厂标定值之间的误差ΔB。

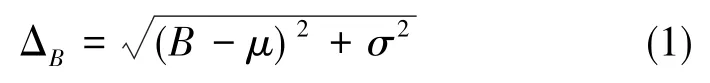
从物理意义上讲，光纤陀螺的常值漂移有正负之分，式（1）求出的只是误差的绝对值。返厂测试值减出厂测试均值的符号，即为光纤陀螺常值漂移的符号。

当测试样本量较大（一般为大于30）时，样本的分布趋于正态分布。ΔB服从正态分布，可以分别拟合出正态分布的均值m、标准差μ，并统计出正态分布满足≤1σ的概率。标定参数有68.27%以上的概率≤1σ指标，有99.73%以上的概率≤3σ指标，即认为满足要求。

（2）卡方检验方法

对标定参数长期的变化量进行卡方检验，检验问题分两类：一类为指标合格，即H0：σ≤σ0；另一类为指标超差，即H′0：σ≥σ0。n个样本符合自由度为n-1的χ2分布。考虑到样本的实际意义，公式中的S2为样本均值与标准差的平方和，计算出的样本χ2如下

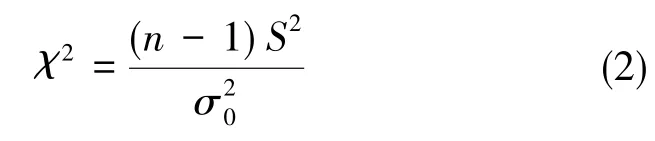
取工程中常用的检验水平α=0.05，查表可得及。如果，则接受H0：σ≤σ0；如果-0.025），则接受H′0：σ≥σ0。

此处需要说明的是，有时检验结果为接受H0且接受H′0，从常理看存在矛盾，其实这反映了统计推断的一种特点，它并不是 “非此即彼”的逻辑。原假设的选择具有倾向性，如果参数长期稳定性一贯表现较好，则检验可放宽，可选H0为原假设，要有很确定的证据才可否定H0；如果参数长期稳定性并不好，则可选较为严格的H′0为原假设，要有很确定的证据才可否定H′0。可认为两个原假设没有较明确的证据证明指标超差，也没有较明确的证据证明指标满足要求[12]。

75套光纤惯组包含了225只光纤陀螺和225只石英加速度计，统计出的光纤陀螺常值漂移和标度因数误差、加速度计零位误差和标度因数误差的柱状图分别如图4～图7所示。

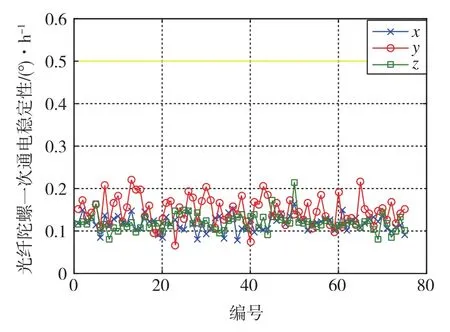
图1 光纤陀螺一次通电稳定性Fig.1 Power stability of FOG at a time

2 试验数据统计及分析

某型光纤惯组的性能指标要求如表1所示。该型光纤惯组75套产品在标定长时间后进行了1次位置试验和速率试验，计算75套光纤惯组标定参数单次的测试结果，并按上一章节的方法对标定参数进行了分类和评估。

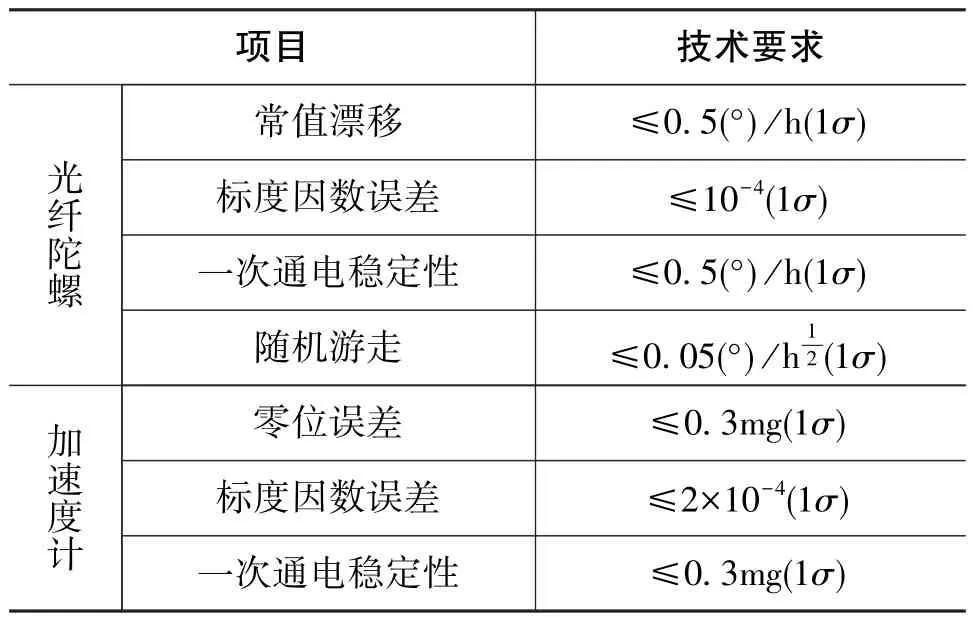
表1 性能指标要求Table 1 Performance requirements

75套光纤惯组的光纤陀螺一次通电稳定性、光纤陀螺随机游走、加速度计一次通电稳定性分别如图1～图3所示，最大值分别为0.2206（°）/h、0.0098（°）/h1/2、 0.0675mg，均100%地满足了任务书的要求。

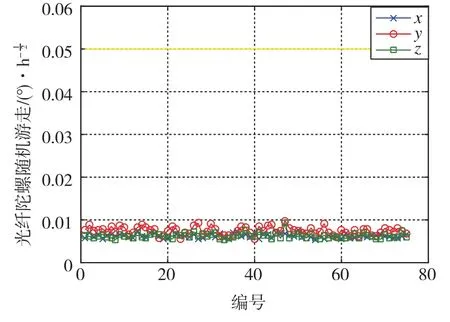
图2 光纤陀螺随机游走Fig.2 Random walk of FOG

图3 加速度计一次通电稳定性Fig.3 Power stability of accelerometer at a time

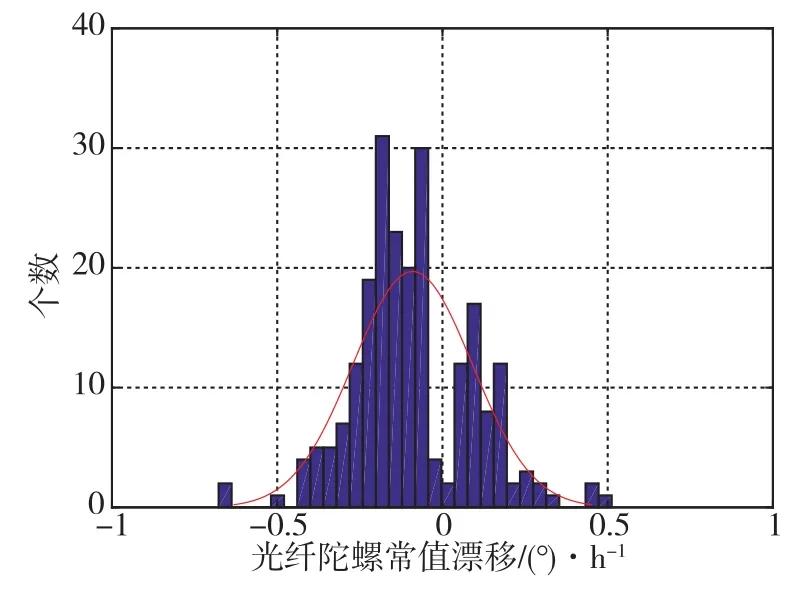
图4 光纤陀螺常值漂移Fig.4 Constant drift of FOG

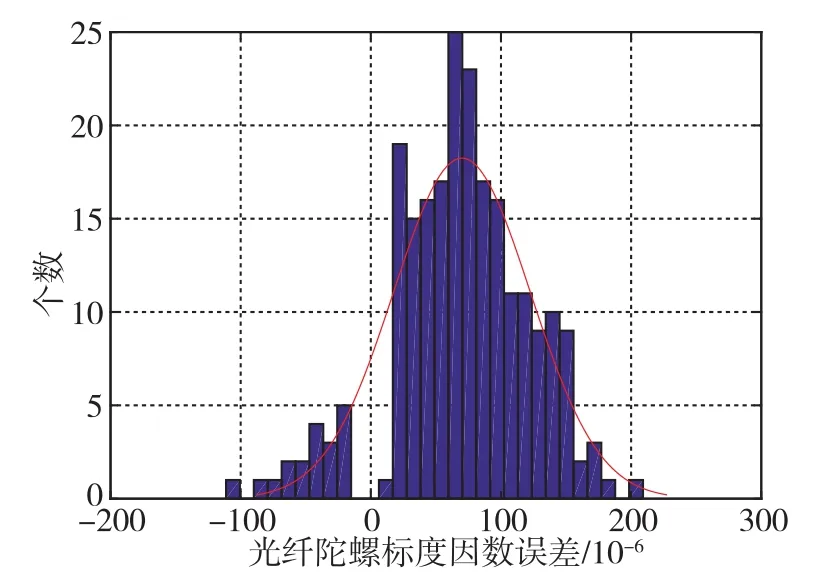
图5 光纤陀螺标度因数误差Fig.5 Error of FOG scale factor

图6 加速度计零位误差Fig.6 Error of accelerometer zero bias

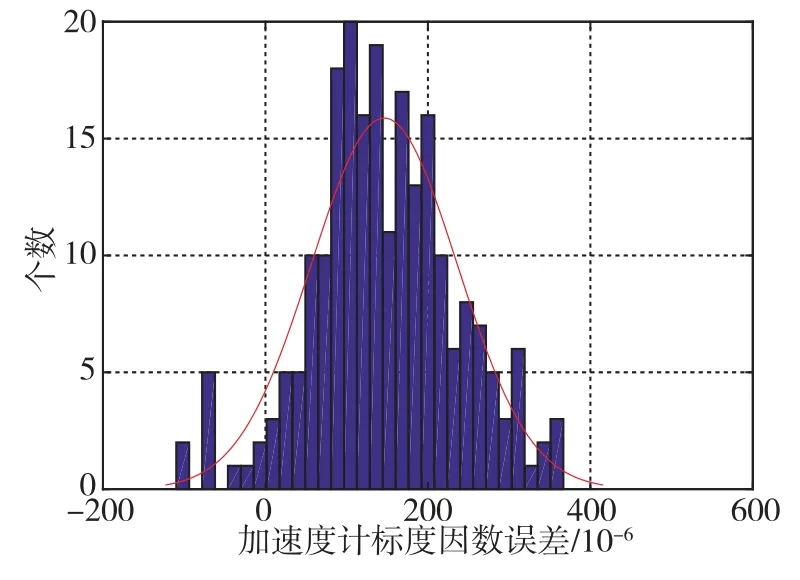
图7 加速度计标度因数误差Fig.7 Error of accelerometer scale factor

用正态分布分别对这4项标定参数进行拟合，其均值、标准差及概率统计结果如表2所示[13]，这4项标定参数均满足指标要求。在标定长时间后，光纤陀螺标度因数误差和加速度计标度因数误差不再呈零均值的正态分布，光纤陀螺常值漂移和加速度计零位误差拟合正态分布的均值仍在0附近，但加速度计零位误差正态分布的标准差较大。由此可见，光纤陀螺标度因数误差、加速度计标度因数误差、加速度计零位误差均随时间产生了较大漂移。

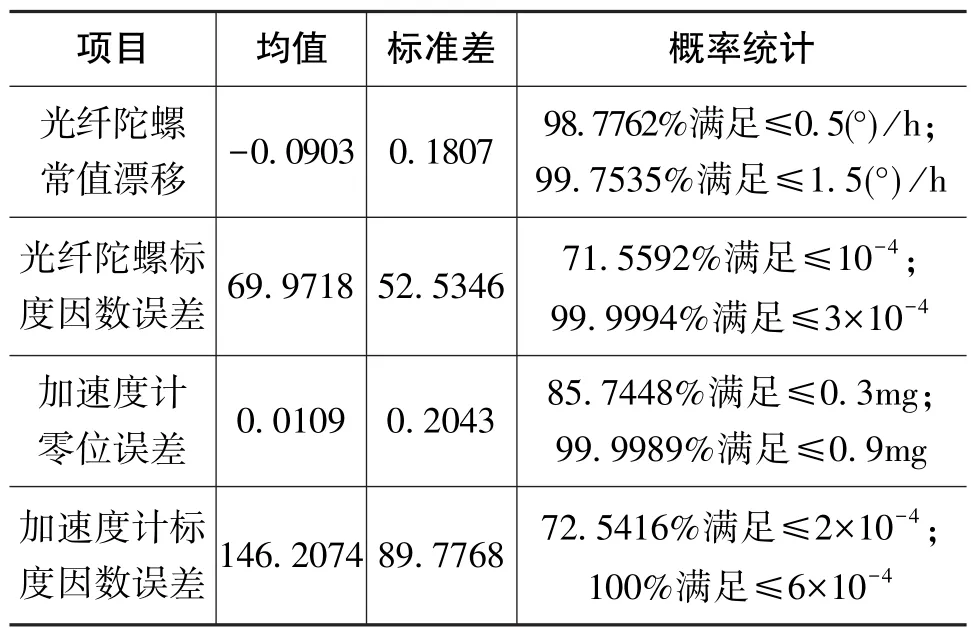
表2 225只惯性仪表正态分布拟合结果Table 2 Normal distribution fitting results of 225 inertial instruments

根据225只光纤陀螺和225只石英加速度计的测试结果，统计出光纤陀螺常值漂移和标度因数误差、加速度计零位误差和标度因数误差并进行卡方检验，查表可得。检验结果如表3所示[14]，可见4项标定参数均满足指标要求。

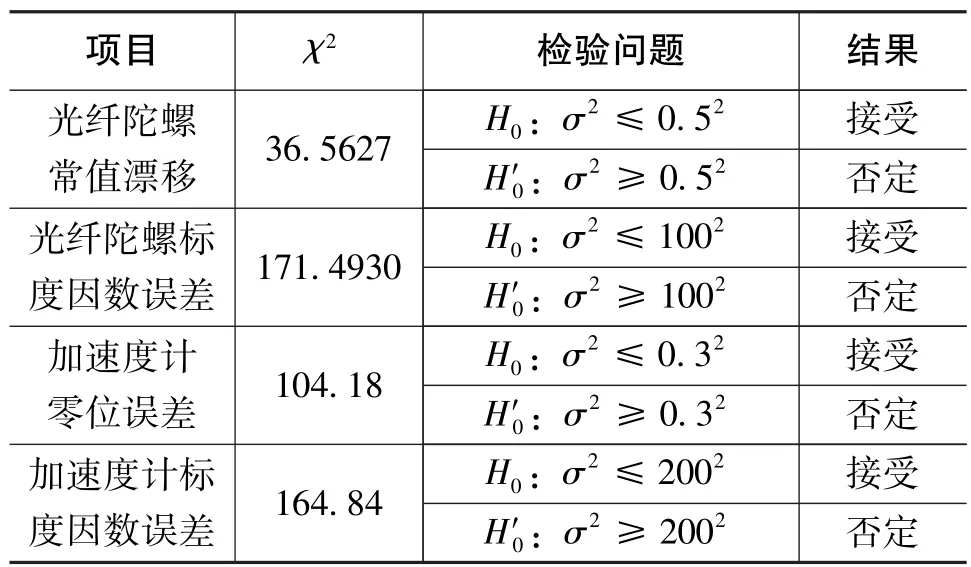
表3 4项标定参数的检验结果Table 3 Test results of 4 calibration parameters

3 标定参数误差机理分析

3.1 闭环光纤陀螺标度因数误差机理

闭环光纤陀螺（简称 “光纤陀螺”）的工作原理要求反馈相位与输入角速率的Sagnac相移的差趋近于0，即ΦFB=-ΦS。ΦFB由输出数字量通过D/A转换器、放大器和Y波导产生，ΦS可由式（3）得出

因此，可推算出光纤陀螺的标度因数[1]

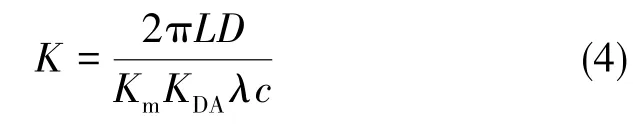
式（4）中，L为光纤环圈长度，D为光纤环圈平均直径，λ为光源平均波长，c为真空中的光速，Km为Y波导的调制系数，KDA为D/A转换器及其放大器的增益。

下面逐一分析影响光纤陀螺标度因数的因素：

1）光纤环的等效面积：光纤环采用保偏光纤并按照四极对称的方式进行绕制，在绕制过程中需要引入一定的张力，因此光纤环与骨架之间存在一定的应力分布。在经历环境变化时，骨架与光纤之间的应力发生变化，导致光纤环的有效面积的变化，从而引起标度因数的变化。但随着光纤环自身应力的逐步释放，标度因数变化幅度变小并趋于稳定。另外，光纤（主要成分为石英）自身的线膨胀使线圈等效面积产生了一个约为1×10-6/℃的典型变化，而对于中低精度光纤陀螺，这一变化可以忽略不计。

2）光源的平均波长：光纤陀螺采用超辐射发光二极管，平均波长的变化会对陀螺标度因数产生影响。目前，在产品上采用了恒流源驱动和桥式温控电路方案，对SLD光源管芯进行温度控制并对注入电流进行稳定控制，从而可以持续地将由波长漂移引发的标度因数误差控制在1×10-4的范围内。

3）Y波导的调制系数、D/A转换器及其放大器的增益：在闭环光纤陀螺方案中，Y波导、运放和D/A构成了闭环反馈通道，任一参数的变化都将使反馈增益产生误差，进而导致陀螺标度因数发生变化。陀螺采用基于四态波的反馈控制，解调复位波形在复位瞬间和复位前一个周期的探测器输出误差值，再将该值作为2π复位误差进行积分，并控制主回路D/A转换器的参考电压及控制运放的增益，可实现对闭环反馈增益误差的控制，进而确保标度因数的稳定性。

综上可见，光纤环等效面积随着使用过程中光纤环上的应力释放会出现缓慢漂移，导致光纤陀螺标度因数随时间而缓慢变化。

3.2 石英加速度计标度因数和零偏误差机理

石英挠性加速度计（简称 “加速度计”）的主要工作原理为利用摆片的惯性获得与加速度输入成比例的电流，通过对电流进行采样获得输入加速度信息。可推导出加速度计的电流输出方程，在静态时的表达式为

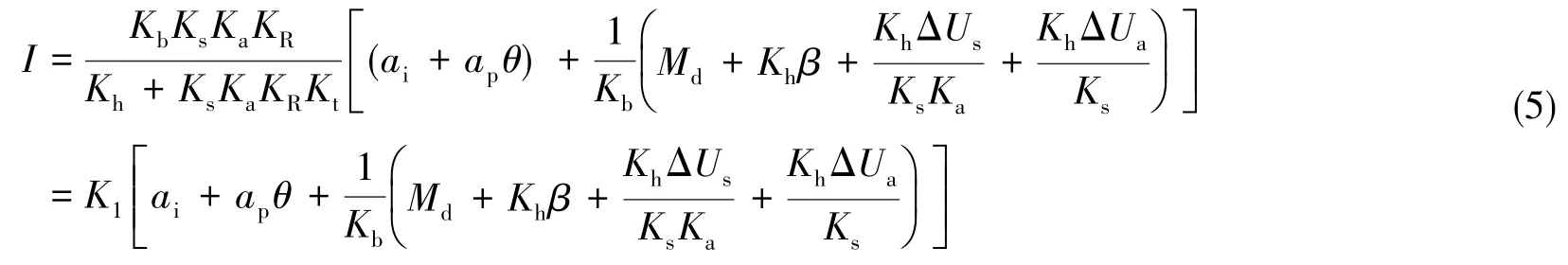
式（5）中，Kb为摆性，Md为干扰力矩，Kh为挠性摆组合刚度，Ks为信号传感器增益，Ka为伺服放大器增益，KR为负载系数，Kt为力矩器标度因数，ΔUs为伺服放大器输入干扰电压，ΔUa为伺服放大器零位输出漂移，θ为摆组件的工作角度，ap为沿摆轴方向的加速度，ai为沿输入轴方向的加速度，β为弹性恢复角（信号传感器电零位与摆组件机械零位之间的夹角）。当仪表闭环工作时，电磁反馈力矩较强，并将摆组件拉到接近信号传感器的电零位，此时在摆组件上将出现弹性恢复力矩Khβ。

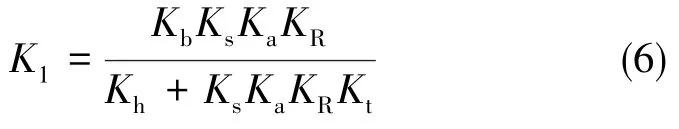
K1为加速度计的标度因数。通常有Kh＜＜KsKaKRKt，K1可近似表示为

可以看出，影响标度因数K1的因素主要包括摆性Kb和力矩器标度因数Kt。

将式（5）除以K1，即可得到加速度计的指示值

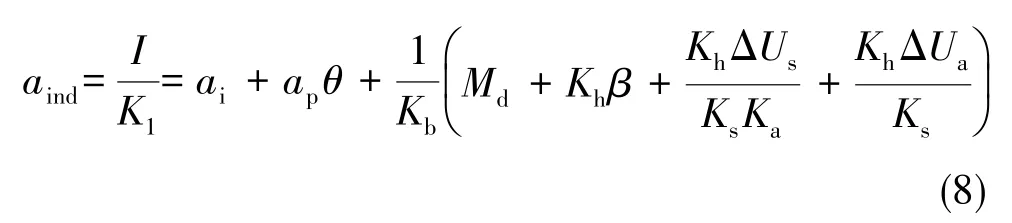
将ai=0、θ=0 代入式（8），可得

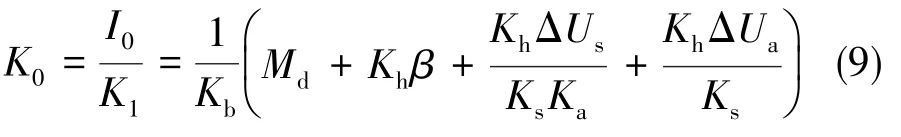
可以看出，影响零位K0的因素包括常值干扰力矩Md、 弹性恢复力矩Khβ、 伺服放大器输入干扰ΔUs和伺服放大器零位输出漂移ΔUa。

加速度计核心敏感器件石英摆片在机械研磨→激光切割→酸铣→镀膜成型加工过程中会产生应力；内部金属结构件采用机械加工方式生产，虽经稳定化工艺措施处理但仍存在剩余加工应力；装配中相互配合的零组件存在尺寸公差和形位公差，使得零件间不可能理想地接触，造成装配后的零组件处于变形状态，引入了应力；石英摆片与其周围接触零件（轭铁及骨架）的膨胀系数不同，在温度变化时会引入热应力。加速度计内部的零组件之间采用胶粘剂进行连接，胶粘剂材料的分子链网络结构及其运动活性受内部影响因素（自身链结构和凝聚态结构）及外部影响因素（温度、应力和物理老化）的影响，会产生蠕变。蠕变是通过分子链段的逐渐伸展或相对滑移实现的，其不仅会造成力学松弛，还会使得被粘接的构件发生相对位移，构件在变形后不能回到原位。加速度计腹带在预紧力作用下通过激光点焊装配，必然会产生焊接变形和残余应力。焊接应力随时间发生释放，使得轴向预紧力发生变化，应力通过摆片外环传递到挠性平桥，进而敏感结构产生偏转，使得偏值发生漂移。以上各种应力在仪表使用过程中随着时间积累而缓慢释放，部分关键环节的应力释放将造成加速度计的偏值产生漂移。

加速度计的力矩器采用了永磁动圈式对顶结构，两个磁路相互独立并形成推挽结构。永磁材料的重复性直接影响着力矩器系数的重复性，进而影响了加速度计标度因数K1的重复性。磁性材料的局部区域存在由热扰动、机械振动、外磁场和地球磁场等产生的磁场，影响了磁性材料的磁状态。这些磁场随着时间会发生缓慢变化，使得磁体内部状态不断调整以达到新的平衡，最终则表现为标度因数K1随时间缓慢漂移。在加速度计磁路中，磁钢与激励环、磁钢与磁极片、动圈与摆片等多个连接处采用胶粘剂进行连接，胶粘剂的重复性缓慢变化会使得敏感质量的质心和电磁力力心发生变化，从而使得加速度计标度因数发生漂移。

在短期内，加速度计的零偏和标度因数在装配完成后，由于以上所述的应力释放和磁性能衰减等因素的影响，会发生较快漂移。前期应力释放受测试环境的影响较快，随着测试周期的加长，应力释放逐步趋于稳定。

4 结论

本文给出了用大样本光纤惯组单次的测试数据评估标定参数有效期的方法，对75套光纤惯组的标定参数进行了统计分析。经评估，标定参数满足有效期要求。实测结果表明，标定长时间后，光纤陀螺标度因数误差、加速度计标度因数误差、加速度计零位误差会发生漂移，其余标定参数无明显漂移趋势。经机理分析，漂移主要是由应力释放和磁性能衰减引发的，随着时间推移，误差漂移趋势会逐渐变缓。本文的机理分析主要局限于定性分析，后续可针对具体原因进一步实现定量分析，并找寻提供参数长期稳定性的方法。