应用于助航系统的赋形曲面光学系统研究

陈 欣， 张志勇， 徐春云， 冯云鹏， 程灏波

(北京理工大学 深圳研究院， 广东 深圳 518057)

基于非成像理论的自由曲面主要应用在照明领域中，实现某种特定形状的照明。自由曲面是指无法用函数解析式来表达、而是由离散点定义并拟合而成的曲面，它是不规则的非对称曲面。自由曲面在非成像光学中的应用，具有体积小、效率高、曲面设计自由度高、出光光形准确可控等优点[1]，可以实现对光能的重新分配。目前，自由曲面设计方法主要有试错法[2]、剪裁法[3, 4]、偏微分方程(Ordinary differential equation，ODE)法[5, 6]、多重表面同步设计(Simultaneous multiple surface， SMS)法[7]、划分网格法[8]，以及其他衍生出的新方法[9-11]。LED作为第四代照明光源具有体积小、寿命长、耗能低、光效高的优点[12, 13]。随着自由曲面的发展，对LED进行合理的二次配光，可使其能够应用于各个照明领域，其中，在航空照明领域内，LED不仅能够很好地解决光源的隐蔽问题，还能够节约能源、减少污染。

根据在机场的用途，滑行道边灯分为嵌入式滑行道边灯、立式滑行道边灯。滑行道边灯必须发恒定的蓝光，灯具必须能为驾驶员提供朝任意一个方向滑行的引导。根据联邦航空局(Federal Aviation Administration,FAA)标准规定，滑行道 边灯的光强分布要求是：在0°～6°仰角范围内的光强至少为2 cd，6°～75°仰角范围内的光强至少为0.2 cd[14]。目前，采用LED光源的滑行道立式边灯多为由若干颗LED镶嵌构成的“玉米棒”形的照明灯具，通过调整LED光源在中间柱体上的摆放位置及数量改变光束角度与光强，满足机场灯具的使用要求。但是，此结构的光束角度与光强不易控制，不得不镶嵌多颗LED以满足光强要求，同时光束较发散，光能利用率低。为了解决这个问题，参考Luo等[11]设计侧边发光的二次配光透镜的思路，本文采用单颗LED作为光源，设计并合理优化了一种侧边发光的二次配光透镜结构。同时，采用这种结构来满足机场助航灯光的立式滑行道边灯的设计要求，使立式滑行道边灯具有结构简单、体积紧凑小巧、单颗LED光源、便于灯具的即刻维修或更换、光能利用率高、耗能低、寿命长、绿色环保等特点。

1 自由曲面的理论模型

通常情况下，从LED光源芯片发出的辐射特性为Lambertian型分布。侧边发光透镜将LED光源发射的大角度的光线进行二次分配，得到沿着光源光轴方向上小角度侧边360°周发光的光能分布，其辐射特性转换如图1所示。为了实现侧边发光的光强分布，侧边发光透镜一般采用全反射-折射自由曲面组合式的旋转对称结构。

图1 Lambertian辐射特性到侧边发光辐射特性的转换Conversion of Lambertian radiation to side illumination radiation

1.1 折射式自由曲面分析

折射式自由曲面可分为凹自由曲面与凸自由曲面两种类型，如图2所示，在直角坐标系中建立折射式自由曲面的理论模型。由LED发出的任意一条光线经过折射率为n1的介质到达自由曲面表面，之后光线根据Snell定律折射到折射率为n2的介质中。由光源S发出的入射光线与垂直坐标轴之间的角度为θ，出射光线与凹的自由曲面的垂直线VV或者凸的自由曲面水平线HH之间的角度为β。假设P(x,y)为自由曲面上的任意一点，直线NN代表P点的法线，直线KK代表P点的切线，P0是折射式自由曲面迭代计算的起始点。i为经过P点的入射角度，i′为相应的出射角度，γ为过P点的切线KK与过P点的水平线HH之间的夹角。根据P点的坐标，可以得到SP的直线方程式(1)：

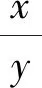
(1)

入射光线在两种介质的交界处的P点发生折射并且满足Snell定律:

n1sini=n2sini′

(2)

由图2(a)得到：

i=θ+i′-β

(3)

γ=i′-β

(4)

通过计算，γ的正切值用式(5)表示：

(5)

P点坐标的微分方程与γ的正切值之间的关系如下：

(6)

对于图2(b)所示的凸自由曲面，其对应的几何光学关系如式(7)、(8)所示：

(7)

(8)

随后，得到该情况下γ的正切值：

(9)

此时，P点坐标的微分方程与γ的正切值之间的关系为：

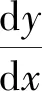
(10)

采用有限差分的方法建立计算方程，即可逐点求出自由曲面上离散点的坐标，差分方程可用式(11)表示：

(11)

式中，(xi,yi) 曲线上第i个坐标点，(xi+1,yi+1)为下一个点的坐标，通过对式(11)的转换可以得到：

(12)

联立公式(1)与公式(12)可以计算出自由曲面轮廓线上各点的坐标。

图2 折射式自由曲面的几何关系(a)凹曲面；(b)凸曲面Geometric relationship of refractive freeform surfaces (a) concave surface; (b) convex surface

1.2 全反射自由曲面分析

类似的，反射式自由曲面同样可以根据有限差分的方法计算出来。由全反射定律可知，光线从高折射率n1介质射入到低折射率n2介质中，并且在分界面上的入射角大于临界角Im时即可发生全反射，临界角可表示为：

sinIm=n2/n1

(13)

如果透镜采用PMMA作为材料，n1=1.49，n2=1代表空气的折射率。经计算可以得到全反射的临界角Im=42.15°。

假设P点发生全反射，i为入射角度，i′为反射角度(如图3所示)，可以得到关系式(14)：

(14)

由式(14)可知，入射角i始终大于临界角Im， 也就是说反射式自由曲面上的每一点都可以满足全反射的条件。

由图3还可以得到式(15)：

(15)

将式(15)带入到式(6)中，通过式(1)、(6)、(12)，可以计算出全反射自由曲面上各离散点的坐标值。

图3 全反射自由曲面的几何关系Geometric relationship of total reflection freeform surface

2 立式滑行道边灯设计

2.1 侧边发光自由曲面透镜模型

侧边发光透镜为旋转对称结构，半个透镜的二维截面曲线如图4(a)所示，该截面曲线由5个部分组成。由LED发射的到达表面1末端的光线与垂直轴线之间的夹角为θ，在这个角度范围内的光线经过内表面自由曲面1折射，得到平行于垂直轴线的出射光线。透镜的第四部分为一个平面反射面，该面与水平轴线呈45°角。透镜的第五部分为一个垂直侧壁。光源出射的光线经过侧壁2折射后到达自由曲面3进行第二次折射。根据第二部分自由曲面的计算方法，建立初始条件为a=3 mm，θ=35°的侧边发光透镜，如图4(b)所示。透镜底部最大口径为14.86 mm，透镜高度为7.21 mm。图5为侧边发光透镜远场的矩形坎德拉分布曲线，在模拟过程中，透镜的旋转对称轴与Z轴方向平行。因此，图5中0截面的光强分布即YOZ平面上的光强分布。90截面是与0截面相垂直的截面，90截面的光强分布即XOZ平面上的光强分布。从模拟结果中可知，侧边发光透镜远场角度分布的峰值光强在侧面方位角为±90°的位置且峰值光强大小为19.6 cd，峰值光强的半峰边角约为6°，侧边发光效率为96.4%。

2.2 立式滑行道边灯结构

基于LED光源的立式滑行道边灯的结构如图6所示，立式灯具离开地面的总高度应不超过350 mm。灯罩的作用是保护内部透镜和电路处 理单元不受外界环境的影响。灯罩的顶部是一个半球形的表面，半球形的底部应与二次配光透镜的底部在同一个水平线上，保证由滑行道边灯出射的光线角度与光强分布不变。上一小节设计的侧边发光透镜，其出射光线方向与水平方向平行，在设计立式滑行道边灯时，将透镜出射角度β设置为0°～6°用来满足FAA的规定标准。由图5的矩形坎德拉光强分布曲线可知，在±80°角度范围内一些光强值为0 cd，不能满足立式滑行道边灯的光强分布要求。因此，可以在侧边发光透镜的顶部周边表面设计两条锯齿来满足大角度的光强分布要求，如图6所示。锯齿的作用是可以使由内自由曲面折射并且经过反射平面反射的垂直方向的小角度光线以相对水平方向成较大的角度出射。VV表示过P点的垂直线，HH表示过P点的水平线，NN表示P点处的法线。i为P点的入射角度，i′为P点的出射角度，δ表示入射光线与水平线HH之间的夹角，δ的最大值δm为6°。入射角应小于全反射的临界角im，也就是说，α的角度应小于(im-δm)。当立式滑行道边灯透镜采用PMMA作为材料，其临界角im=42.15°，因此，选择α为35°来获得相对水平线大角度的出射光线角度。为了便于加工，锯齿齿深w均为0.5 mm，锯齿的出光面与水平方向所成的γ角度为55°。

图4 侧边发光透镜结构(a)二维轮廓线；(b)三维实体模型(a=3 mm,θ=35°)Side illuminating lens structure (a) 2D contour; (b) 3D solid model (a=3 mm, θ=35°)

图5 侧边发光透镜的矩形坎德拉分布曲线Rectangular candela distribution curve of side illuminating lensa=3 mm, θ=35°

图6 立式滑行道边灯结构图The structure diagram of elevated taxiway edge light

3 模拟仿真与实验

为了评价立式滑行道边灯的设计结果，模拟时选用Cree XP-E芯片尺寸为1 mm×1 mm，在波长为0.465 μm下光源的总光通量为15 lm的LED光源。立式滑行道边灯透镜底部最大口径为13.86 mm，透镜高度为7.13 mm。同样采用图5的YOZ坐标系，模拟时透镜的旋转对称轴与Y轴方向平行。由于出射光的角度相对水平方向不再平行，峰值光强角度的位置在垂直方向3°处，其数值大小为8.9 cd，峰值的半峰边角约为11°。垂直方向75°角度范围内，光强的最小值(minI)为0.5 cd。垂直方向上0°位置处的光强(I0)大小为6.7 cd，垂直方向上6°位置处的光强(I6)大小为6.5 cd。由于材料的吸收以及透镜顶端锯齿引起的光能损失，立式滑行道边灯透镜相比第二种类型的侧边发光透镜损失了更多的输出能量，立式滑行道边灯透镜的侧边发光效率为85.4%。立式滑行道边灯的数值模拟如图7所示，水平坐标表示的是透镜垂直方向的角度，垂直坐标表示的是模拟得到的光强数值，红色曲线代表要求的光强边界， 蓝色曲线代表模拟的光强边界。表1为模拟的LED立式滑行道边灯的光强分布与FAA规定的光强分布之间的比较。模拟得到的边界曲线大于规定的边界曲线，本文设计的立式滑行道边灯可以满足FAA规定的光强分布要求。

图7 LED立式滑行道边灯光强分布图The intensity distribution of LED elevated taxiway edge light

图8为立式滑行道边灯实物图：图8(a)所示为灯具整体结构，灯具由顶面为半球形的灯罩和立式支撑架构成；利用注塑成型的方法加工得到的立式滑行道边灯的透镜如图8(b)所示；LED驱动电路处理单元模块如图8(c)所示。测量时光源选用Cree XP-E型号的LED，出射恒定的蓝色光。

表2为测量得到的立式滑行道边灯光强数据，以地面为基准测量垂直地面方向0°～75°且与地面垂直的不同截面的光强分布。垂直方向上0°～6°仰角范围内每隔1°测量一组数据，6°～75°仰角范围内每隔5°测量一组数据。测量结果:不同截面在0°～6°仰角范围内得到的光强最大为9.8 cd，最小光强为4.1 cd，大于2 cd；在6°～75°仰角范围内的最小光强为0.3 cd，大于0.2 cd，与模拟结果接近。由此可知，本文设计的立式滑行道边灯可以满足垂直地面方向0°～75°侧边周发光的光能分布，达到了FAA规定的立式滑行道边灯照明需求。

表1 模拟的LED滑行道立式边灯的光强分布与FAA规定的光强分布的对比

图8 立式滑行道边灯实物图(a) 灯具整体结构； (b) 自由曲面透镜； (c) 电路处理模块Elevated taxiway edge light (a) overall structure of the lamp; (b) free-form surface lens; (c) circuit processing module

表2 立式滑行道边灯光强测量数据

4 总结

本文针对LED点光源非圆对称光斑自由曲面透镜的应用，设计了满足侧边发光的自由曲面透镜。将该透镜结构作为机场助航灯光的立式滑行道边灯透镜的基础结构，同时在透镜的顶部周边表面设计两条锯齿。仿真与实验结果表明，采用一颗LED光源即可满足FAA标准规定的立式滑行道边灯光强分布要求。本文设计的立式滑行道边灯具有结构简单、体积紧凑小巧、便于灯具的即刻维修或更换的优点，也为其他基于LED光源的立式滑行道边灯提供了有效的设计灵感。