单参数Chen 系统的部分状态线性化同步

李德奎

(甘肃中医药大学理科教学部,甘肃定西743000)

1 引言

1990 年,Pecora 和Carroll 首次提出了混沌同步概念并实现了混沌系统的同步[1],为混沌同步的理论研究及应用奠定了基础.近年来,混沌同步得到许多学者的广泛研究,并提出了许多混沌同步方法[2−5].理论上能够实现混沌系统的各种同步,如完全同步、投影同步、相同步等.大多数混沌系统同步就要对其全部状态变量施加较复杂的线性或非线性控制器[6−8],实际应用中混沌同步是较难实现的,主要原因是混沌系统的内随机性和外部不确定因素的干扰,同时系统内部的不确定性和系统的状态变量较多,对其全部状态变量实施控制是不现实的.

为此,设置最简单的控制器,控制尽可能少的系统状态变量,实现混沌系统的全部状态变量同步是混沌同步研究的不懈的追求．刘洪娟等人研究了参数未知的统一混沌系统中的混合同步现象[9],仅通过对一个变量实施线性反馈控制,实现了统一混沌系统同步．然而线性反馈控制要测试反馈增益系数的大小,反馈系数过大或过小都会影响系统的同步.文献[10]基于反馈线性化方法对Rösler 混沌系统的一个变量实施控制,将混沌系统转化为一个线性系统.

文献[11]提出的单参数Chen 系统,该系统结构形式简单,且只含有一个系统参数,同时当唯一的参数a=8 时,系统正的Lyapunov 指数为2.475.因此该系统具有较强的混沌特性,同时电路实现容易,在保密通信领域具有潜在的应用价值.

基于以上讨论,本文根据非线性系统相对阶的概念和Lie 导数运算方法,应用反馈线性化策略,对单参数Chen 系统进行部分状态线性化,同时设计控制器仅对响应系统的一个变量实施控制,实现单参数Chen 系统的同步.

2 非线性系统反馈线性化的条件

考虑一个受控的n 维输入输出系统

式中x=[x1(t),x2(t),···,xn(t)]T∈Rn为系统的状态变量;f:Rn→Rn和g:Rn→Rn为光滑向量场,u ∈R1为系统的控制输入;h:Rn→Rn为光滑的输出函数.

系统(2.1)的反馈线性化问题是寻找坐标变换z=φ(x)和控制器u=α(x)+β(x)v,将系统(2.1)变为线性系统其中v 为变换后的系统控制输入.为了给出系统(2.1)的线性化条件.下面首先介绍相对阶的概念.

定义1设x0∈X,如果存在x0的邻域V 和r ∈Z+,使得系统(2.1)满足下列条件

那么称系统(2.1)在点x0具有相对阶r,其中Lfh(x)=∇hf 为函数h(x)对f(x)的Lie 导数,Lie 导数Lfh(x)是h(x)沿着向量f 方向的方向导数且有

对系统(2.1)的输出y 求导,并根据(2.2)式,得出相对阶r 与输入量u 的关系为

由(2.4)式表明,如果系统(2.1)具有相对阶r,则系统输出的小于r 阶的导数与输入u 无关,只有系统输出的r 阶导数与输入u 有关.若系统(2.1)没有相对阶,则即系统的输出与输入u 无关.

不是所有的系统都可进行线性化,可线性化的系统需要满足一定的条件,下面给出系统(2.1)可线性化的一个充分必要条件.

定理1n 维非线性系统可线性化的充分必要条件是存在一个光滑函数h(x),使得系统

在x0点具有相对阶n.

定理1 给出了系统(2.1)可线性化的充分必要条件,定理1 的证明较复杂,这里不再叙述,证明过程见文献[11].如果定理1 的条件被满足,则存在坐标变换

和系统的控制输入

其中v 是新的输入

将系统(2.1)变为线性系统

3 单参数Chen 系统的反馈线性化

单参数Chen 系统[12]的动力学方程为

其中x1,x2,x3为状态变量,a 是系统参数.当a=32 时,系统(3.1)就演变成了Chen 混沌系统;当参数a=8 时,由Kaplan-Yorke 猜想公式,计算出系统(3.1)的维数D=2.18,说明系统(3.1)具有分数维.此时系统(3.1)的Lyapunov 指数为λ1=−13.23,λ2=−10,λ3=2.22.说明当参数a=8 时,系统(3.1)处于混沌状态,具有如图1 所示的奇怪吸引子.

图1:单参数Chen 混沌系统的奇怪吸引子

将系统(3.1)看作是驱动系统,受控的响应系统描述为

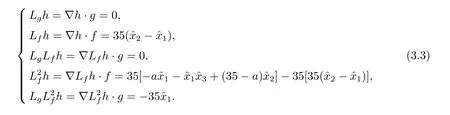
根据系统相对阶的定义和响应系统(3.2)的各阶Lie 导数(3.4)可以看出,响应系统(3.2)的相对阶为r=2.根据(2.6)式,得到响应系统(3.2)的坐标变换为

将响应系统(3.2)部分状态线性化为

下面相应地对驱动系统(3.1)进行线性化,取z1=x1=λ(x),则有

驱动系统(3.1)通过坐标变换

可转化为下列形式

4 单参数Chen 系统的同步

设驱动系统(3.1)和响应系统(3.2)的同步误差为

设驱动系统的线性化系统(3.9)和响应系统的线性化系统(3.6)的误差为

其中K=(k1,k2)的选取使得多项式P3(s)=s2+k2s+k1是Hurwitz 稳定的.

定理2在控制器(4.3)的控制作用下,驱动系统(3.1)和受控的响应系统(3.2)能够实现同步.

证根据(4.2)式,坐标变换后的误差系统为

将(3.6)式和(3.9)式代入(4.4)式可得

将(4.3)式和(4.5)式得

将(3.5)式和(3.8)式代入同步误差(4.1)式和(4.2)式可得

当e1→0、e2→0 时,有从而e3=e−3t→0.综上可得,当t →∞时,ei→0(i=1,2,3),从而在控制器(4.3)作用下,驱动系统(3.1)和响应系统(3.2)实现全部状态完全同步.

5 数值仿真

取参数a=8,此时系统(3.1)处于混沌运动状态,取K=[4,4],初值条件分别为和同步控制器(4.3)重写为

采用四阶龙格–库塔方法,用控制器(5.1)控制响应系统(3.2)的第二个状态变量,所得驱动系统(3.1)和响应系统(3.2)的同步误差曲线如图2 所示.

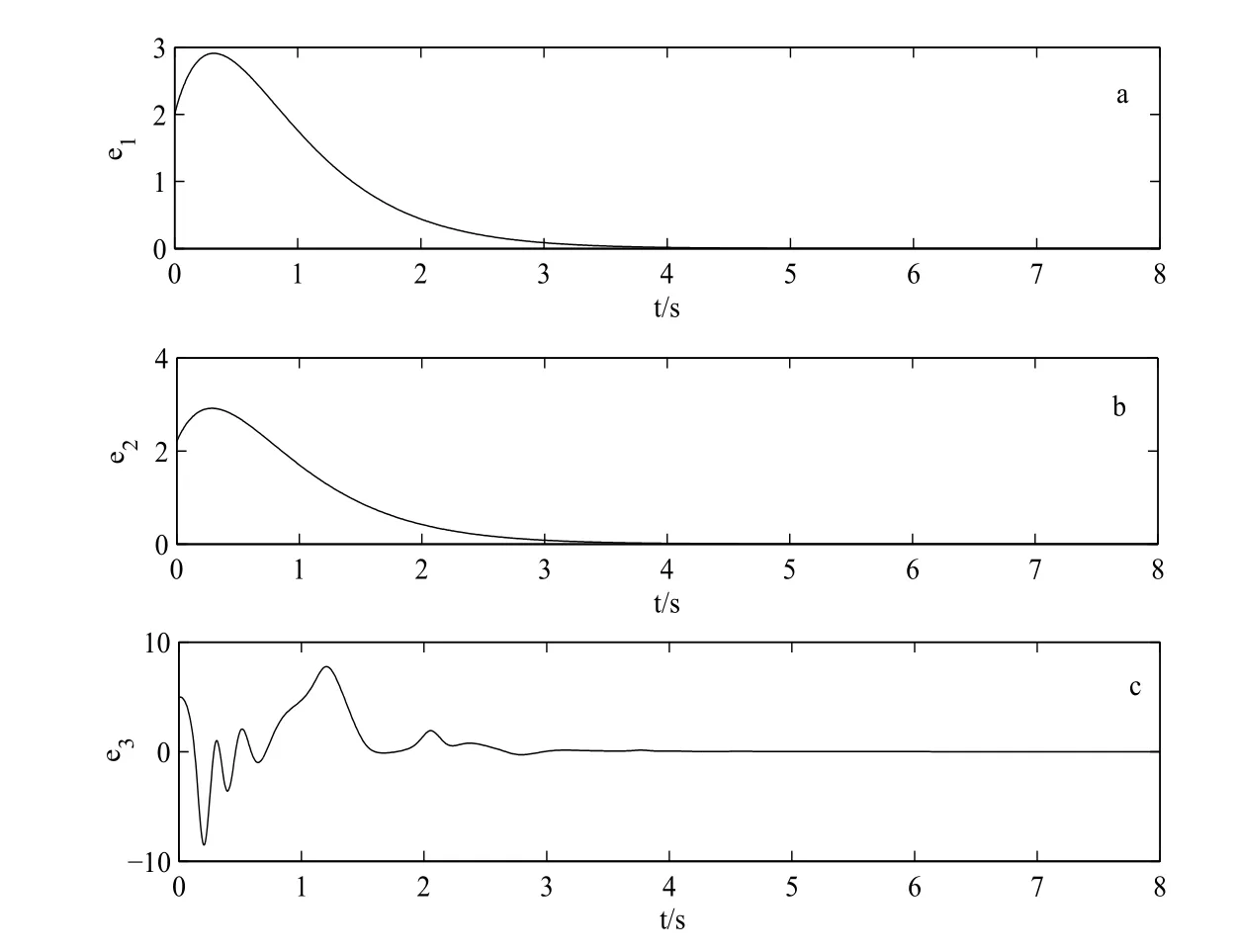
图2:驱动系统(3.1)和受控响应系统(3.2)同步误差曲线图

由图2 可知,驱动系统(3.1)和受控响应系统(3.2)的同步误差ei(i=1,2,3)都快速趋向0,说明利用控制器(5.1)仅对响应系统的第二个状态变量实施控制,驱动系统(3.1)和受控响应系统(3.2)就能快速实现全部状态同步.

在不同初值条件[x1(0),x2(0),x3(0)]=[10,−0.2,0.1]和=[12,2,5]下,在同一坐标系中做出驱动系统(3.1)的状态变量(x1,x3)和受控响应系统(3.2)的状态变量的相图(如图3 所示),其中实线图表示驱动系统的相图,虚线图表示响应系统的相图.

图3:驱动系统（3.1）和受控的响应系统（3.2）的相图

由图3 可知,驱动系统(3.1)和受控的响应系统(3.2)在不同的初值条件下,它们的相图轨线很快趋于重合,说明它们实现了同步.

6 结论

根据任意非线性输入输出系统相对阶的定义,给出了n 维非线性系统反馈线性化的充分必要条件是相对阶r=n.也就是说系统的相对阶2 ≤r

基于状态线性化系统,实现混沌系统同步是混沌同步的研究方法之一.同时,控制尽可能少的状态变量,实现混沌系统的全部状态同步是混沌同步控制的不懈追求.一般情况下,要实现混沌系统的全部状态同步,就要对其全部状态变量实施控制.然而对单参数Chen 系统进行部分状态线性化的过程中,通过对误差系统的分析发现,仅对响应系统的第二个状态变量实施控制,就能实现单参数Chen 系统的全部状态同步,数值仿真也表明理论分析的正确性和同步控制器的有效性,这也是本文的创新所在.当然对于一个可线性化的多参数混沌系统,是否仅对其一个状态控制就能实现其全部状态同步呢?这要通过对误差系统的具体分析来确定.