随机误差对容腔瞬态换热试验影响分析及抑制

丁水汀，邓长春，邱天，*，李江涵，单晓明，贺宜红

（1.北京航空航天大学 能源与动力工程学院，北京100083； 2.航空发动机气动热力国家级重点实验室，北京100083；3.中国航发湖南动力机械研究所，株洲412000）

航空发动机空气系统是处于发动机主流道内侧、外侧的转子与静子或转、静子之间的联系各腔、间隙、流孔的空气流路的总称[1]。广泛应用流体网络法[2-12]计算空气系统压力分布、流量分配等参数。但目前能够计算瞬态换热特性的流体网络法在公开文献中鲜见报道。为弥补这一不足，需开展空气系统元件瞬态换热试验。容腔元件作为典型瞬态元件，是空气系统瞬态换热特性试验的基础研究元件。

国内外相关学者对容腔充放气过程进行过一系列研究。Dutton和Robert[13]开展了单孔容腔充、放气试验，对比了绝热模型和等熵模型的区别，但未研究充、放气过程中的换热特性。Thorncroft等[14]针对单孔容腔充、放气过程，利用模型与试验对比的方法确定多变过程中多变指数，建立了可以预测容腔充、放气过程中腔内压力与温度随时间变化的模型。李世武[15]、马崇扬[16]等对方腔内自然对流换热展开过数值模拟的研究。杨丽红[17]对容腔放气过程进行过数值模拟研究，并建立了热力学模型。郭钟华等[18]针对气动真空系统中容腔，利用“停止法”得出了真空抽吸过程中的换热系数。但此方法对于试验系统控制能力要求较为苛刻，并不适用于大多数类型的试验。丁水汀、于航、邱天[19-20]等利用一种非绝热单孔容腔瞬态响应的零维建模方法，进一步表明非绝热容腔模型较绝热模型能够更精确地反映容腔的真实响应规律，且在10 Hz的数采频率下对非绝热单孔容腔元件充气过程换热特性开展过试验研究，获得了容腔元件的初步换热规律。

由于真实航空发动机空气系统中的瞬态响应时间在毫秒量级，试验中为捕捉更准确的容腔瞬态换热特性，需要提高数据采集频率。在高频状态下，某些试验测试误差会被数据处理的差分过程放大。因此了解试验中换热特性对各种测试参数随机误差的敏感性并掌握有效的误差抑制方法是试验成功的关键。为指导相关试验的开展，本文利用瞬态数值计算结果分析50 Hz数据采集频率下，测试随机误差对试验结果的影响。将利用计算流体力学（Computational Fluid Dynamics，CFD）技术计算所得的非绝热单孔容腔充气过程中满足各守恒定律的数据作为整个充气过程中真实数据。结合试验方案和现有技术水平，对相关数据附加噪声以模拟试验测试随机误差。将利用无噪声数据与有噪声数据算出的换热特性进行对比，分析换热特性误差对不同参数测试随机误差的敏感性。并利用改进经验模态分解（Empirical Mode Decomposition，EMD）[21-23]算法对实验 数据进行光顺处理，降低测试随机误差的影响。本文研究内容对空气系统中其他类型容腔元件的充放气过程换热特性试验的开展均有借鉴意义。

1 相关理论

1.1 物理模型

航空发动机空气系统中的一些腔室结构可抽象为单孔容腔结构[24]。本文将实际航空发动机空气系统内部复杂单孔容腔结构简化为单孔方形腔，其物理模型如图1所示。方形腔边长0.3 m，进气口是一收缩状的喷嘴，处于壁面中心位置。喷嘴进口直径为30 mm，出口直径为10 mm。

图1 容腔物理模型Fig.1 Physical model of cavity

1.2 试验原理及测试方法

单孔容腔充气过程换热特性试验应用的假设与文献[19]中提出的假设相同。实际试验中根据能量守恒方程获取充气过程中的换热特性。单孔容腔在整个充气过程中任意时间段内满足开口系统能量守恒方程：

腔内气体的内能变化量d U等于流进的空气带来的焓值增量d H和腔内气体与容腔壁面的换热量δQ之和。在任一Δt时间段内，d U和d H可以用向后差分的方法近似表示为

式中：cV为空气比定容热容；T（t）为腔内平均温度；cPin为进口空气比定压热容；Tin为进口气流温度；m（t）为腔内t时刻气体质量；Δt=0.02 s。腔内壁面与腔内气体交换的热流密度q表示为

在计算热流密度的过程中，忽略喷嘴进口面积，即容腔表面积A与边长L的关系为：A=6L2。对流换热系数h及平均努塞尔数Nu表示为

式中：Tw为容腔壁面温度；λ为空气导热系数。试 验 中 所 需 测 量 的 物 理 量 包 括L、Tin、T（t）、m（t）和Tw。其 中L、Tin与Tw在试 验中保持 不变，属于稳态测量参数。T（t）与m（t）是瞬态测量参数。

针对T（t）的测量，可以采用响应时间在毫秒量级的高频响热电偶[25-27]。利用流量计测量进口流量随时间变化关系，再进行积分处理可测得m（t）。但在目前的气体流量测量技术中，毫秒级的热式气体质量流量计往往在某些特定的流量下具备快速响应特性，流量测试范围也存在一定的局限[28]。因此试验中难以实现m（t）的直接测量。一种简单的方法是根据理想气体状态方程反推m（t），如式（7）所示：

式中：P（t）为腔内平均压力；Rg为气体常数；V为容腔体积。此方法要求测量P（t）。文献[29-30]介绍的压阻型压力传感器可以满足本文试验频率要求。

1.3 数据样本的获取

样本数据来源于瞬态CFD结果。工质为理想气体。腔内温度变化不大时，忽略物性参数随温度变化的影响。物性参数如表1所示。进口气流温度为295 K，进口绝对压力为191 504 Pa，壁面温度为400 K，进口喷嘴壁面绝热。腔内初始压力为101 325 Pa，初始速度为0，初始温度为295 K。

CFD结果如图2所示。充气初始阶段，P（t）与T（t）快速增高。充气阶段结束后不再有外部气体对腔内进行能量补充，但腔内气体温度低于腔壁面温度，气体与壁面存在换热，T（t）缓慢升高，P（t）变化不明显。根据CFD结果可以确定在此工况下，充气过程大约持续0.68 s，故取0.68 s前的计算数据作为样本数据。

表1 理想气体物性参数Table 1 Physical property parameters of ideal gas

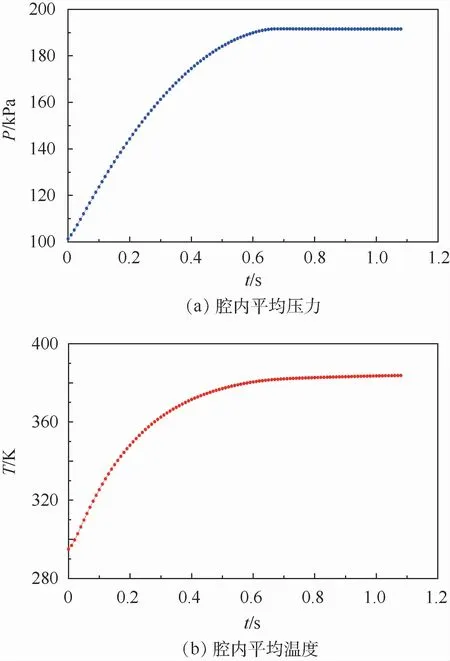
图2 CFD结果Fig.2 CFD results

2 误差分析

2.1 测试随机误差给定

随机误差是试验中难以消除的误差，大小取决于现有测试技术水平。本文试验中随机误差来源于试验件尺寸、气流压力与温度的测量。根据文献[31-39]介绍的高精度加工及测试技术，试验中各测试数据的误差给定如表2所示。稳态测试误差 δL、δTin与 δTw给定为常数，瞬态测试误差δP（t）与 δT（t）按正态分布3σ原则[40]给定。

表2 试验随机误差Table 2 Random error in experiment

2.2 分析结果

定义Nuer为含有误差的努赛尔数，换热特性相对误差百分比δNu为

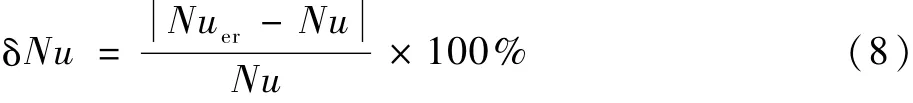
表2给定的常数误差引起的结果误差如图3所示。几何尺寸的测量误差引起的换热特性误差为常数，相对误差只有0.07%。在充气初始阶段的0.02 s内，δTin引起的误差存在误差峰值。因为这一时间段内腔内参数不严格符合集总假设，按照差分的方法算得的d H相对误差较大。在整个充气过程中由于非集总性引起的峰值较小，因此本文不对此进行详细研究。整个充气过程中常数误差引起的换热特性偏差先增后降。这是因为随着充气过程的进行，腔内温度与压力不断升高，对换热误差产生放大效应。到充气阶段后期，腔内压力与温度变化缓慢，进气流量不断下降直至为0。进气流量的减小对误差产生缩小效应。在包含全部单向偏差的状态下，换热特性相对误差在1.80%以内。

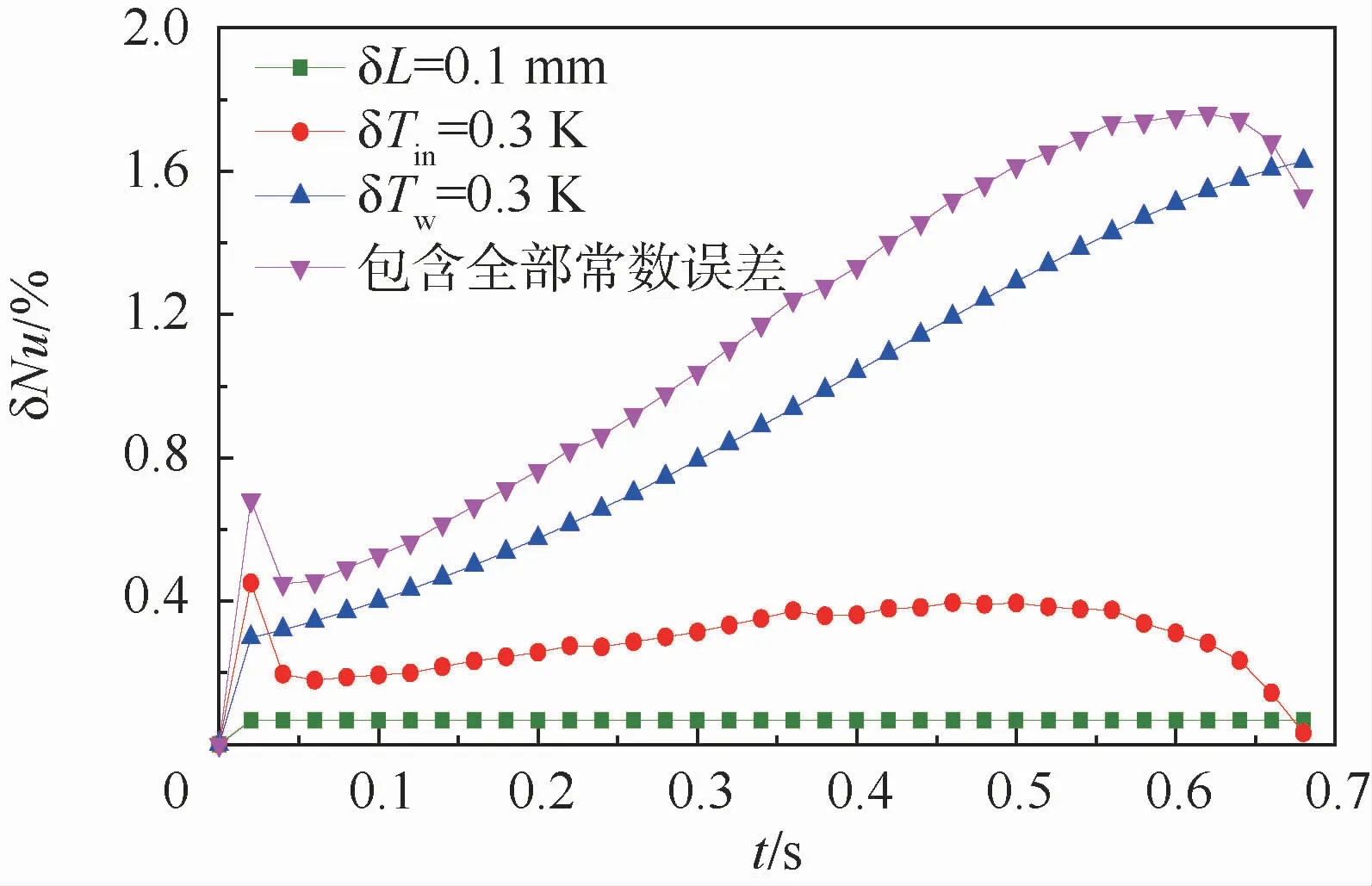
图3 稳态误差对Nu的影响Fig.3 Influence of steady error on Nu

图4给出腔内瞬态相对压力prel测试偏差对换热特性的影响。在充气过程的大部分时间点上，prel测试偏差对换热特性的影响不大。prel偏差在38.78 Pa以内的情况下，换热特性最大相对偏差不到2.00%。

图5给出腔内瞬态温度测试误差对换热特性的影响。腔内温度测试误差对试验结果影响显著，所得换热特性折线图存在大幅波动。温度误差在0.464℃以内的情况下换热特性相对误差最高可达130.22%。

图6展示了腔内温度与压力误差同时存在时的换热特性结果。换热特性波动状态与图5（b）相似，波动幅值较大，最高误差达到129.07%，时均误差为25.24%。可见，腔内瞬态温度测试随机误差对试验结果的影响最为显著，使得试验结果不能准确反映换热规律。

在直接测量的瞬态误差无明显波动状态下，换热特性的大幅度波动表明在数据处理过程中存在误差放大环节。误差放大的环节存在于腔内气体内能增量d U与质量流量m（t）-m（t-Δt）的计算中。波动来源于 ΔP与 Δ（P/T），表达式如下：

图4 压力偏差对Nu的影响Fig.4 Influence of pressure error on Nu

图5 温度误差对Nu的影响Fig.5 Influence of temperature error on Nu

图6 全部瞬态误差对Nu的影响Fig.6 Influence of all transient errors on Nu

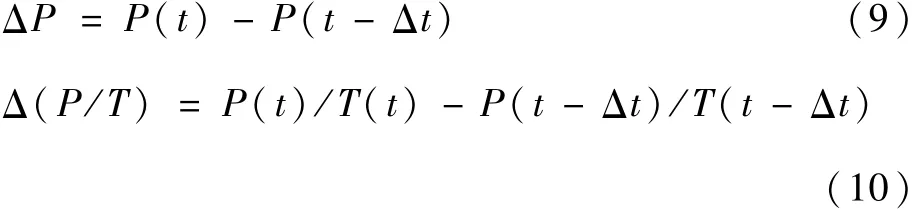
瞬态测试误差同时存在的情况下 ΔP 与Δ（P/T）的计算结果如图7所示。可以发现，ΔP的计算对瞬态测试误差的放大作用不明显，Δ（P/T）影响显著，结果折线图存在较大波动现象。这一波动现象在后续数据处理中会被进一步放大，导致试验结果难以反映实际的换热特性。因此，除了提高测试精度外，抑制 Δ（P/T）的波动也是试验的关键环节。

图7 ΔP与 Δ（P/T）计算结果Fig.7 ΔP andΔ（P/T）calculation results

3 EMD光顺处理

3.1 EMD算法应用

EMD算法对于非线性、非平稳信号的处理具有独特的优越性，其基本原理及信号处理过程在文献[21-23]中有详细介绍。同时此算法对于离散数字曲线具有良好的光顺作用[22]，因此适用于试验数据Δ（P/T）的光顺处理中。

应用EMD算法进行滤波及光顺处理时，处理效果会受到端点效应[16-18]的影响。本文基于极值平移法[18]的基本思想，根据信号端点附近的极值特征，在信号端点后增加两对极值点。具体方法是取0.62～0.68 s的数据，每个数据减去一常数后作为延续信号直接放在原始数据后。极值点的数量、选择方法及被减常数取值不同会对处理结果产生一定影响，本文不重点研究。

3.2 光顺处理效果

利用EMD算法对 Δ（P/T）进行光顺处理的效果如图8所示。应用传统EMD算法对 Δ（P/T）进行处理时，端点效应的影响较为明显。主要体现在充气过程接近尾声时处理后数据存在反常现象。应用改进EMD算法进行处理，端点效应得到有效抑制，Δ（P/T）的波动状态得到了明显的改善。

应用改进EMD算法进行光顺处理后，得到的换热特性折线图如图9所示。改进EMD算法的应用对最终换热特性的结果产生显著改善，换热特性波动幅值明显缩小。在充气过程接近尾声时的换热特性误差较大，最大误差从129.07%降到63.62%，时均误差从25.24%降到8.12%。精度大幅提高，换热特性折线图可反映容腔充气过程近似真实的换热特性变化规律。

图8 EMD算法对 Δ（P/T）处理效果对比Fig.8 Comparison ofΔ（P/T）treatment results by EMD algorithm

图9 改进EMD算法的应用效果Fig.9 Application effect of improved EMD algorithm

4 结 论

针对容腔充气过程换热试验的数据处理过程中差分处理方法放大随机误差的问题，分析了误差放大效应的主要环节并采用改进EMD算法进行误差抑制，得出以下结论：

1）误差放大环节主要存在于进气流量的计算中，此环节将腔内平均温度测试误差放大，影响试验结果。

2）腔内平均温度以外的测试参数随机误差对试验结果影响较小。

3）改进EMD算法的应用可以显著降低试验测试随机误差的影响，在本文研究的工况中，此算法使试验最大误差从129.07%降到63.62%，时均误差从25.24%降到8.12%。