基于最小二乘法和高斯混合模型的语音转歌声算法
段伟博, 朱梦尧, 朱晓强, 王 涛
(上海大学 通信与信息工程学院,上海 200444)
本文研究通过转变说话语音的声学特征来生成歌声.大部分的研究方法[1-3]集中在文本-歌唱合成的领域,这种做法类似于文本-语音合成技术.基于机器学习的语音转歌声方法也很普遍,这种方法[3-4]利用隐马尔科夫模型(Hidden Markov Model, HMM)或者长短记忆序列模型(Long Short Term Memory, LSTM),读取歌声参数,学习其中的音调规律.此外,还有方法通过修改说话语音的声学参数生成歌声.这种使用参数合成歌声的方法需要关注歌声特有的声学参数.目前,许多工作已经研究了歌声所特有的声学特征[5-6]及其听觉效果[7-10],其中最重要的两个声学特征是基频[8,10]和频谱包络[11].通过研究说话和歌声之间的声学差异, 文献[12]提出了基于声学参数修改的语音到歌声的转换算法.这种转换算法简单,且保持说话人的音色,所以将这种方法应用到实际生活中,对用户来说是有趣的体验.例如个别用户不擅长唱歌,文中的歌声合成器可以在不改变原有说话者音质的前提下,将用户自己的声音转换为更好的歌声;或者用户只要知道乐谱的信息,可以任意改写歌词生成歌声.
基于声学参数修改的语音转歌声的算法主要修改语音中的3个声学参数: 基频、语音时长和频谱包络,将说话声音转换成歌唱声音.转换声学参数需要构造各类传递函数,传递函数中的参数影响转换歌声的优劣.目前传递函数的参数是根据研究者试验或者经验给出的,并不适用于所有歌声.本文同样使用基于声学参数修改的语音转歌声的算法,但会利用机器学习的方法来获取传递函数的参数.音乐的多样性造成参数的多样性,本文会在实验中寻找参数的取值规律,这有助于深入了解普通说话的语音与歌声的声学差异,对于研究说话语音和歌声的声学差异具有重要意义,有助于开发计算机音乐作品.
1 语音转歌声算法
语音转歌声算法可以同时记录指定乐谱和说话人的语音文件,其中乐谱提供音乐的节拍、旋律等主要信息.系统从语音中提取所需的声学参数——基频轮廓、时长、频谱包络和非周期性指数,参数按照设计的传递函数分别进行调整.新获得的参数重新合成,得到需要的歌声.算法的流程如图1(第344页),系统对语音参数的调整分为3部分: 语音时长调整、基频调整和频谱包络调整.
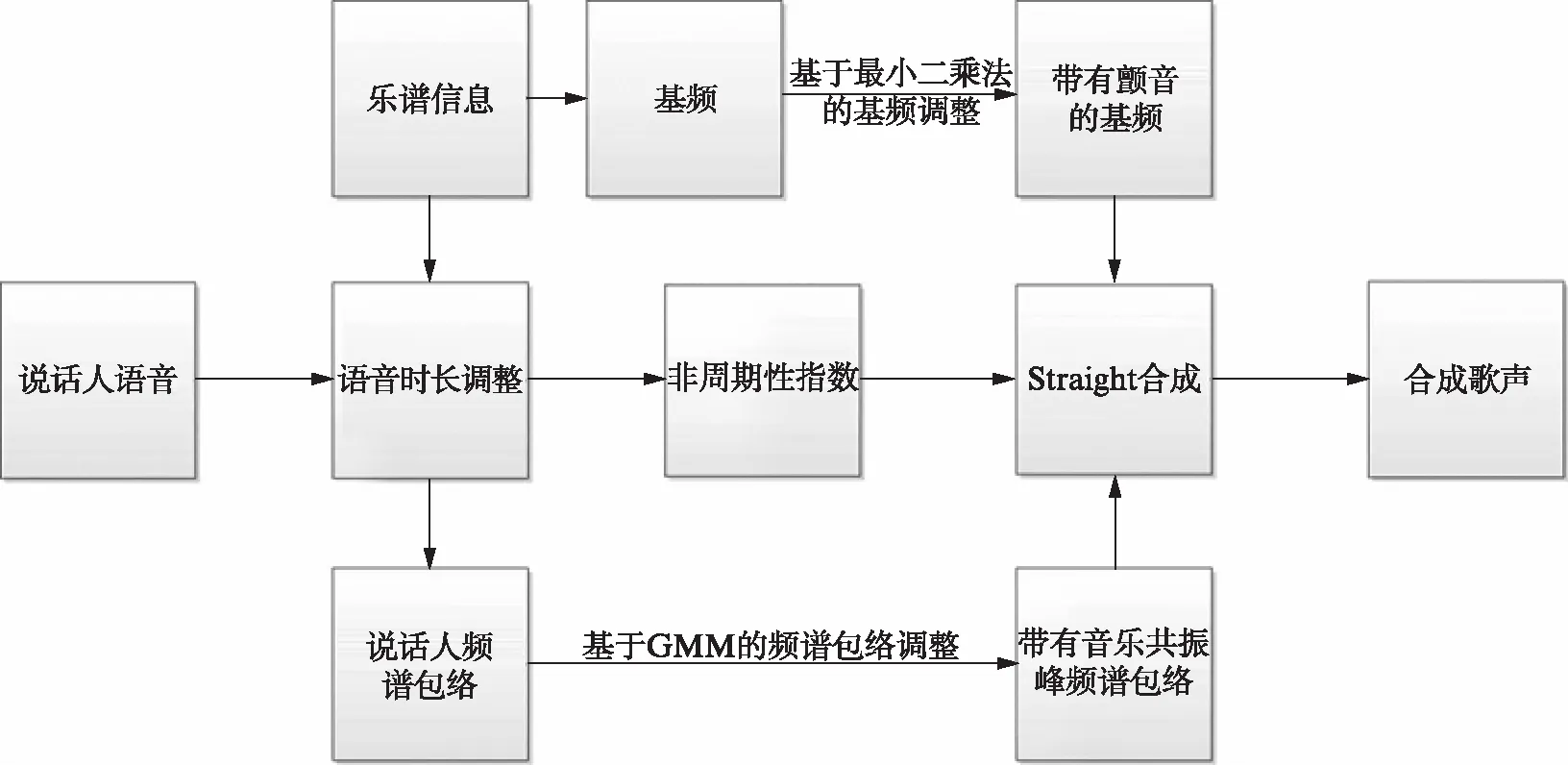
图1 语音-歌声转换系统算法的流程图Fig.1 Flow chart of algorithm for speech-to-singing voice conversion system
语音时长调整较为简单,系统按照相应的音符的持续时间来拉伸或压缩字的持续时间.一般情况下,说话语速较快,通常使用线性插值对波形进行拉伸处理.均匀拉伸的语音帧是以字为单位,同时需要对语音帧进行预处理,即对每个字的时域波形的首末位置补零.预处理的目的主要是消除波形的跳变,形成过渡,减少噪声.
下面重点对基于最小二乘法(Least square method)的基频调整和基于GMM的频谱包络调整进行介绍.
1.1 基于最小二乘法的基频调整
普通说话语音和歌唱声音主要差异在于基频的不同,文献[12]证明了基频特征在音乐转换中的作用大于频谱特征.基频代表说话人声带每次开启和关闭的时间间隔,反映了声调的变化.基频的大小取决于声带的大小、厚薄、松紧程度以及声门上下之间的气压差的效应等.我们利用World分析法获取基频,过程分为3步:
1) 使用不同截止频率的低通滤波器进行滤波,如果滤波后的信号只包含一个周期的信号,即为基音周期,由于基音周期未知,算法会使用多个不同截止频率的滤波器去滤波;
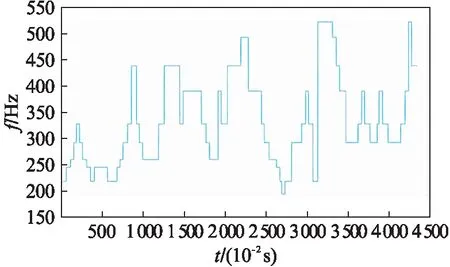
图2 《潇洒走一回》的乐谱基频Fig.2 Music fundamental frequency in “Walk Gracefully Once”
2) 计算基频候选以及置信度,取4个周期,计算每个周期的过零率、峰值、各个斜率对应的区间,理论上4个周期波形所对应的3个参量一致,所以以此为标准计算置信度;
3) 选取置信度最高的频率作为最后的基频.
当将说话声音转换为歌唱声音时,丢弃说话声音的基频轮廓,使用歌曲的音频来替代生成歌唱声音的基频轮廓,图2为《潇洒走一回》的乐谱基频.因此说话人语音的基频按照如图2所示的基频进行修正.
如果使语音基频等于对应音符的频率,合成的歌声不会存在颤音,导致歌声自然度降低.为了提高合成歌声的自然度,文献[12]提出合成基频轮廓应具有局部基频波动变化(图3),这类波动包含在各种歌唱声音中,并影响歌唱声音的听感.根据基频的变化,本文可以将基频分为两部分处理,基频的跳变区[13-14]、基频的平稳区[15].在传统方法中,这两个部分的波动都是通过一个2阶系统的传递函数[12]来实现:
(1)
其中:ω是自然频率;λ是阻尼系数;k是系统的比例增益.式(1)所表达基频图谱的修正如图3(a)所示,(b)中蓝线为某歌手歌唱时的实际基频,颤音的存在造成(b)与图2之间的差异,(c)为实际歌声某一区间上的频谱图.
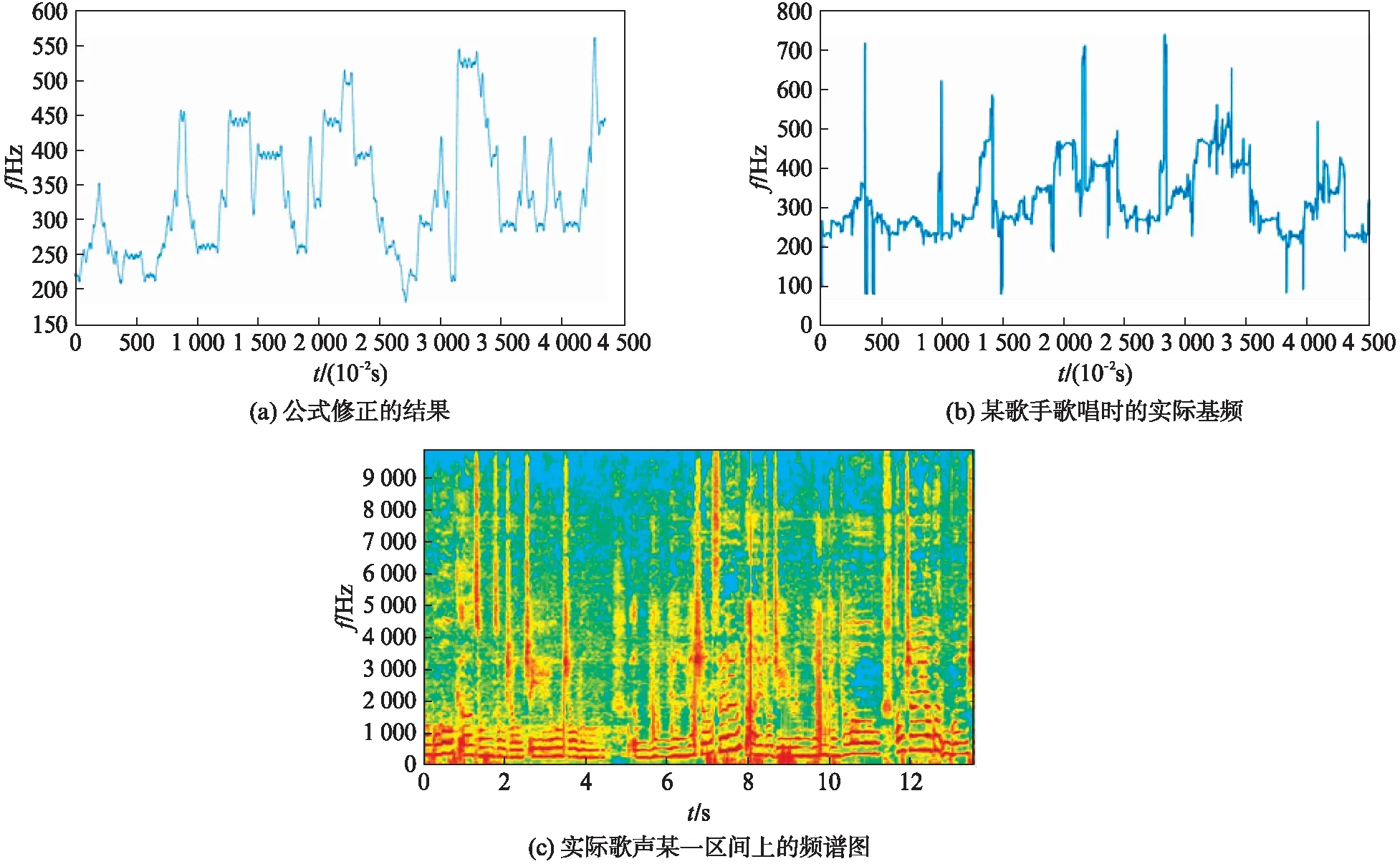
图3 《潇洒走一回》带有颤音的歌声基频Fig.3 Singing voice fundamental frequency with vibrato in “Walk Gracefully Once”
式(1)的参数ω,λ,k影响颤音的振荡衰减区间和振荡幅度,其中ω影响波动衰减的快慢,k为波动的幅度,传统的基于声学参数修改的语音转歌唱的算法[12]的ω过小,颤音的振荡衰减区间过小,频谱和听感上很难体现颤音的效果.本文尝试用机器学习的方法寻找合适的参数.
式(1)作用在频域上: 在平稳区构造三角函数拟合颤音;在跳变区构造带有衰减的三角函数拟合颤音.基于此构造时域上的公式:
(2)
其中:f0为乐谱的基频;f0_system为合成音乐基频;k1,k2对应式(1)中的k;ω2对应式(1)中的ω;ω1决定基频跳变区所产生带有衰减正弦信号的衰减速度.当f0_music是目标音乐的基频时,目标函数为
(3)
式(2)的函数形式为曲线,式(3)非常适合用非线性最小二乘法去寻找最佳参数.拟合曲线的损失函数如下:
(4)
其中:N代表切分的基频跳动区和基频平稳区数量;T代表切分区域内基频采样点数量;τ为切分区域内的基频采样点距离所在区域起始位置的时间.通过机器学习中最小二乘法来最小化损失函数,最终获得最优的参数的组合,用于拟合歌声基频的实际颤音.式(4)非线性最小二乘法不能像线性最小二乘法那样用求多元函数极值的办法来得到参数估计值.考虑到波动的周期性以及衰减函数存在唯一最大值,系统使用搜索算法计算未知参量,先利用最大值估计出k1和k2,再利用周期估计出ω2的取值,然后固定这3个参量,去搜索计算ω1.最后通过ω1去搜索上面3个参数,依次迭代,直到收敛.
1.2 基于GMM模型的频谱包络调整
系统通过修改语音的频谱参数生成歌音中带有特定峰值的频谱包络.文献[9]表明,歌唱声音的频谱包络在3kHz附近有一个叫做“歌唱共振峰”的显著峰值,文献[8,16-18]的研究证实了这种类型的声学特征包含在各种不同的歌声中,影响着人们的听感.
World分析法通过CheapTrick方法获得频谱包络信息.语音按照基频的周期为单位进行分段,以此保证波形和频谱的平滑连续.对于加窗以后的时域信号进行傅里叶变换获得对应的频谱,然后在三角窗内对信号进行平滑,再利用倒谱方法,求取频谱的包络信息:
F(f)=exp(F[ls(τ)lq(τ)ps(τ)]),
(5)
其中:ls(τ)为低通滤波器;lq(τ)为消除平滑造成的畸变;ps(τ)为倒谱.在倒谱中,频谱的包络对应着倒谱的低频信息.根据文献[9,12]增加谱包络在3kHz的能量,
Fmusic(f)=W(f)F(f),
(6)
(7)
其中:F(f)是说话人的频谱包络;W(f)是设置的权重函数;Fs是本文关注的3kHz;k为系统设置的增加权重;Fb为人为设置的带宽,根据共振峰衰减情况,这个值较大,区间为1kHz~2kHz.
式(6),(7)是一种简单的加权函数,作用的频域范围单一.频谱包络只在3kHz位置处生成音乐共振峰,但实际中,共振峰只是出现在3kHz附近的区间.式(6),(7)无法动态地调整共振峰位置.本文利用高斯混合模型(GMM)建模,去学习频谱包络的变化规律.我们在第t帧获取说话人语音的频谱包络信息xt=[xt(1),xt(2),…,xt(Dx)]和歌声的频谱包络信息yt=[yt(1),yt(2),…,yt(Dy)],用GMM建模,得
(8)
其中:z是表达为zt=[xt;yt]的联合向量;α是GMM中各个高斯分布所占有的权重;均值向量和协方差矩阵
(9)
使用期望最大化(Expectation Maximization, EM)算法去训练GMM.利用训练后的GMM,在已知说话人频谱包络的情况下可以用最大似然估计求取我们需要的音乐频谱包络:
(10)
构造辅助函数[19]
(11)
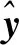
2 实 验
这部分内容研究语音转歌声系统,包括系统参数的计算和合成歌声的评估.
2.1 实验参数
实验选择阿卡贝拉的歌声库Dataset_Chitralekha_ISMIR2018和发布的中文清唱用于分析歌声系数.根据计算和分析,因为音乐本身具有多样性,个人的唱法也对歌声参数有极大的影响,因此用单一的参数描述歌声声学特征是不够的,表1为式(2)中基频跳变区中部分参数的取值规律.

表1 基频跳变区的参数
歌声参数复杂多样,本文尝试从音乐种类和音频变化趋势来寻找规律.从表1可以看到,k取值范围较大,但是取值范围和基频跳变的幅度有一定的关系,整体上成正相关;对于ω2,参数的取值主要和歌曲类型有关,歌声越轻缓,ω2越小.因此基频跳变幅度和歌曲类型对我们设置参数有一定的指导作用.
图4给出了式(2)拟合2.5ms基频平稳间内的颤音的情况,纵轴为基频频率f(Hz),横轴为时间轴,黑点w为歌声的采样点,蓝线为拟合的函数曲线,其中图4(a)只使用了一个函数,图4(b)中使用了2个函数拟合区间上的2个片段.
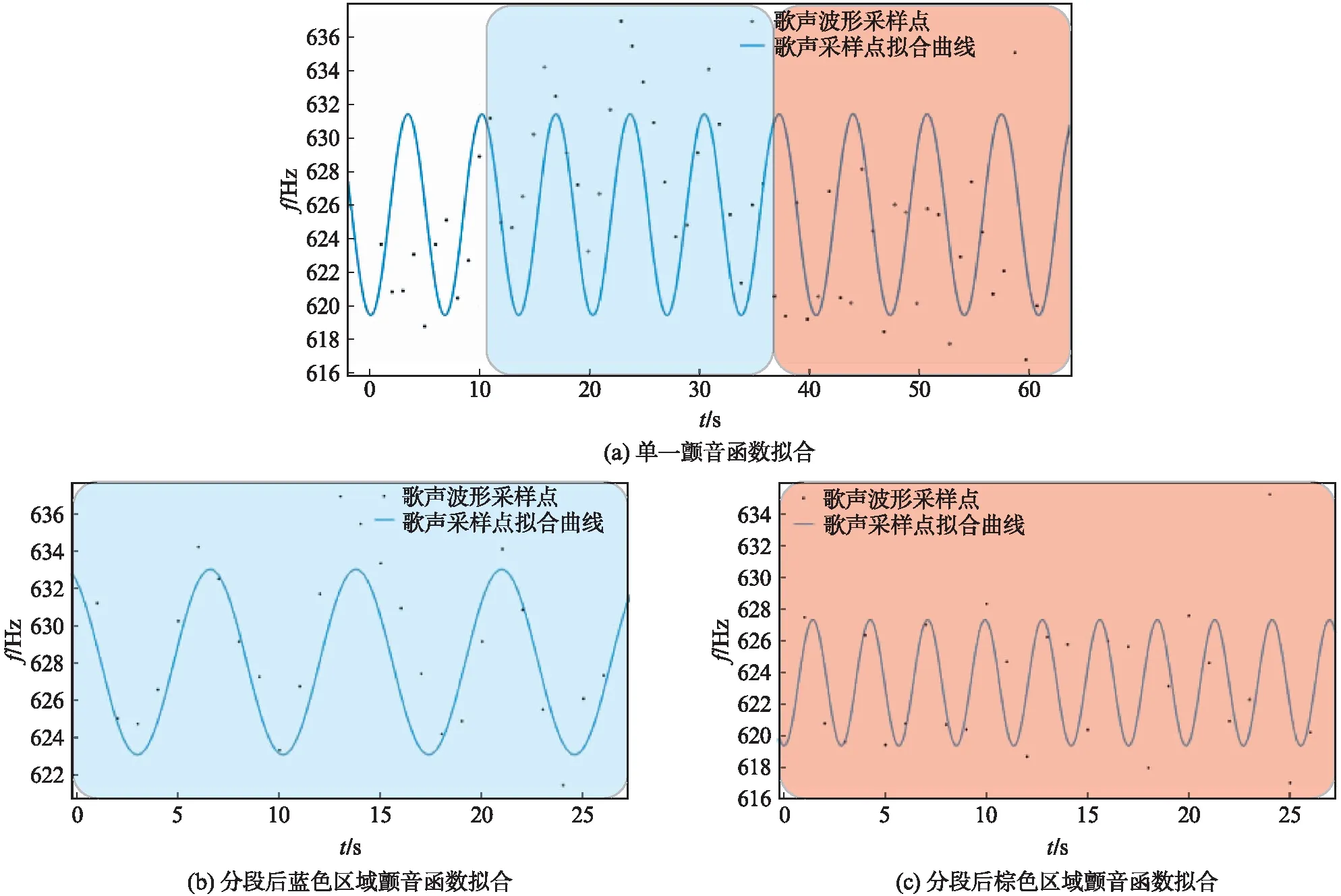
图4 式(2)拟合2.5ms基频平稳间内的颤音Fig.4 Formula (2) fitting tremolo in 2.5ms fundamental frequency stationary interval
如图4(a)所示,很多采样点并没有坐落在拟合函数的曲线上,造成较大的误差.当对语音帧分段,每段语音分别进行函数拟合,拟合误差将得到改良,如图4(b),(c),大部分点都坐落在拟合曲线上.函数拟合歌声的颤音可以视为多个不同的正弦波拼接而成,颤音的参数在不同的时间段内是不同的.这说明传统方法用单一的颤音参数进行歌声合成是不够的.本文使用分段函数来拟合,可以增加歌声的多样性,以求更真实的表现歌声的形式.
2.2 评 价
实验中,听众分别去听真实歌声与合成歌声并进行评价.合成版的歌声包括2种: 一种为传统滤波器方法合成;另外一种为我们方法合成的.例如对《潇洒走一回》,式(2)设置参数如下:
k1=|f0t-f0t+1|×2e-0.01|f0t-f0t+1|(Hz),
(12)
k2=7.5±2.5(Hz),
(13)
ω1=5±3(rad·ms-1),
(14)
ω2=8±1(rad·ms-1),
(15)
其中:f0t为乐谱当前节拍的基音频率;|f0t-f0t+1|代表当前节拍与后一节拍的跳变值.与真实歌声相比,2种方法合成的歌声的自然度相同,但仍然到不了真实水平,这是基于修改普通人说话语音的频谱系统的局限性.说话语音和歌声的激励方式不同,说话语音的音质较差,生成的歌声听感也差;在对频谱进行修改时,谱颤音变化在高频谐波部分集中体现,通过机器学习获得的实验参数和实际歌声声学特征必然存在误差,但即使只有较小的偏差,在高频谐波部分就会放大,歌声不自然度就会提高;同时利用GMM转换存在过平滑的问题,这影响频谱轮廓的生成.所以基于修改频谱的语音转歌声系统仍然需要改进.
虽然2种合成歌声自然度相同,但本文方法合成的歌声在个别时间段(图5的黑色框图标示区域)可以很好地仿真歌手带有颤音的歌声,同时在其他区间又和传统方法相对缓和,这说明我们的方法可以实现合成歌声的多样性.从频谱图(图5)可以观察到本实验合成歌声与传统方法合成歌声的差异,两者能量分布在大部分区间上基本一致,橙色越深,能量越高.其中蓝色区域属于频谱能量极低的区域,这是按照节拍调整说话语音所产生的静音帧.但本系统考虑了前后音节差值,图5的黑色框图标示区间能量的分布出现差异.在黑色框图标示区间内,图5(a)中能量波动剧烈,反应出颤音衰减幅度大;而图5(b)中颤音幅度和其他区间相近,生成的颤音很少.与图3(c)的实际频谱图相比,我们方法的频谱图更为接近,既有谱线振荡剧烈的区间,也有谱线相对平稳的区间.
除了表现歌声多样性,本文还重点关注歌声的声学参数.本实验通过机器学习的方式得到多组参数,利用多组参数组合去合成更真实的频谱,用来提高歌声的听感.由于音乐的多样性,需要根据不同情况进行分析,例如音乐种类和音乐基频变化幅度,甚至还有听众自身的喜好.虽然参数具有多样性,但通过寻找规律,仍然可以确定歌声参数所在的区间.实验发现,歌声的种类与颤音震荡周期有关,在构造滤波器时,音乐越舒缓,式(1)中的ω2越小,这样系统可以表现更真实的音乐基调;颤音的衰减幅度与前后音节有关,设置的参数k需要和前后的音节差值成正相关,这样频谱中的音节过渡更真实.

图5 2种方法合成歌声的频谱图Fig.5 The spectrogram of composite songs by two methods
实验并没有使用主观评分的方式判断合成歌声的优劣,而是利用听众评价的方法,这样可以根据听众的评价来寻找更多歌声参数的规律.例如听众反映以e、o元音结尾的歌词在没有颤音的情况下,听觉效果更佳;也有听众反映长节拍的音素使用振幅更大的颤音会有更好的效果.这说明除了旋律、音色等因素,音素也对合成歌声也有极大的影响.
本文通过寻找歌声参数规律可实现歌声一定的多样性,但在实际中还有更多需要关注的部分,这是今后的研究方向.
3 结 语
综上所述,本文设计了一种基于机器学习的语音转歌声的合成系统.该系统通过机器学习训练出传递函数的参数,然后利用学习后的转换函数修改语音的声学特征,包括基频和频谱包络,并延长语音时长,将语音转换为歌声.实验结果表明: 系统能够合成出较好的歌唱声音.系统的算法简单有效,可实现音乐一定的多样性,这大大提高了系统的实用性.
未来的工作还将继续改善语音转歌声算法:
1) 理想情况下,我们希望输入一段完整的语音进行处理,这样可以简化用户的操作.但目前我们使用的仍然是切分的语音.主要是因为目前没有简单的方法进行语音切分,仅靠语音端点检测效果完全不可行,这反而要涉及更复杂的语音检测或语音识别.所以目前合成器应用只局限在可切分的语音.
2) 记录每个节拍的长度也大大降低了合成器的实用性,因为音乐的节拍不固定,难以找到规律,所以目前系统只能人为固定歌词的节拍.后续工作中,我们会通过机器学习的方式学习到歌词对应乐谱的位置, 考虑到这是时间序列的计算,理想的模型有HMM和LSTM.
3) 基频的调整使用非线性最小二乘法的搜索算法,效率较低.我们需要寻找更好的算法或者构造更简单的数学公式去拟合.
4) 系统整体设计思路的改进.从程序的算法上来看,这类似一个数组的拼接过程.如果一个节拍计算出现错误,后面所有的节拍会全部出错.将来会引用类似标签的方式,将歌词固定在它所在的节拍上,从而提高系统的容错率.
5) 系统并没有改变一个人的音色,但考虑到普通人在音质上仍然低于歌手,我们希望将来的工作修改这一问题,对用户的音色进行修正.

