计及分布式电源的配电网双层优化重构

(兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070)

随着传统化石能源的逐渐短缺和环境恶化问题的日益严峻，可再生能源的开发和利用变得日益重要。以风电、光伏为代表的分布式电源(distributed generation,DG)大规模接入配电网可以有效缓解能源紧张，向用户提供绿色电力，是电力系统实现“节能减排”的重要发展方向[1]。由于分布式发电具有污染排放低、灵活方便、效率高等优点，能够增强配电网抵御自然灾害和各种风险的能力，因此应提倡分布式发电并网，以加快各种形式的分布式能源的发展。然而，DG出力具有较强的随机性和间歇性，DG接入配电网使系统的复杂性和不确定性增加，如潮流方向、网络损耗、支路功率等都会产生较大的变化，对配电网的安全、可靠运行带来不利的影响。研究表明，DG接入配电网的位置和容量对配电网网损和电能质量有重要影响[2]。

配电网自动化已经成为配电网发展的主要方向，配电网重构是其中的一个重要内容，是城乡电网改造必须考虑的重要问题，也是配电网安全、经济运行的重要保证。配电网重构于1975年由Merlin等[3]首次提出，是指在满足配电网运行约束条件的前提下，通过改变配电网中各节点分段开关和联络开关的状态，以达到改变网络拓扑结构，实现配电网优化运行的目的，是提高配电系统安全性和经济性的重要手段。

近年来，国内外学者对含DG的配电网重构进行了大量深入研究，为后续的应用积累了一定的经验。文献[4-5]中均采用有功网损最小的单一目标函数优化配电网，但未考虑多目标函数优化的问题。文献[6-8]中主要改进配电网拓扑结构简化方法，使其尽量避免不可行解的生成。上述文献中DG容量和位置都是事先假定的，并没有考虑DG安装位置与容量对配电网重构的影响。文献[9]中将配电网重构与DG功率配置作为非线性优化问题，并采用人工蜂群算法以实现配电网优化重构。文献[10]中采用一种分步启发式算法和灵敏度指标，实现了配电网重构与DG功率分配共同优化。上述文献虽然考虑了DG出力对配电网重构产生的影响，但是未将DG安装位置计入优化过程，具有一定的局限性。文献[11-12]中只是将DG优化配置作为简单的初始条件进行配电网重构，但是未将DG安装位置和容量与配电网重构之间相互制约的关系体现出来。

针对上述配电网重构研究方法存在的局限性，本文中提出一种计及DG容量与位置的配电网重构双层优化模型。该模型将DG安装位置和容量作为上层优化目标，将配电网重构作为下层优化目标，上下层模型优化结果相互制约，进而确定出最优的网络结构和最佳的DG安装位置及容量。其中上层优化模型以电压稳定性指标和DG并入配电网产生的网损变化量作为目标函数进行优化，下层优化模型以有功网损和负荷均衡度作为目标函数进行优化。

1 配电网重构数学模型

1.1 上层目标函数的建立

1.1.1 DG位置的确定

DG接入配电网会对系统的节点电压产生不可忽略的影响，电压会随着DG位置和容量的变化而变化。为了使DG的位置和容量达到最优，进而使系统电压可靠性得到提升，应该合理地配置DG。电压稳定性指标(voltage stability index，VSI)反映了电力系统的电压稳定状况，其值的大小反映了母线电压稳定度的优劣，因此，本文中采用VSI来确定DG的安装位置。假设有一条支路k，如图1所示，电压稳定性指标的数学表达式[13]为

(1)

式中：Pl,i+1、Ql,i+1分别为流入节点i+1的有功功率和无功功率；Rk、Xk分别为支路k的电阻与电抗；Vi为节点i的电压。

Pl,i+1、Ql,i+1分别为流入节点i+1的有功功率和无功功率；Rk、Xk分别为支路k的电阻和电抗；Vi、Vi+1分别为节点i和i+1的电压；Ik为支路电流。图1 简单配电网典型支路

根据VSI的相关知识，DG并入配电网的位置以电压稳定性指标变化量最大为目标函数来确定，将其标幺化，表达式为

f1=ΔYVSI=max(1-YVSI,i),i=1,2,…,Nbus,

(2)

式中Nbus表示系统的结点数。

通过潮流计算可求得VSI值，将所得VSI值按照递增的顺序排列，其值决定了节点配置DG的顺序。若VSI值越大，则相关节点的稳定性越好，不需要接入DG；反之，节点的稳定性越差，需要通过接入DG来改善母线电压稳定性。

其约束条件为

(3)

1.1.2 DG容量的确定

DG并入配电网会使潮流方向发生改变，从而影响电网电压分布，因此接入DG容量的大小对系统网损产生的影响不可忽略。由于大多数文献中并未考虑DG并入配电网后网损的变化，因此本文中将网损计入目标函数，用于确定DG并入配电网的容量。如图2所示，假设有一条首、末节点为i和i+1的支路k，将DG接入系统任意一位置，则系统并入DG后的网损[14]可表示为

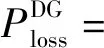
(4)

DG并入前、后的网络损耗减少量可表示为

(5)

式中：Pk、Qk分别为流出节点i的有功功率和无功功率；PDG、QDG分别为DG向配电网提供的有功功率和无功功率；Rk为支路k的电阻；Vi为节点i的电压；G为根节点与并入DG节点之间的距离；L为根节点到负荷节点i之间的距离。

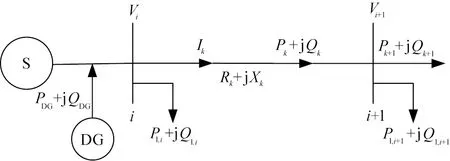
S为系统电源；DG为分布式电源；Pk、Qk分别为流出节点i的有功功率和无功功率；PDG、QDG分别为DG提供的有功功率和无功功率；Pl,i、Ql,i分别为流入节点i的有功功率和无功功率；Rk、Xk分别为支路k的电阻和电抗；Vi、Vi+1分别为节点i和i+1的电压；Ik为支路电流。图2 并入分布式电源的简单辐射性线路

(6)

其约束条件为

(7)

上层优化模型由式(2)、(6)构成。因为DG位置和容量与配电网重构存在相互制约的关系，即DG位置和容量的变化将会作用于配电网重构，同时，配电网拓扑结构的不同也会改变DG位置和容量，所以可为下层优化模型的优化提供初始条件。

1.2 下层目标函数的建立

下层优化模型采用配电网中系统网损和负荷均衡度作为网络优化目标函数，将其应用于配电网重构优化中。假设有一条支路k的首末节点分别为i和i+1，如图3所示，该支路的网损可表示为

(8)

整个网络在配电网重构前的总网损Pt,loss的数学表达式为

(9)

式(8)、(9)中：Pk、Qk分别为节点i注入的有功功率和无功功率；Rk为支路k的电阻；Vk为节点k的电压。

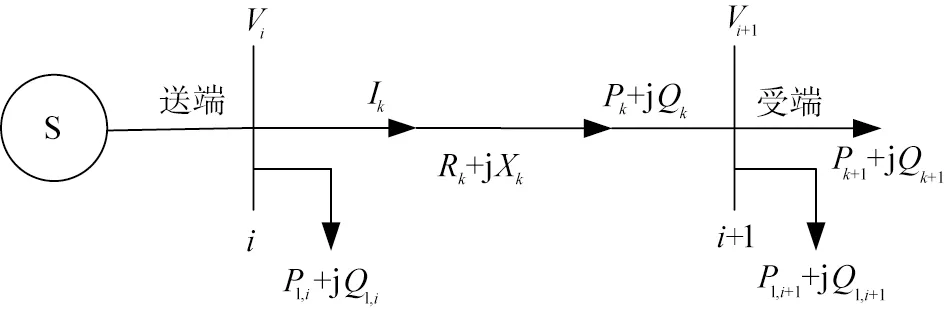
S为系统电源；Pk、Qk分别为流出节点i的有功功率和无功功率；Pl、Ql分别为流入节点i的有功功率和无功功率；Rk、Xk分别为支路k的电阻和电抗；Vi、Vi+1分别为节点i和i+1的电压；Ik为支路电流。图3 重构前的简单辐射性线路

同上，配电网重构后支路k的网损为

(10)

(11)

(12)

配电网重构是一个非线性、多维数、多约束的多目标优化问题，本文中从经济性和可靠性2个方面综合考虑构建配电网重构的目标函数，使其更具有实际意义。

1)从经济性方面考虑，目标函数以网损减少量最大为目标函数，将其标幺化，数学表达式为

(13)

2)从可靠性方面考虑，以系统的负荷均衡度变化量最大为目标函数，其数学表达式为

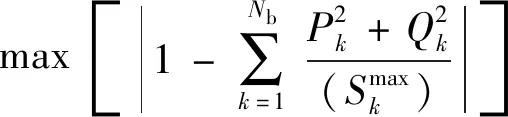
(14)

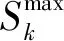
负荷均衡度与网损并非简单的正相关，即负荷均衡度达到最优时，网损并非最优，反之亦然，因此下层优化模型以网损和负荷均衡度为目标函数，其数学表达式为

F=max(f3+f4)。

(15)

其中配电网重构满足下列约束条件。

1)潮流约束。

(16)

式中：Pi、Qi分别表示向节点i(i=1,2,…,Nbus)注入的有功和无功功率；Vi、Vj分别表示节点i和节点j的电压；Yij分别表示节点i与j之间的导纳；δi、δj分别表示节点i、j的电压相角；θij表示节点i、j之间的导纳角。

2)节点电压约束。

(17)

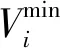
3)支路电流约束。

(18)

4)网络拓扑约束。

在配电网重构前、后，网络结构始终保持辐射状，即gk∈G，其中，gk表示重构后的网络结构，G为所有可行的辐射状网络的集合。

2 重构环编码原则

配电网中包括2类开关，分别为大量的分段开关和少量的联络开关。配电网的运行方式为闭环设计、开环运行。根据运行方式可知，闭合一个联络开关，网络即可构成一个基本回路，而断开回路中的任意一个分段开关，网络即可保持辐射状运行，因此采用合理的编码方式，可有效减小搜索空间，提高寻优效率。

基本环可定义如下：配电网中的一个联络开关和若干分段开关构成的一个回路即为配电网的一个基本环。根据其定义可知，配电网中联络开关的数量即为基本环的数目。本文中采用IEEE 33节点配电网，如图4所示，根据上述相关知识可知，33节点配电网包括32个分段开关和5个联络开关，故含有5个基本环。

图4 IEEE 33节点配电网接线图

2.1 配电网拓扑简化

配电网重构时，联络开关的数量等于解向量的数量，每个解的维数等于基本环开关的总数[15]。传统的编码方式采用二进制编码规则，数值1代表开关闭合，数值0代表开关打开。随着配电网拓扑结构复杂程度的增加，解的维度会随之增加，搜索空间将以几何级数骤增。以IEEE 33节点系统为例说明，33节点网络共有37个开关，其中包括32个分段开关和5个联络开关，其搜索空间则为237种状态。虽然有很多种开关状态；但是在所有的开关状态中包含大量的不可行解，严重影响寻优的速度和质量，因此对配电网的拓扑简化至关重要。

根据图论的相关知识及配电网的结构特点，网络的拓扑简化原则可总结为以下3点：

1)直接与电源节点相连的支路不编码。

2)对于不形成回路的独立支路，若断开开关则会形成孤岛，故不对其进编码。

3)利用图的节点度的相关知识可知，闭合网络中的所有开关，将入度d+(x)与出度d-(x)之和小于等于2的所有节点间的支路融合为1条支路，该支路记为1个支路组，两者可相互等效。

2.2 不可行解的修正

对于不可行解，主要有以下2种方式对其进行修正：1)采用有效的编码规则，控制解向量生成原则，进而减小产生不满足约束条件的解向量的概率；2)利用相关策略提高判定约束条件的效率，进而提高产生可行解的速度。本文中采用第1种策略进行不可行解的修正，具体修正策略为：

1)每个基本环只能断开1条支路，否则会形成孤岛。

2)若多个基本环(至少2个)存在包含的关系，则先断开含分段开关较多的基本环，根据基本环大小依次解环，且公共支路组最多只能断开1条支路。

3)若多个基本环(至少3个)存在两两相交的关系，则公共支路组中至少有1条支路处于闭合状态。

4)若多个基本环(至少3个)同时存在2)、3)这2种情况，N-1个基本环与剩余1个基本环中存在公共支路断开(不包括N个基本环的公共支路集合)，则N个基本环的公共支路集合可存在支路断开。

3 双层优化模型的求解

3.1 改进和声搜索算法

和声搜索算法(harmony searching algorithm,HSA)是一种新的启发式优化算法，由韩国学者Geem等[16]于2001年提出。该算法受到乐师通过反复调整乐器的音调，最终获得美妙和声这一过程的启发而构造的。和声搜索算法具有结构简单、参数少、易于实现等特点，因此广泛应用于各种场景的全局优化中[17-18]。

根据和声搜索算法的寻优过程可知，算法的各个参数设置对寻优性能会产生较大的影响，大多数文献中的参数都采用固定值，都会随着迭代的进行使寻优结果陷入局部最优[19]，因此，本文中将算法参数设置为随着寻优过程的迭代而动态变化。

1)参数改进。在和声记忆库容量(harmony memory size,HMS)确定的前提下，在寻优初期，以较大的和声记忆库选择概率(harmony memory considering rate,HMCR)和较小的音调调节概率(pitch adjusting rate,PAR)选择和声记忆库(harmony memory,HM)中的解向量，确保实现对HM逐步优化的过程和增加解的多样性；寻优后期，HM中解向量之间非常接近，此时需要以较小的HMCR和较大的PAR选择HM中新的解向量，确保在当前解周围进行精细捜索，提高局部捜索的能力,参数改进表达式为

(19)

(20)

式中：HHMCR,max、HHMCR,min分别为和声记忆库选择概率的最大值和最小值；PPAR,max、PPAR,min分别为音调调节概率的最大值和最小值；Fmax为HM中适应度最大值；Fmin为HM中适应度最小值；Favg为整个HM中适应度的平均值。

2)局部最优判断。为了进一步使寻优过程更具有准确性，在参数改进的基础上加入局部最优判断机制，其表达式为

(21)

式中：σ2为解向量适应度方差；HHMS为适应度值的个数；Fi为第i个和声的适应度；Favg为整个和声的适应度的平均值。

σ2反映某一和声的适应度值与期望适应度值之间的偏离程度，σ2越大，说明偏离程度越大，越容易陷入局部最优；反之，则寻优较为合理。

本文中所提算法中参数的设置并不是固定的，而是随着算法的迭代而不断变化，避免了参数设置固定不变的弊端，同时加入了局部最优判断机制，能够较全面地为寻优提供更加有利的条件。

3.2 基于和声搜索算法的模型优化

在现有含DG的配电网重构研究中，大部分文献中都假设给定DG的并网容量和位置，将DG简单地接入配电网，并未考虑配电网重构与DG容量、位置两者之间存在相互制约的关系，因此，在模型求解时，采用双层优化模型来解决两者之间存在的复杂关系。根据上述内容，上层优化模型中以VSI和DG接入系统的网损减小量为目标函数确定DG的位置和容量，下层优化模型中以网损和负荷均衡度为目标函数确定配电网的最优结构。本文中通过上、下两层模型不断迭代，最终得到最优网络结构以及最佳的DG容量和位置，所提出的模型能够更加全面地反映DG优化配置和配电网重构之间相互制约的关系。

本文中所提出的双层优化模型是一个多约束、多目标的优化问题，采用改进和声搜索算法进行优化，双层优化模型中包括最优的网络拓扑结构以及DG安装位置和容量大小。根据2.1节可知，配电网重构的实质是常开的联络开关和常闭的分段开关之间开关状态的交换，因此算法的解向量由2个部分组成，第1部分包括开关状态，第2部分包括DG安装位置和容量大小。文献[20]中对DG并入配电网的数量与产生网损的关系进行了详细的分析，研究表明，当并入DG的数量超过3个时，系统网损减小量增大效果不明显，甚至会减小，因此本文中选择并入DG的数量为3个。由上述内容可知，一组解向量可构造为

(22)

双层优化模型的所有解向量可根据Mi生成，解向量需满足1.1和1.2节中上、下层优化模型的约束条件以及配电网辐射状运行的条件，整个优化模型的解向量为

(23)

3.3 求解流程

双层优化模型的求解流程如图5所示，具体步骤如下：

1)读入原始数据，进行数据预处理，并设置改进和声搜索算法的参数。

3)下层优化模型以步骤2)产生的解向量为初始值，采用改进和声搜素算法对其进行优化求解，确定优化后配电网网络拓扑，更新HM。

4)终止条件的判断。若满足终止条件，即上、下层优化模型产生的解向量均达到最优，则停止迭代，转入步骤5)；若不满足终止条件，则返回步骤2)。

5)输出最优解向量。

4 算例分析

测试系统采用由37条支路组成的IEEE 33节点配电网系统，该系统母线电压为12.66 kV，系统总负荷为3 715 kW+j2 300 kvar，线路与各个节点具体参数取自文献[21]。优化算法采用3.1节所提的改进和声搜索算法，参数设置如下：HHMS=50，HHMCR,max=0.95，HHMCR,min=0.65，PPAR,max=0.7，PPAR,min=0.1，迭代次数取300。

图5 双层优化模型的求解流程

本文中基于配电网重构与DG并网容量和位置存在相互制约的关系提出了双层优化模型，为了证明所提模型的有效性，将优化模型划分为6个场景，具体场景划分如表1所示。

表1 场景划分

为了更加全面地反映负荷的整体性变化，将负荷水平分为以下3种：1)正常，负荷水平系数取1.0；2)轻载，负荷水平系数取0.5；3)重载，负荷水平系数取1.6。由于DG数量的变化会对系统网损产生一定程度的影响，因此本算例选取3个DG接入系统。

根据上述所提出的优化模型和优化算法，对6个场景及3种不同负荷水平的系统分别进行优化，优化结果如表2所示。选取负荷水平系数为1.0的6个场景下的优化结果进行详细分析。在原始状态下，系统未采取任何优化措施，其中系统的有功网损为202.647 1 kW，最低电压在节点18处，且Vmin=0.913 3 p.u.。为了验证本文所提的双层优化模型具有较好的性能，从网损、DG位置、容量和节点电压分布水平3个方面进行详细的对比分析。

从系统有功网损的角度分析，根据表2的优化结果可知，场景2—6这5种不同场景采取不同的优化措施分别对配电网进行优化，系统有功网损依次减小，分别减小到139.743 1、92.200 0、85.400 4、67.940 1、65.446 8 kW，网损减小率逐渐增大，从31.04%增大到67.70%，提升效果较为明显。通过以上结果分析可知，场景6采用的双层优化模型可以使系统网损减小率有较大幅度的提升。

从DG接入位置和容量的角度分析6种场景优化模型的性能，根据表2的优化结果可知，场景1、2未考虑DG的接入，此阶段主要分析场景3—6的优化结果。场景3接入DG的节点位置分别为16、18、31，接入DG的总容量为2.060 1 MW；场景4接入DG的节点位置分别为18、30、32，接入DG的总容量为1.212 0 MW；场景5的优化措施为先DG配置再进行配电网重构，因此DG安装位置、容量与场景3相同；场景6接入DG的节点位置为17、30、31，接入DG的总容量为2.167 2 MW。由分析结果可知，场景6接入DG的容量最大。根据以上分析可以看出，场景6系统的渗透率高达58.34%，属于高渗透率的DG接入配电网，说明该优化模型可以有效地提高DG的并网容量，DG接入的位置相比其他场景更为合理。

本文中仅选取负荷水平系数为1.0的优化结果进行分析。从表2可以看出，负荷水平系数分别为0.5和1.6的2种优化结果与上述分析结果相同。通过从系统网损和DG并网位置、容量2个方面的详细分析，说明本文中提出的双层优化模型即场景6具有较好的性能。

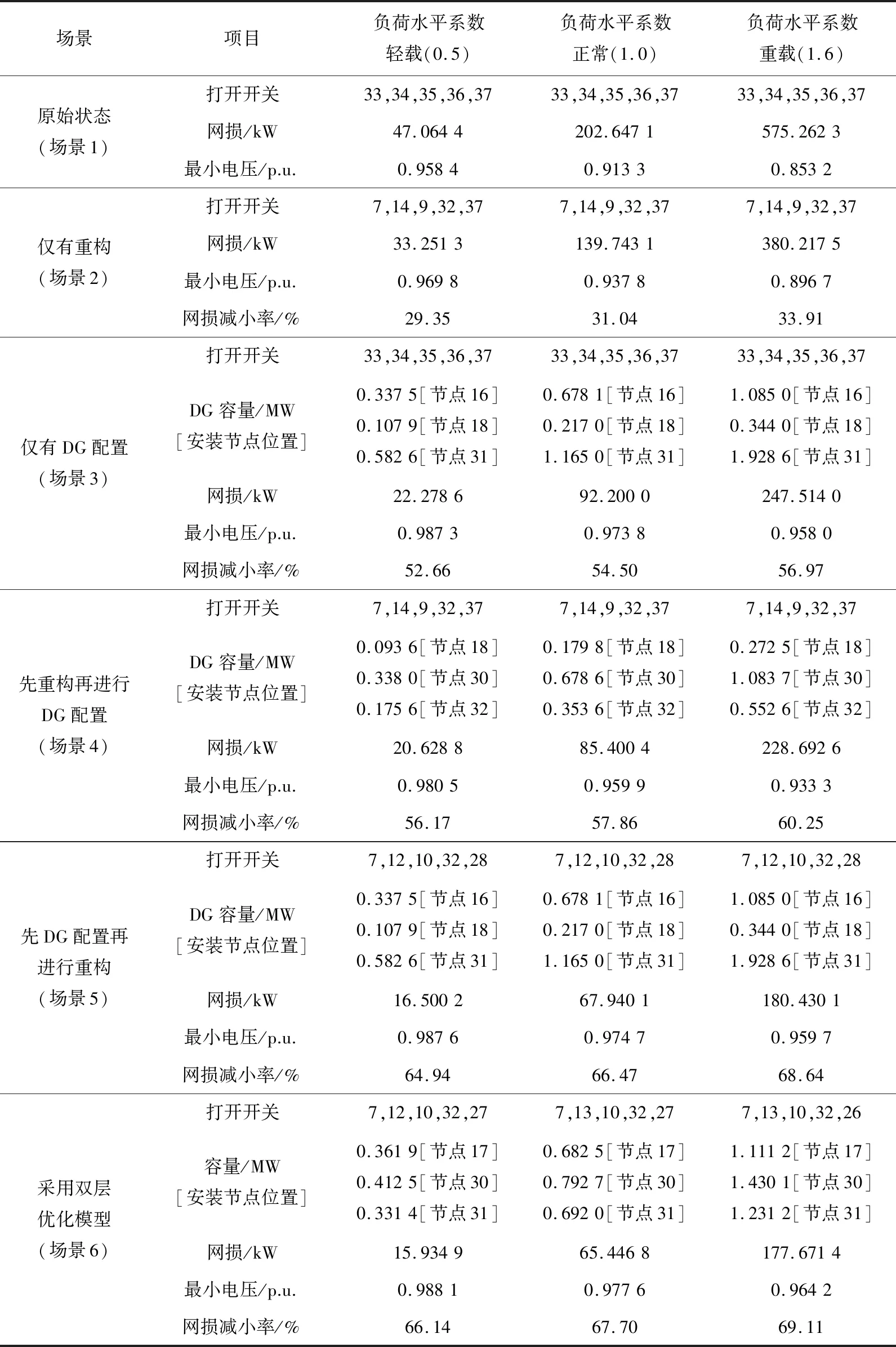
表2 IEEE 33节点配电网系统仿真结果

进一步分析系统节点电压分布，3种不同负荷水平系数下的分布曲线分别如图6所示，其中系统的每一种负荷水平包含6种优化场景，对其进行对比分析。分析图6可知：场景1、2的系统节点电压偏差较大，其原因主要是场景1并未采取任何优化措施。场景2虽然采用重构对配电网进行优化，但只是考虑了单一优化模型。场景3系统节点电压偏差相对较小，其原因主要是该场景虽然也仅采用DG优化配置的单一优化策略对配电网进行优化，但系统的渗透率高达55.45%，DG并网容量较大，导致电压偏差较小。场景4与场景5虽然将重构和DG优化配置均计入优化策略中，但只是将它们之间按照简单的先后顺序进行优化，并未考虑它们之间相互制约的关系。场景4系统的渗透率仅为32.62%，较场景3的低22.83%，DG并网容量较小，因此系统节点电压偏差与场景3相比较大。场景5不仅考虑了重构和DG优化配置，而且系统渗透率为55.45%，因此场景5电压提升效果优于场景3和场景4。场景6采用双层优化模型，考虑了重构与DG位置和容量的关系，其电压分布相比其他5种场景较为平稳，说明了该优化模型能够有效地改善系统中存在节点电压偏差较大的问题。

(a)负荷水平系数为0.5

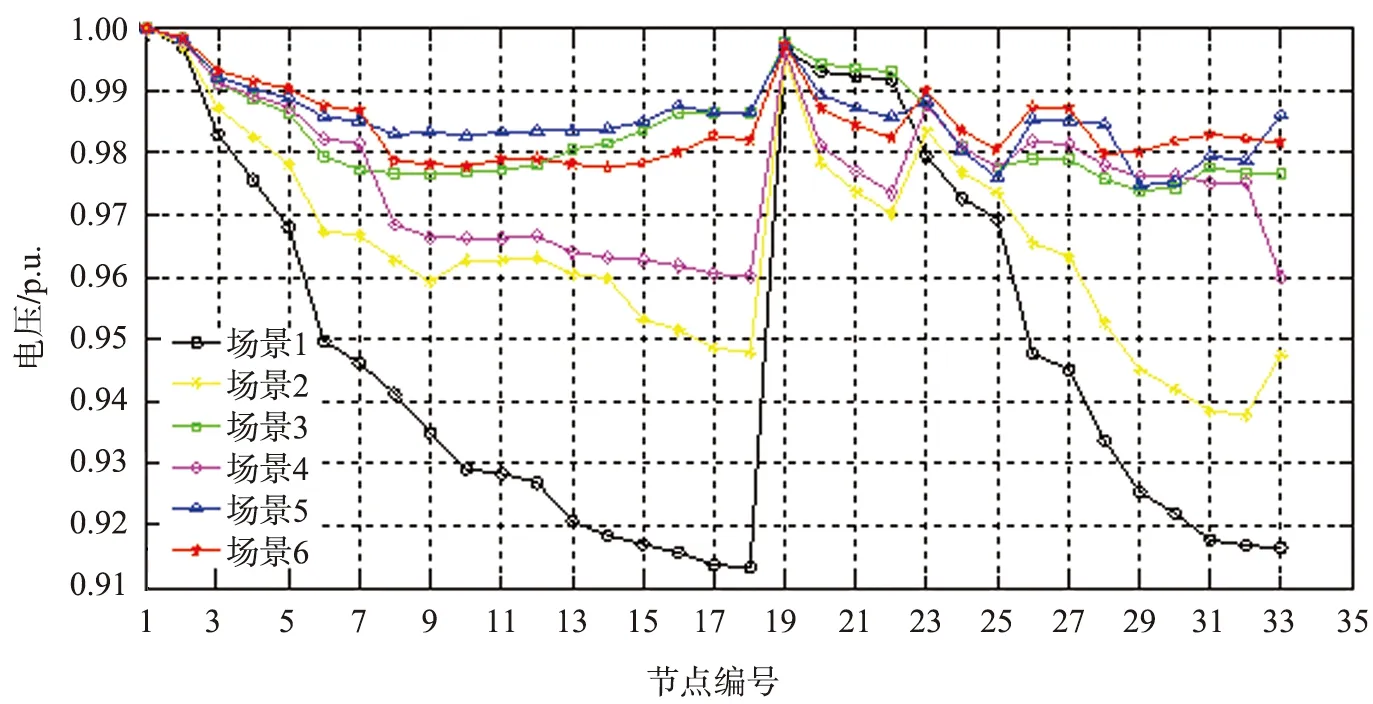
(b)负荷水平系数为1.0

(c)负荷水平系数为1.6图6 IEEE 33节点配电网系统电压分布

为了进一步说明双层优化模型的优越性，将本文中所提方法与文献[14]、[22]的方法进行对比分析，均选取负荷水平系数为1.0的优化场景，对比结果如表3所示。

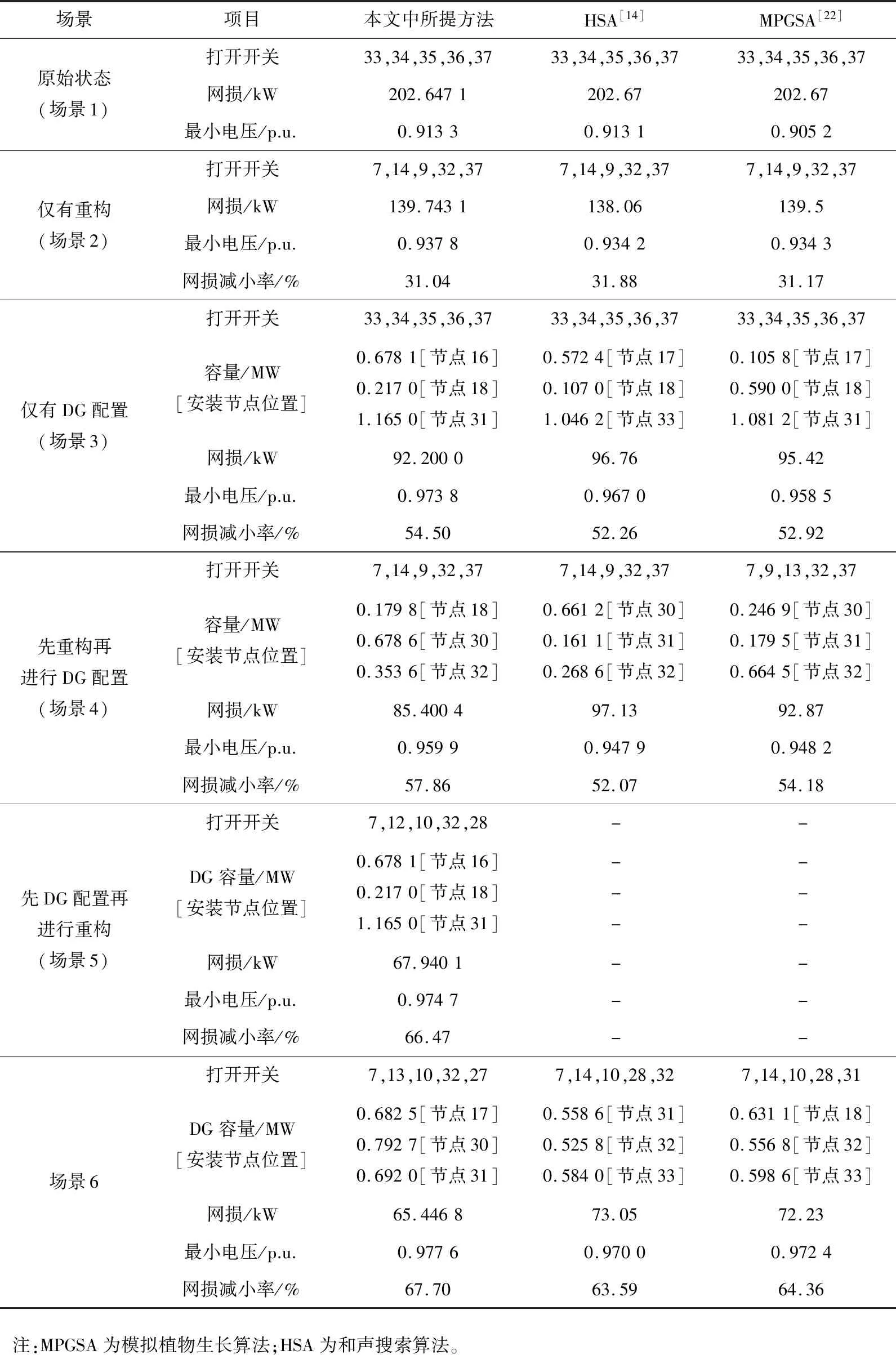
表3 几种配电网重构算法的仿真结果对比

文献[14]、[22]中分别采用模拟植物生长算法(modified plant growth simulation algorithm,MPGSA)和HSA对配电网进行优化，均选取5种优化场景，其中场景5只是简单将DG位置、容量与配电网重构同时考虑，并未将两者相互制约的关系体现出来。为了更加全面地说明各个优化场景对配电网性能的影响，本文中选取6种场景。分析表3的优化结果可知，除场景1以外，本文中采用的5种优化场景与文献[14]、[22]中的相比，在系统网损减小率、节点最小电压、DG并网位置和容量均表现出较好的优化性能，说明本文中提出的优化模型在目标函数的建立和优化策略上更具有合理性，能为配电网重构提供更为准确地参考。

5 结论

在分析现有含DG的配电网重构规划的研究基础上，本文中提出了考虑DG的配电网重构双层优化模型。该方法有效地将DG的位置与容量和配电网重构通过上、下2层优化模型相结合，采用改进的和声搜索算法进行优化，更加全面地体现两者之间的关系。以IEEE 33节点系统为例进行仿真验证，得出以下结论：

1)与已有优化模型相比，本文中提出的优化模型有效地解决了配电网重构过程中将DG位置与容量事先设定的缺陷，使计及DG的配电网重构更加合理。

2)本文中提出的含DG的配电网双层优化模型可有效地提高网损减小率和改善系统安全性，同时可以提升DG的并网能力。

3)本文中所提出的优化模型具有较好的适应性，能够为其他类似优化问题提供借鉴和参考。