基于参数化设计的浮冰区船舶冰阻力研究

童 波，涂勋程，谷家扬，陶延武，张忠宇

（1.中国船舶工业集团公司第七〇八研究所，上海200011；2.江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003；3.江苏科技大学 海洋装备研究院，江苏 镇江 212003）

0 引 言

随着北极航道的初步通航，冰区船舶航行日益增加，但极地区域分布较广的浮冰给船舶安全航行带来一定威胁。浮冰的几何形态及分布规律具有不确定性，船舶航行于浮冰区涉及多体碰撞和流固耦合等相关技术问题，国内外学者在该领域开展了大量研究。

目前，浮冰阻力数值计算和试验研究主要关注浮冰厚度、船冰相对速度、浮冰密集度等因素对船舶冰阻力的影响[1-2]。国内外研究人员发现，基于LS-Dyna软件计算得到的船舶浮冰阻力，仅在较低速度时与试验测试结果比较符合，在高速度点时与实验值结果相差较大[3-4]。冰缘区可分为边缘区、过渡区和内陆区[5]，边缘区到内陆区的浮冰尺度从0.1~100 m不等，具有很强的空间离散性。Jeong等[6]在韩国KRISO海洋工程研究所冰水池中开展了破冰通道宽度和冰块尺度对冰阻力的影响研究。van den Berg等[7]采用数值计算和试验研究相结合的方法，对垂直形状结构与浮冰场的相互作用进行了研究。研究发现，浮冰形状对结构运动方向上的冰荷载平均值和标准差影响较大。Liu[8]提出了一种采用扩张多面体单元离散元模拟浮冰的方法，对北极浮冰区域的某浮式结构进行了冰载荷计算，分析了冰厚、冰浓度、浮冰尺度等冰荷载影响参数，但在计算过程中未使用可破碎的冰体材料，与船冰实际作用情况有所区别。尽管越来越多的学者[9]关注浮冰形状效应和尺度分布规律对冰阻力的影响，但浮冰的生成方法没有通用性，无法满足当前浮冰建模的需求。

本文采用Grasshopper参数设计工具对浮冰区进行了建模，参照真实冰区测量数据，基于遗传算法对浮冰尺度概率分布开展了优化。采用可破碎的各向同性弹性断裂失效模型模拟浮冰，基于LS-Dyna流固耦合方法对船舶在不同浮冰尺度范围的冰区航行进行了数值研究，探讨了浮冰尺度效应对船舶浮冰阻力的影响。

1 浮冰区参数化建模及浮冰尺度概率分布优化

基于Rhino3D平台参数化设计工具Grasshopper生成具有随机分布和非规则形态的浮冰区模型，运用Grasshopper内置的Voronoi运算器生成浮冰二维模型。Voronoi图是关于空间划分的基础数据结构[10]，由一组连接相邻两点直线的垂直平分线所组成的连续多边形。为实现初始冰区尺度、浮冰密集度、浮冰数量等参数控制和初始点集的随机分布，建立相关参数和运算器后，生成“Voronoi-浮冰区”脚本，该脚本共包含五个变量：浮冰区长度、浮冰区宽度、浮冰数量、浮冰位置和Voronoi图缩放因子。由该脚本生成的浮冰密集度为50%、浮冰数量为116块的二维浮冰区模型（200 m×100 m）的可视化参数建模主要流程如图1所示。

图1 Grasshopper可视化参数建模主要流程Fig.1 Visualized parameterized modeling main process of Grasshopper

自然界的浮冰均为非规则多边形，在研究浮冰尺度分布之前，必须选择一个能表征浮冰尺度的特征量，Yulmetov等[11]定义浮冰等效直径（Mean Calliper Diameter，简称MCD）为：MCD=l/π（l为浮冰表面周长，m）。

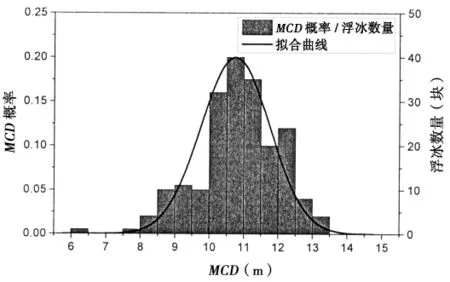
图2浮冰MCD概率分布规律Fig.2 Distribution of probability of brash ice’s MCD

由“Voronoi-浮冰区”脚本生成的浮冰区二维模型是基于随机点分布构成的，随机点的产生属于泊松过程，是一种统计与概率学里常见的离散概率分布类型，因此浮冰MCD概率分布的拟合曲线也符合泊松分布规律，浮冰MCD概率分布直方图及拟合曲线如图2所示。

浮冰模型的建立对于冰阻力预报至关重要。基于Voronoi图生成的浮冰依赖于随机点的生成方式，浮冰MCD概率分布服从泊松分布特性有别于真实浮冰的分布规律。自然环境下浮冰区MCD概率分布基本符合负指数幂函数，为研究不同的浮冰MCD概率分布对船舶冰阻力的影响，本文采用遗传算法对Voronoi图进行了优化（概率分布由正态分布转化为负指数幂函数分布）。通过分析极地浮冰尺度的测量数据，浮冰MCD概率分布的负指数幂函数表达式[11]为：

式中：β为受冰区地理位置影响的参数；Dmin为浮冰最小MCD；Dmax为浮冰最大MCD。

浮冰MCD概率分布优化借助于Grasshopper中的Galapagos运算器，遗传算法是计算数学中常用的搜索算法，采用该算法建立“遗传算法优化-Voronoi-浮冰区”脚本，优化流程主要概括如下：在已知浮冰概率分布函数和浮冰总数的前提下，生成数量确定同时具有一定尺度范围的浮冰，运用遗传算法运算器产生2倍于浮冰数量的“浮点”，将“浮点”累加作用在随机点x、y坐标值上，随机点相对位置的改变影响到各Voronoi图的相对尺度，将基于目标概率分布函数获得的各浮冰面积与优化后的各Voronoi图面积作“差值”计算，当差值之和取最小极限时，则确定为全局最优解。

基于测量数据[11]（Okhotsk海域，2000年2月，Dmin=7 m，β=1.8），对浮冰密集度为50%的目标浮冰区（200 m×100 m）进行优化，优化前后的浮冰区模型如图3所示，浮冰MCD概率分布直方图及拟合曲线如图4所示，可以看出优化后的浮冰MCD概率分布（7 m≤MCD≤20 m）与目标幂函数基本重合，“遗传算法优化-Voronoi-浮冰区”脚本生成的浮冰模型基本符合自然冰区的浮冰分布方式。

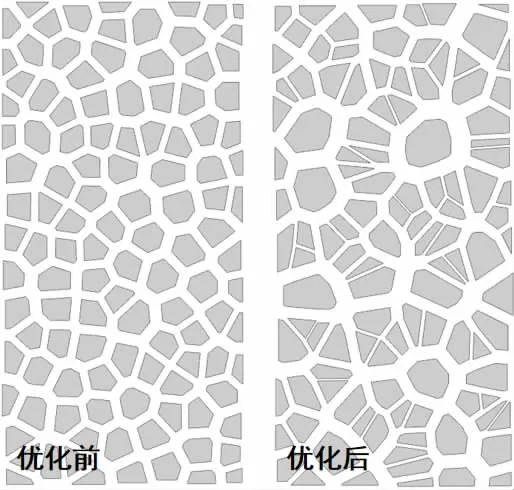
图3浮冰区模型优化前后对比 Fig.3 Comparison of brash ice zone models before and after optimization

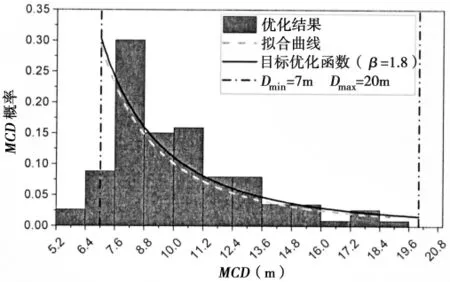
图4浮冰MCD概率分布规律Fig.4 Distribution of probability of brash ice’s MCD

2 浮冰MCD概率分布对浮冰阻力的影响

2.1 数值方法

利用LS-Dyna软件研究“船-浮冰-水”流固耦合问题时，通常采用ALE方法（即Arbitrary Lagrange-Euler）。该方法将Lagrange和Euler方法进行结合，ALE方法突破了固体大变形数值计算的难题，目前已经成为分析大变形问题的重要数值方法。

任意物理量f在ALE描述下对时间的导数由两部分组成：

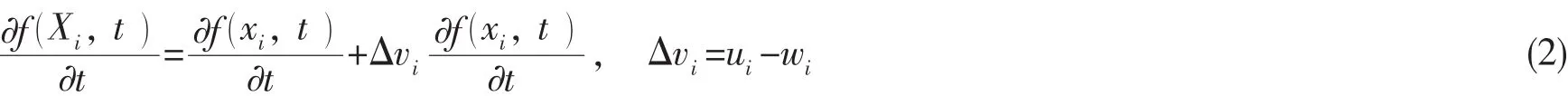
式中：Xi和xi分别为拉格朗日坐标和欧拉坐标，Δvi为相对速度，ui和wi分别为流体质点速度和参考坐标系下的网格速度。通过上式又可导出ALE描述下的流体连续性方程及动量方程，由质量守恒原理用流体密度ρ描述（2）式中的物理量f可得：

（3）式即为流体连续性方程，对于不可压缩流体，可简化为：

结合牛顿第二定律对流体微元运动情况进行分析，可导出流体单元本构方程：

式中：p为流场压强，μ 为粘性系数，τij为应力张量，δij为 Kronecker δ函数。

根据流体单元上压力、质量力、粘性力以及惯性力相平衡的条件可以推出：

将（5）式中的σij代入（6）式中可得ALE描述下的流体动量方程：

LS-Dyna采用罚函数约束的方法来实现流固耦合，程序将自动追踪拉格朗日节点（船体结构和浮冰）和欧拉流体（水和空气）位置间的相对位移，检查每个从节点对主物质表面的贯穿。若发生从节点对主物质表面的贯穿，界面力fs就会分布到欧拉流体的节点上，耦合界面会在ALE的每个输运载荷步中进行重构，对未出现该情况的则不进行任何操作。

界面力大小受贯穿点的相对位置影响，满足如下关系式：

式中：δi为穿透量；ki为接触刚度因子。

2.2 计算模型和参数

计算模型的水域和空气域长宽为280 m×110 m，水深12 m，空气域高度8 m，建模时将二者处理为共面，划分网格时将两种材料处理为共节点，水和空气均采用Null材料模型，状态方程分别采用GRUNISEN和LINEAR_POLYNOMIAL描述，流场外边界全部采用无反射边界条件*BOUNDARY_NON_REFLECTING。流体域实体单元采用变间距网格划分，网格在z方向上以自由液面处为起始面向两端渐变式增大，网格数量为400 400个。

通过Grasshopper“遗传算法优化-Voronoi-浮冰区”脚本得到二维浮冰模型后，建立厚度为1 m的浮冰区有限元模型，浮冰密集度为50%，设置优化前和优化后工况：A1~A5、B1~B5，共计10个工况。优化后工况除浮冰尺度外的其余变量与优化前保持一致，优化工况参照冰区信息如表1所示。

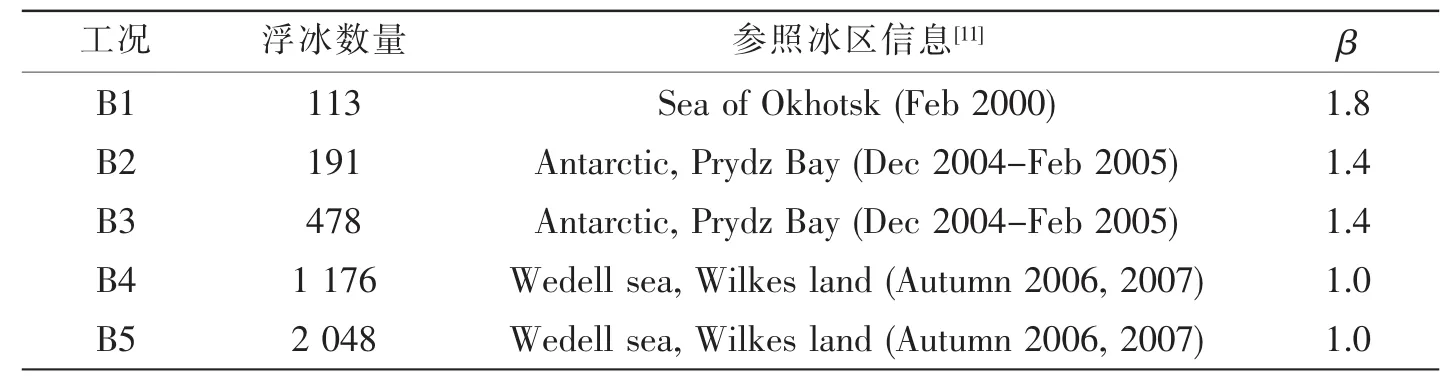
表1优化工况参照冰区信息Tab.1 Referenced ice area information of optimized operating conditions

冰体材料采用*MAT_ISOTROPIC_ELASTIC_FAILURE（MAT_013）。该材料是带有塑性应变失效准则的各向同性弹性断裂失效模型，当有效塑性应变达到失效应变或当压力达到失效截断压力时，单元失去承载应力的能力，偏应力变为零，即材料表现为流体状态，冰材料参数[12]如表2所示。

表2冰体材料参数Tab.2 The material parameters of ice

船舶主尺度如表3所示，船体材料为刚体，约束船体所有节点在z方向上的位移，设定船速16 kns，模拟时间长度为25 s。船体-浮冰接触定义为*CONTACT_ERODING_SURFACE_TO_SURFACE，浮冰自身接触定义为*CONTACT_ERODING_SINGLE_SURFACE；定义流固耦合关键字为*CONTROL_ALE、*CONSTRAINED_LAGRANGE_IN_SOLID。在浮冰区前设置了长75 m的缓冲区以消除波浪对浮冰姿态的影响，浮冰区其余三个方向距离水域边界均为5 m。以A1、B1工况为例，优化前后的船舶-浮冰区有限元模型（空气域已隐去）如图5所示。

表3船舶主尺度Tab.3 Main parameters of ship

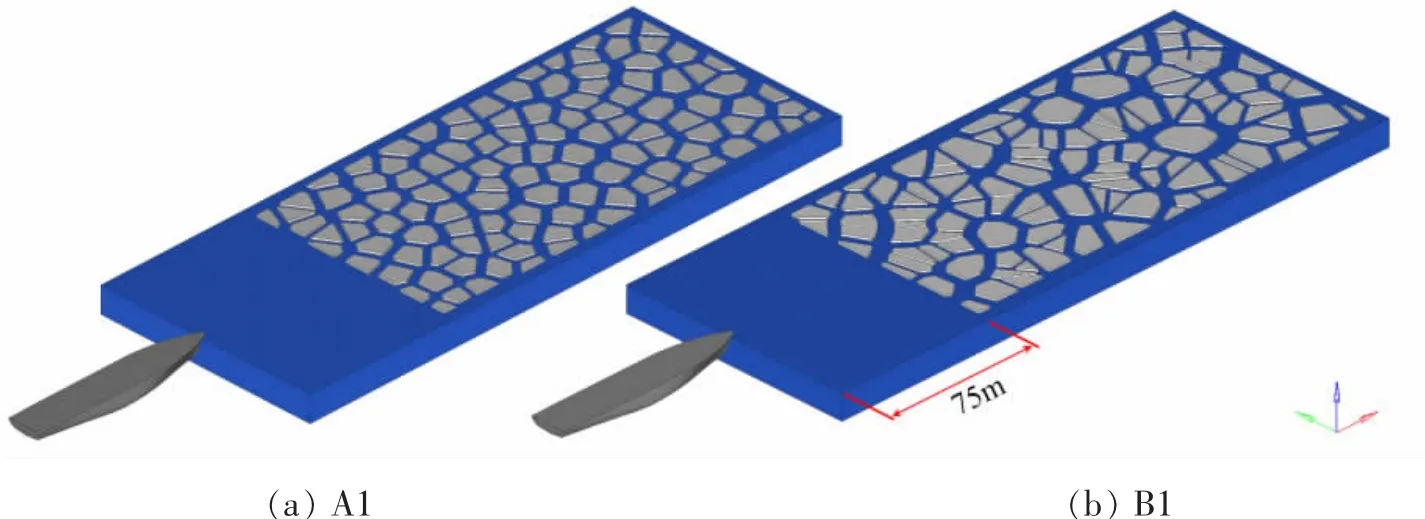
图5船舶-浮冰区有限元模型（隐去空气域）Fig.5 Finite element model of ship-brash ice(Air domain is hidden)

2.3 结果分析

选取优化后浮冰尺度最大的B1工况和浮冰尺度最小的B5工况为例，船舶在浮冰区航行如图6所示。从模拟结果来看，船舶在浮冰区航行时，浮冰均有不同程度破碎，破碎主要发生在船艏附近区域。浮冰在船艏有明显的堆积现象，浮冰发生破碎的同时伴随着翻转，随后贴合船体表面下沉并沿船体滑动，最终到船体艉部被尾流场清除。总体而言，大尺度浮冰的破碎更为剧烈，但翻转和堆积现象相对小尺度浮冰则较弱。

图6数值模拟船舶在浮冰区航行情境Fig.6 Numerical simulation of ship’s navigation in brash ice zone

利用LS-prepost对计算结果进行后处理可得到船舶与浮冰作用的受力，提取x方向分量，即为船舶在浮冰区航行时的浮冰阻力，船舶进入浮冰区后的浮冰阻力-时间历程曲线（10~25 s）如图7所示，分别对比A1~A5和B1~B5工况可以看出，船体受浮冰的冲击频率随浮冰尺度的减小均呈明显增大趋势。

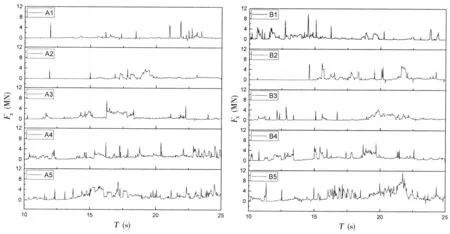
图7浮冰阻力-时间历程曲线Fig.7 Brash ice resistance-time history curve

从图8所示的浮冰MCD范围在各工况下的分布情况来看，B1~B5各工况的MCD分布范围及MCD峰值均大于A1~A5工况，更大尺度的浮冰意味着具有更大的质量，这是优化后各工况的浮冰阻力峰值整体大于优化前的主要原因。

船艏完全进入浮冰区在15 s时刻，对15~25 s内的阻力值进行统计，统计值与MCD平均值关系如图9所示，从图9（a）可以看出各工况的阻力峰值在优化前后的变化，B3工况与上述规律有一定出入，其浮冰阻力峰值相对A3工况更小。原因主要有以下两点：（1）优化浮冰尺度属于全局优化，针对单个浮冰的优化而言仍具有较强随机性，即区域中的某一块浮冰被放大或缩小是随机的，在该工况的船舶航线上可能恰好有较多的浮冰尺度被缩小；（2）因计算资源的限制，模拟船舶在浮冰区航行的时长有限，浮冰运动和姿态变化在一定周期内具有累加效应，B3工况阻力峰值可能并未出现在计算时间内。总体来看，浮冰阻力最大值的影响因素较多，并未随MCD平均值变化呈明显趋势。

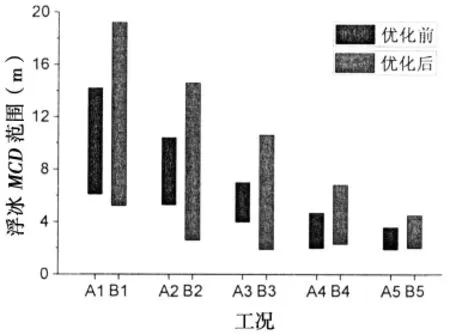
图8浮冰MCD范围分布情况Fig.8 Distribution of brash ice’s MCD range

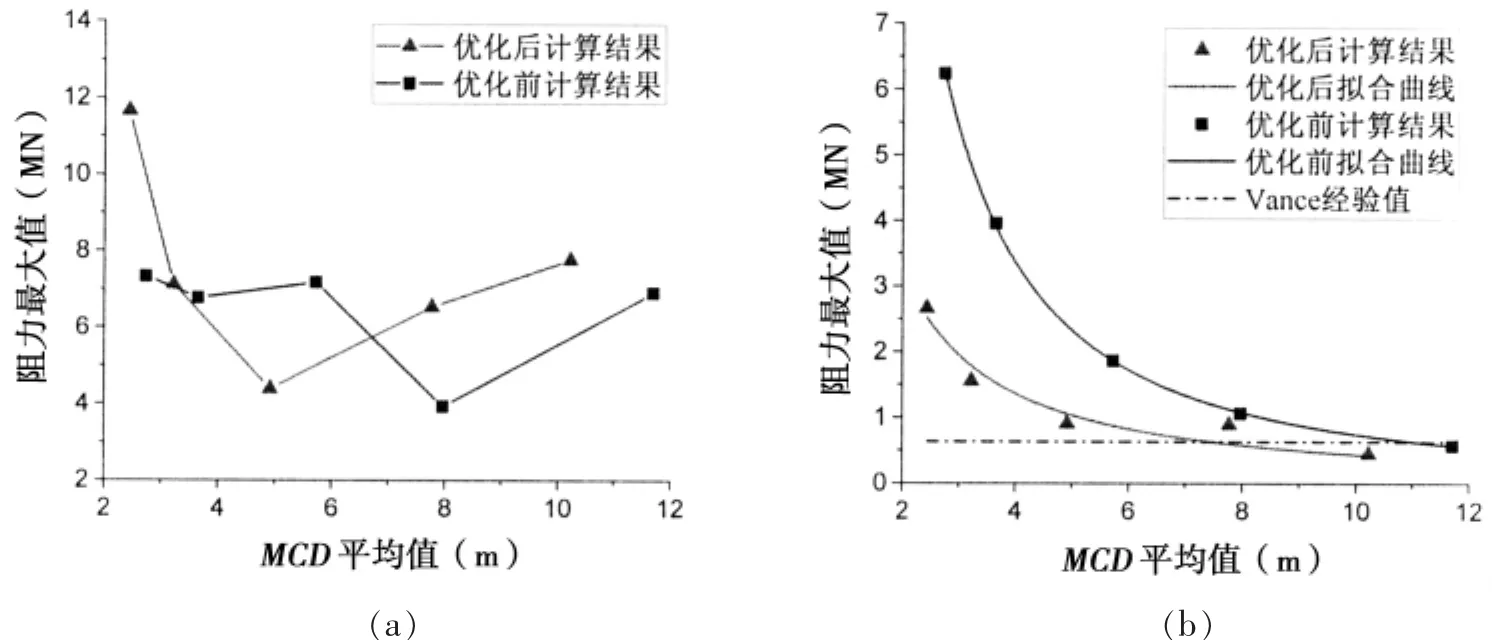
图9浮冰阻力统计值与MCD平均值关系Fig.9 Relationship between statistical value of brash ice resistance and MCD average value

从图9（b）可以看出优化后的浮冰阻力平均值均小于优化前，优化前后的浮冰阻力平均值随MCD增大而呈现负指数幂函数的减小趋势，减小趋势在6 m

将数值模拟结果与Vance浮冰阻力经验公式[13]计算值对比可以发现，当浮冰MCD平均值>5 m左右时，优化后数值结果的浮冰阻力平均值与经验值相差较小。需指出的是，Vance提出的基于全尺度试验得出的经验公式不含有浮冰尺度及浮冰密集度的变量，但该经验值反映出的平均冰阻力在一定程度上也验证了本文数值模拟结果的正确性；另外，浮冰在优化前的模拟结果明显偏高，若不对原本服从正态分布的MCD概率分布向指数分布进行优化，将会得到过于保守的计算结果。

3 结 论

本文采用Voronoi图对不规则几何形态的浮冰进行了参数化设计，并参照真实冰区环境下浮冰MCD概率分布规律，基于遗传算法对其进行优化，以获得接近自然环境条件下的浮冰区模型，将浮冰尺度作为研究变量，采用有限元方法对船舶在优化前后的浮冰区航行开展了数值计算研究，通过数值计算结果结合经验值对比分析得出如下结论：

（1）大尺度浮冰的破碎更为剧烈，但翻转和堆积现象相对小尺度浮冰则较弱，船体受浮冰的冲击频率随浮冰尺度的减小呈明显增大的趋势。

（2）优化后的浮冰阻力峰值整体大于优化前，浮冰阻力峰值受到浮冰形态不规则性及姿态随机性等因素的影响，并未随浮冰MCD增大而呈现出明显趋势。

（3）数值模拟结果在较大MCD范围内与经验值比较符合，浮冰阻力平均值随MCD增大而呈现负指数幂函数的减小趋势，相比大尺度浮冰而言，小尺度浮冰较高频率的冲击载荷对浮冰阻力平均值起到了明显的加强作用。

（4）采用直接基于Voronoi图生成的浮冰区计算的浮冰阻力结果过于保守，对浮冰MCD概率分布进行优化，可以有效降低船舶在小尺度浮冰区受到的平均冰阻力，提高浮冰阻力预报精确性。