考虑残余应力的加筋板结构疲劳裂纹应力强度因子计算方法研究
王艺陶,冯国庆,任慧龙
(1.中国船舶科学研究中心,江苏 无锡 214082;2.哈尔滨工程大学 船舶工程学院,哈尔滨 150010)
0 引 言
加筋板结构是船舶与海洋工程结构最重要、最基本的组成部分,在日常作业和运营过程中海浪的交变载荷作用下,容易产生疲劳缺陷进而导致疲劳破坏。同时,船体结构在焊接过程中,不可避免地存在着相对复杂的焊接残余应力。近年来,关于残余应力对船舶结构裂纹扩展影响的研究受到越来越多的关注[1-4],关于残余应力计算方法的讨论也不断深入[5-7]。研究表明,残余应力场的存在会直接影响到结构的疲劳裂纹扩展,使焊接结构的疲劳裂纹扩展行为呈现出与非残余应力场中扩展不同的特性[8]。因此,研究含有初始裂纹加筋板结构的疲劳裂纹扩展过程的数值计算方法,将有限元数值仿真方法与理论模型相结合,对加筋板结构焊缝周围残余应力分布进行数值仿真,并给出残余应力场中裂纹尖端应力强度因子的计算结果具有十分重要的意义。
本文以有限元数值方法为基础结合Green函数应力强度因子计算理论,建立一套考虑焊接残余应力影响的加筋板结构裂纹扩展的模拟方法。通过对含中心穿透裂纹平板结构、含对接焊缝及中心穿透裂纹平板结构等一系列结构的讨论,给出外部载荷作用下和焊接残余应力作用下有限元数值计算应力强度因子的方法,并验证其有效性;然后,结合裂纹扩展Paris公式,建立一套考虑焊接残余应力影响的裂纹扩展模拟流程,为同类结构裂纹扩展规律研究以及裂纹扩展寿命安全性评估工作提供重要参考和借鉴。
1 含中心裂纹平板结构裂纹应力强度因子计算方法
1.1 应力强度因子计算理论
采用J方法,对应力强度因子进行计算。J积分描述的是由于裂纹的存在所吸收的能量,而应变释放率G描述的则是产生新裂纹面所需要的能量。对于线弹性材料而言,应力强度因子K、路径无关积分J积分和应变能力释放率G可以通过常数联系起来,并且J积分和应变能力释放率是等价的。

式中:ui为位移矢量的分量;ds为积分路径Γ上的微小增量;ω为应变能力因子。
如图1(b)所示,通过散度定理,用裂纹尖端附近一个有限区域来代替积分回路进行J积分的计算。基于这样的思路,(1)式可以转化为:

如图1(a)所示,考虑任意一个围绕裂纹尖端的逆时针回路Γ,数学表达式如下:
针对二维问题可具体展开为:
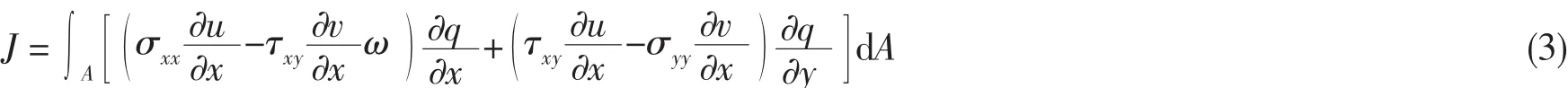
1.2 应力强度因子计算有限元建模方法
含中心穿透裂纹平板结构是研究应力强度因子计算过程中最典型也是最基础的结构之一,由于结构简单且应力强度因子手册已经给出了其应力强度因子的解析解,因此,常常作为应力强度因子计算的首选目标。在研究基于有限元方法计算应力强度因子的过程中,就首先以含中心穿透平板结构为研究对象,建立有限元模型,采用不同尺寸网格对结构进行划分,并采用J积分方法计算裂纹尖端应力强度因子,通过将有限元数值计算结果与理论计算结果的比较,验证有限元数值方法的正确性,并讨论网格大小对应力强度因子计算结果的影响,同时,给出应力强度因子在板厚方向不同位置计算结果的变化情况,最终,确定合适的有限元网格尺寸及计算点位置[9]。
含中心穿透裂纹的平板长l=2 000 mm,宽b=560 mm,厚度t=8 mm,中心裂纹长2a,平板两端受均匀拉应力σ=134 MPa。模型的材料参数E=2.1×105MPa,泊松比μ=0.3。
在进行有限元模型建模时,采用分区域控制网格疏密程度的划分方法,将模型分为三大部分(如图2所示),即接近裂纹尖端及裂纹延长线范围内为区域一,网格密度最大;远离裂纹及其延长线范围为区域三,网格密度最小;中间部分为过渡区域,这种方法可以兼顾裂纹尖端应力强度因子的精度与计算效率。
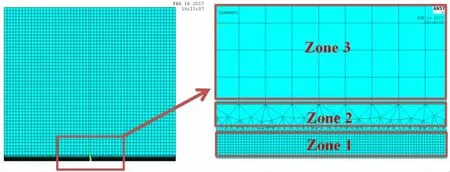
图2有限元模型网格划分区域Fig.2 Zoning of finite element model
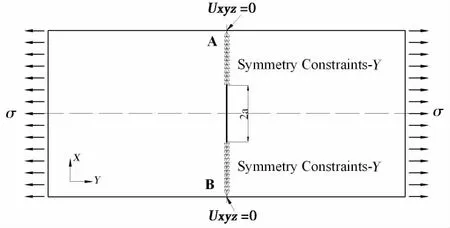
图3有限元模型边界条件及加载Fig.3 Boundary constraint and loading

其中:a为中心裂纹半宽;b为平板宽度;σ为平板两端均布法向拉力。
模型边界条件和加载情况如图3所示。由于模型的对称性,仅对结构的1/2进行建模,在中心裂纹两侧,采用对称边界条件进行约束,平板中心边缘位置处A、B两点采用全约束,模型两端加载均布拉力σ。有限元模型及网格划分情况,如图4所示。
对含中心穿透裂纹的平板结构进行有限元数值计算,如图5所示为有限元模型计算结果的应力云图及裂纹尖端附近Y方向应力结果,这里可以清楚显示出裂纹张开情况及裂纹尖端高应力区的分布范围。
含中心穿透裂纹平板结构裂纹尖端应力强度因子的理论计算式如下式所示:
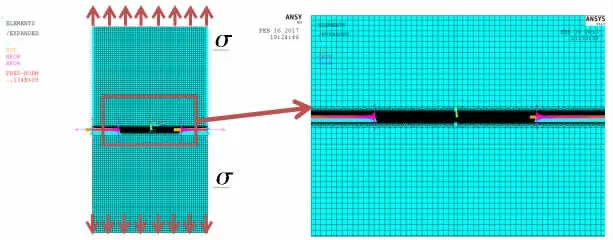
图4有限元模型边界条件及加载 Fig.4 Constraint and loading condition

图5 Y方向应力云图Fig.5 Y component stress contour plot
在计算过程中,裂纹尖端区域细化网格尺寸分别取为10 mm,5 mm,2 mm,1 mm,0.5 mm和0.3 mm,其中选取有代表性的10 mm和0.5 mm的细化模型如图6所示。

图6裂纹区网格细化情况Fig.6 Mesh refinement
裂纹尖端附近网格尺度对应力强度计算精度有一定的影响。于是,将不同网格尺度有限元模型计算结果与理论公式计算结果进行对比,以裂纹长度为a=50 mm,σ=134 MPa的计算结果为例,如表1所示。由结果可知,有限元模型计算结果与理论公式计算结果基本一致,证明有限元数值计算结果是正确有效的。

表1应力强度因子有限元结果与理论结果对比Tab.1 Comparison of finite element results and theoretical results
同时,随着网格密度增加,网格尺度的逐渐减小,应力强度因子的有限元模型计算结果逐渐增加,与理论公式计算结果间的误差逐渐减小,当网格尺寸为1 mm时,误差仅为-0.31%,但当网格尺度继续减小,误差又逐渐升高。可见,有限元网格的尺度并不是越小越好,权衡计算精度与计算效率的关系,选取裂纹尖端附近网格尺度为0.5 mm或1 mm进行计算,应力强度因子计算结果均是相对准确的。两种网格尺寸下应力强度因子计算结果与理论值对比情况如图7所示。
另外,由于平面应力/平面应变效应的不同,同一裂纹长度下应力强度因子在厚度方向存在一定的变化,如图8所示,本文所涉及的应力强度因子均取板厚中心处最大值。

图7不同网格尺寸计算结果对比Fig.7 SIF in different mesh refinement
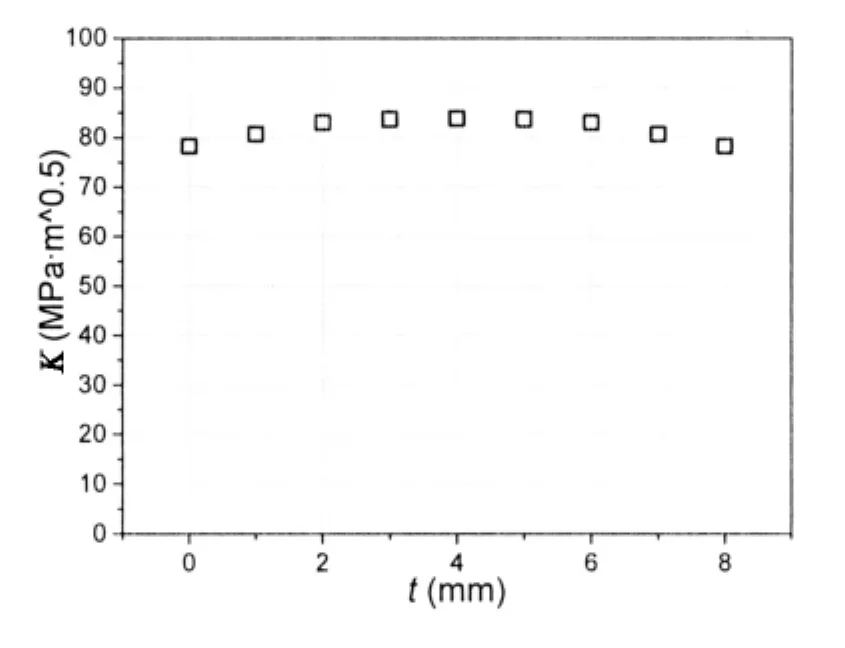
图8应力强度因子厚度方向变化Fig.8 SIF in different thickness
2 焊接残余应力下应力强度因子的模拟方法
2.1 焊接残余应力对裂纹扩展的影响
在计算焊接残余应力分布下应力强度因子时,需要首先确定结构中焊接残余应力的分布。本文选取Faulkner模型对焊接残余应力分布进行模拟,具体分布形式如图9所示,其中最大残余拉应力值σRESmax取为材料的屈服极限,残余拉应力区域范围占板宽度的η倍,即焊接残余拉应力宽度为η×tplate,这里η通常取为3.5或4,而焊接残余压应力的大小及范围则由平衡条件得到。Dexter在相关研究中已经验证[10-11],采用Faulkner残余应力分布模型模拟船舶加筋板结构焊接残余应力形式合理可行。

图9 Faulkner残余应力分布模型Fig.9 Faulkner’s residual stresses model

图10裂纹区网格细化情况Fig.10 Mesh refinement
在计算残余应力分布下应力强度因子的理论模型可基于Green函数建立,应力强度因子KRES的计算公式表示为:

计算原理的示意图如图10所示。由图中可见,一对单独作用在裂纹面上载荷F被转化为作用在微元dx上的分布应力σ。
尽管焊接残余应力分布中既存在残余拉应力又存在残余压应力,但对裂纹扩展速率产生影响的部分仅是高压应力区域这部分应力,也就是说,焊接残余应力只会抑制疲劳裂纹的扩展,而不会使裂纹扩展速率增加。这是因为疲劳裂纹扩展的驱动力是应力强度因子范围ΔK,而真正对裂纹扩展起作用的是有效应力强度因子ΔKeff,即只有使裂纹张开的那部分应力强度因子才对裂纹扩展起作用。因此,当应力比R≥0时,在考虑残余应力引起的应力强度因子KRES与外部其他载荷引起的应力强度因子Kapp进行叠加的情况下,焊接残余应力对裂纹扩展影响关系的判定关系可表示为:

2.2 焊接残余应力下应力强度因子的计算
取含中心穿透裂纹及对接焊缝的平板结构,其中长度L=2 m、宽度W=1 m、厚度B=8 mm,计算其在焊接残余应力区内一系列裂纹长度下的应力强度因子值,其中,中心穿透裂纹长度取为a=0.01~0.2 m。由Faulkner残余应力分布模型可知对接焊缝两侧残余应力的分布,如图11所示为平板结构尺度及其残余应力分布情况。
采用梯度温度法模拟焊接残余应力分布时,需要在不含裂纹的完整结构模型上施加温度梯度,使结构在温度应力作用下收缩或膨胀,从而产生相应的残余应力分布。具体方法是:以焊缝所在位置为中心,以等间距向两侧施加3到5个温度应力梯度,范围总宽度根据Faulkner模型控制在η×tplate(这里η取3.5)范围内。计算过程中通过多次尝试反复迭代,选择适合的温度载荷值使其满足Faulkner模型的残余应力分布形式。对于含中心穿透裂纹及对接焊缝平板结构,这里模拟的残余应力分布为焊缝中心处最大残余拉应力取材料屈服极限350 MPa,分布情况如图12所示。
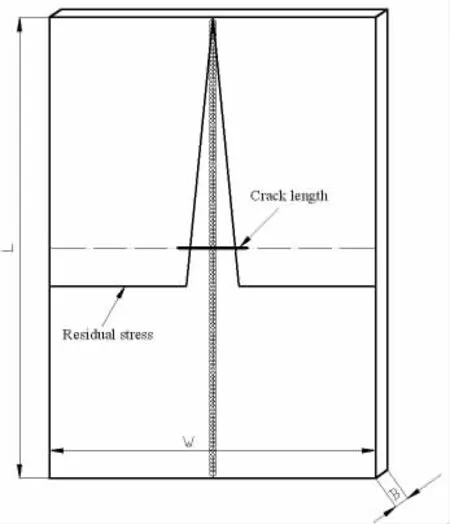
图11含中心穿透裂纹及对接焊缝平板结构Fig.11 Center cracked plate with butt weld
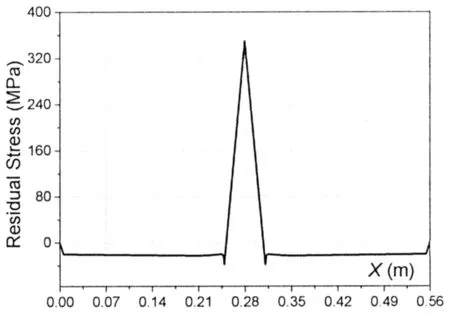
图12残余应力分布Fig.12 Residual stress distribution
由于平板结构的对称性,这里仅对平板结构的1/2部分进行有限元建模。在确定模拟残余应力的温度梯度后,在有限元模型中引入中心穿透裂纹,具体方法是将裂纹面处相应位置的节点进行边界释放,从而形成中心穿透裂纹。在有限元分析过程中,为保持整体结构的应力平衡,原始的残余应力将进行重新分布以达到新的平衡。
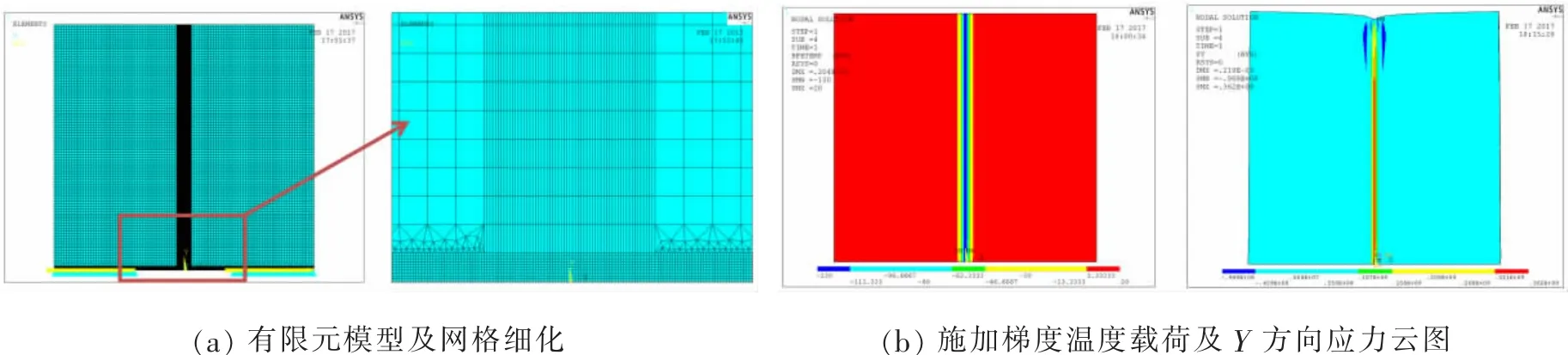
图13裂纹区网格细化情况及温度梯度Fig.13 Mesh refinement and temperature loads
有限元模型网格划分、边界条件、温度梯度及相应的应力云图如图13所示。取一系列裂纹长度计算残余应力分布下的应力强度因子,并与理论近似计算值进行对比,结果如图14所示。由图中结果可知,有限元数值模拟计算结果(图中FEM)与理论近似计算值(图中Analysis)吻合良好。可见,以有限元数值模拟方法为基础,采用梯度温度载荷模拟残余应力分布,对应力强度因子进行计算的结果是准确有效的。
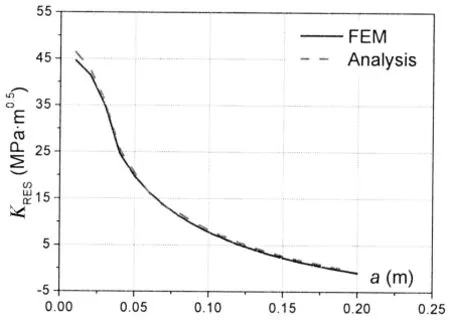
图14有限元模型与理论模型KRES计算结果对比Fig.14 Comparison of KRESfrom FEM and analysis
3 含中心穿透裂纹加筋板裂纹应力强度因子计算方法
在验证了有限元方法模拟焊接残余应力分布及应力强度因子计算在含中心穿透裂纹及对接焊缝的平板结构中的有效性后,将其进一步推广到加筋板结构,并将计算结果与已知文献计算结果进行对比,证明其在含中心穿透裂纹加筋板结构中计算的可靠性。
选取与文献[10] 尺度相同的船体结构中典型的加筋板结构,详细尺寸见图15所示。加筋板中残余应力的分布情况如图16所示,这里是加筋板结构中残余应力测试结果与Faulkner模型模拟结果的对比情况,可见Faulkner模型对残余应力的模拟基本可以反映残余应力的真实分布。因此,在计算过程中仍然采用Faulkner模型残余应力分布对有限元模型进行加载。
为模拟加筋板中的残余应力分布,采用梯度温度法,在焊缝两侧3.5tplate宽度内施加一系列温度载荷,计算过程中经过多次尝试反复迭代,确定温度梯度,使其满足Faulkner模型的残余应力分布形式。由于加筋板结构的对称性,仅对1/4部分的加筋板结构进行有限元建模,边界条件设置及有限元模型如图17-18所示。
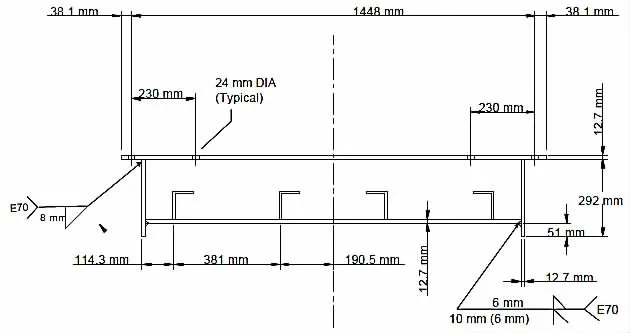
图15加筋板结构示意图Fig.15 Stiffened panel sketch
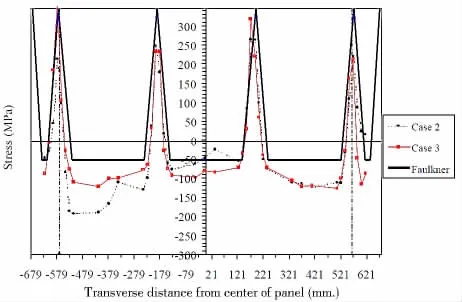
图16 Faulkner残余应力模型与试验值比较Fig.16 Faulkner residual stress vs tests
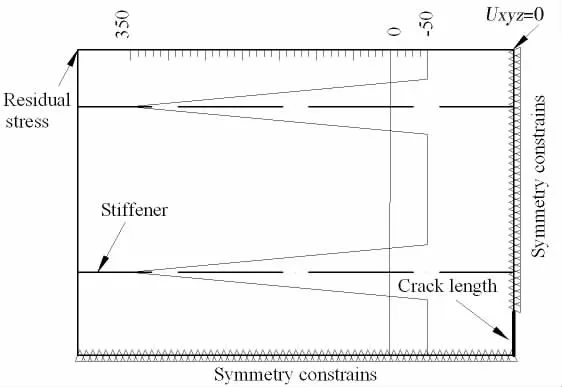
图17有限元模型边界条件及加载情况Fig.17 Boundary constrains and loading

图18加筋板有限元模型Fig.18 Finite element model of stiffened panel
取一系列裂纹长度,计算残余应力分布影响下的应力强度因子,并与理论近似计算值和文献计算结果进行对比,结果如图19所示。可见,理论近似计算值(图中Analysis)与文献计算结果(图中Reference)吻合情况较好,而有限元数值模拟计算结果(图中FEM)仅在焊缝附近与其他两种计算方法存在一定差距,其余位置吻合情况较好。由于邻近焊缝周围,焊接残余应力表现为拉应力,而拉伸残余应力对裂纹扩展速率没有影响,所以这里的差异并不会影响最终计算结果。因此,以有限元数值模拟方法为基础,采用梯度温度载荷模拟残余应力分布,并对应力强度因子进行计算的方法是可行且可靠的。

图19 KRES计算结果对比Fig.19 Comparison of KRES
4 考虑残余应力的裂纹扩展数值模拟流程
应力强度因子计算是裂纹扩展模拟的关键环节。得到了符合载荷特性与结构特征的应力强度因子计算值,便可进一步开展考虑残余应力裂纹扩展的数值模拟工作。
根据Paris公式的定义,疲劳裂纹扩展速率如下式所示:

其中:N为载荷循环的次数;C和m为疲劳裂纹扩展材料参数。将Paris公式整理并转化为积分形式:


在对裂纹扩展过程进行模拟过程中,首先给定初始裂纹长度a0,根据有限元数值计算结果可得到对应的应力强度因子范围ΔK0,选择合适的载荷循环次数ΔN,则可根据(9)式计算得到这一时刻的裂纹长度增量Δa0,将初始裂纹长度a0与裂纹长度增量Δa求和,如(10)式所示,则可得到新一时刻的初始裂纹尺寸ai。

以此类推,经过逐步迭代计算,则可获得相应载荷循环次数所对应的裂纹长度。这里可将整个裂纹扩展计算过程采用APDL参数化设计语言进行编程处理,形成计算模块嵌入有限元计算软件中。裂纹扩展数值计算模块主要分析流程如图20所示。
于是,裂纹长度增量Δa则可表示为:

图20模块计算分析流程图Fig.20 Flow chart of APDL module analysis process
5 数值计算方法的试验验证
5.1 加筋板裂纹扩展试验概况
加筋板长1 000 mm,带板宽560 mm,带板中心位置为加强筋结构,加强筋面板宽90 mm,厚8 mm,腹板高136 mm,厚6 mm,加筋板两端圆孔为装夹用螺栓孔。加筋板模型中间部分,加强筋与带板相交处,采用线切割方法分别在加筋板腹板和带板上加工长度相同的预制裂纹,位置及尺寸如图21所示。
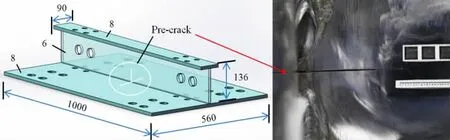
图21加筋板试样几何尺寸及预制裂纹Fig.21 Detailed geometry of specimen and wire-electrode cutting pre-cracks

表2试样加载信息Tab.2 Test specimen matrix
试验采用单侧轴向加载,应力比为0.1,载荷形式为正弦循环载荷,共进行5组试验,各组试验的加载信息如表2所示。试验过程中,每隔相等时间间隔记录裂纹长度,试样端部疲劳裂纹远场应力监测持续试验整个过程。图22所示为试样安装就位后的情况。
5.2 试验结果和数值计算结果的比较
将拉伸载荷作用下,加筋板带板裂纹扩展有限元数值计算结果与试验结果对比,结果如图23所示。由残余应力作用下应力强度因子的计算结果可知,拉伸载荷作用下加筋板带板上残余应力压应力值较小,对裂纹扩展速率影响不大,因而在裂纹扩展过程模拟中是否计及残余应力对计算结果影响不大,总体上计算结果与试验结果吻合情况良好。

图22加筋板试样安装就位Fig.22 Specimen in place


图23带板裂纹数值计算结果与试验结果对比Fig.23 Comparison of simulation results and test results for plate
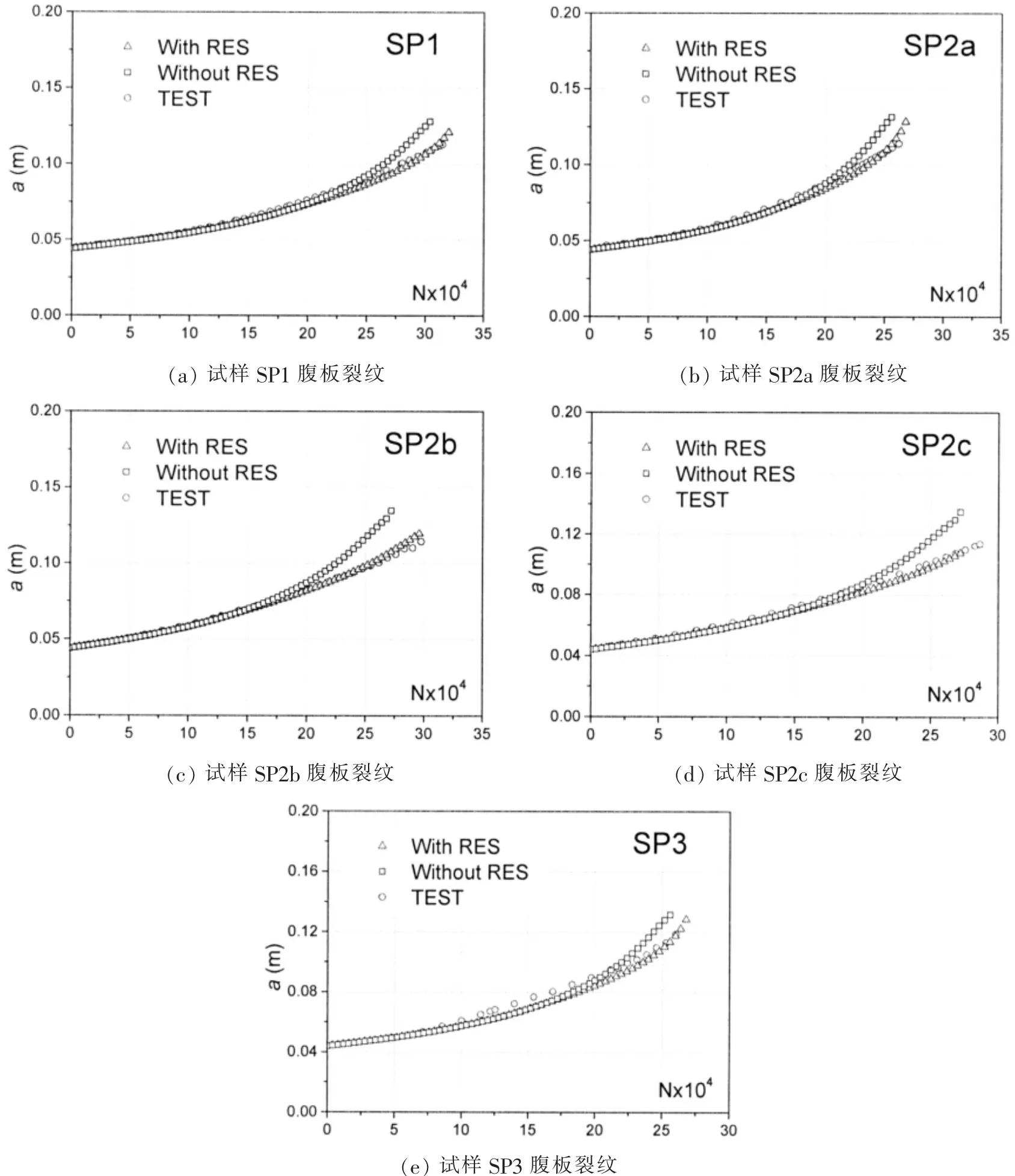
图24腹板裂纹数值计算结果与试验结果对比Fig.24 Comparison of simulation results and test results for web
加筋板腹板裂纹扩展有限元数值计算结果与试验结果对比情况如图24所示。由残余应力作用下应力强度因子的计算结果可知,加筋板腹板残余压应力较大,且由于残余应力对裂纹扩展速率的影响是一个累积的效果,因而在裂纹扩展的中后期,残余压应力的效果开始显现,从结果上看,计及残余应力的计算结果与不考虑残余应力的结果开始产生差距,且计及残余应力的计算结果明显更加符合试验中的实测结果。同时可知,本研究中加筋板腹板裂纹受残余应力影响较大,且对裂纹扩展有一定的抑制作用。
6 结 论
本文开展了焊接残余应力影响下加筋板结构裂纹应力强度因子计算方法研究,分析了焊接残余应力对裂纹扩展的影响,给出了常规外载荷以及残余应力下应力强度因子的数值模拟方法,建立了考虑残余应力的裂纹扩展数值模拟流程,并对数值计算方法进行了试验验证,为后续含复杂组合裂纹加筋板结构裂纹扩展模拟奠定基础。通过本文研究,可得如下结论:
(1)通过对不同网格划分规则下,含中心裂纹平板结构应力强度因子理论计算值与有限元数值模拟值的比较结果可知,网格尺度为1 mm时,计算精度最好,与理论值误差可控制在0.5%以下;
(2)给出了焊接残余应力对裂纹扩展影响的判断关系表达式。分析结果表明,焊接残余应力不会加速裂纹扩展速率,但是在特定条件下会对裂纹扩展速率起到抑制作用;
(3)提出了基于温度梯度法模拟焊接残余应力的有限元方法,分别对含中心裂纹平板、含初始裂纹的加筋板结构残余应力下应力强度因子进行了计算,计算结果与理论值和试验值吻合情况良好。

