斜面上定向抛体运动的初速度放大镜效应

王 磊 陈建文

(1. 盘锦市高级中学,辽宁 盘锦 124000; 2. 盘锦市辽东湾实验高级中学,辽宁 盘锦 124000)

1 斜面抛体运动击中斜面速度的决定因素

平抛运动是高中物理曲线运动部分的一个典型问题．处理该类问题常用方法是速度分解法．将平抛物体的运动分解为水平方向和竖直方向．如果让物体抛出时的速度与水平方向成一个角度，则平抛问题变为斜抛问题,处理方法与斜抛类似，也采用正交分解的方法．如果斜抛的出发点和着落点都在某一斜面上,则可以将速度沿斜面方向和垂直斜面方向分解来简化处理问题．请看这样一个物理竞赛问题.

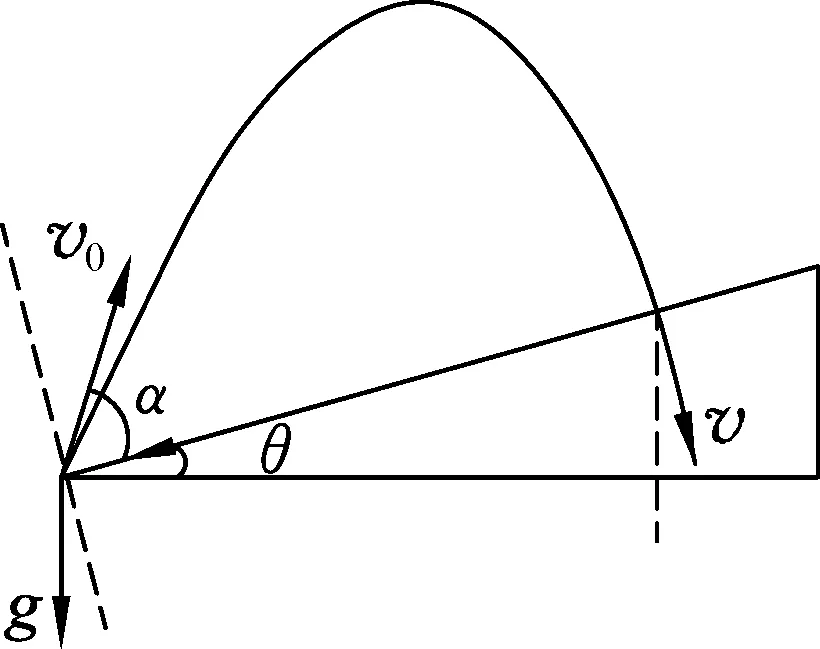
图1

问题1:从倾角为θ的斜面底端以初速度v0抛出一个小球,小球与斜面发生完全弹性碰撞后从原路返回抛出点．试求抛出时的速度．

小球碰撞后原路返回,说明小球与斜面正碰,即小球与斜面相撞时的速度v垂直于斜面(图1).

末速度v垂直于斜面方向:

(1)

小球位移沿斜面方向:

(2)

由(1)、(2)两式可得

cotα=2tanθ.

(3)

图2

由此可得,只要小球抛出方向与斜面成角α,满足cotα=2tanθ,小球就会垂直落向斜面,并原路弹回．即小球是否能垂直落向斜面,与小球的速度大小无关,只与小球的抛出角度有关,只要满足小球抛出方向与斜面成角α,不同速度对应的所有轨迹均与斜面垂直．而增大小球的初速度相当于放大了抛体轨迹的图像(图2),那么只有末速度与斜面垂直情况下才与初速度大小无关么?

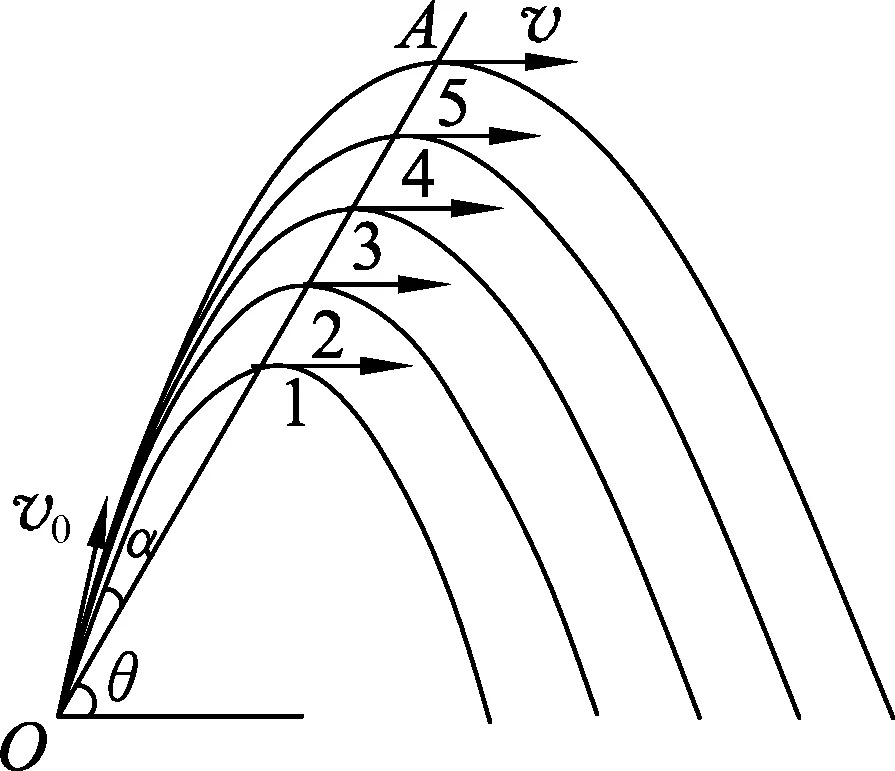
图3

猜想:小球以任意一个角度的末速度落向斜面也只与初速度角度α有关,而与初速度大小无关．

为验证上述猜想,先考虑特殊的角度,如小球水平落向斜面(图3)．小球末速度竖直方向分量为0:

v0sin(α+θ)-gt=0.

(4)

小球位移沿斜面方向(2)式仍然成立，由(2)式可得

gcosθt=2v0sinα.

联立(4)式可得[1]

v0sin(α+θ)cosθ=2v0sinα.

进一步整理有

sinαcos2θ+cosαsinθcosθ=2sinα.

两边同时除cosα有

tanαcos2θ+cosθsinθ=2tanα.

进一步整理有

cosθsinθ=tanα(2sin2θ+cos2θ).

两边除cos2θ有

tanθ=tanα(2tan2θ+1),

整理得

(5)

由此可得在斜面上抛出小球,使小球水平击打到斜面上,只需使小球与斜面成满足(5)式成立的α角,与小球初速度v0大小无关,猜想成立．

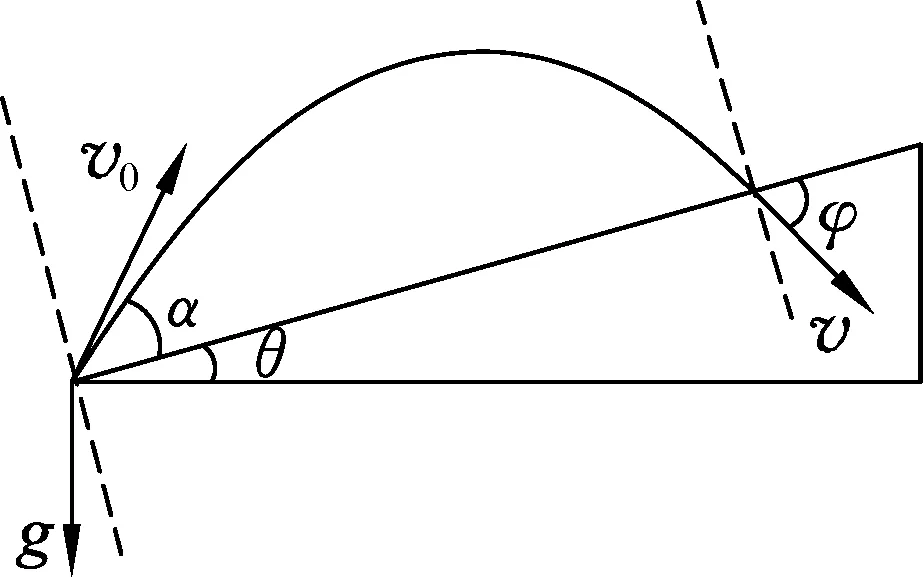
图4

为严格证明该猜想成立,假设小球末速度与斜面成任意角度φ(图4),求证该假设成立前提下对初速度v0的要求与v0大小无关只与v0方向有关．

小球末速度v与斜面成角φ有

(6)

小球位移沿斜面方向(2)式仍然成立得

代入(6)式整理得

等式左侧分子分母同除v0cosα并整理得

(7)

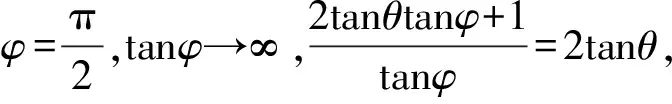
2 定向斜面抛体运动轨迹与初速度大小的关系

图5

问题2:当小球抛出速度与斜面成角α则不论初速度v0多大,小球都以相同的角度击中斜面,那么小球在此过程中,沿斜面位移l和小球运动过程中离斜面最远距离h(图5)分别与初速度v0又有怎样的关系呢?

由(2)式可得gcosθt=2v0sinα,即小球落回斜面所用时间

(8)

小球沿斜面方向做匀减速直线运动有

带入(8)式可得[2]

进一步整理得

(9)

由(9)式可得小球沿斜面位移l与小球初速度v02成正比．

小球离斜面距离最大时,垂直于斜面的分速度为0,此时运动时间为

(10)

垂直斜面方向,小球做匀减速直线运动

代入(10)式得

(11)

由(11)式可得小球运动过程中距斜面最远距离h也与小球初速度v02成正比．

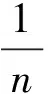
3 定向斜面抛体运动轨迹与斜面所围面积与初速度大小的关系

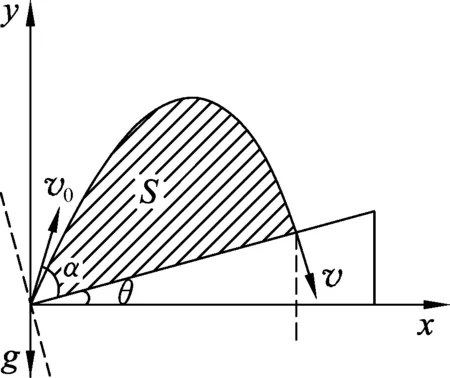
图6

问题3:小球沿斜面的位移l、小球轨迹离斜面最大距离h都与v0的平方成正比,而l与h均是小球抛物轨迹与斜面围成的面积S的线性尺度(图6)．那么面积S与v0有怎样的关系呢?

以抛出点为坐标原点,水平方向为x轴,竖直方向为y轴建立坐标系,抛物线方程[3]为

(12)

斜面方程:

y2=tanθx.

(13)

抛物线与斜面围成的面积

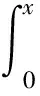
(14)

将(12)、(13)式代入(14)式得

(15)

小球与斜面击中点水平坐标

(16)

将(16)式代入(15)式的积分上限得抛物线与斜面围成的面积

整理得

6cos(α+θ)sinθ-4sinα].

进一步整理得

(17)

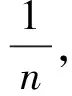
4 总结

通过对斜面抛体运动的计算研究得到以下结论:

(1) 斜面抛体运动的物体击中斜面的速度方向仅由初速度方向决定,与初速度大小无关,把物体以恒定的方向做斜面抛体的运动可称为定向斜面抛体运动;

(2) 定向斜面抛体运动物体击中斜面的速度大小与初速度成正比;

(3) 定向斜面抛体运动物体沿斜面位移、运动轨迹离斜面最远距离与速度平方成正比;

(4) 定向斜面抛体运动物体运动轨迹与斜面围成面积与初速度的4次方成正比．

通过以上的结论进一步得出定向斜面抛体运动轨迹的动态模型:定向抛体运动轨迹图像随着初速度v0大小的变化而变化,相同v0方向不同v0大小的所有定向抛体运动轨迹图像是相似的,初速度v0起到定向斜面抛体运动轨迹图像缩放的决定因素．当初速度v0变成nv0时,整个抛体轨迹图像像在n2倍的放大镜观察下一样扩大成原来的n2倍,末速度v变成原来的n倍,抛体轨迹与斜面所围图像面积扩大为原来的n4倍．所以这个结论不妨称之为定向斜面抛体运动的初速度放大镜效应．