基于OpenCV 的二维渐变图像数据还原
郭佳
(国家超级计算天津中心,天津300457)
0 引言
在石油、勘探、气象等行业中,常常要将采集数据或计算结果以二维图像的方式直观地展示在电子或纸质材料中,渐变图就是其中一种常见的成图方式,而当科研人员在原始数据缺失的情况下,如何从渐变图中还原出原始数据,以便于做进一步的科研用途,这对于数据还原或降低数据重新获取成本方面都具有重要意义。
本文采用图像处理库OpenCV[1]结合二维差值算法设计并实现出从渐变图还原数据的基本流程,不仅能有效还原出原始数据,对于因为标注等原因造成的缺失数据图像也能有很好的还原效果。
1 算法流程
将数据生成渐变图的一般过程是:选择一种数值到颜色的映射表,然后遍历二维数据中的每个标量值,计算该值对应的映射颜色,于是二维数据转化成了二维图像,如图1。
而从图像还原数据的过程可以看成图的逆过程,它的过程如下:
(1)矩形检测:识别图像中的渐变图主区域,以及颜色棒区域;
(2)建立映射表:根据颜色映射区域,建立颜色到数值的映射表;
(3)离散点识别:遍历渐变图,将各像素点颜色值识别成其标量值;
(4)数据网格化:将识别出的散点值网格化为二维数据。

图1 数据成图的一般过程
1.1 矩形检测
矩形检测的目的是识别出图像中的颜色棒区域和渐变图区域。矩形检测和识别是机器视觉领域中的重要内容,人们已经研究出了很多矩形检测算法,如C.Rosito Jung 和R. Schramm 提出的一种基于窗口化的Hough 变换的矩形检测方法[2],张从鹏等人提出的基于Harris 角点的矩形检测算法[3]。
在大部分矩形检测算法中,首先要检测出组成矩形的4 条直线,再计算这些直线的4 个交点作为矩形的角点位置,于是矩形检测问题就转化为直线检测问题,在直线检测中应用最广的当属霍夫直线变换算法,但是该算法会容易检测出多余的直线,结果冗余信息较多,尤其是颜色棒区域的边长很短,非常容易受到干扰,所以本文通过像素搜索方法去寻找矩形4 个边界的位置。
在OpenCV 中进行寻找渐变图矩形和颜色棒矩形边界的实现过程为:
(1)通过cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)函数将原始彩色图像转换为单通道灰度图,其中img为原始输入的彩色图像;
(2)通过cv2.threshold(gray,thresh,maxval,type)对灰度图进行二值化处理,将图像区分为空白和非空白部分,其中gray 为上一步骤输出的灰度图;
(3)从整个图像的中间列开始向右搜索,可以找到渐变图区域与颜色棒之间的白色部分,以此为界限将图像分割成两部分分别处理,然后从各部分的四个边界向内推进搜索,当找到一行或列的像素当中黑色像素占比超过设定阈值时,将该行或列作为矩形边界;
(4)根据矩形的各个边界位置,可以分别计算出矩形的4 个角点,得到原始渐变图主区域对应矩形以及颜色棒矩形。
需要注意的是,如果原始图像中的矩形边界宽度占据多个像素时,需要将检测出来的矩形边界向内推移,以使得矩形准确框选目标区域。
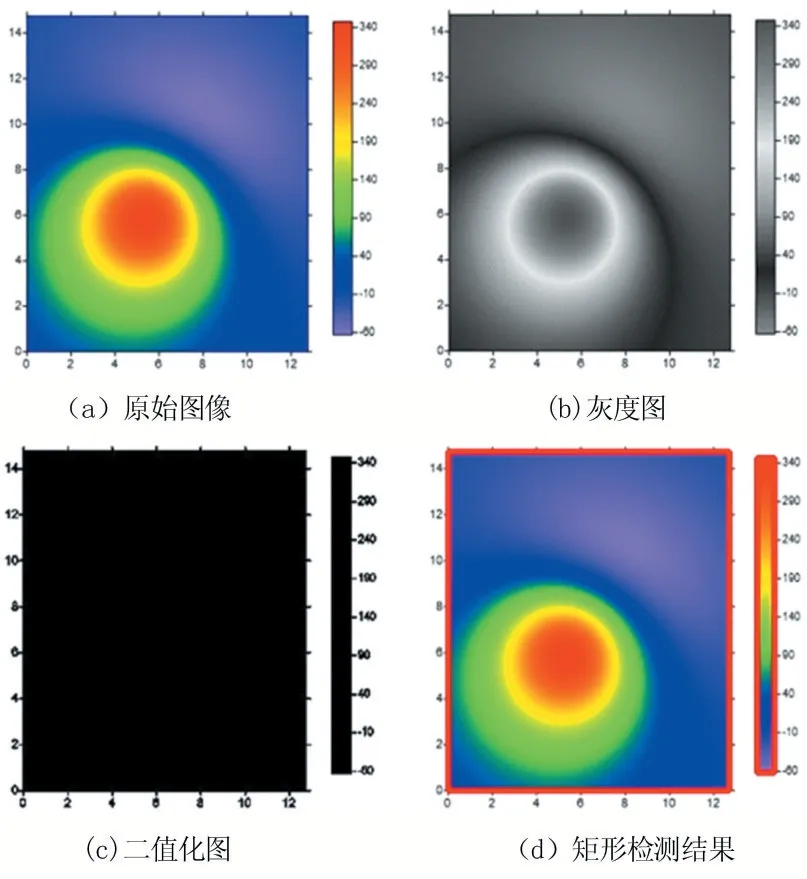
图2 矩形检测过程
1.2 建立映射表
上一步骤识别出来的颜色棒区域反应的是颜色到数值的映射关系,结合颜色棒的最大最小值,可以将颜色棒还原成数值到颜色的映射表,识别过程如下:从下向上遍历颜色棒各像素点,将各个像素点的RGB 颜色值映射到具体数值,形成颜色到标量值的映射关系表。
通过OpenCV 载入渐变图所在的矩形区域,可以读取指定像素点的像素坐标及其颜色,假设某像素点的颜色为(r,g,b),距离颜色棒底部高度为hpixel像素,已知颜色棒对应数值的最小值为Vmin,最大值为Vmax,颜色棒高度为Hpixel像素,根据差值可以计算得到该颜色(r,g,b)的对应数值为:

最终建立的颜色映射表形式如表1。
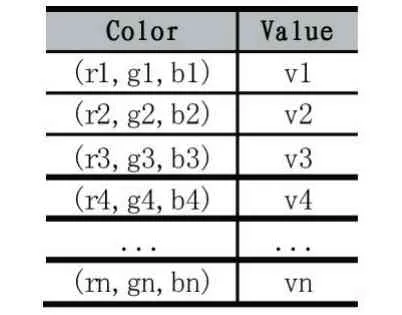
表1
1.3 离散点识别
离散点识别的过程是遍历渐变图主区域中的各个像素点,根据像素点的像素坐标位置及颜色值,结合已经建立的颜色映射表,将颜色值转换为标量值的过程。
假设渐变图矩形的像素宽度为Wpixel,高度为Hpixel,横坐标范围为(Xmin,Xmax),纵坐标范围为(Ymin,Ymax),假设某像素点的像素坐标为(xpixel,ypixel) ,其颜色值为C(r,g,b),根据颜色值去遍历已建立的颜色映射表的各个颜色区间,可以确认出它所处的映射表区间
将该点的像素坐标换算成真实物理坐标为:

而该点的颜色值对应的标量值为:
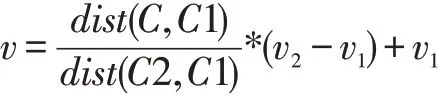
其中,|C2-C1|,表示两种颜色之间的“距离”,通过颜色三分量可以计算得到:

当将渐变图主区域内的各个像素点都识别出其对应的坐标及标量值之后,整个渐变图已经被还原成一个个离散数据,示例如下,每行存放一个离散点的坐标及对应标量值:
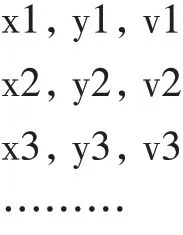
1.4 数据网格化
离散数据并不是最初成图或进行科学计算的常用数据格式,因此还要将识别后的各个散点值重新组织生成二维网格化数据文件。
以比较常用的Surfer 二维空间网格化数据格式(*.grd)为例。这种数据格式头部包括文件头(DSAA)、X及Y 方向点数、X 方向最小与最大值、Y 方向最小与最大值、标量的最小与最大值,然后是网格内各点的标量值。因此,只需要遍历各个离散点,根据散点的坐标,将散点的标量值放在二维矩阵的对应位置上,即可生成二维网格化数据(*.grd)文件,其格式如下:
DSAA
列数 行数
x 最小值 x 最大值
y 最小值 y 最大值
v 最小值 v 最大值
第1 行标量值
第2 行标量值
…
第n 行标量值
2 异常处理
当原始图像中有等值线、数字标注或其他符号标注时,标注所在位置的像素点就很难通过映射表还原成最初的标量数据,对于这种情况,可以暂时不去识别这些不能识别的像素点,而在网格化环节上通过数据插值的手段将这些空缺位置的值补上。
二维数据插值的方法在理论研究和工程计算中都有着广泛的应用,比较常见的有拉格朗日插值法、牛顿插值法、等距结点插值法、有理函数插值法、三角插值法以及样条函数插值法等,它们的共同特点是利用与待计算点位置接近的多个已知数据点,构建插值函数来计算出插值点的函数近似值。除此之外,还有克里金(Kriging)插值法,由1951 年南非采矿师D.G.Krige提出,它是对空间分布的数据求解线性最优、无偏内插估计的一种方法,相对前面的算法,金克里金插值不仅考虑到了待计算点与已知数据点之间的关系,还考虑到了变量的空间相关性,与反距离加权法相比具有明显优点[4]。其实,克里金插值法在数据补全和图像修复方面已有了很多应用,蔡占川、姚菲菲等人提出的基于克里金插值法的图像修复方法在油画修复方面获得了很好的修复效果[5]。
因此,本次研究中以克里金插值来试验数据插值对数据还原的效果。
3 实验结果
以某二维网格数据为例,它的横轴范围为[0,12.75],纵轴范围为[0,14.75],标量数据的范围为[-62.86,347.33],将该数据生成渐变图如图3(a)所示,然后对生成的渐变图图像进行上述数据还原操作得到还原后的网格数据结果,还原结果成图如图3(b)所示,还原结果从整体上看与原始数据相差并不大,我们进一步将还原网格数据与原始网格数据做差值计算的结果成图如图3(c)所示,可以看出原始数据变化大的地方还原结果误差更大,两者相差最大值5.5,误差约1.33%,还原数据非常接近原始数据。

图3 渐变图还原结果
我们将图3(a)中的渐变图加上等值线和数字标注得到图4,然后对生成的渐变图图像进行数据还原操作,等值线以及数字标注等无法识别的地方我们不去识别,后续再通过克里金差值补充不能识别的地方,还原结果成图如图4(b)所示,可以看出即使存在干扰像素,还原结果从整体上看与原始数据也相差不大,我们进一步将还原网格数据与原始网格数据做差值计算的结果成图如图4(c)所示,可以看出两者相差最大值9.3,误差约2.26%,还原数据非常接近原始数据。
4 结语
在二维网格数据生成渐变图的基础上,分析如何从渐变图反推出原始网格数据,并解决了图像中存在等值线、数字、标注影响图像还原的问题,结合OpenCV图像处理库编程能够快速自动的实现从渐变图还原出原始网格数据,且最终的还原数据误差很小,能解决数据缺少或者获取数据成本和难度高的问题。

图4 带标注渐变图还原结果

