深度学习在PM2.5 预测中的应用
贾春光
(云南财经大学统计与数学学院,昆明650000)
0 引言
近年来,中国工业化、城市化以及经济的快速发展,导致中国各大城市的空气污染越来越严重,特别是空气中的PM2.5 已经严重影响到了人们的正常生活。PM2.5,也称细颗粒,通常指的是直径小于2.5 微米以下的颗粒物。
针对PM2.5 的建模和预测问题,Xiao Feng[1]用人工神经网络(ANN)去预测PM2.5——基于空气运动轨迹的地理模型,利用小波变换将PM2.5 的时间序列拆分成规律性更强的子序列,在利用ANN 分别对它们训练独立的模型。王静等人[2]通过支持向量机回归算法对MODIS 遥感气溶胶浓度分析数据与AERONET 地面传感网络的PM2.5 浓度数据,进行了拟合运算,减少了空-地数据不匹配的问题:这种利用卫星数据直接读取及预测大气颗粒物浓度的变化趋势的方法,对遥感大气预测平台的整合具有重要意义。江苏大学孙永霞[3]将关注点放在各个影响因子与全年雾霾总天数之间的关系上,提出了一种主成分分析法并辅以BP 神经网络的预测模型,一定程度上能准确预测全年总雾霾天数,对政府治理成果、重大政策制定具有指导意义。成都信息工程大学颜玉倩,朱克云等人[4]针对PM2.5 浓度预测,应用逐步回归对成都以及附近地区的一次雾霾发生进程进行测试,较为准确地预测了雾霾等级。
在国外,西班牙马德里大学(Madrid)的Esteban Pardo(B)和Norberto Malpica 基于深度神经网络[5],应用LSTM(Long Short-Term Memory Networks)模型构建了用于预测未来24 小时NO2浓度的预测系统,包括连续12 个小时的污染物浓度值作为训练系统输入,包含两个LSTM 层,其次是两个Dense 层,LSTM 层含有512个隐藏层单元,总的测试RMSE 是10.54ug/m3,并比较了对应的CALIOPE 预测系统。美国加州伯克利大学(The University of California,Berkeley)的Vikram Reddy等人[6]基于北京污染与气象信息的时间序列数据,利用LSTM 模型基于递归神经网络(RNN)作为预测未来污染物对的框架[7],分析大规模的长时间序列数据,提出相关的序列依赖性,并训练特定的规模。
本文将传统的时间序列模型和LSTM(长短记忆网络)模型引入到PM2.5 的预测之中,并对实验结果进行了分析和总结。
1 传统的时间序列模型
传统的时间序列预测方法大都基于统计理论,通过构建适当的数学模型来拟合历史时间序列曲线,而后依据所建立的模型来做预测。本文主要介绍的是ARIMA 模型。
求和自回归平均模型的公式如下:

具有如上结构的模型称为求和自回归平均模型,简 记 ARIMA (p,d,q) , 其 中 ∇d=(1-B)d;Φ(B)=1-φ1B-…-φpBp,为平稳可逆ARMA(p,q)模型的自回归系数多项式;Θ(B)=1-θ1B-…-θqBq,为平稳可逆ARMA(p,q)模型的移动平滑系数多项式。
2 深度学习
深度学习是机器学习领域中的一个分支,它的主要目的是从大量的数据中找到某种规律。深度学习强调从连续的层中进行学习,是多层级联的层级结构,每一层中许多非线性单元用于特征抽取和转换,下一层的输入是上一层的输出,每深一层表示对数据更深的抽象。
近几年,深度学习在实践中,尤其是人工智能技术方面取得了革命性的突破和进展,已经被广泛应用于图像分类、语音识别、手写文字转录、机器翻译、语音转换、自动驾驶等各个领域,在这些方面的表现深度已经可以媲美人类,甚至超越人类。
2.1 循环神经网络
在现实生活中,有一种数据是与先后顺序有关系的,如语音数据、翻译的语句等。对于序列数据,可以尝试在隐藏层中加上一层自循环层,这就形成了循环神经网络(Recurrent Natural Network,RNN),它的基本机构如图1。

图1 循环神经网络的结构
其中X 是输入的变量,U 是输入到隐含层的权重矩阵,W 是状态到隐含层的权重矩阵,S 为状态,V 是隐含层到输出层的权重矩阵,O 是输出的结果[13]。从图1 不难看出,它的共享参数方式是各个时间节点对应的W、U、V 都是不变的,通过这种方法实现参数共享,同时大大降低参数的数量。
2.2 长短时记忆网络
长短时记忆网络是一种特殊的RNN,它能够学习长时间依赖。它们由Hochreiter&Schmidhuber(1997)提出,后来由很多人加以改进和推广[13]。
LSTM 的循环结构如图2。

图2 LSTM循环神经网络的结构
其中带箭头的黑线表示数据流向,输入的数据为向量形式,粉红色圆圈表示两个数据所做的向量操作,黄色方框表示数据向量要做的映射,黑线分成两个表示数据向量有两个用处。
3 评价指标
本文中用到了三个常用的评价指标:均方误差根(RMSE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)。三个指标的评价公式如下:

其中,n 为测试样本的总量,yi为第i 个数据点的真实值,为第i 个数据点的预测值。
4 数据来源及预处理
本次数据来源于中国质量分析监测平台,数据集的详细情况见表1。

表1 空气质量数据集信息
该数据集一共有1530 个时间点的数据,涵盖了2015 年1 月1 日开始到2019 年3 月10 日结束时昆明市空气质量指数信息。每个时间点以日为单位。实验中将最后的153 个时间点的数据取出来作为测试点,来对模型进行测试。
本文主要是针对PM2.5 进行建模和预测,首先看一下PM2.5 浓度在数据集中的表现。从图3 中可以看出,这是一个有周期性规律的时间序列,并且各观测点间的方差似乎是稳定的。

图3 昆明市2015年到2019年每日PM2.5浓度
接下来看一下昆明市PM2.5 浓度后一日相比于前一日的增长率,如图4。

图4 昆明市2015年到2019年每日PM2.5浓度的增长率
其中,上述蓝色的点代表后一天比前一天PM2.5的浓度高,绿色的点代表后一天比前一天PM2.5 的浓度低,从图中可以看出,PM2.5 的增长率是下降的天数的多,上升的天数少,说明昆明市的空气质量正在好转。
最后看一下昆明市PM2.5 浓度后一年相比前一年的增长率,如图5。

图5 昆明市2015年到2019年每年PM2.5浓度的增长率
从图5 可以看出,从2015 年到2018 年之间,昆明市PM2.5 浓度的年增长率都是负的,说明PM2.5 的浓度每年都会减少,但近几年下降的幅度都在不断减少。
5 模型的建立
5.1 传统时间序列模型
建立ARIMA 模型的步骤包括:
(1)确保时序是平稳的;
(2)选定可能的p 值和q 值;
(3)拟合模型;
(4)评估模型;
(5)预测。
首先在拿到一组数据后,需要判别其是否平稳,本文使用的是ADF 检验,即单位根检验,检验结果显示p值为0.01,序列是平稳的。
在得到平稳的时间序列后,可以通过ACF 图(自相关函数图)和PCAF 图(偏自相关函数图)来选择备选模型,确立模型各个参数,但这种观察方式,有时会带来极大的误差,使判别模型的预测效果并不是十分的理想,因此,在定阶的过程中常常使用AIC 或者是BIC 的方式,本文采用了AIC 自动定阶算法,算法的思想是通过判断不同的p 和q 的取值,从而算出不同的AIC,找到使AIC 值最小的p 和q 的组合,即为ARIMA模型的最优阶数。最后,函数选定ARIMA(2,0,3)。
最后直接将模型应用到测试序列中,函数返回了模型的2 个回归系数分别为1.263、-0.2767;3 个移动平均系数分别为-0.5385、-0.2615、-0.072。最终ARIMA(2,0,3)的表达式如下:
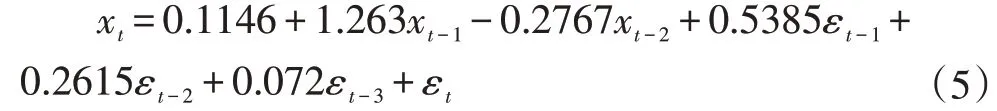
模型确定后,可以用RMSE、MAE、MAPE 来评价模型,它们的值分别为8.657833、6.528301、25.4%。
最后看一下模型在测试时间数据上的表现,如图6。

图6 ARIMA模型的预测值和真实值
从图6 可以看出,预测的效果并不是很理想。测试数据模型的RMSE、MAE、MAPE 分别为8.737107、7.182098、36.46%。
5.2 LSTM模型
本文构建的LSTM 模型主要是在Keras 平台上进行的。
(1)单变量预测
首先只用PM2.5 这一列数据进行建模,接下来对LSTM 模型各个超参数进行如表2 设置.

表2 单变量LSTM 模型的参数设置
批次大小表示每次迭代需要的样本数量,迭代的次数可以看做训练集学习的次数,时间窗口可以看做滞后阶数,当时间窗口为1 时表示模型用上一时刻的数据去训练下一时刻的数据,输出维度表示LSTM 层神经元的个数。
其中激活函数RELU 的表达式如下:

在拟合好模型后,模型在测试样本上的表现如图7。
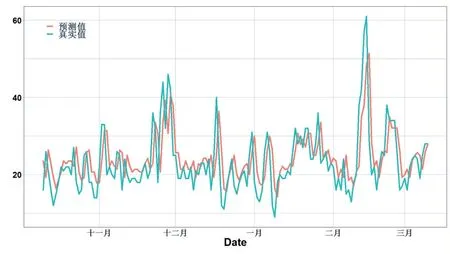
图7 单变量LSTM模型的预测值和真实值
从图7 可以看出来,预测效果相较于ARIMA 模型要好一些。测试集的RMSE、MAE、MAPE 分别为6.59、4.96、23.7%。比ARIMA 模型的精度要高。
通过图7 可以发现,测试结果与原始数据出现了“平移错位”,出现了这种情况的主要原因是模型没有抓住原始数据“季节性”的特点。因此,改变look_backs设定值,表3 展示了不同设定值的测试数据的误差。

表3 不同时间窗口模型的评价指标
当时间窗口为3 或者12 的时候,预测的结果较好。当时间窗口大于12 时,预测精度就会有一个明显的降低。
(2)多变量预测
本文收集的数据还有其它空气质量指标,例如AQI(空气指数)、PM10(可吸入颗粒物)、SO2(二氧化硫)、CO(一氧化碳)、NO2(二氧化氮)和O3_8h(臭氧每8 时平均浓度),这些指标或多或少的也会影响PM2.5的浓度。
在建立模型前,需要对数据进行标准化处理,本文采用的是最大值-最小值法,公式如下:

其中xmax为样本变量中的最大值,xmin为样本变量中的最小值。
接下来对这些数据应用LSTM 模型,参数设置如表4。

表4 多变量LSTM 模型的参数设置
在拟合好模型后,最后看一下模型在测试集的表现,如图8。
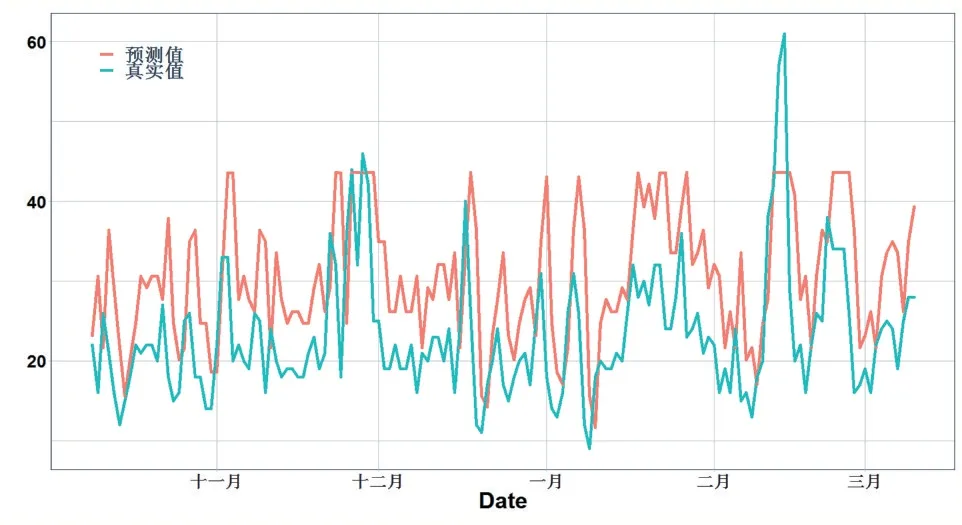
图8 多变量LSTM模型的预测值和真实值
从图8 可以看出,多变量LSTM 模型没有了“平移错位”的现象,预测趋势也与原始数据相对吻合,但误差较大。造成这种误差偏大的原因可能是LSTM 层的维度造成的,不同维度模型的精度如表5。

表5 不同维度模型的评价指标
从表5 可以看出,随着输出维度的增加,模型的精度在逐步降低。
6 结语
本文基于昆明市的空气质量监测数据,将最近流行的深度学习内容应用到PM2.5 浓度的预测中,本文从单变量和多变量两个方面上应用LSTM 模型,单变量LSTM 模型的误差较小,但会出现“平移错位”的现象;多变量LSTM 模型不会出现“平移错位”的现象,但误差相对较大。LSTM 模型很好地解决了梯度消失和梯度爆炸的问题,相比传统的时间序列模型具有较好的学习能力,从而使得模型的预测效果更好。

