基于神经网络的天气发生器
朱思远,张宸豪,吴邪,耿耀君,杨龙
(西北农林科技大学信息工程学院,咸阳712100)
0 引言
天气是农业生产的主要决定因素。在许多不同的尺度上,需要天气数据来解决各种各样的问题[1]。通常,计算参考蒸发蒸腾、优化灌溉策略等问题直接使用实际观测数据进行运算,但在研究地区天气数据缺失的情况下,模型将使用天气发生器生成所需数据[2]。虽然我国已有一些关于天气发生器应用的研究,但所使用的模型需要长期的日气象数据作为输入,这使得该模型在气象数据不足或缺失的地方应用有限。
BP(Back Propagation)神经网络是一种多层前馈神经网络模型,可用于拟合任意复杂的非线性函数[3-4]。神经网络具有良好的鲁棒性、联想记忆、高容错性和信息并行处理能力,被用于多种任务的函数拟合[3]。
本文提出一种基于BP 神经网络的天气发生器模型,可以根据12 个月的月平均天气数据,模拟生成365天的逐日天气数据。河南省南阳气象站从1990 年到2004 年的实测天气数据被用于训练网络模型,使用2005 年到2009 年的数据进行模型验证。
1 基于BP神经网络的天气发生器
1.1 网络结构
本文使用的BP 神经网络结构如图1 所示,由输入层、全连接层、批量归一化层(Batch Normalization,BN)[5]和激活函数组成。

图1 网络结构
第一层输入层InputLayer,是一个全连接层,形状为(None,6,12),用于接收经过预处理的6 个不同天气变量12 个月的平均值(取值在[0.,1.]之间),预处理的详细步骤见1.3。这里的None 不取定值,可表示任意正整数。
接下来,输入层的数据会被输入到Dense 层,Dense 层是一个全连接层,形状为(None,6,128),其中128 是根据经验选择的。输出的数据经过ReLU[6]的激活,引入非线性因素。经过激活的数据会进入批量归一化层,在这里添加批量归一化层是为了:①防止过拟合;②减少对网络初始化的依赖;③解决梯度弥散[5]。
BatchNormalization 层后接一个形状为(None,6,365)的Dense 层,用于产生6 个变量365 天的逐日天气数据,Dense 层的输出经过Sigmoid 激活函数,被映射成[0.,1.]间的数据,作为网络的输出。
1.2 数据
本文所用的数据来自中国气象局,包括南阳气象站从1990 年到2010 年的逐日太阳辐射强度、最高温度、最低温度、风速、露点温度、降水量的实测数据。将1990 年到2004 年的数据用于训练模型参数,2005 年到2009 年的数据用于模型的有效性验证。
1.3 数据预处理
首先,为简化问题,将所有2 月29 日的数据剔除,从而保证每年数据的大小相同,得到20×365×6 个数据。然后,将逐日的数据按年份和月份分组,计算每年每月的天气数据的平均值,得到20×12×6 个数据。最后,将得到的月平均数据进行归一化处理,将数据映射到[0.,1.]范围内式(1)。

式中:
x:归一化前的数据
x*:经过归一化处理的数据,x*∈[0.,1.]
min:x 所有取值中的最小值
max:x 所有取值中的最大值
1.4 训练模型
网络中的参数使用的Xavier 初始化[7],从而保证参数梯度不等于0。损失函数使用常用于回归模型的MAE Loss。使用Adam 优化器优化网络参数,其中超参数(学习率等)使用Kingma 等人[8]提供的值。batchsize 设置为15,即每次将15 年的数据送入网络中训练。
2 结果
由于风速(单位m/s)和降水量(单位mm)为非负值,所以需要将模型生成的风速和降水量剔除负值(式2)。

式中:
x:处理前的数据
x*:处理后的数据
将训练结束的模型用于生成2005 年到2009 年南阳站的逐日天气数据,模拟数据与实测数据的逐日对比见图2(生成的模拟数据长度为5×365 天,横坐标跨度较大,为便于展示,图中仅显示2006 年的情况)。可以看到,各天气变量的实测数据与模拟数据的分布大致相同,模型可以很好地刻画出真实天气数据的一些特征。
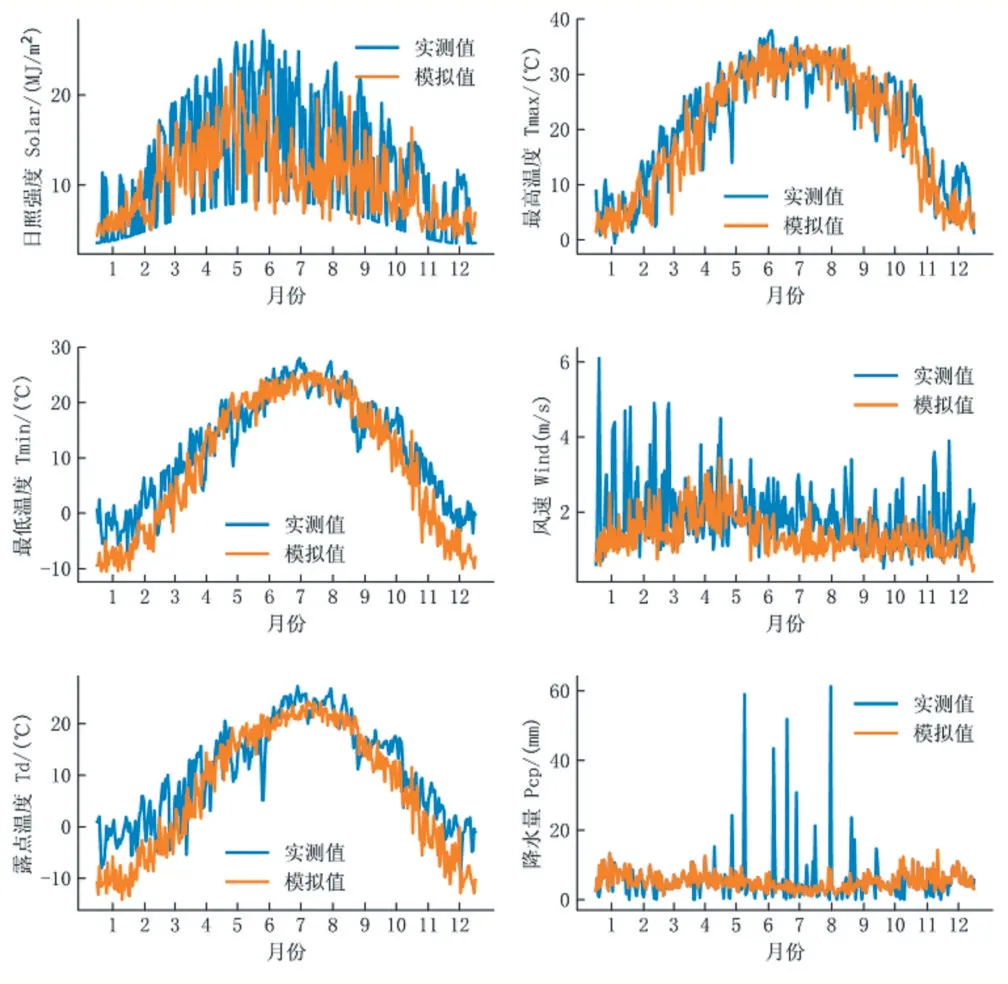
图2 模拟数据与实测数据的逐日对比
2005 年到2009 年的日照强度、最高气温、最低气温、风速、露点温度、降水量的逐日天气数据与实测数据的均方根误差RMSE,在365×5 天内,分别为6.310、5.638、5.743、0.951、7.481、9.172;平均绝对百分比误差MAPE 分别为41.9%、23.6%、7.7%、41.9%、92.9%、208.2%。

图3 实测数据与模拟数据的分散情况(左:实测数据;右:模拟数据)
为了进一步比较两组数据的分布情况,使用箱形图可视化显示实测数据与模拟数据的分散情况(图3)和模拟数据相对于实测数据的绝对误差(图4)。在图中,异常值(绿色圆圈)被定义为大于QU+1.5×IQR 或小于QL-1.5×IQR 的值。其中QU是上四分位数,QL是下四分位数,IQR 是QU和QL的差。结果显示:①除降水量外,各变量的实测数据与模拟数据的分布情况大致相同;②由于极端降水的不确定性,模型对于降水的模拟效果不是很理想。

图4 模拟数据相对于实测数据的绝对误差
下面,分析上述误差存在的原因:
(1)本文设计的神经网络模型过于简单,对于各变量内和变量间的约束条件过少;
(2)本文仅分析了南阳气象站20 年的数据,训练数据与验证数据过少;
(3)本文简单地选取回归分析常用的MAE Loss 作为损失函数,而由于极端气候的不确定性,模型对于极端气候的拟合效果不是很好。对于天气发生器的任务,可以定制相应的损失函数,进行模型训练,使之产生的数据更加接近真实分布,这方面还有待进一步研究。
3 结语
本文将神经网络应用于天气发生器,并使用南阳气象站的天气数据进行模型有效性验证,初步探索了神经网络在天气发生器方面的应用。实验结果表明,该模型可以较好地刻画出真实天气数据的一些特征,为天气发生器模型提供了一种具有参考价值的拟合方法。

