基于风电系统阻抗变化规律的最大功率点跟踪控制研究*

曾林滨，李国良，李 明，冯志康，杨麟,2

(1.云南师范大学 太阳能研究所,云南 昆明 650500；2.云南师范大学 物理与电子信息学院,云南 昆明 650500)

风能是一种清洁的可再生能源，分布范围广，蕴含量巨大.风力发电是风能的主要利用形式，如何最大限度地捕获风能是风力发电系统首先要解决的问题.根据实时风速调整风力发电机的风轮转速，保证风力发电机始终运行在最大功率点(MPP)上，是实现系统高效运行的关键[1].目前被广泛使用的最大功率点跟踪(MPPT)控制方法包括最佳转矩控制法[2]、最佳叶尖速比法[3]、功率信号反馈法[4]和HCS法[5-14]，HCS法又称为扰动观察法(P&O).许多学者已经对HCS算法的优化进行了大量研究，通过智能控制搜索步长精度，有效提高了HCS追踪速度，解决了MPP附近的振荡问题.但是，HCS算法需要通过改变控制器阻抗实现MPPT，而少有人考虑到控制算法在实际风电系统中的应用效果以及系统其他负载阻抗的变化对算法的影响.本文针对现有HCS算法的缺陷，设计了一种基于系统阻抗变化规律的优化HCS算法，从而提高了系统的风电转化效率.

1 MPPT控制原理

1.1 MPPT控制性能评价指标

风轮从分布式风能中捕获的瞬时风功率Pw和总能量Qw为：

(1)

(2)

式中，ρ—空气密度，kg/m3；A—风轮扫掠面积，m2；vi(i= 1,2,…,n)——瞬时风速，m/s；ti(i= 1,2,…,n)—不同风速对应的起始与终止时间，s.

风轮输出的机械功率PM为：

(3)

式中，CP(λ)—风能利用系数，风轮将风能转化为机械能的效率，其表达式为：

(4)

(5)

式中，β—桨距角，系统所用PMSG为定桨距风力发电，故桨距角β固定不变.λ—叶尖速比，是用于表示风力发电机特性的一个重要参数，是叶片尖端速度与来流风速的比值，其表达式为：

(6)

PMSG输出的交流相电流、相电压和平均功率值：

(7)

式中，φ—相电压与相电流间的相位差.同时，PMSG的能量传递效率(即风电转化效率)可表示为：

(8)

根据式(8)可知，通过测量风速、风轮转速和交流电功率，能够计算出风能利用系数和风电转化效率，进而得出PMSG的传递效率，该参数是评价MPPT控制效果好坏的关键指标.

1.2 HCS算法原理

风电热泵制热及压缩制冷系统的电路拓扑图如图1所示.

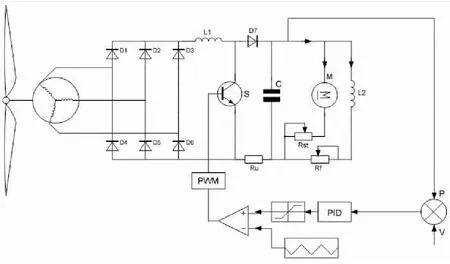
图1 系统电路拓扑图Fig.1 Circuit topology of the system

系统由PMSG、三相整流桥、升压变化器、控制器和直流变速压缩机组成.三相整流桥由三组对称二极管组成，二极管在单一周期内只有一组(如D1和D4)导通，通过规律性开闭将PMSG输出的三相交流电整流为直流电.控制器经过HCS算法计算后，输出脉冲宽度调制(PWM)信号至绝缘栅双极型晶体管(图中S)，使DC-DC升压变换器的占空比D改变，进而改变升压变换器阻抗Zbo.系统在运行时，变速压缩机的启动电阻Rst会随压缩机的启动和停止而变化，调速电阻Rf会随输入直流电功率的升降而变化.因此，压缩机整体阻抗Zco在系统运行过程中时刻变化.

系统阻抗与MPPT控制间的关系推导如下：

经实验测试，系统所用额定功率400W的PMSG在不同风速下转速与输出功率间的关系如图2所示.

图中最大功率点处：

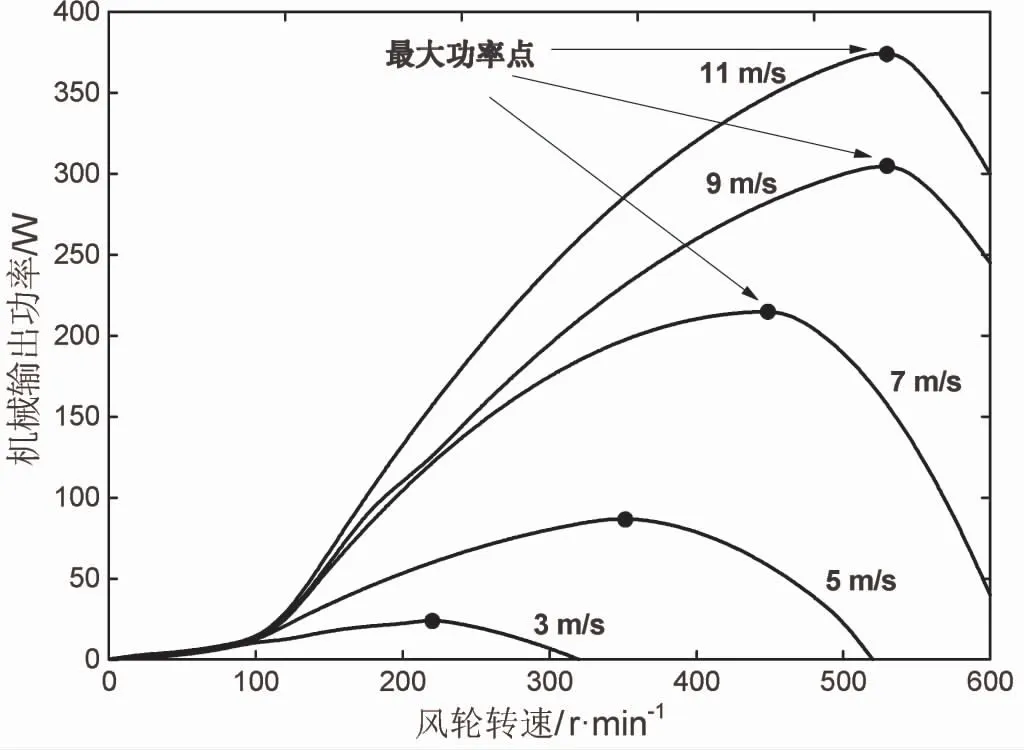
图2 不同风速下的转速-功率对应图Fig.2 Rotational speed-power relationship in different wind speed

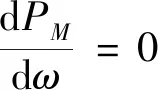
(9)

式(9)可变化为：

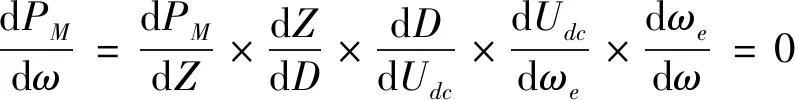
(10)

式(10)中，Z—系统阻抗，Ω.其表达式为：

Z=Zbo,n+Zco,n

(11)

(12)

式(11)中，Zbo,n和Zco,n分别为第n个循环周期时的升压变换器阻抗和压缩机阻抗，Ω.由于二者均不为0，且升压变换器的D不可能为1，所以：

(13)

升压控制器占空比D为：

(14)

式中，Udc—升压前直流电压，V.Ubo—升压后直流电压，V.系统运行时，二者均不为0，所以：

(15)

三相整流桥输出的直流电压Udc与电磁转速ωe成比例关系，所以：

(16)

机械转速ω与电磁转速ωe间的关系可表示如下：

(17)

式中，p—磁极对数，与PMSG型号有关.

由式(10)-(17)可推导出：

(18)

因此，通过调制占空比D，即可改变升压控制器阻抗Zbo，而系统阻抗Z的变化将直接影响PMSG的风轮转速ω，进而改变风轮输出的机械功率PM.

HCS算法原理如图3所示.爬山搜索法通过周期性地改变升压变换器占空比，从而施加转速扰动，通过记录观察扰动后风轮输出功率PM的变化方向，进而确定风轮转速点位于MPP左侧还是右侧，并确定下一步的扰动方向，重复上述步骤直到找到MPP.传统的固定步长HCS算法以恒定的占空比D进行扰动观测，若步长较小，则需要多次扰动才能接近MPP，导致追踪速度过慢；若步长较大，则可能导致系统无法准确找到MPP，在MPP附近反复扰动，循环搜索，导致输出功率的波动.

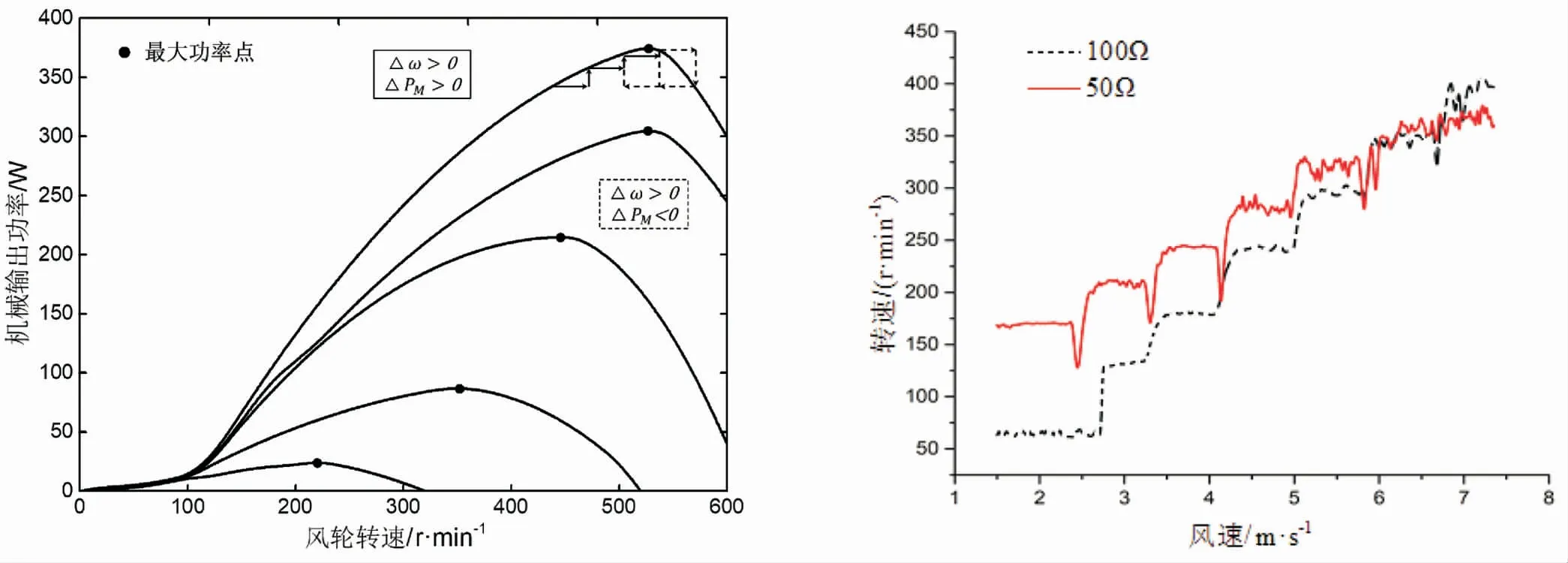
图3 HCS算法原理图 图4 风速-转速对应关系图Fig.3 Principle of HCS algorithm Fig.4 Relationship between wind speed and rotational speed

2 MPPT控制模型验证

为验证前文所推导的MPPT控制模型的正确性，利用室内变频轴流风洞作为模拟风源进行对比实验，探究系统阻抗与风轮转速的对应规律，以及系统阻抗对风电转化效率的影响.

根据图1搭建系统，分别采用50 Ω和100 Ω电阻代替变速压缩机作为系统唯一负载，展开对比实验.同时，对比实验的控制采用同样的传统的固定步长占空比HCS算法，占空比D取固定值0.3.

通过调节风洞频率模拟2-8 m/s风速，50 Ω和100 Ω负载系统在不同风速下的风轮转速变化规律如图4所示.从图中可以看出，当风速低于6 m/s时，风轮转速与风速为正比例关系，在此阶段，随着叶尖速比λ的提高，风能利用系数CP(λ)也不断增加.与100 Ω负载系统相比，50 Ω负载系统由于整体阻抗较低，PMSG内部定子间的电位差较大，导致风轮的平均转速较高.当风速高于6 m/s时，HCS算法开始调节升压变换器占空比，增加系统阻抗，降低风轮转速，以捕获更多风能，提高PMSG输出功率.与50 Ω负载系统相比，100 Ω负载系统由于整体阻抗较高，搜索步长较大，导致转速波动更为剧烈.

表1 PMSG输出功率Table 1 Output power of PMSG

从表1可以看出，低风速时，50 Ω负载系统的PMSG平均输出功率比100 Ω负载系统高出12.4%，高风速时高出16.7%.由于50 Ω负载系统搜索步长较小，功率波动性也较低.

上述实验结果表明，负载阻抗的变化会直接对风轮转速ω产生作用，干扰MPPT控制，从而影响PMSG输出功率，证明了控制模型的正确性.

3 MPPT控制优化及对比研究

3.1 改进的变步长HCS算法

根据上述控制模型推导和实验结果，本文在现有的HCS算法基础上，提出基于系统阻抗变化规律的优化变步长HCS算法，算法流程如图5所示.

控制器的扰动周期为TS，一般可设为0.1 s，控制算法步骤如下：

1)初始化，施加第n步占空比扰动，采集PMSG频率f、交流相电压UAC、交流相电流IAC、控制器电压Ubo、控制器电流Ibo、压缩机电压Uco和压缩机电流Ico信号；

2)根据采集信号计算风轮转速ω、PMSG输出功率PM、控制器阻抗Zbo和压缩机阻抗Zco；

3)判断风轮转速是否变化，即

Δω=ω(n)-ω(n-1)=0

(19)

若风轮转速不变，则设置参数k=0；若风轮转速变化，则设置参数k为：

(20)

4)计算下一步占空比扰动值：

D(n)=k×sign(Δω)×sign(ΔPM)×D(n-1)

(21)

5)跳至步骤1，进行第n+1次扰动.

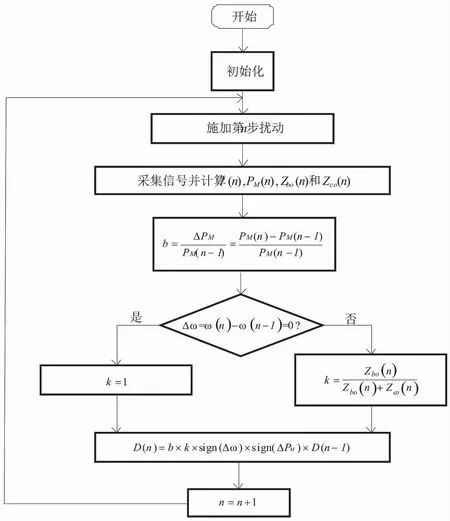
图5 优化的HCS算法流程图Fig.5 Flow of optimized HCS algorithm

上述算法的核心在于根据风轮转速差值判断风轮运行状况，若风轮转速不变，则表示风速稳定，PMSG运行在MPP上；若风轮转速改变，则利用功率差值判断功率点在MPP的左侧还是右侧，并调整扰动变化方向，结合功率变化量和阻抗变化量，设置比例调节参数改变下一步占空比步长，最终实现基于阻抗变化规律的步长自动调整和MPP的智能搜索.

基于上述变步长HCS算法，进行程序编译和关键代码调试，并通过Keil软件将程序烧录至单片机中，使控制器能够根据输入值调节占空比步长.

3.2 HCS优化算法控制效果对比分析

将传统的固定步长占空比HCS算法与优化的变步长占空比HCS算法分别应用到系统中，以变速压缩机作为单一负载在随机变化的自然风况下进行实验.考虑到电气系统与机械系统的动态响应速度相差较大，仅从转速跟踪速度和风电转化效率两方面对两种控制方法进行对比.由于总实验时长过长，无法观察风轮转速的细微变化，因此节选时长约100 s的两端区间对两种控制方法的实际转速与最佳转速进行对比，所选区间内风速均包含了阵风风速和渐变风速变化,结果如图6和图7所示.

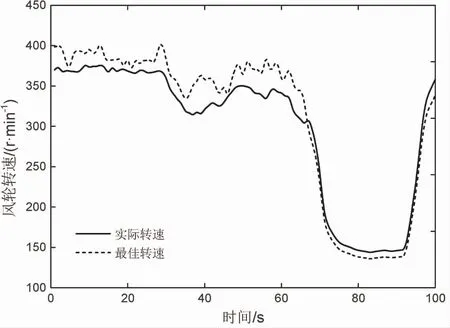
图7 变步长占空比HCS算法Fig.7 Variable step size duty cycle HCS algorithm

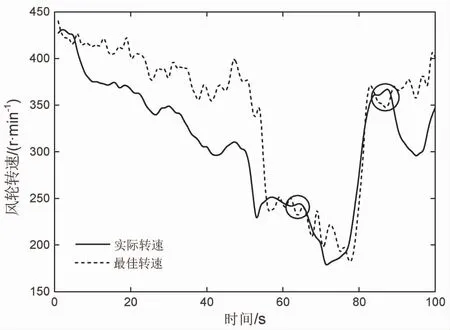
图6 固定步长占空比HCS算法Fig.6 Fixed step size duty cycle HCS algorithm

图6展示了采用固定步长占空比HCS算法时，实际转速与最佳转速的对比.结合PMSG模型，根据实际风速计算拟合得出最佳转速，若实际转速点与最佳转速点重合，则代表着风轮能最大限度地将风能转化为电能.从图6中可以看出，传统的固定步长爬山搜索法的追踪速度较慢，虽然风轮的实际转速与最优转速的变化趋势相同，但是二者间存在较大偏差.如圆圈标识部分所示，受风轮惯性影响，风轮的实际转速变化方向与最佳转速相反.由于占空比步长不可调，即便风速变化较缓，实际功率也在MPP附近振荡，而无法准确追踪到MPP.在自然风况下，通过实验测量统计，采用传统的固定步长占空比HCS算法时，系统平均风电转化效率约为31.6%.

图7展示了采用基于系统阻抗变化规律的变步长占空比HCS算法时，实际转速与最佳转速的对比.从图中可以看出，风轮转速在0-60 s区间内波动较小但变化较快，实际风轮转速虽然无法完全追踪最佳转速，但二者间的差值已大大减少，追踪速度大幅提升；在60-100 s区间内风轮转速呈现快速下降和上升变化，实际转速曲线与最佳转速曲线近乎重合，PMSG全程保持最大功率输出.在自然风况下，经过实验测量统计，采用基于系统阻抗变化规律的变步长占空比HCS控制时，平均风电转化效率提高至40.58%，证明这种控制方法与系统的匹配耦合性较好，能够有效提高MPPT搜索精度和追踪速度.

4 结 论

给出了MPPT控制性能评价指标，推导出MPPT控制模型并验证了其正确性.探明了系统运行时负载阻抗变化与风轮转速、风电转化效率间的对应关系，并根据系统运行时的阻抗变化规律提出一种优化的变步长HCS算法，实现了占空比搜索步长的自动调节，提供了搜索方向错误问题和MPP附近的转速振荡问题的解决方案，有助于提高风能捕获效率，并将平均风电转化效率由31.6%提高至40.58%.