基于AHP-FUZZY法的水下爆破影响区域危险性评价

(1.中国地质大学(武汉) 工程学院，武汉 430074；2.湖南科技大学 岩土工程稳定控制与健康监测湖南省重点实验室， 湖南 湘潭 411201；3.长江重庆航道工程局，重庆 400011)

1 研究背景

作为水下爆破工程中的主要有害效应，水下爆破过程中形成的地震波和水击波对爆破影响区域内建(构)筑物、船舶和鱼类等具有巨大的破坏作用[1-4]。目前，对水下爆破影响区域危险性进行研究的相关内容很少，研究热点为削弱措施及传播特性，如：张社荣等[5]对冲击波在空气和水中的传播特性进行了对比；贾虎等[6]对削减水下爆破有害效应措施提出了新的方法。同时，针对水下爆破作用对象的研究中，研究重点也主要集中于安全判据的探讨：石崇等[7]基于小波理论提出了爆破振动速度-频率作为安全准则的分析技术；阳生权等[8]对爆破地震安全判据中存在的缺陷提出了改进方法。以上研究都丰富了水下爆破理论，但都未对水下爆破影响区域危害等级开展初步分析。梁开水等[9]虽然利用AHP-FUZZY技术在水下爆破安全施工方面展开了研究，却没有将水下爆破影响区域危险性等级化。

鉴于此，本文结合理论分析和工程实例，采用层次分析法和模糊数学构建评价模型，开展水下爆破影响区域危险性等级评价，为工程防护施工提供参考。

2 水下爆破影响区域危险性评价方法

2.1 AHP-FUZZY法基本流程

AHP-FUZZY评价方法结合了由美国运筹学家萨蒂(T. L. Satty)提出的层次分析法和模糊数学中模糊关系合成的原理[10]。该方法刚好弥补了水下爆破影响区域危险性评价中因素繁多、单一定量分析困难等实际问题。AHP-FUZZY方法基本流程如下[11]：①采用层次分析法构建层次结构模型，划分评价等级，得到评价指标的绝对权重；②在模糊数学中选用隶属函数对指标进行量化并构建模糊矩阵，具体步骤如图1所示。

2.2 层次分析法确定指标权重

本文从工程实践经验出发，以水下爆破影响区域危险性评价为决策目标，结合水下爆破影响区域的工程地质、炸药爆炸、地震波和水击波的传播以及评价对象的振动响应，将地质特征、爆破参数、传播特性、安全控制设为一级影响因子。为确保指标之间的独立性，各个指标独立取值于水下爆破不同环节。

2.2.1 指标分析

结合水下爆破特性和区域性评价原理，将上述4种因子进一步细分如下。

2.2.1.1 地质特征指标(A1)

以岩土工程地质为出发点，借鉴其稳定性评价内容，对地质特征指标细分如下：①地层岩性(B1)对振动参数的影响较大，包括不同地层的风化程度、岩石破碎程度等性质；②地形地貌(B2)直观地还原了水下爆破区域内地表以上地质特征，并直接影响水下爆破地震波的传播以及振动响应特征；③不良地质条件(B3)分析是对区域内受水下爆破影响而发生泥石流、滑坡等不良地质现象的概率性分析，许多研究也证明爆破对不良地质作用的产生或复活有直接性的影响[12]。

2.2.1.2 爆破参数指标(A2)

参考工程实例和已有研究成果，爆破设计参数在实际工程中的取值往往差异较大，但经过选取优化后对水下爆破有害效应的影响效果较为明显。将爆破参数指标细分如下：①单段最大药量(B4)是计算水击波峰值压力和地震波振幅的重要参数，具体的取值应考虑实际工程的爆破要求和周围环境；②堵塞长度(B5)的合理性直接影响水下爆破有害效应峰值以及爆破效果，其取值与水下爆破有害效应呈负相关；③延时设置(B6)利用分段起爆的时间差使得各段爆破振动产生干扰叠加，从而达到降低振动强度的目的,文献[13]采用小波包分析振动幅值，本文对优化延时设置的取值主要根据降振率来确定；④孔间距(B7)、孔排距(B8)是为提高爆破质量而进行设计优化的爆破孔网参数；⑤最小抵抗线(B9)的大小对水下爆破振动的强弱以及频率都有影响。

2.2.1.3 传播特性指标(A3)

考虑水域环境对爆破器材以及爆破效果的影响，参考水下爆破形成的地震波和水击波传播特性的研究,对传播特性指标细分如下：①水深(B10)对炸药的爆速和猛度会产生明显的影响，爆速和猛度会随着水压的增加呈一定比例下降，而不同水深下的水压也直接影响水击波压力峰值以及地震波的传播[14]；②相对高程(B11)是影响区域相对于水下爆破区域的高度差，地震波的高程放大效应是不容忽视的研究因素[15]；③爆源距离(B12)是评价影响区域危险性等级最为直接的参数。

注：地层岩性引用文献[17]中的参数，S为志留系；K为白垩系；D为泥盆系；Qn为第四系更新统；N为上第三系；Z为震旦系；J为侏罗系；P为二叠系；C为石碳系；T为三叠系；O为奥陶系；E为下第三系；vδ，ε，δ，βμ，∑分别代表辉长闪长岩、霞石正长岩、闪长岩、辉绿岩和辉绿玢岩、未分的超级性岩

2.2.1.4 安全控制指标(A4)

针对水下爆破作用下评价对象的承受能力，对安全控制指标细分如下：①允许振速(B13)是反映区域内建(构)筑物、道路在水下爆破作用下能承受的最大振动幅度；②频率系数(B14)是为了研究评价对象受水下爆破影响而发生共振的概率性指标，采用fb/fg计算，fb为水下爆破引起的主震频率，fg为研究对象自振频率；③爆破振动持续时间(B15)从1 s增加至50 s的过程中爆破的破坏能力可增大40倍[16]；④冲击波峰值压力(B16)作为水下爆破水击波的最大值，对紧邻的建(构)筑物及岸坡等不良地质体存在巨大威胁。

综合上述观点，采用YAAHP层次分析软件建立影响区域危险性评价等级的层次结构模型，如图2所示。

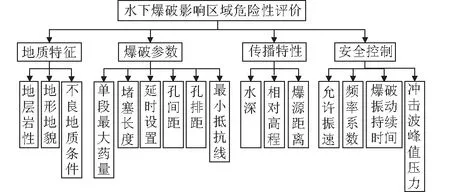
图2 层次结构模型图Fig.2 AHP structure model

2.2.2 划分指标等级

为了更具体、详细地描述水下爆破影响区域危险性，本文采用5级评价体系将危险性等级划分为微度、轻度、中度、高度以及极度5个危险等级，分别对应Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ级。等级边界值参考各评价指标研究成果以及《爆破安全规程》(GB 6722—2014)。16种危险性评价因素与危险等级的对应关系如表1所示。

2.2.3 构建矩阵及其一致性检验

为排除个体主观差异性，本文采用层次分析法中1—9标度法对各级评价指标之间的相对重要性进行定量化描述，邀请了多位学术专家和爆破工程师对各级评价指标进行打分。通过两两比较的方式得到T-A,A1-B,A2-B,A3-B,A4-B5个评价矩阵，最终确定A1—A4，B1—B13相应的权重分值。在YAAHP层次分析软件输出检验评价矩阵的一致性比例Rc的结果中，T-A,A1-B,A2-B,A3-B,A4-B5个评价矩阵均<0.10，矩阵一致性检验满足要求。将构建的矩阵及一致性检验结果列于表2—表6。

表2 T-A判断矩阵及一致性检验结果Table 2 T-A judgment matrix and consistency test result

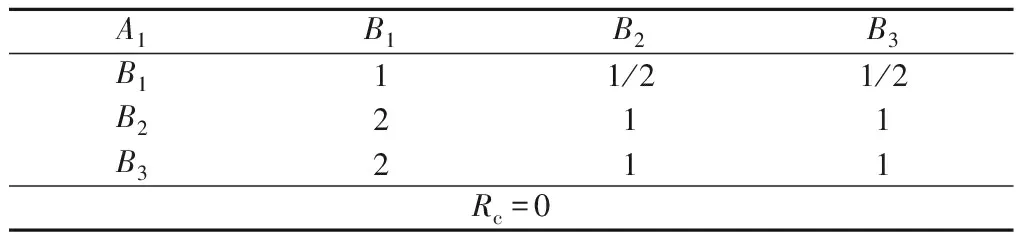
表3 A1-B判断矩阵及一致性检验结果Table 3 A1-B judgment matrix and consistency testresult

表4 A2-B判断矩阵及一致性检验结果Table 4 A2-B judgment matrix and consistency testresult

表5 A3-B判断矩阵及一致性检验结果Table 5 A3-B judgment matrix and consistency testresult

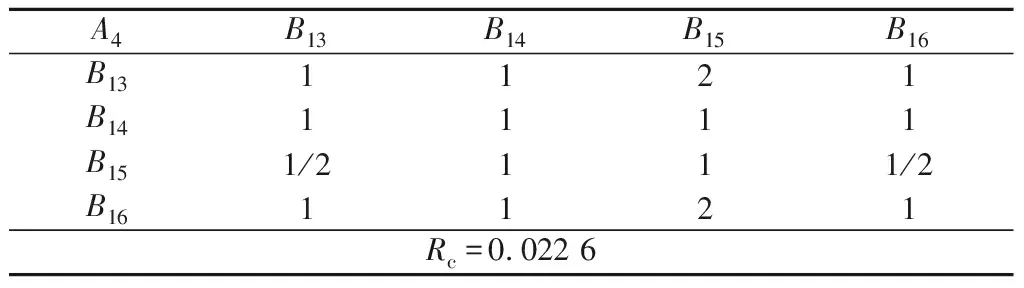
表6 A4-B判断矩阵及一致性检验结果Table 6 A4-B judgment matrix and consistency testresult

2.2.4 绝对权重结果

将总决策目标分层拆分可得到下级指标相对上级指标的相对权重值。为获得最下层指标对总决策目标的独立影响程度，应进一步计算层次总排序的绝对权重值。各级指标绝对权重结果如表7所示。

用向量形式将绝对权重结果表示为：A[0.142 6，0.283 3，0.336 9，0.238 2]；T[0.028 3, 0.056 7, 0.056 7, 0.122 1,0.033 4,0.056 7,0.018 9,0.018 9,0.033 4,0.070 7,0.080 9,0.185 2,0.069 3,0.058 3,0.041 2,0.069 3]。

2.3 模糊数学确定指标隶属度

由表1不难看出，本文给出的区域危险性等级间分界标准虽然清晰简单，但实际数值在边界取值时容易出现模糊状态，而模糊数学(FUZZY)通过选取隶属函数可充分考虑等级划分间的过渡。本文遵循文献[18]中确定隶属函数的原则，对于表1中定量指标，采用岭型隶属函数，依照式(1)构建隶属函数(具体隶属函数略)。

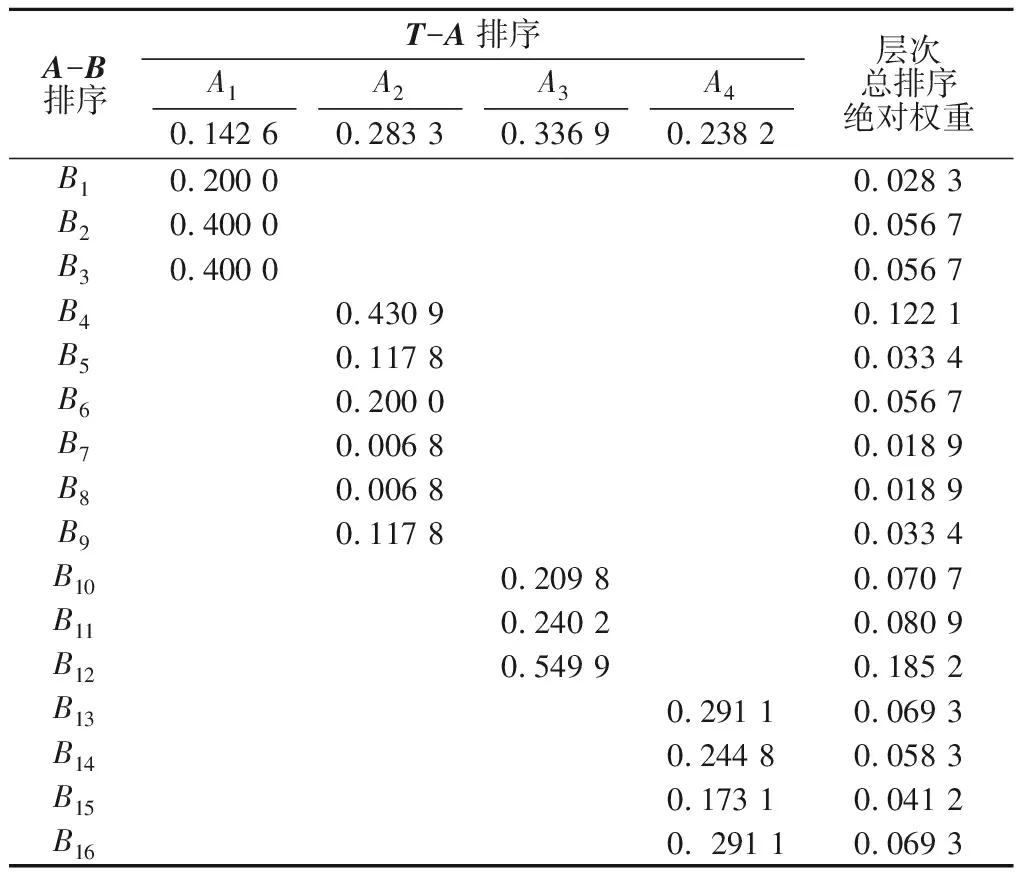
表7 水下爆破各级指标绝对权重Table 7 Absolute weights of indicators for underwaterblasting

(1)

式中ai为危险等级的边界值。

对于表1中定性指标，需要按照相应的准则进行量化，本文采用分级法确定其模糊矩阵，即将指标分为5个等级：优(0.9)、良(0.7)、中等(0.5)、差(0.3)、劣(0.1)。通过赋值标准给出确定的数值，后采用梯形隶属函数，构建隶属函数如下(以微度危险和极度危险为例)：

(2)

式中下标Ⅰ和V分别代表微度危险等级和极度危险等级。

在实际工程应用中，将获得的指标赋值依次代入式(1)、式(2)和式(3)，获得可以反映所有指标隶属度的模糊矩阵R。

2.4 AHP-FUZZY综合评价模型

结合上述步骤，建立AHP-FUZZY综合评价模型，将表1中划分的5个等级和指标论域表示如下：等级论域V={V1，V2，V3，V4，V5}={I，II，III，IV，V}；指标论域U={U1，U2，U3，U4}。其中：Vi为评价等级；Ui为4个评价指标因子，U1为地质特征，包括3个子指标；U2为爆破参数，包括6个子指标；U3为传播特性，包括3个子指标；U4为安全控制，包括4个子指标。

2.4.1 一级综合评价

将绝对权重向量T中所有子指标按Ui域构建4个权重向量Ti，并通过隶属函数构建与评价等级V相对应的模糊矩阵R={r1，r2，r3，r4，r5}。则可求出模糊向量Bi=Ti·ri。

表8 水下爆破影响区域评价指标参数取值Table 8 Values of the parameters of evaluation indicators for underwater blasting

2.4.2 二级综合评价

将模糊向量Bi组成4行5列的模糊矩阵Bk，而总的二级评价结果为：B=A·Bk,式中A为一级指标论域U的绝对权重向量。最后，根据模糊数学的最大隶属度原理选取向量B中最大值以确定区域的危险性等级。

3 工程实例

3.1 工程概况

本文选取长江上游九龙坡—朝天门河段水下炸礁工程作为评价实例。河段长22 km，属于山区河道，流经川南丘陵地带，较山地河道地势相对较缓，河床较为开阔，河道走向迂回曲折，河床宽窄相间。河段沿线环境复杂多变，既有桥梁、道路、房屋等建筑，也有边坡等不良地质体。本文选取位于航道里程675～678 km的砖灶子滩段，沿线有李家沱大桥、道路、民房、厂房等，炸礁区域周围环境分布见图3。

图3 炸礁区域周围环境分布Fig.3 Circumstances around the underwater blasting area

参考施工区域工程勘察资料、技术交底报告、爆破方案等资料，将危险性评价相关参数取值列于表8。

3.2 模型计算

以李家沱大桥北侧的主桥墩计算为例，依照模型计算步骤，将表8中的数据代入隶属函数获得由4个模糊子集构成的模糊矩阵R，以r1为例的矩阵形式如下。

将权值Ti代入Bi=Ti·ri。进行一级综合评价得到模糊向量Bi(以B1为例)，即

可得B1=(0,0.03,0,0.11,0);B2=(0,0,0.13,0.12,0.03);B3=(0，0.01，0.24，0，0.08);B4=(0,0,0.03,0.03,0.17)。将模糊向量Bi组成4行5列的模糊矩阵Bk[B1,B2,B3,B4]，则二级评价向量B为

B=A·Bk=

得B=(0，0，0.13，0.06，0.08)，根据最大隶属度原理，可知李家沱大桥的北侧主桥墩属于中度危险区域。

依照AHP-FUZZY模型，计算得到南桥墩评价向量B=(0，0，0.08，0.11，0.08)；巴滨路评价向量B=(0,0,0.09,0.05,0.12);九渡口公路评价向量B=(0,0,0.09,0.11,0.06)；民房、北岸电厂泵房评价向量B=(0，0，0.09，0.08，0.10)。由此可知该区域内属于轻度危险等级的有南桥墩和九渡口公路，微度危险等级有巴滨路和民房、北岸电厂泵房，中度危险等级有北桥墩。

4 结果验证分析

为验证本文AHP-FUZZY模型的可行性以及准确性，以爆破安全规范中建筑物损害程度为参考标准，采用TCTC-4850型爆破测振仪和国产Blast PRO型爆破冲击波测试仪配以美国PCB产W138A型压力传感器对评价对象开展爆破水击波、地震波等参数的监控测量工作。桥墩、公路及民房的监测布设情况如图4所示。

图4 桥梁墩部和民房及公路监测Fig.4 Monitoring of blasting parameters at bridge pier, residence and road

将模型预测结果与工程实际数据进行对比，对比结果如表9所示。由表9可知，运用该模型对水下爆破影响区域进行危险性评价能很好地对水下爆破作用下影响区域的危险等级进行预测，可提前对受害程度严重的建(构)筑物采取减震孔、气泡帷幕等防护措施，有效提高爆破质量。

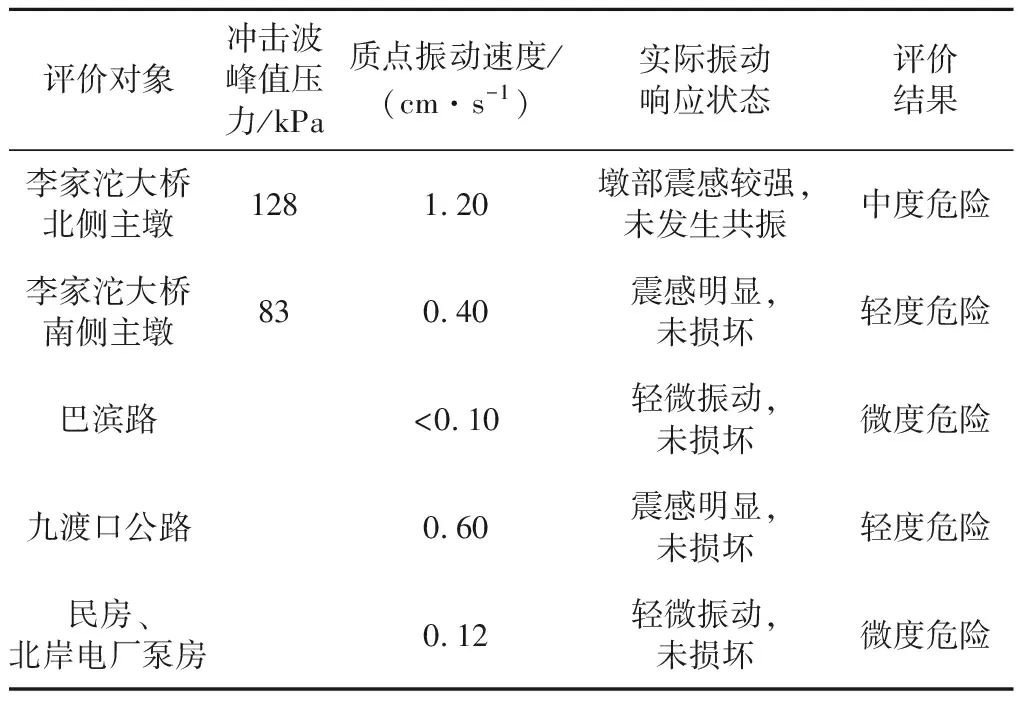
表9 评价结果对比分析Table 9 Comparison of assessment result betweenmodelling and monitoring

5 结 语

(1)水下爆破危害性影响因素较多，采用单一变量难以定量分析。本文基于水下爆破施工中爆炸、传播以及振动响应3个阶段，从地质特征、爆破参数、传播特性以及安全控制4个方面客观地选取了16个水下爆破影响区域危险性评价因子。

(2)针对水下爆破工程存在毗邻环境复杂多样、爆炸过程难以观测等问题，本文建立AHP-FUZZY模型对水下爆破影响区域的危险性进行了定量评价，有效地预测了危险等级。模型中采用较多的评价影响因素参与评判，权重分配与指标量化做到了主观与客观相结合，使评价结果更准确有效。

(3)本文建立的模型实际操作性强，计算结果接近实际施工状态。同时，在工程应用中可通过 与保护对象的实际响应状态进行对比分析等手段不断提升模型的完整性和实用性，为水下爆破防护措施的施工提供 有效的参考。