基于经济增长视角下的地方政府债务研究
——以山东省十七城市为例
陈丽宇
(青岛黄海学院 经济学院 ,山东 青岛 266427)
伴随着我国经济“新常态”的出现,地方政府面临着更多的新压力,作为三大系统性风险之一的地方债务风险进一步凸显。2008年金融危机后的刺激政策,使得我国经济迅速回暖,但另一方面,地方政府债务在推动经济发展和应对经济危机的同时,快速累积的债务规模和不断增长的财政负担,也引发了整个社会的担忧。但是地方政府债务对于地区究竟有什么样的影响,是促进还是抑制,无论是国内还是国际上都没有统一的定论。不少地区政府债务赤字已经严重影响到地方经济的发展,怎样的债务阈值才能够促进经济的持续快速发展以及建立怎样的测度模型来确定两者之间的量化关系从而达到相互促进、相辅相成的效果,这些都是刻不容缓需要解决的问题。
根据文献查阅,国内外学者对政府债务和经济增长关系的研究无论是理论还是实证研究方面都已成熟,其实证分析主要结论有四类:促进经济增长(Delong.B.J and Summers.L.H[1])、阻碍经济增长(Afonso and Jalles[2])、无显著关系(Schclarek.A[3])、存在临界值(Reinhart and Rogof[4]、Ibrahim Dogan and FaikBilgili[5])。虽然都十分关注政府债务与经济增长的关系,但是研究对象大多不是中国,对于地方政府债务对经济增长影响的研究结论并不能完全适用于我国的实际情况。而国内学者对我国地方债与经济增长关系的实证研究相对较少,有学者通过实证分析发现地方政府性债务与区域经济增长之间存在明显的正相关[6],也有学者研究得出政府债务规模增加对区域经济的影响是倒U型的,存在明显的阈值效应[7-8],但对地方债务与区域经济增长的关系,区域差异大多集中在东、中、西部[9],缺少对省市地方政府债务与经济增长的研究,个别省份研究认为地方政府债务对于经济增长有促进作用,但是相关系数较小[10]。山东省作为我国的人口经济大省,对我国经济具有重要的影响。因此,我们以山东省十七城市为例,考察山东省各个城市政府负债对经济增长的影响。通过分析省内不同地区对经济增长的影响,有利于理清不同类型地方政府债务对经济增长的区域影响的差异,从而有助于政府制定合理的政策来促进区域经济增长。
本文的创新点是在借鉴和吸收国内外有关经济增长与政府债务关系研究优点的基础上,一是找出了最适合衡量山东省经济的增长因素指标,对山东省的经济增长与山东省地方政府债务对经济的增长进行总体的分析;二是首次对山东省分区域建立面板数据模型进行了对比分析,找出区域间差异。
1 模型的选取与建立
1.1 理论模型的建立
政府性投资是地方政府债务与经济增长之间影响的重要纽带。根据凯恩斯理论,投资性支出对经济增长促进作用的大小取决于政府投资对私人投资的挤出效应,从而导致不同地区的政府债务对经济的影响存在差异。下面,我们对总体的效应模型进行理论分析。
(1)地方债务对经济增长影响的总体效应模型[11]
我们以生产函数为代表的投入产出模型来分析地方政府债务对经济增长的关系:
Y=AKαLβ
(1)
由于地方政府债务主要是用于资本性支出,那么地方债务和资本支出具有以下关系:
K=D/n
(2)
其中,D表示地方政府债务,n表示地方政府支出占资本性支出的比重。
两边同时除以L得到:
(3)
则人均GDP和人均地方政府债务的关系可以表示为:
(4)

因为影响经济增长的因素有很多,我们以负债率对经济增长的影响为自变量,同时以人均GDP、城镇化率、工业化率、财政赤字、人力资本水平[12]影响经济增长的因素为其他自变量,和负债率组成自变量集,来表示地方政府债务对GDP增长率的影响,建立静态面板数据模型:
yit=c+αXit+εit,i=1…N,t=1…T
(5)
其中,yit表示GDP增长率,Xit表示自变量集,i表示截面下标,t表示时间下标,N表示截面数据个数,T表示时间序列长度。
(2)不同条件下的地方政府债务对经济的影响
假设LM曲线恒定并假设政府购买性支出是通过发行债务,且考虑到中国地方经济中利率的非市场化,利率会直接影响投资。支出的增加引起IS曲线向右移动,均衡利率上升Δr,得到经济的挤出效应为dΔr/(1-β),其中利率对市场投资的影响系数越大,政府支出对私人投资的挤出效用就越大,其对经济的影响就越小。

图1 不同条件下地方政府债务支出经济效应
如图1所示,根据投资对利率的敏感程度划分不同的市场,L地为敏感度较低的区域,其投资的影响系数较小导致IS曲线更为陡峭,而H地的投资影响系数较大,导致IS曲线更为平缓,是敏感度较高的区域。假设政府举债数量相同,即产生的乘数效应相同,即M=ML=MH,则存在以下关系:
(6)
其中,M表示乘数效应,E表示挤出效应,X表示经济效应。由于EH>EL,所以XH (1)模型的优点 面板数据模型是对同一截面单元集的重复观察,能更好地对不同的截面单元在不同时间观察值进行结合,包含的信息量大,增加了自由度,提高了估计效率,从而降低了变量间多重共线性带来的困扰[13]。而且,运用面板数据模型有助于控制变量的个体异质性,一些我们难以衡量或者获得数据的因素无法进入我们的模型时,面板数据可以处理这些不可观测的个体效应。同时,面板数据还便于数据动态调整,从而更精准地刻画复杂的经济行为,使得模型和其结论具有更好的理论意义和应用价值。 (2)指标选取 由于经济体系的构成比较复杂,影响经济的因素有很多,国内外学者对于变量的选取有诸多的讨论和分析。但总的来说,对于被解释变量的选取还是比较一致的。经过查阅大量的文献,我们选取负债率、人均GDP、城镇化率、工业化率、财政赤字、人力资本水平作为影响GDP增长率的主要因素[14]。各个变量符号表示及计算公式如表1所示。 (3)模型的检验 首先,进行单位根检验,发现各变量一阶差分后平稳,如表2所示。 表1 各个变量符号表示及计算公式 表2 单位根检验结果 对本文数据进行协整检验,t值为-3.870 512,通过协整检验则表示经济增长与解释变量之间存在协整关系。 进行Hausman检验,得到P值为0.3358>0.05,接受原假设,在固定效应模型与随机效应模型之间选择随机效应模型。 进行F检验,S1= 0.573287,S2=0.467877,S3=0.567467,S4=0.472895,S5= 0.495889,S6=0.487576,计算得F2=0.783748,小于0.05水平下的临界值,所以接受H2,因此采用混合模型。 前文理论部分分析得出,政府负债对经济增长存在非线性影响,大约是开口向下的二次函数关系,将基本静态模型公式(5)中引入债务的二次方项,得到回归方程 Y=c+β1debt2+β2Xit+εit,i=1,…,N,t=1,…,T (7) 根据搜集到的数据,利用Eviews软件,画出山东省十七个城市政府债务和经济增长的二次曲线拟合图,如图2所示。从图中可以看出地方政府债务对经济增长的影响大概是倒“U”型,类似于开口向下的二次函数,这也间接证明了政府债务对经济的促进作用存在一个临界值,超过这个临界值,地方政府债务将不再对经济增长具有促进作用。但政府部门只要将债务规模控制在一定的范围内,政府债务还是会对经济增长发挥促进作用的。 图2 山东省十七个城市政府债务和经济增长的二次曲线拟合图 根据公式(7)回归模型以及山东省十七个城市政府债务和经济增长的二次曲线拟合图,我们令debt=debt2,得到新的一列变量,然后对各变量进行随机效应混合回归,得到的总体回归结果,如表3所示。 表3 总体回归结果 根据上述随机效应混合的估计结果得到的回归结果如式(8)所示。 Y=3.014121379-0.087575923debt2-3.825358853X1-152.2344459X2+7.60E-07X3+0.232953333X4+3.749 692 657X5 (8) 通过上述回归模型的结果,可以看出山东省十七城市地方政府债务对经济增长的总体影响关系大概是呈倒“U”型,可以看出本文的主要解释变量政府债务对经济增长在一定范围内具有正向相关的影响作用。适当地提高政府债务的规模,可以促进山东省及各市的经济发展,但是超过这个范围政府债务增加,反而抑制经济的增长。也就是说,政府负债对经济增长的促进作用有一个阈值,超过这个阈值,政府债务增加对经济的增长起到抑制作用。 山东省十七城市地方政府债务对经济增长的总体影响大概是倒“U”型,类似于开口向下的二次函数对数据进行面板回归,证明了政府负债对经济增长的促进作用有一个阈值,超过这个阈值,政府债务增加对经济的增长起到抑制作用。为了研究不同地区,政府债务对经济增长的阈值是否相同,我们对山东省的各个地区分别进行了分析。按照地域对山东省进行划分,将山东划分为鲁西北、鲁中、鲁南鲁西南以及山东半岛四个区域,分别对每个区域建立面板数据模型进行分析,并对回归结果进行对比分析。其中,鲁西北指德州、滨州、聊城、东营;鲁中指济南、泰安、莱芜、淄博、潍坊;鲁南鲁西南指济宁、菏泽、临沂、枣庄、日照;山东半岛指青岛、烟台、威海三个地区[15]。 (1)对鲁西北地区的分析 利用Eviews软件,画出山东省鲁西北地区城市政府债务和经济增长的二次曲线拟合图,如图3所示。 根据上述回归模型(7)以及鲁西北地区政府债务和经济增长的二次曲线拟合图,我们令D1=debt2,得到新的一列变量,然后对各变量进行随机效应混合回归,根据随机效应混合的估计得到的回归结果如式(9)所示。 Y=0.884974703434*debt-1.92446883067*debt2+0.0275136109206*X1+24.3292371614*X2+1.45270975412e-08*X3-0.0818446250574*X4-0.144958900139*X5 (9) 图3 鲁西北地区政府债务和经济增长的二次曲线拟合图 从回归结果确定鲁西北地区负债率的阈值为debt=23%,也就是说在负债率不超过23%的情况下,适当地增加负债规模可以拉动该区域的经济增长,一旦超过阈值反而抑制经济。 (2)对鲁中地区的分析 利用Eviews软件,画出山东省鲁中地区城市政府债务和经济增长的二次曲线拟合图,如图4所示。 图4 鲁中地区政府债务和经济增长的二次曲线拟合图 同理得到回归结果如式(9)所示。 Y= 8.58549706947*debt-26.8730746032*debt2-0.010729573796*X1+31.2005812489*X2-2.32973465091e-07*X3-0.213481734197*X4-0.0861726221629*X5 (10) 从回归结果确定鲁中地区负债率的阈值为debt=16.03%,也就是说在负债率不超过16.03%的情况下,适当地增加负债规模可以拉动该区域的经济增长,一旦超过阈值反而抑制经济。 (3)对鲁南鲁西南地区的分析 利用Eviews软件,画出山东省鲁南鲁西南地区城市政府债务和经济增长的二次曲线拟合图,如图5所示。 图5 鲁南鲁西南政府债务和经济增长的二次曲线拟合图 同理得到回归结果如式(11)所示。 Y=8.97850821137*debt-13.0924553626*debt2-0.046923985477*X1+35.1882770711*X2-8.50392497373e-09*X3-0.0746141115071*X4+ 0.0989032244603*X5 (11) 从回归结果确定鲁南鲁西南地区负债率的阈值为debt=38.86%,也就是说在负债率不超过38.86%的情况下,适当地增加负债规模可以拉动该区域的经济增长,一旦超过阈值反而抑制经济。 (4)对鲁中地区的分析 利用Eviews软件,画出山东省胶东半岛地区城市政府债务和经济增长的二次曲线拟合图,如图6所示。 同理得到回归结果如式(12)所示。 Y=4.94384579068*debt-19.9493307905*debt2-0.00932675303056*X1+8.3825500942*X2-1.81772682558e-08*X3-0.0540857509597*X4-0.085373041765*X5 (12) 图6 胶东半岛地区政府债务和经济增长的二次曲线拟合图 从回归结果确定胶东半岛地区负债率的阈值为debt=12.3%,也就是说在负债率不超过12.3%的情况下,适当地增加负债规模可以拉动该区域的经济增长一旦超过阈值反而抑制经济。 通过对分区域政府债务和经济增长关系结果的分析得出,山东省四个区域的负债规模的阈值存在差异,其中鲁南与鲁西南地区和鲁西北地区的负债规模阈值较高;胶东半岛和鲁中地区负债规模阈值较低。这是由于胶东半岛处在沿海地区,开发较早,旅游业、海洋业是其特色,交通发达,有很多跨国公司,是山东省经济的龙头,所以其负债率阈值比较低;鲁中地区大力发展旅游业,加上省会城市济南的存在,济南在山东省经济版图中占据一定地位,负债率的阈值也相对较低;而鲁西北属于欠发达地区,其负债率阈值较大,提高负债规模是为了加强地方建设,提高经济的增长;鲁南鲁西南地区城市分布密集,城市间经济联系和合作程度低,交通不发达,加强地方基础设施建设十分迫切,增加举债、提高负债率是必然的结果,负债率的阈值最高。 山东省四个区域间发展不平衡,省内经济发展格局呈现出东部沿海和鲁中省会城市经济较发达的特征,应针对不同区域的实际情况,制定相适应的经济政策。山东省的经济增长动力主要来自于投资和消费拉动,全省固定投资规模最大的前五位城市中四个城市属于胶东半岛和鲁中地区,并且进出口也对胶东半岛的经济增长有一定的拉动作用,经济发展水平较高,有利于债务融资,保持适当的债务规模可以拉动地方经济发展,但仍要警惕超出阈值后的负面影响;而对于欠发达的鲁西北和鲁南鲁西南地区,固定资产投资规模整体偏低,消费的拉动作用也不明显,财政实力偏弱,对传统产业依赖度较高,在推进供给侧改革时需要大量财力保障。目前其举债的绝对规模不大,通过分析,政府性债务在未超过阈值时能拉动经济增长,因此不能切断债务融资这个渠道,否则会加剧资金压力。但是,由于其经济实力较弱,对债务的承担能力较差,不能盲目增加地方政府债务,要注意减少存量债务以提升该地区的财政实力,降低负债率。1.2 面板数据模型的选取与建立

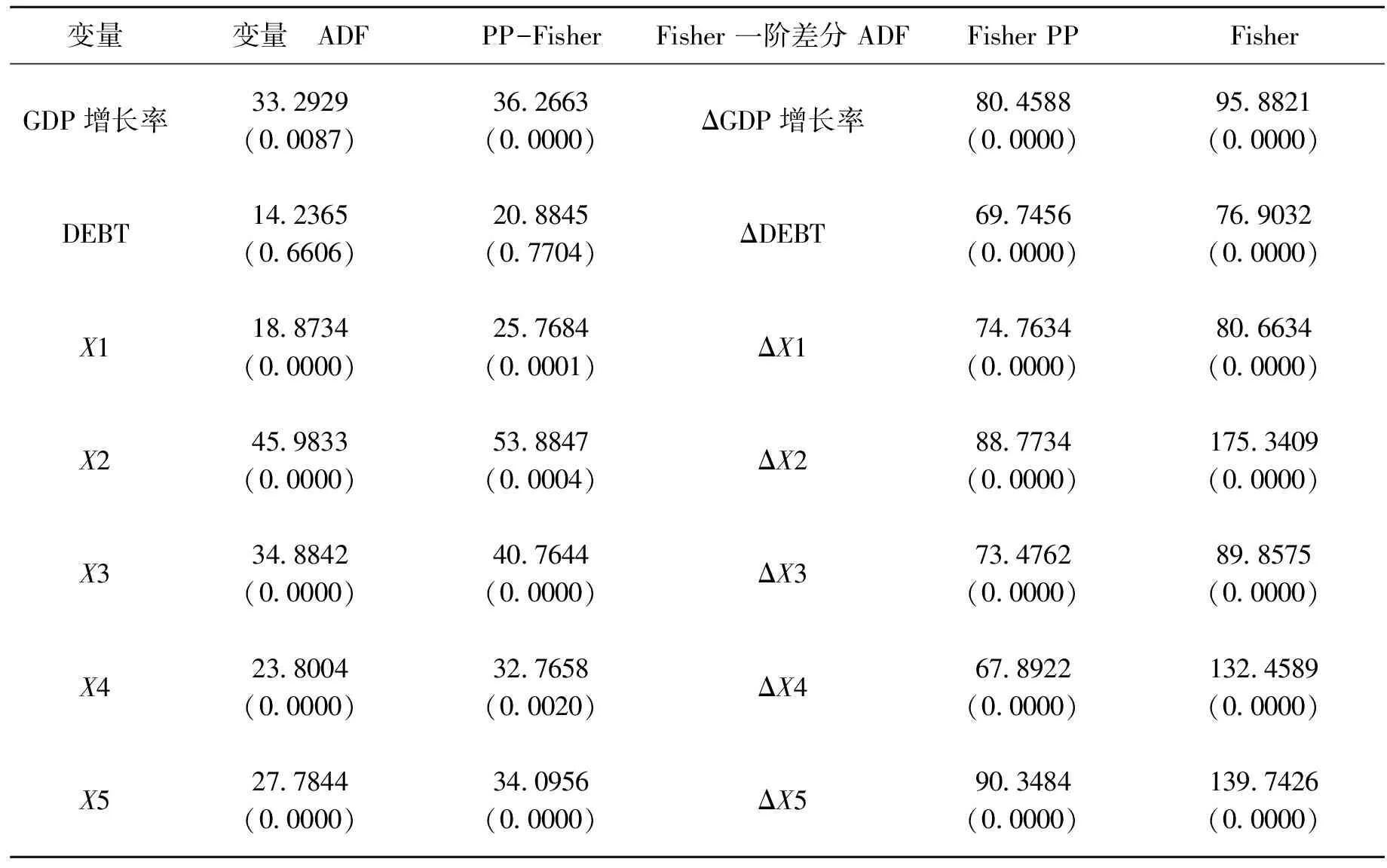
2 山东省政府债务和经济增长关系的总体分析
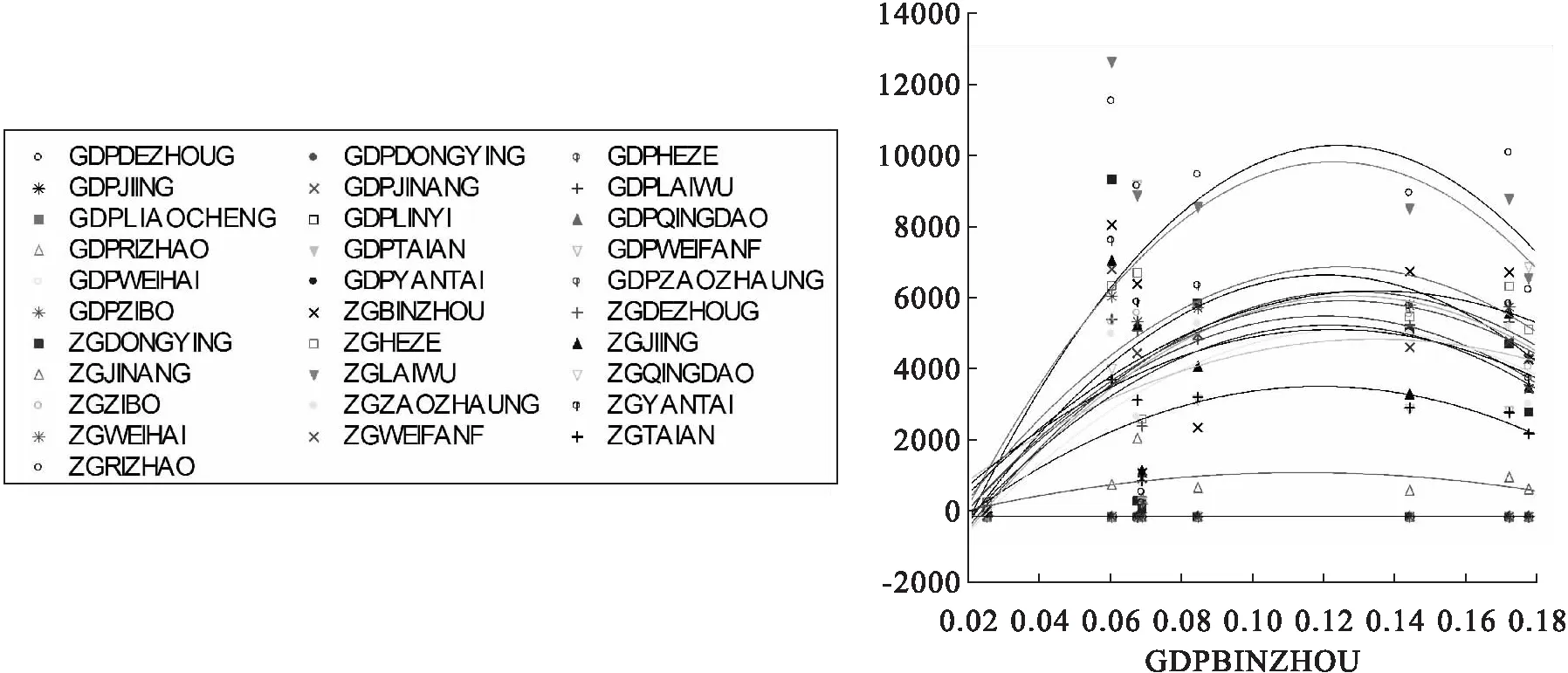
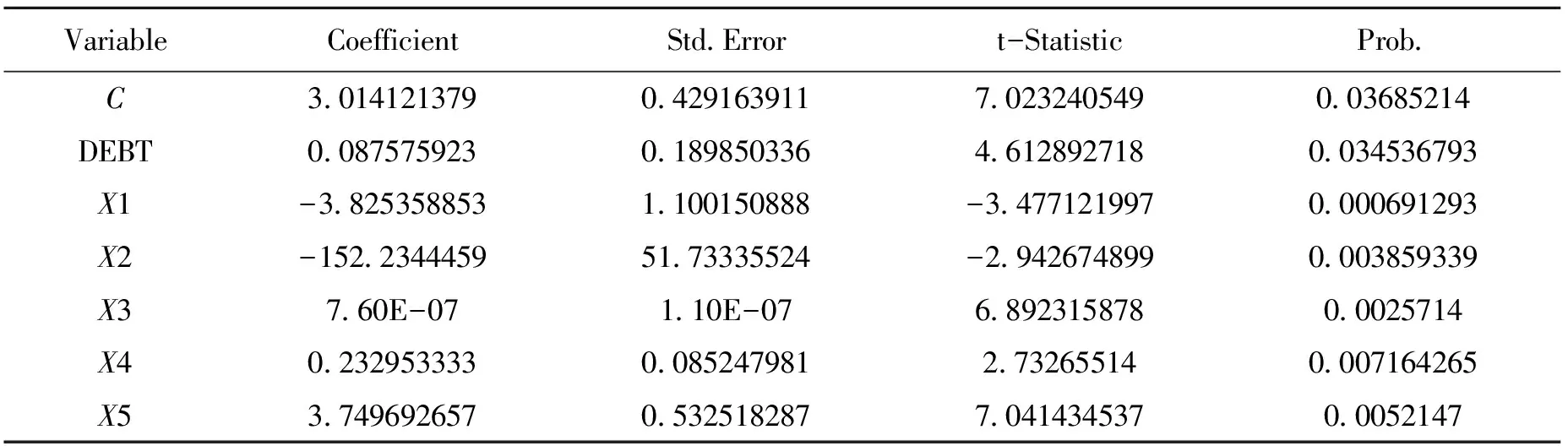
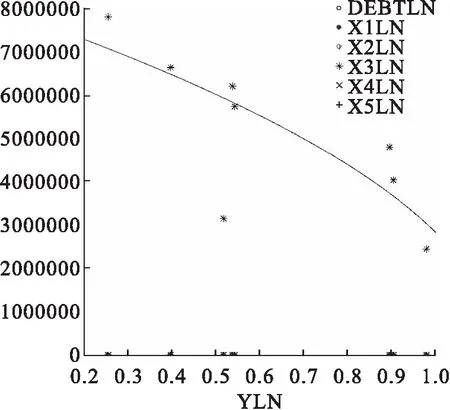
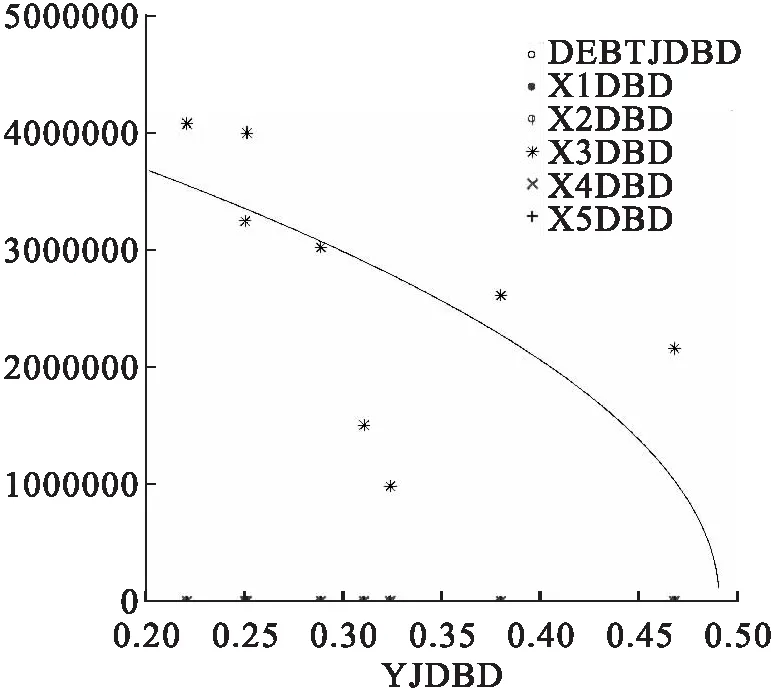
3 分区域回归分析区域政府债务和经济增长关系
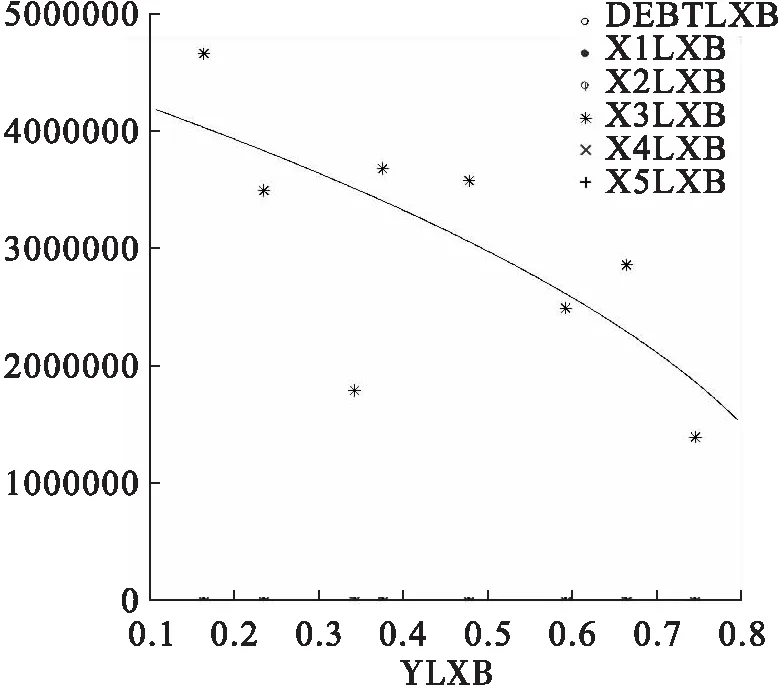

4 结论
——山东省济宁市老年大学之歌

